On se contentera de réponses courtes, sauf lorsqu'il est demandé de justifier un résultat donné. Les applications numériques seront données avec un seul chiffre significatif.

Mesurer les mouvements de la couche superficielle du Soleil, dite photosphère, permet d'avoir des informations sur la rotation de notre étoile, ses oscillations internes, et son champ magnétique. Dans la première partie, nous allons nous intéresser à un dispositif optique qui permet la mesure de ces mouvements, l'instrument MDI (Michelson Doppler Imager) embarqué à bord du satellite SOHO (Observatoire solaire et héliosphérique), lancé en 1995. La seconde partie sera consacrée à l'utilisation de ces observations pour mesurer les oscillations internes du Soleil, et à l'interprétation de celles-ci. Les différentes parties sont dans une large mesure indépendantes.

I - Principe du dispositif optique

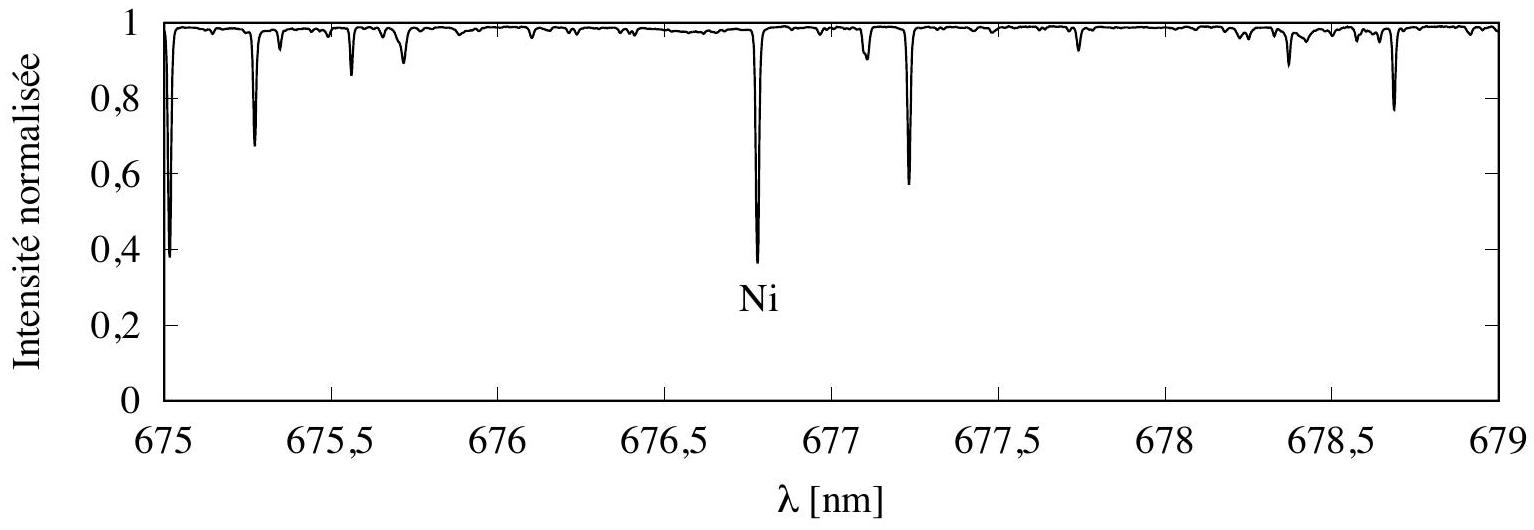
Figure 1 - Détail du spectre du rayonnement solaire autour de la raie du nickel. [Source : BASS2000 - Observatoire de Paris-Meudon - LESIA.]

Le principe est de mesurer la vitesse radiale (projection de la vitesse sur la direction d'observation) de chaque point de la photosphère. On utilise pour cela le fait que le spectre de la lumière issue du Soleil présente plusieurs creux très étroits (voir figure 1) résultant de l'absorption de la lumière par divers atomes présents dans le Soleil. Ces creux, nommés "raies", correspondent à des transitions électroniques entre deux niveaux d'un atome. Lorsque la photosphère est en mouvement, les positions observées des raies sont légèrement déplacées par effet Doppler.

Le choix technique de l'instrument MDI est d'utiliser une seule de ces raies, centrée sur la longueur d'onde

, d'une largeur de

, correspondant à une transition électronique de l'atome de nickel, et que nous désignerons par "raie du nickel". MDI mesure l'intensité lumineuse dans cinq intervalles de longueur d'onde très étroits couvrant cette raie, repérée par le symbole Ni sur la figure 1.

Interféromètres de Michelson

Le premier défi est de ne laisser passer la lumière que dans un intervalle de longueur d'onde très petit et contrôlé. Ce filtrage se décompose en plusieurs étapes. Un premier dispositif, dit filtre de Lyot, que nous n'étudierons pas, ne laisse passer la lumière que dans une bande passante de

autour de la raie du nickel. Pour affiner encore le filtrage, on utilise un dispositif
constitué de deux interféromètres de Michelson associés en série, que nous allons étudier plus en détail.

Dans quel domaine du spectre électromagnétique la raie du nickel est-elle située?
Le premier interféromètre de Michelson est équivalent à une lame d'air à faces parallèles d'épaisseur . Dessiner le schéma de l'interféromètre de Michelson, et nommer ses éléments constitutifs essentiels.
On suppose dans tout ce qui suit que les rayons frappent les miroirs de l'interféromètre sous incidence normale. Donner alors l'expression de l'ordre d'interférence en fonction de det de la longueur d'onde du rayonnement incident.
On note la valeur de pour . Calculer sa valeur approximative.
Déterminer l'expression de l'intensité à la sortie de l'interféromètre de Michelson en fonction de , en notant sa valeur maximale.
On suppose entier. Déterminer l'expression de l'intensité transmise pour une longueur d'onde , avec . Quel est l'intervalle de longueur d'onde entre deux pics d'intensité, dit intervalle spectral libre?
Calculer numériquement la valeur de cet intervalle.
L'instrument MDI comprend un second interféromètre de Michelson, équivalent à une lame d'air d'épaisseur . Quel est, pour ce second interféromètre seul, l'intervalle spectral libre?
Le deuxième interféromètre de Michelson est placé à la sortie du premier. On ne se préoccupera pas de la lumière réfléchie par le deuxième interféromètre vers le premier. Déterminer l'expression de l'intensité transmise en sortie du deuxième interféromètre, en fonction de . On notera de nouveau l'intensité maximale.

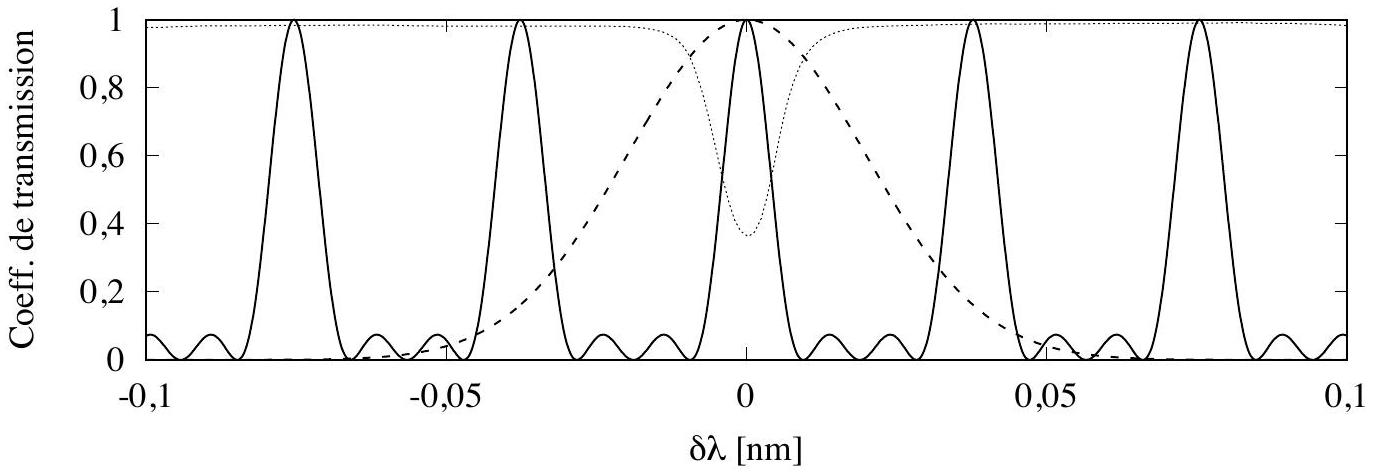
Figure 2 - Décomposition du filtrage opéré par l'instrument MDI en fonction de

. La ligne pointillée représente la raie du nickel, la ligne tiretée le coefficient de transmission du filtre de Lyot placé en entrée, et la ligne pleine le coefficient de transmission du système des deux interféromètres de Michelson qui le suit.

Vérifiez que la courbe représentée en trait plein sur la figure 2 est en accord avec le résultat de la question précédente. Vous détaillerez votre réponse et préciserez la position des points remarquables.
Quelle est l'action combinée du filtre de Lyot et des deux interféromètres de Michelson, en vous appuyant sur la figure 2?

Utilisation de la polarisation

Le second défi est de pouvoir modifier très légèrement la valeur de la longueur d'onde correspondant au pic d'intensité. On modifie pour cela les interféromètres de Michelson décrits précédemment en y ajoutant plusieurs éléments nouveaux agissant sur la polarisation de la lumière.

Dans tout ce qui suit, on ne considère, pour simplifier, qu'un seul des deux interféromètres de Michelson. On note

le plan contenant la trajectoire du rayon lumineux dans l'interféromètre. Dans le cas d'une polarisation rectiligne, on désigne par

une onde polarisée perpendiculairement à

, et par

une onde polarisée parallèlement à

. On remplace la lame séparatrice de l'interféromètre par une lame qui réfléchit totalement les ondes

, et transmet totalement les ondes

.
12. Dessiner la trajectoire du rayon lumineux dans l'interféromètre pour une onde

, puis pour une onde

. Expliquer pourquoi un tel dispositif est sans intérêt.
13. On modifie le dispositif en collant sur chacun des deux miroirs de l'interféromètre une lame quart d'onde dont la ligne neutre fait un angle

par rapport au plan

. Cette lame quart d'onde est traversée deux fois, avant et après réflexion sur le miroir, et se comporte donc comme une lame demi-onde. On rappelle que si une onde de polarisation rectiligne traverse une lame demi-onde, la polarisation en sortie est toujours rectiligne, avec une direction de polarisation symétrique de celle d'entrée par rapport à la ligne neutre. Quelle est son action sur une onde

? Sur une onde

?
14. Dessiner la trajectoire du rayon lumineux dans ce nouveau dispositif pour une onde polarisée

en entrée, puis pour une onde polarisée

en entrée. À chaque étape de la trajectoire, vous préciserez l'état de polarisation de l'onde.
15. On place devant l'entrée de l'interféromètre de Michelson un polariseur dont l'axe forme un angle de

avec le plan

. Quel est alors l'état de polarisation de l'onde à la sortie de l'interféromètre? Expliquer pourquoi on n'observe pas d'interférences avec ce dispositif.
16. On place à la sortie de l'interféromètre de Michelson une lame quart d'onde dont la ligne neutre forme un angle de

avec le plan

. On admet qu'après cette lame, la polarisation de l'onde est rectiligne et fait un angle

avec la ligne neutre de la lame, où l'expression de

a été obtenue à la question 3. Vérifier ce résultat dans le cas où

est entier.
17. On place enfin, à la suite du dispositif précédent, un polariseur linéaire. Expliquer comment, en variant l'orientation de ce polariseur, on peut obtenir le résultat cherché, et varier la longueur d'onde correspondant au pic d'intensité.

Cartographie de la vitesse de la photosphère

L'ensemble du dispositif est placé dans un télescope équivalent à une lentille mince de longueur focale . On place un capteur photographique électronique dans le plan focal. Ce capteur est formé d'un réseau carré comportant pixels, dont le pas est de . Le diamètre angulaire du Soleil vu du satellite est rad. Les dimensions du capteur lui permettent-elles d'observer l'intégralité de la photosphère solaire?
Chaque pixel du capteur mesure successivement l'intensité lumineuse autour de 5 longueurs d'onde équidistantes. On note ces intensités, par ordre croissant de . Le dispositif est calibré de telle sorte que corresponde au centre de la raie du nickel, qui est parfaitement symétrique, si la photosphère est immobile. On mesure les combinaisons suivantes :

La photosphère est en mouvement à une vitesse radiale

par rapport au satellite. Identifier, parmi les combinaisons

, laquelle est susceptible d'être proportionnelle à

.
20. La vitesse de la photosphère vient en premier lieu de la rotation du Soleil, dont l'axe de rotation est perpendiculaire au plan de l'orbite de la Terre, dans lequel se trouve également le satellite SOHO . On choisit un système de coordonnées cartésiennes (

) dont l'origine

est le centre du Soleil, l'axe

est l'axe de rotation du Soleil, et l'axe

la droite joignant le centre du Soleil au satellite. Exprimer la vitesse radiale d'un point de la photosphère en fonction de la vitesse angulaire

du Soleil et des coordonnées, en précisant la convention choisie pour le sens de rotation.
21. Cette vitesse radiale

atteint la valeur

près de l'équateur du Soleil. Que vaut alors le déplacement

de la raie du nickel résultant de l'effet Doppler? On rappelle que la vitesse de la lumière dans le vide vaut

. Comment

se compare-t-il à la largeur de la raie? Commenter.

II - Éléments de physique des oscillations solaires

Outre son mouvement de rotation global, le Soleil présente des mouvements internes de faible amplitude qui peuvent être modélisés comme des ondes acoustiques, à l'étude desquelles cette deuxième partie est consacrée. On effectuera d'abord une modélisation dans laquelle la vitesse du son est uniforme dans une couche d'épaisseur

au-dessous de la surface du Soleil. Bien que non réaliste, cette modélisation permettra de comprendre les bases du phénomène étudié. Dans un second temps, on étudiera le cas plus réaliste où la vitesse du son dépend de la distance au centre du Soleil. On négligera, dans toute cette partie, les effets liés à la rotation du Soleil.

Modèle de fluide uniforme

Soit un fluide homogène au repos, isolé, de pression uniforme , dans lequel se propage une onde acoustique dans la direction . On décompose la pression en , où est une surpression de faible amplitude. Établir l'équation de propagation de la surpression dans l'approximation acoustique. Dans cette partie, on notera la vitesse du son dans le fluide.
Rappelez, sans démonstration, la généralisation de cette équation à trois dimensions.

Nous allons étudier des mouvements internes cantonnés aux couches supérieures du Soleil. Nous supposons plus précisément que l'onde acoustique est cantonnée à une couche d'épaisseur

, beaucoup plus petite que le rayon

du Soleil. Par ailleurs, afin d'éviter les complexités liées à la géométrie sphérique, nous nous limitons dans tout ce qui suit à une géométrie plus simple. Nous étudions la propagation dans une bande étroite de largeur constante (très petite devant

), faisant tout le tour du Soleil en suivant l'équateur. On note

l'abscisse curviligne le long de cette bande et

la coordonnée verticale orientée vers le haut, qui varie entre

et 0 , où

définit la surface du Soleil. On cherche des modes d'oscillation de la forme

où nous avons introduit la représentation complexe, et

désigne la partie réelle du complexe

.
24. Les quantités physiques doivent être périodiques en

, de période

, correspondant à un tour complet autour du Soleil. Quelles sont alors les valeurs possibles de

? On les repérera par un entier

.
25. Les données du capteur photographique de l'instrument MDI sont traitées par ordinateur. Par analyse de Fourier, on parvient à séparer les contributions des différentes valeurs de

. On
parvient à reconstruire les modes jusqu'à environ

. Expliquez pourquoi ce nombre est plausible, au vu des caractéristiques techniques du capteur indiquées question 18.
26. On néglige la gravité, de telle sorte que l'équation de propagation de la surpression déterminée plus haut s'applique. On traite les coordonnées

comme des coordonnées cartésiennes, ce qui est justifié par l'hypothèse d'ondes peu profondes. Écrire l'équation différentielle satisfaite par

.
27. On postule les conditions aux limites

. Interpréter physiquement ces conditions aux limites.
28. Résoudre l'équation différentielle avec ces conditions aux limites. En déduire les pulsations des modes propres pour

donné, que l'on classera par ordre croissant en les repérant par un entier

positif ou nul et qu'on notera

.
29. Représenter sur un même graphique la variation de

en fonction de

dans ce modèle.
30. Montrer que la famille de courbes

, avec

, se réduit à une courbe unique si on choisit d'exprimer

en fonction de

. Donner l'expression de

en fonction de

et tracer

Modèle de fluide stratifié

La vitesse du son croît avec la température qui, dans le Soleil, augmente lorsqu'on se rapproche du centre. Nous affinons maintenant la modélisation en prenant en compte cette variation. Nous notons

la vitesse du son à l'altitude

, avec

, qui décroît en fonction de

. On traite la propagation de l'onde dans l'approximation de "l'acoustique géométrique", qui est analogue à l'approximation de l'optique géométrique pour la propagation des ondes électromagnétiques. Dans cette approximation, l'onde acoustique est représentée par un rayon. On note

le vecteur d'onde en un point donné du rayon. On admet que

est constant le long du rayon.
31. Écrire la relation de dispersion reliant

, où nous notons

la composante verticale du vecteur d'onde à l'altitude

.
32. On note

l'inclinaison du rayon par rapport à l'axe

. Exprimer sin

en fonction de

. Quel est l'analogue de ce résultat en optique géométrique?
33. On suppose que la vitesse du son croît indéfiniment lorsque

diminue. Montrer que le rayon ne peut descendre en dessous d'une altitude

, et écrire la relation entre

.
34. On suppose que le rayon se réfléchit lorsqu'il atteint la surface du Soleil. Dessiner alors l'allure de la trajectoire d'un rayon partant d'un point quelconque de la surface du Soleil.
35. Dessiner, pour comparaison, l'allure de la trajectoire d'un rayon pour le modèle de fluide uniforme étudié plus haut.
36. On admet que les modes propres sont déterminés par la condition

où

est un entier positif ou nul, et

une constante indépendante de

. Montrer que pour un fluide uniforme, cette condition est équivalente à celle obtenue à la question

pour une valeur de

qu'on précisera.

La figure 3 représente les mesures de l'instrument MDI, où on a porté en abscisse

et en ordonnée

. La constante

a été ajustée à la valeur

qui permet que les points correspondant à des valeurs de

différentes se retrouvent approximativement sur la même courbe.

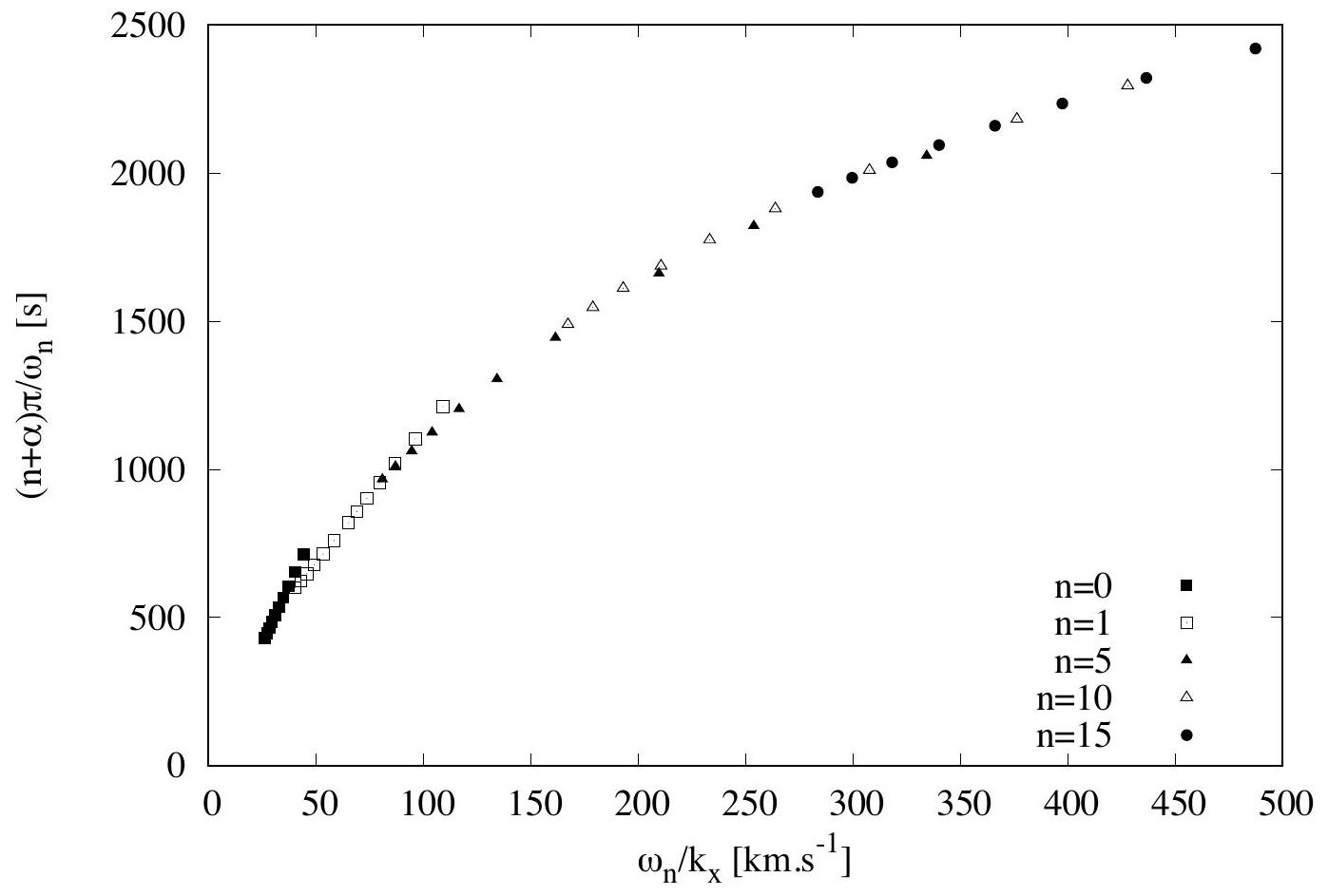
Figure 3 - Résultats des mesures de l'instrument MDI après 144 jours d'observation, pour quelques valeurs de

et de

. [Données fournies par Jørgen Christensen-Dalsgaard.]

À quelle condition deux ondes, caractérisées par leurs pulsations et , et leurs nombres d'onde horizontaux et , correspondent-elles à des rayons identiques?
Montrer que l'équation (3) implique que tous les points de la figure 3 sont sur une courbe unique.
À quelles conditions sur et l'approximation géométrique, qui conduit à l'équation (3), est-elle pleinement justifiée?