L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
On se contentera, pour les applications numériques, d'un ou deux chiffres significatifs.

Objectif Lune

Ce problème traite de la télémétrie laser appliquée à la mesure précise de la distance séparant la Terre de la Lune. Il se compose d'un texte de 3 pages, de deux figures montrant des données expérimentales et de 30 questions d'analyse et de compréhension auxquelles le candidat doit répondre. Ces questions sont regroupées en six courtes parties indépendantes.

Commencez par lire attentivement le texte intitulé "La télémétrie laser-Lune". Cela devrait vous prendre entre 20 et 30 minutes.

Puis répondez aux questions de la partie intitulée "Analyse de l'article". Elles ne sont pas forcément ordonnées par difficulté croissante et certaines d'entre elles ont une formulation ouverte. Dans ce cas, toutes vos initiatives de résolution sont bienvenues à condition de justifier et de détailler systématiquement votre démarche. Si nécessaire, vous citerez précisément la partie du texte qui appuie votre raisonnement (les lignes sont numérotées de 1 à 236 à cet effet). Les hypothèses des modélisations doivent être clairement précisées et toutes les approximations doivent être explicitées et justifiées. Les calculs devront être menés sous forme littérale, avec pour objectif final d'obtenir une valeur numérique.

Données utiles pour l'analyse du texte

Accélération de la pesanteur		Rayon de la Terre
Contante des gaz parfaits		Masse de la Terre
Masse molaire de l'air		Rayon de la Lune
Distance Terre-Soleil		Masse de la Lune

Un photon dont la longueur d'onde est de

a une énergie de

.
Une année dure

secondes.
Un angle d'une seconde d'arc correspond à

radian.
Le moment d'inertie d'une boule homogène de masse

et de rayon

par rapport à un axe passant par son centre est donné par


0,819	0,766	0,707	0,643	0,574	0,500
0,809	0,755	0,695	0,629	0,559	0,485
0,799	0,743	0,682	0,616	0,545	0,469
0,788	0,731	0,669	0,602	0,530	0,454
0,777	0,719	0,656	0,588	0,515	0,438

Table 1: Extrait d'une table trigonométrique par degré, à 0,001 près.

La télémétrie laser-Lune *

Abstract

Résumé La télémétrie laser permet de déterminer avec précision de grandes distances. La cible la plus éloignée jamais atteinte par cette méthode est notre satellite naturel, la Lune. Principe simple et mise en œuvre délicate caractérisent cette technique, utilisée avec succès depuis l'observatoire de la Côte d'Azur. Passée en 10 ans d'une trentaine de centimètres à moins de trois, la précision des mesures devrait atteindre quelques millimètres d'ici 1995. Cela améliorera notre connaissance de la dynamique du système Terre-Lune, de la rotation de la Terre, de l'intérieur de la Lune et permettra de tester la théorie de la gravitation.

1 Mesurer une distance par une durée

Le principe de la télémétrie laser-Lune est simple. Un télescope envoie une impulsion lumineuse vers un réflecteur posé sur la surface lu- naire. Une partie de la lumière émise est renvoyée et va, après environ deux secondes et demie, être reçue par le même télescope. Il suffit de dater l'instant de départ de l'impulsion et celui du retour de l'écho pour connaître la durée de tra- jet. En multipliant cette durée par la vitesse de la lumière, on obtient la longueur du trajet parcouru, égale au double de la distance de notre télescope à la Lune, ou plus précisément au réflecteur visé.
un seul fonctionne encore. Quatre réflecteurs sont donc aujourd'hui disponibles sur la Lune.

À quoi ressemblent ces cataphotes ? Ce sont des coins de cube qui ont la propriété essentielle de renvoyer la lumière dans la direction d'où elle est arrivée grâce aux réflexions successives sur trois plans réfléchissants perpendiculaires deux à deux. On est ainsi assuré de recevoir des échos de la lumière envoyée, quelles que soient les positions respectives du télescope, qui suit le mouvement de la Terre en rotation sur elle-même et autour du Soleil, et du réflecteur qui se déplace au gré du mouvement de la Lune sur son axe et autour de la Terre.

Figure 1: Le réflecteur (

cataphotes) déposé sur la Lune par la mission Apollo 15.

2 La chasse aux photons

La télémétrie laser-Lune est une technique assez difficile à mettre en œuvre. L'intérêt du laser est qu'il permet d'envoyer de l'ordre de

photons en peu de temps. Dans les meilleures conditions, on ne détecte qu'un photon en écho tous les cent tirs! Sachant que les lasers actuels permettent une cadence de dix tirs par seconde, il faut donc attendre une dizaine de minutes pour détecter une soixantaine de photons.

Sans précautions, ces photons sont noyés dans ceux du ciel si l'on travaille de jour, ceux de la Lune si le réflecteur visé est dans le croissant éclairé, et aussi ceux du détecteur, imparfait. Il faut donc identifier les bons photons - ceux des échos - des mauvais - le bruit. Pour cela, commençons par isoler une zone de quelques secondes d'arc (une dizaine de kilomètres sur la Lune) autour du réflecteur visé. Ensuite, on ne considère que les photons de la bonne couleur. Le laser étant stabilisé en température, sa longueur d'onde est bien définie. Un filtre ayant une bande passante étroite - moins de

- permet de ne détecter que les photons qui ont la bonne longueur d'onde. Malgré ces précautions, on détecterait plus d'un million de photons par seconde si les conditions sont défavorables! Il faut donc réaliser un ultime filtrage, temporel celui-

3 Pour quelles applications?

Pour pouvoir calculer la durée du trajet séparant le télescope du panneau de réflecteurs, il faut modéliser les différents mouvements du système Terre-Lune.

Commençons par le réflecteur dont le déplacement le plus important est celui dû au mouvement de la Lune autour de la Terre. La télémétrie laser-Lune a permis un bond de trois ordres de grandeur dans la précision de détermination des paramètres orbitaux de la Lune. Il en est de même pour sa rotation, synchronisée avec sa révolution (c'est pour cela que la Lune nous montre toujours la même face). En fait, la face visible de la Lune oscille autour d'une position moyenne à cause de l'influence du Soleil et de l'interaction entre la Terre et son satellite, qui ne sont ni sphériques, ni homogènes, ni rigides... La confrontation entre modèles et observations permet notamment d'étudier l'intérieur de la Lune, car la rotation d'un corps sur lui-même dépend de sa structure interne (faites tourner un œuf cru et un œuf dur pour vous en convaincre !) et de sa répartition de
ci. Sachant quand l'impulsion laser a été émise, le calculateur qui gère l'expérience en temps réel estime le moment d'arrivée de l'écho grâce à notre bonne connaissance du mouvement de la Lune. Et plutôt que de regarder en permanence, le détecteur électronique (un photomultiplicateur ou une photodiode) ne va s'ouvrir qu'un peu avant le moment prédit, pour se fermer un peu après. Ce très petit intervalle de détection, de l'ordre de cent milliardièmes de seconde, élimine la plus grande partie du bruit. Un traitement statistique des photons reçus permettra enfin de valider la présence de l'écho.

Il est impossible de savoir si le photon de retour que l'on détecte vient du début ou de la fin de l'impulsion laser émise. C'est là l'incertitude fondamentale de la télémétrie laser quand on ne reçoit en écho qu'au plus un photon par tir. Plus l'impulsion émise est courte, plus cette incertitude est faible, mais moins on émet de photons car il est difficile d'émettre beaucoup d'énergie en un temps très faible. La durée de l'impulsion correspond à une incertitude tir à tir d'une dizaine de centimètres sur la mesure de distance, incertitude ramenée à un ou deux centimètres en accumulant les échos sur une dizaine de minutes.
masse. L'étude de l'évolution passée ou future de l'orbite lunaire nécessite aussi la télémétrie laser-Lune, seule méthode capable de fournir une mesure de la décélération séculaire de la Lune et un instantané précis des mouvements actuels.

Passons maintenant au mouvement de la station. Elle se trouve sur la Terre qui tourne sur elle-même en 23 heures et 56 minutes. Cette rotation n'est pas parfaitement régulière car la direction de son axe et sa vitesse fluctuent. Il faut donc modéliser précisément cette rotation à laquelle les mesures sont très sensibles. D'autres techniques contribuent à l'étude de la rotation de la Terre (interférométrie à grande base, télémétrie laser sur satellites...), mais le laser-Lune permet une prédiction rapide, fondée sur des observations récentes de la rotation de la Terre.

Terre et Lune étant en orbite autour du Soleil, la télémétrie laser-Lune contribue à l'élaboration des éphémérides du système solaire. Ainsi, elle permet de mesurer l'angle entre l'écliptique (le plan contenant l'orbite moyenne de la Terre) et le plan équatorial de la Terre, élément clé de la navi-
gation spatiale. Elle permet aussi de déterminer le rapport des masses de la Terre et de la Lune.

La télémétrie laser-Lune permet enfin de tester la théorie de la gravitation d'Einstein, la relativité générale. Terre et Lune ont des masses très importantes et des vitesses que l'on ne peut négliger par rapport à la vitesse de la lumière.

Appendices

A Vous avez dit distance ?

La durée du trajet aller-retour n'est pas immédiatement convertible en distance car entre l'émission de l'impulsion par le télescope et son arrivée sur la Lune, cette dernière s'est déplacée et le réflecteur avec elle. Entraîné par la rotation de la Terre, le télescope s'est aussi déplacé entre le départ et le retour de l'impulsion. De plus, l'infime ralentissement de la lumière dans l'atmosphère se traduit par un allongement de la durée du trajet. Équivalent à plusieurs mètres sur la distance, cet écart est d'autant plus grand que l'impulsion laser traverse une couche d'atmosphère plus épaisse, donc que la Lune est basse sur l'horizon. Il faut aussi modéliser l'atmosphère le long du trajet de la lumière à partir des paramètres météorologiques mesurés à la station. L'incertitude de cette correction est de quelques millimètres pour une hauteur de

au-dessus de l'horizon, mais peut atteindre deux centimètres si la Lune n'est qu'à

. Enfin, selon la relativité générale, la durée de propagation de la lumière dans le potentiel gravitationnel d'un objet massif (pour nous, le Soleil essentiellement) est plus longue que celle en l'absence de cet objet. Dans le cas d'un trajet Terre-Lune, ce retard est équivalent à allonger leur distance de près d'une dizaine de mètres !

B Quelques nombres

Le télescope a un diamètre de 1,5 mètre et sa focale est de 30 mètres. À la sortie du télescope, le faisceau a un angle d'ouverture de 1 seconde d'arc mais l'agitation de l'atmosphère augmente cette valeur qui devient de l'ordre de 5 secondes d'arc. Le laser utilisé envoie des impulsions de 600 mJ à une longueur d'onde

ou de 300 mJ à tation propre.

La précision relative des mesures de distance, quelques

, rend indispensable la prise en compte de la relativité et permet de tester la validité de ses principes. C'est ainsi que le principe d'équivalence

se trouve vérifié avec une très bonne précision pour des corps comme la Terre et la Lune (voir l'appendice C ).

. La durée d'une impulsion est de 400 ps et la cadence de tir est de 10 Hz . Le réflecteur de la mission Apollo 15 est composé de 300 cataphotes ayant chacun une ouverture circulaire de

de diamètre.

C Laser-Lune et relativité

En dehors de l'amélioration de notre connaissance des mouvements de la Lune offerte par les observations laser-Lune, la plus importante application en physique fondamentale a trait à la gravitation. Vérifier que la constante de la gravitation

ne variait pas était l'un des buts annoncés. Une diminution de

au cours du temps se traduirait par une décroissance de la vitesse angulaire orbitale de la Lune, une décélération séculaire donc. Or, les interactions de marée entre la Terre et la Lune sont responsables d'une décélération séculaire de la Lune (le laser-Lune donne -24 secondes d'arc par siècle au carré) qui doit être précisément modélisée pour isoler la contribution d'une éventuelle variation de

. La limite actuelle est

an . Une autre application de type relativiste a été suggérée par K. Nordtvedt en 1968 : si la Terre et la Lune ne répondaient pas de la même façon au champ de gravitation du Soleil, violant ainsi le principe d'équivalence de la relativité générale, l'orbite de la Lune autour de la Terre se trouverait allongée le long de l'axe Terre-Soleil. En 1976, deux équipes américaines ont montré qu'aucun effet Nordtvedt n'était mesurable, conduisant à une vérification du principe d'équivalence à

près. Le laser-Lune est à l'heure actuelle le meilleur test du principe d'équivalence pour des corps dont la cohésion est assurée par leur gravi-

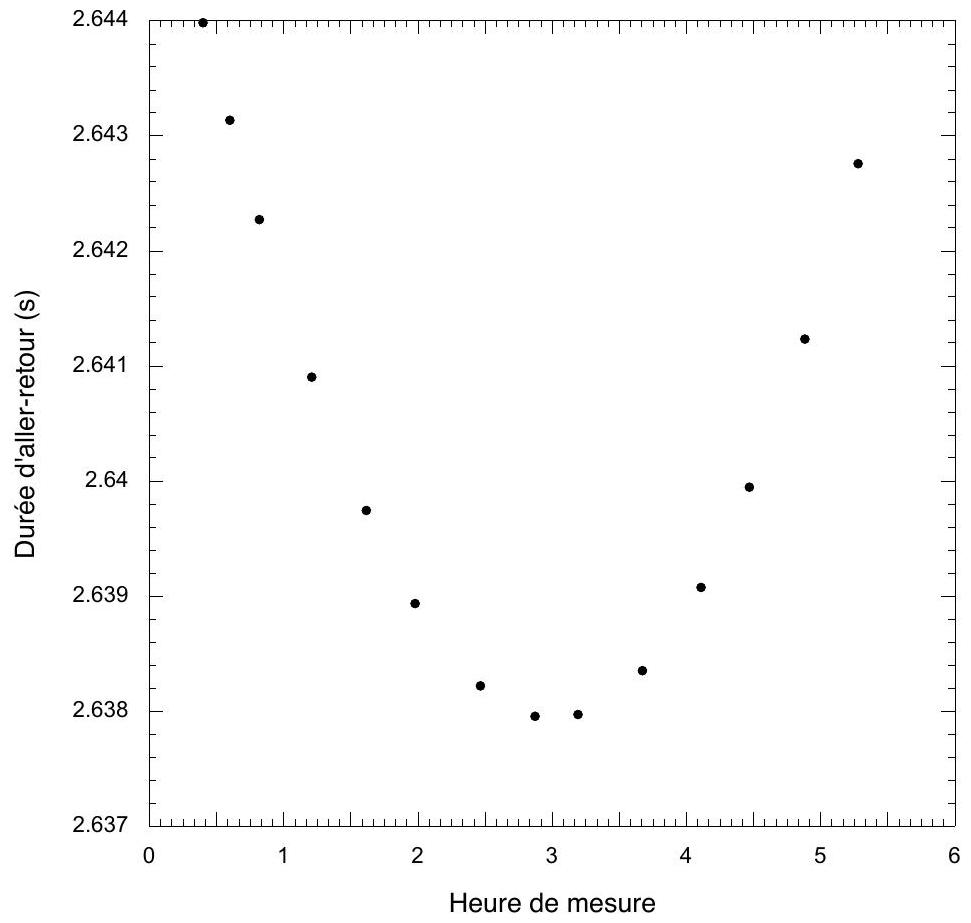
Figure 2: Observations menées dans la nuit du 25 mars 2000 , donnant la durée d'aller-retour de la lumière entre l'observatoire et la Lune en fonction de l'heure. Sur l'axe des abscisses, le temps est compté en heures et l'origine correspond à minuit.

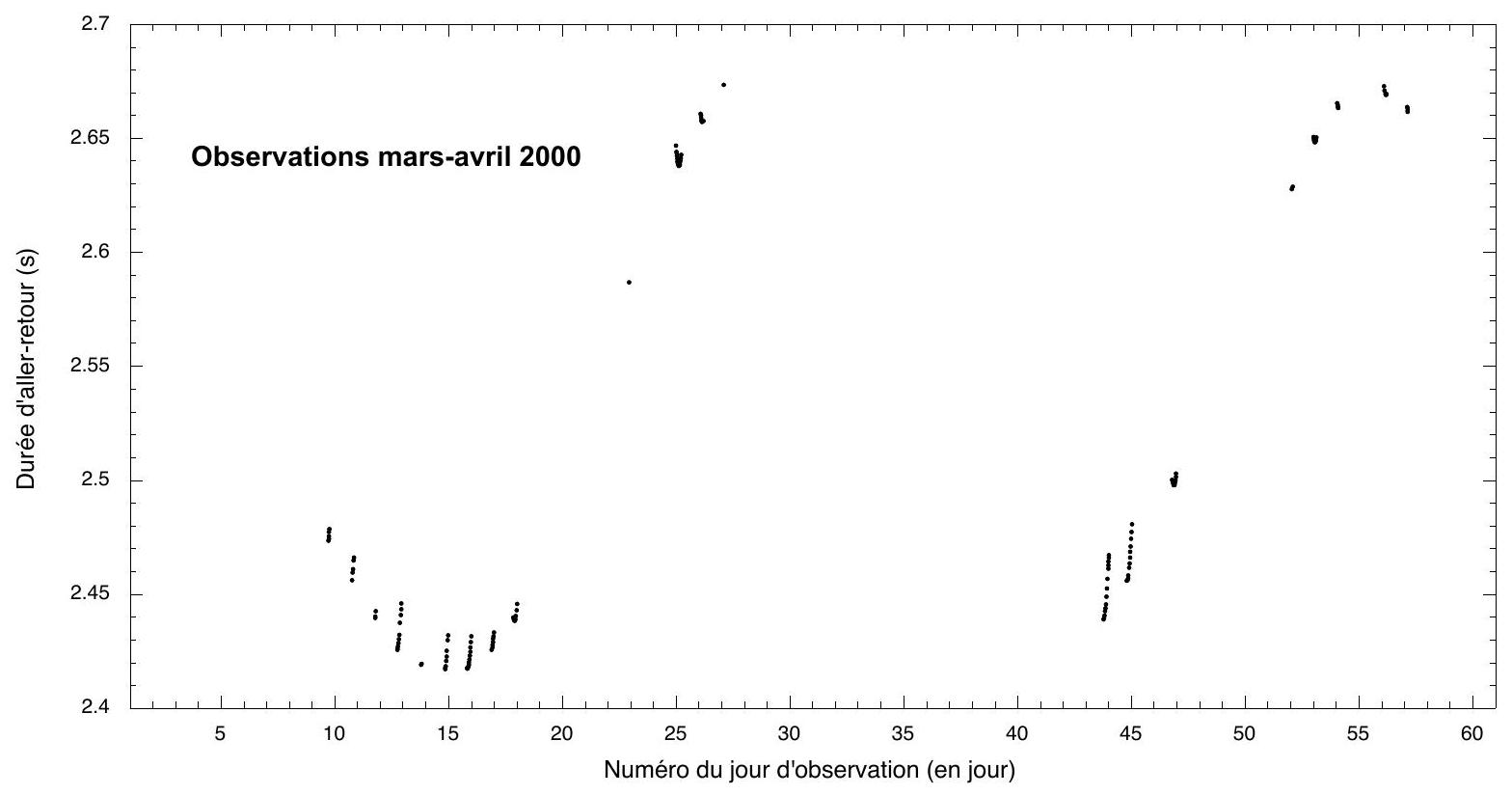
Figure 3: Observations menées aux mois de mars et d'avril 2000, donnant la durée d'aller-retour de la lumière entre l'observatoire et la Lune en fonction du temps. L'axe des abscisses est gradué avec un pas de 1 jour à partir de la graduation 1 qui correspond au

mars 2000.

Analyse de l'article

Estimez la distance séparant la Terre de la Lune grâce aux données du début du texte.

I - Traversée de l'atmosphère

L'atmosphère terrestre est supposée en équilibre hydrostatique dans un champ de pesanteur uniforme. Elle est assimilée à un gaz parfait de masse molaire

, sans autre hypothèse particulière. Sa pression

, sa température

, sa masse volumique

et son indice optique

varient avec l'altitude

. On suppose que

est proportionnel à

.
2. Pour un tir vertical, quelle correction

faut-il apporter à la mesure de la distance

à cause de l'atmosphère? Vous l'exprimerez sous forme d'une intégrale sur l'épaisseur de l'atmosphère.
3. Exprimez

en fonction de

, indice optique au sol (

), et d'une longueur

fonction de la température au sol

. Quelle est l'interprétation physique de

?
4. Sachant que

et que

, calculez

. Comparez cette dernière valeur à celle indiquée dans le texte (ligne 176).
5. Comment l'expression de

obtenue à la question 3 est-elle modifiée pour un tir incliné de l'angle

par rapport à l'horizontale ?

II - Trajet Terre - Lune

D'après le texte (lignes 186-192) la durée du trajet Terre-Lune est affectée par la présence du Soleil. On suppose que la variation relative de la durée de ce trajet est proportionnelle au potentiel gravitationnel du Soleil et fait aussi intervenir , la vitesse de la lumière dans le vide. Par un raisonnement dimensionnel, exprimez la correction à apporter à la distance Terre-Lune résultant de cet effet. Dans votre résultat final, faites apparaître la vitesse de révolution de la Terre autour du Soleil.
Estimez numériquement la valeur de . Calculez la correction de distance due à la présence du Soleil et comparez-la à ce qu'indique le texte (ligne 192).

III - L'écho lumineux

Le faisceau lumineux émis depuis la Terre est un cône dont l'angle d'ouverture est noté

. On note

la surface du miroir du télescope et

la surface du réflecteur placé sur la Lune. On supposera que tous les miroirs sont parfaits. Le laser vert utilisé a une longueur d'onde

.
8. Calculez le nombre

de photons émis par une impulsion laser et vérifiez que votre valeur est cohérente avec celle indiquée dans le texte (ligne 52).
9. L'ouverture du faisceau à la sortie du télescope (ligne 196) est-elle due à la seule diffraction ?
10. En tenant compte de l'agitation atmosphérique (ligne 198), quelle est la fraction d'énergie lumineuse reçue par le réflecteur lunaire à chaque impulsion laser ?
11. Expliquez pourquoi les cataphotes ont la propriété de renvoyer la lumière dans la direction d'où elle est arrivée (lignes 37-42).
12. Montrez que tous les rayons lumineux réfléchis sur un même cataphote parcourent exactement le même chemin optique entre l'émission et la réception.
13. Estimez l'angle d'ouverture

du faisceau réfléchi par un cataphote dû à la diffraction.
14. Estimez le rapport entre l'énergie reçue par le télescope et celle réfléchie par les cataphotes.
15. En déduire la valeur du rapport

entre l'énergie reçue par le télescope et celle qu'il a émise.
16. Combien de photons récupère-t-on après chaque tir? Quelles raisons peut-on invoquer pour rendre compte de l'écart entre cette valeur et celle du texte (lignes

) ?
17. Expliquez pourquoi l'incertitude de mesure est liée à la durée de l'impulsion. En quoi l'accumulation de tirs permet-elle de réduire cette incertitude (lignes

) ?

IV - Analyse de la figure 2

Pour simplifier l'analyse, on suppose que l'orbite de la Lune est contenue dans le plan de l'équateur terrestre et que le réflecteur est au centre de la face visible de la Lune. On suppose aussi que la Lune tourne autour de la Terre dans le même sens que la Terre autour d'elle-même. On note

la latitude de l'observatoire où se trouve le télescope.
18. Les observations du 25 mars 2000 ont-elles été menées autour du premier quartier lunaire, de la pleine Lune ou du dernier quartier lunaire ?
19. Quelle est la principale cause de la variation de la durée aller-retour

représentée sur la figure 2 ? À quel instant

la Lune est-elle au plus haut dans le ciel de l'observatoire ?
20. Modélisez la variation temporelle de

autour de

. Dans un cadre que vous détaillerez, montrez que

s'écrit comme un polynôme du second degré en

.
21. Estimez la latitude de l'observatoire grâce à la figure 2 et à la table 1. Commentez.

V - Analyse de la figure 3

Dans cette analyse, on considère que l'orbite de la Lune est une ellipse d'équation polaire

, où

est la distance Terre-Lune et

l'angle repérant la direction de la Lune dans le plan de son orbite. Le paramètre

et l'excentricité

sont des constantes.
22. Quel est le cadre d'hypothèses qui permet d'obtenir cette orbite?
23. Quelle est la cause principale des variations de la durée d'aller-retour représentée figure 3 ?
24. Grâce à la figure 3, estimez la période de révolution

de la Lune ainsi que le demi-grand axe

et l'excentricité

de son orbite.
25. Quelles explications peut-on donner à l'absence d'observations entre les jours 27 et 43 ?

VI - Tests de physique

On suppose que la constante de gravitation varie lentement au cours du temps (lignes 211 - 216) et on en étudie les conséquences sur l'orbite de la Lune. Quelle quantité reste conservée ?
On suppose que l'orbite de la Lune est approximativement circulaire. Expliquez pourquoi une diminution de se traduit par un ralentissement de la vitesse angulaire de la Lune. Quelle est la variation relative de la vitesse angulaire si celle de est de ?
est maintenant supposée constante. Montrez qu'à la décélération séculaire (diminution de la vitesse angulaire) de -24 secondes d'arc par siècle au carré (ligne 219) est associé un éloignement de la Lune au rythme de quelques centimètres par an.
On s'intéresse maintenant à l'influence de la décélération séculaire de la Lune sur la rotation propre de la Terre. Expliquez pourquoi le moment cinétique total du couple Terre-Lune est conservé. Montrez que l'on peut négliger la contribution due à la rotation de la Lune sur elle-même.
Montrez que la décélération séculaire de la Lune modifie la période de rotation de la Terre sur elle-même. S'agit-il d'une augmentation ou d'une diminution?

*Texte extrait et adapté d'un article publié dans la revue Images de la physique en 1992.
Le principe d'équivalence énonce l'égalité de la masse gravitationnelle et de la masse inertielle de tous les corps. Rappelons qu'on appelle masse inertielle d'un corps celle qui intervient dans la relation fondamentale de la dynamique, c'est-àdire le rapport de proportionnalité entre les forces appliquées à ce corps et son accélération. La masse gravitationnelle d'un corps est la masse qui intervient dans l'expression de la force de gravitation qu'il subit.