Version interactive avec LaTeX compilé
ÉCOLE POLYTECHNIQUE
ÉCOLE SUPÉRIEURE DE PHYSIQUE ET DE CHIMIE INDUSTRIELLES
CONCOURS D'ADMISSION 2005
DEUXIÈME COMPOSITION DE PHYSIQUE
(Durée : 4 heures)
L'utilisation des calculatrices est autorisée pour cette épreuve.
Générateurs et pompes électromagnétiques à métal liquide
Ce problème se propose d'étudier le mouvement d'un fluide homogène, incompressible et conducteur, soumis à un champ électrique et champ magnétique croisés, et d'en tirer des conclusions quant à d'éventuelles applications industrielles, tout particulièrement pour la circulation de métaux liquides.
Toute l'étude est effectuée dans le référentiel du laboratoire, supposé galiléen.
On désigne par
Formule du double produit vectoriel :
Permittivité du vide :
Formule du double produit vectoriel :
Permittivité du vide :
I. Étude préliminaire
Dans un plan horizontal, un circuit électrique rectangulaire est constitué de deux rails conducteurs, fixes, parallèles, distants de
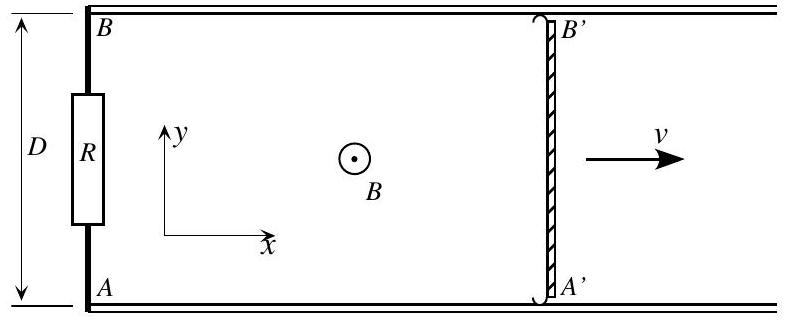
Figure 1
Le conducteur
- Montrer que ce système est un générateur électrique; calculer la f.é.m correspondante et l'intensité qui traverse le circuit orienté.
En déduire la d.d.p.
2. Le courant est dû à un mouvement d'électrons; préciser l'origine de la force qui les met en mouvement et en donner l'expression à l'aide de
3. Soit
4. Application numérique. On donne
2. Le courant est dû à un mouvement d'électrons; préciser l'origine de la force qui les met en mouvement et en donner l'expression à l'aide de
3. Soit
4. Application numérique. On donne
II. Écoulement d'un fluide conducteur
On étudie dorénavant l'écoulement d'un fluide conducteur et incompressible, de masse volumique
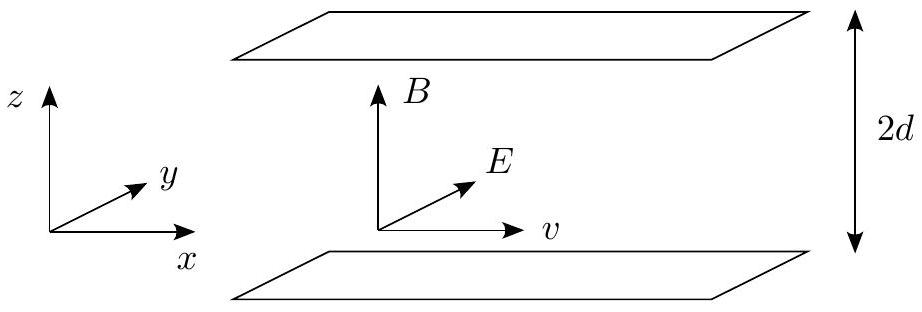
Figure 2
1. Équation du mouvement
a) Donner l'expression de la densité volumique des forces de pression
b) Soit
c) Le fluide est localement neutre. Soit
d) Écrire l'équation du mouvement du fluide. En déduire que la pression est indépendante de
b) Soit
c) Le fluide est localement neutre. Soit
d) Écrire l'équation du mouvement du fluide. En déduire que la pression est indépendante de
2. Écoulement entre deux plans parallèles
Le fluide est canalisé par deux plans horizontaux d'équations
On considère un écoulement stationnaire.
a) Écrire l'équation différentielle reliant
b) Résoudre l'équation différentielle à laquelle satisfait
c) Déterminer la vitesse moyenne du fluide
d) Que devient, pour
e) Pour
f) Application numérique. Le fluide est du sodium liquide avec les propriétés suivantes :
a) Écrire l'équation différentielle reliant
b) Résoudre l'équation différentielle à laquelle satisfait
c) Déterminer la vitesse moyenne du fluide
d) Que devient, pour
e) Pour
f) Application numérique. Le fluide est du sodium liquide avec les propriétés suivantes :
Viscosité dynamique
Conductivité
Conductivité
Calculer
III. Exemple d'application
On étudie le système schématisé figure 3 ; le sodium liquide se déplace dans un conduit cylindrique de longueur
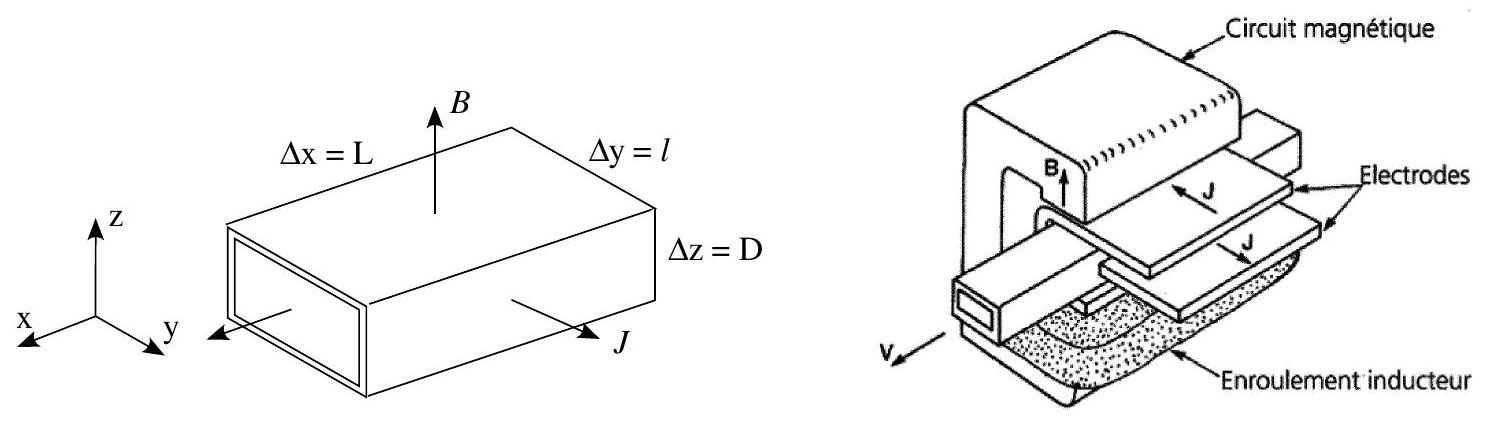
Figure 3
1.a) Exprimer
b) Application numérique. On donne : Débit volumique
b) Application numérique. On donne : Débit volumique
Calculer la différence de pression
c) Expliciter la relation entre la ddp
c) Expliciter la relation entre la ddp
Figure
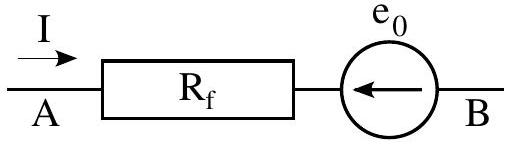
d) L'ensemble est alimenté par un générateur de courant
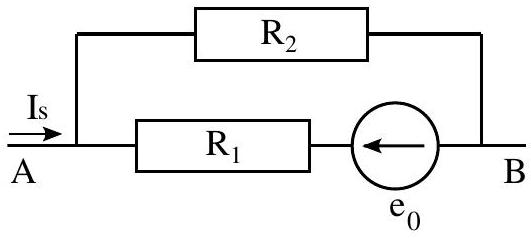
Figure
e) Montrer qu'à débit
f) Application numérique. On donne
2. Conservant la même installation on supprime la source de courant externe. Les électrodes sont reliées par une résistance externe
f) Application numérique. On donne
2. Conservant la même installation on supprime la source de courant externe. Les électrodes sont reliées par une résistance externe
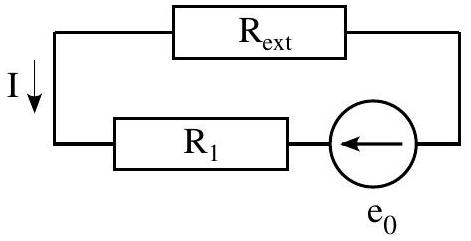
Figure 5
a) Déterminer l'intensité I du circuit en fonction de
b) Calculer la différence de pression entre l'entrée et la sortie; préciser son signe. Quel rôle joue ce dispositif?
b) Calculer la différence de pression entre l'entrée et la sortie; préciser son signe. Quel rôle joue ce dispositif?
Exprimer la puissance mécanique reçue par le fluide en fonction de
c) On définit le rendement
d) Calculer
e) Dans certains réacteurs nucléaires on doit faire fonctionner un circuit primaire contenant un fluide caloporteur, par exemple le sodium liquide qui se trouve être dans ce cas irradié au cœur du réacteur, et un circuit secondaire comportant toujours du sodium mais cette fois non irradié. Le flux dans le circuit primaire est causé par l'énergie thermique venant du réacteur. À partir des propriétés des dispositifs étudiés en 1) et 2), expliquer comment, en couplant ces dispositifs, on peut assurer la circulation dans le circuit secondaire. Quel est l'intérêt d'un tel système du point de vue mécanique?
c) On définit le rendement
d) Calculer
e) Dans certains réacteurs nucléaires on doit faire fonctionner un circuit primaire contenant un fluide caloporteur, par exemple le sodium liquide qui se trouve être dans ce cas irradié au cœur du réacteur, et un circuit secondaire comportant toujours du sodium mais cette fois non irradié. Le flux dans le circuit primaire est causé par l'énergie thermique venant du réacteur. À partir des propriétés des dispositifs étudiés en 1) et 2), expliquer comment, en couplant ces dispositifs, on peut assurer la circulation dans le circuit secondaire. Quel est l'intérêt d'un tel système du point de vue mécanique?
IV. Pompe à induction
On envisage un écoulement de fluide conducteur analogue aux précédents, dans un conduit identique, mais soumis cette fois à un champ magnétique
Ce champ est produit par des bobines plates réparties de part et d'autre du tube (figure 6) alimentées par des courants convenablement déphasés les uns par rapport aux autres. La composante inévitable
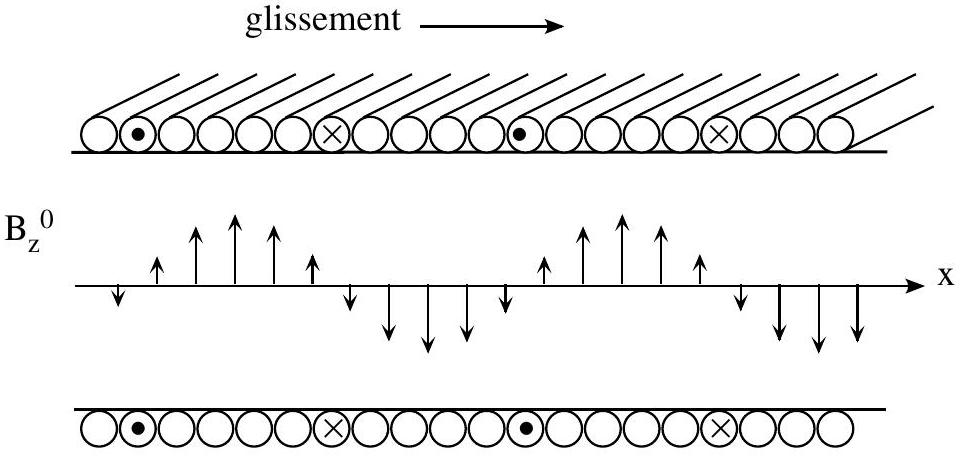
Figure 6
L'étude est effectuée dans l'approximation des régimes quasistationnaires et en régime permanent.
- Dans le fluide en mouvement, il apparaît un courant induit de la forme :
Montrer que le champ magnétique
2. Soit
3. Écrire la loi d'Ohm reliant
4. Exprimer de même
5. Calculer
6. Calculer
7. On suppose
8. Application numérique. On considère l'écoulement, dans un conduit de section rectangulaire, d'un mélange eutectique Na-K de conductivité
2. Soit
3. Écrire la loi d'Ohm reliant
4. Exprimer de même
5. Calculer
6. Calculer
7. On suppose
8. Application numérique. On considère l'écoulement, dans un conduit de section rectangulaire, d'un mélange eutectique Na-K de conductivité
L'amplitude du champ magnétique est
Calculer
9. Quel rôle joue le dispositif si
9. Quel rôle joue le dispositif si
