J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

X ENS Physique PSI 2023

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo x-ens
🔗 Explorer
Banque
X-ENS
Année
2023
Filière
PSI
Matière
Physique
X-ENS PSIX-ENS 2023PSI PhysiquePhysique 2023
2025_09_04_d430671a41ec29bbbdb5g

ÉCOLES NORMALES SUPÉRIEURES
ECOLE POLYTECHNIQUE

CONCOURS D'ADMISSION 2023

MERCREDI 19 AVRIL 2023
08h00-12h00
FILIÈRE PSI
PHYSIQUE (XSR)
Durée : 4 heures
  • L'utilisation de calculatrices n'est pas autorisée pour cette épreuve.

Autour des thermogénérateurs magnétiques

Dans ce problème, nous étudions des dispositifs particuliers appelés thermogénérateurs magnétiques. Après une étude générale des propriétés d'une machine thermique en partie I et II, on s'intéresse aux aspects thermodynamiques plus spécifiques des thermogénérateurs magnétiques dans la partie III et aux propriétés thermodynamiques et magnétiques des matériaux magnétocaloriques utilisés dans les thermogénérateurs en partie IV. Les parties V et VI permettent de comprendre le fonctionnement mécanique du système à partir d'une approche énergétique des forces magnétiques. L'étude du système est complétée par une approche thermique en partie VII et par la présentation du système de détection de la position du matériau magnétocalorique situé à l'intérieur du thermogénérateur dans la partie VIII. Les différentes parties du sujet sont relativement indépendantes entre elles et des résultats intermédiaires permettent d'avancer dans la compréhension du système présenté.

Notations, formulaire et données numériques.

  • Constante universelle des gaz parfaits :
  • Masse molaire de l'air :
  • Capacité thermique massique à pression constante de l'air, considéré comme gaz parfait diatomique :
  • Perméabilité magnétique du vide :
  • Capacité thermique à excitation magnétique constante du Gadolinium :
  • Masse volumique du Gadolinium :
  • Conductivité thermique du Gadolinium :
  • Conductivité thermique du Cuivre :
  • Conductivité thermique de l'air :
  • Quelques données numériques :

I Contexte de la chaleur perdue et machine thermique

Les enjeux de la transition énergétique amènent des réflexions sur l'efficacité des systèmes de production et de conversion de l'énergie, ainsi que sur la récupération d'énergie. Optimiser les systèmes de production d'énergie et récupérer le plus d'énergie possible lors d'une conversion d'énergie deviennent des sujets majeurs dans le cadre d'une politique d'économie d'énergie.
Lors du fonctionnement d'un procédé industriel, l'énergie thermique produite grâce à l'énergie apportée n'est pas utilisée en totalité. Une partie de la chaleur est inévitablement rejetée et non récupérée. En raison de ce caractère inéluctable, on parle de chaleur fatale. Cette quantité d'énergie perdue constitue un gisement potentiel à récupérer.
Cependant, cette appellation est en partie erronée car la chaleur fatale peut être en partie récupérée. L'ADEME (Agence De l'Environnement et de la Maîtrise de l'Energie) classe le gisement de chaleur fatale disponible par écart de température par rapport à la température ambiante (source froide).
Écart de Température Gisement
20 TWh
20 TWh
Tableau 1 - Gisements de chaleur fatale (Energie thermique) disponible par an et classés par écart de température avec la température ambiante, ici prise à .
  1. Rappeler l'expression du premier principe et du deuxième principe de la thermodynamique. Que deviennent ces expressions sur un cycle thermodynamique?
  2. En considérant un système thermodynamique quelconque, noté , en contact avec deux thermostats aux températures et avec , établir les différents régimes de fonctionnement d'une machine thermique idéale. On s'appuiera sur une représentation graphique, appelée diagramme de Raveau, donnant la chaleur échangée entre le système et la source , en fonction de la chaleur échangée entre le système et la source .
  3. Rappeler le nom et la définition des transformations associées à un cycle de Carnot subi par le système en contact avec les deux thermostats précédents. On représentera les étapes du cycle dans le plan ( ) en faisant apparaitre clairement les températures des thermostats.
  4. Dans le cas d'un système subissant un cycle de Carnot, réaliser un bilan d'énergie et un bilan d'entropie, et en déduire l'expression du rendement en fonctionnement moteur en fonction de et .
  5. À partir des données du tableau 1, justifier pourquoi l'ADEME classe les gisements par écart de température par rapport à la température de la source froide et en déduire en Wh l'énergie que l'on pourrait récupérer par an et par gisement.

II Machine de Carnot opérée avec un gaz parfait

Considérons le système précédent comme étant un gaz parfait et subissant un cycle de Carnot entre et , respectivement à et . À chaque état du cycle, le volume, la pression et la température du système sont indicés successivement par et 4 .
L'état 1 du cycle correspond au moment juste avant la phase de compression adiabatique. Dans cet état, le système est dans un volume de (noté ), la pression est de 1 bar (notée ) et sa température est . On notera que sur la phase d'échange de chaleur avec la source chaude, la variation de pression est de 0,4 bar.
On note et les capacités thermiques massiques du système à pression constante et à volume constant, respectivement, en . On rappelle que ces capacités thermiques obéissent à la relation de MAYER : , où est la constante universelle des gaz parfaits, et la masse molaire. On considère dans la suite que le système est constitué d'air, assimilé à un gaz parfait diatomique, tel que l'indice adiabatique vaut .
6. Caractériser qualitativement la variation de pression du système le long du cycle, en détaillant les transformations entre chaque état thermodynamique : et .
7. Donner l'expression de la dérivée pour chaque transformation en fonction de et et représenter les étapes du cycle dans le plan .
8. Exprimer la variation infinitésimale d'entropie du système en fonction des variations de température et de pression, puis en fonction de , et des capacités thermiques massiques. On ne fera pas intervenir dans le résultat le nombre de moles, noté , ni la masse du gaz, notée .
9. Donner l'expression de la pression de l'état en fonction de la pression , et des températures des thermostats, au cours des différentes transformations. En déduire une estimation numérique de la pression pour chaque état thermodynamique du système.
10. Exprimer les chaleurs échangées en fonction de et en fonction de en fonction de . Évaluer numériquement et .
11. En déduire l'expression et la valeur numérique du travail mécanique récupéré pour un cycle moteur. Le résultat paraît-il cohérent avec la valeur obtenue si on utilise l'expression du rendement de Carnot?
12. Les machines thermiques de récupération de chaleur fatale fonctionnent en réalité avec deux transformations isobares pour des raisons techniques. Expliquer pourquoi un fluide subissant une transition de phase (un changement d'état ici) permet d'améliorer l'efficacité de la machine thermique.

III Compromis puissance/efficacité : thermodynamique à temps fini

Historiquement, la thermodynamique a accompagné la révolution industrielle et a été initialement stimulée par le besoin d'optimiser la production d'énergie et d'améliorer l'efficacité des machines thermiques. Cependant, un cycle thermodynamique qui produit le travail maximum, soit le cycle réversible, a besoin d'un temps infiniment long pour échanger de la chaleur sur des transformations isothermes, et produit donc une puissance nulle. La thermodynamique à temps fini étudie comment la contrainte de réalisation d'un cycle en une durée finie va affecter le compromis entre la puissance et l'efficacité.
La figure 1 (figure de droite) décrit le fonctionnement d'un cycle thermodynamique dit endoréversible. Ce dernier possède deux transformations isentropiques et deux transformations à température constante mais à une température qui n'est pas celle des réservoirs (sources) de température. Les sources d'irréversibilité sont uniquement liées aux échanges thermiques avec les sources chaude et froide.
La figure 1 (figure de gauche) décrit un modèle d'échange thermique avec les réservoirs aux températures et , reposant sur des interrupteurs thermiques idéaux et une conductance thermique (en W. ). Ici, la substance active de la machine thermique est alors alternativement en contact thermique avec une zone chaude à la température et une zone froide à la température .
En résumé, les irréversibilités dues à l'échange, avec et , seront quantifiées à partir du modèle d'échange thermique, alors que le cycle dit intérieur entre et sera considéré comme réversible.
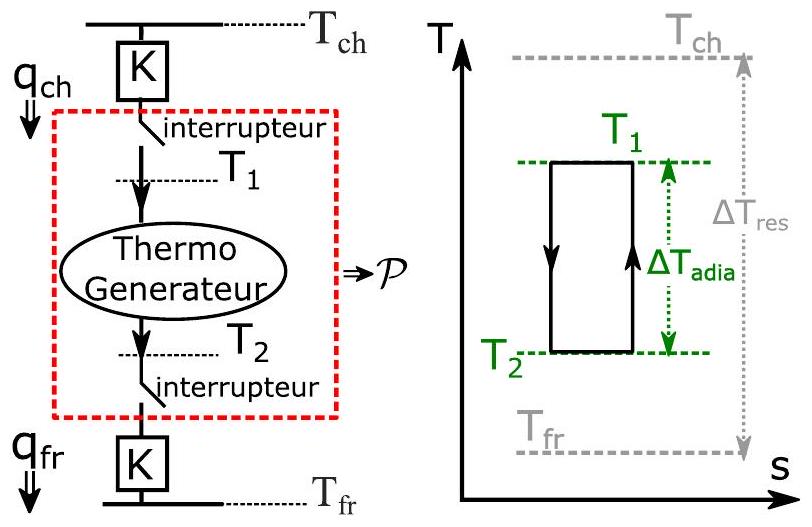
On notera et , et également et , les flux thermiques instantanés (en Watt) échangés respectivement avec la source chaude et la source froide. Les chaleurs moyennes échangées sur un cycle seront notées et (en Joule) et les conventions (différentes de la partie précédente) sont fixées par la figure 1 (figure de gauche). correspond à la puissance moyenne produite sur un cycle.
Figure 1 - (figure de gauche) Description schématique d'un générateur thermomagnétique en prenant en compte un modèle d'échange avec les réservoirs. Les interrupteurs thermiques représentent le fait que la substance active du système est alternativement en contact avec le côté chaud à et le côté froid à ; (figure de droite) Représentation graphique du cycle thermodynamique endoréversible dans un diagramme .
  1. Dans un diagramme ( ), en faisant apparaître les températures des réservoirs, tracer un cycle de Carnot et un cycle endoréversible, puis les comparer.
  2. À partir de la conductance thermique , déterminer l'expression des flux thermiques (instantanés) échangés avec la source chaude et la source froide, respectivement et , le sens du transfert étant indiqué sur la figure 1. En considérant que, lors d'un cycle, la substance active du système est en contact thermique avec le réservoir chaud durant la durée et avec le réservoir froid durant la durée , en déduire les chaleurs échangées et sur un cycle thermodynamique.
  3. En appliquant le deuxième principe de la thermodynamique au cycle endoréversible, en déduire une relation entre le rapport et les différentes températures introduites en figure 1 .
  4. La période du cycle, notée , se décompose en deux durées correspondant aux durées de chaque échange thermique, telle que , les deux transformations isentropiques étant considérées comme instantanées. On définit la puissance produite par le système par l'expression :
Montrer que la puissance se met sous la forme suivante :
où les indices sont à compléter.
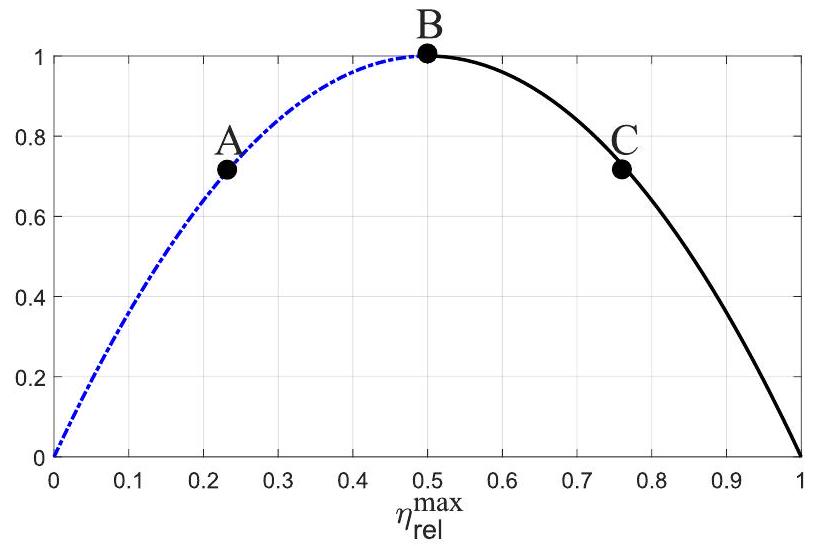
17. Déterminer le rendement du cycle endoréversible ( ) relativement au cycle de Carnot , soit en fonction de et .
Figure 2 - Graphique illustrant le compromis puissance-efficacité.
Après maximisation de la puissance par rapport à , on obtient l'expression de la puissance maximale et du rendement relatif maximal :
avec où est le rendement de CARNOT.
18. Dans le cas d'une récupération d'énergie thermique avec un faible écart de températures, justifier que le rendement de CARNOT est faible, et en déduire une simplification de la puissance maximale ainsi que du rendement relatif maximal.
19. Montrer que pour un fixé, la puissance maximale peut s'exprimer en fonction du rendement relatif maximal , de , de et de . Justifier l'allure de la courbe représentée figure 2 en précisant l'ordonnée du graphique.
20. Dans un diagramme ( ), tracer les cycles correspondants aux points et C . En déduire pourquoi les cycles A et C sont en mesure de produire la même puissance. Préciser, en justifiant, quel point de fonctionnement est le plus intéressant entre A et C .

IV Substance active du système : matériau magnétocalorique

On s'intéresse maintenant à la mise en œuvre d'une machine thermique à partir d'un matériau magnétocalorique qui constitue la substance active du système . Avant d'étudier un thermogénérateur magnétique, soit une machine thermique impliquant un matériau magnétique, on souhaite caractériser plus précisément les propriétés des matériaux magnétocaloriques. La relation constitutive de ces matériaux magnétiques soumis à une excitation magnétique s'écrit avec l'aimantation. Le matériau étant isotrope, les vecteurs et sont tous colinéaires. Les matériaux magnétocaloriques sont des matériaux ferromagnétiques doux qui présentent une dépendance forte de leur courbe d'aimantation à la température. En appliquant le premier principe sur 1 kg de matériau magnétique à l'équilibre thermodynamique, nous obtenons l'expression suivante de la variation infinitésimale d'énergie interne massique :
avec la masse volumique (supposée indépendante de la température ), u l'énergie interne massique, la température du matériau et l'entropie massique. Puisque et sont définis pour 1 kg de substance, nous utilisons des notations minuscules. Ici, la substance dans le système est le Gadolinium, noté Gd. Les données numériques concernant le Gadolinium sont référencées en début du sujet.
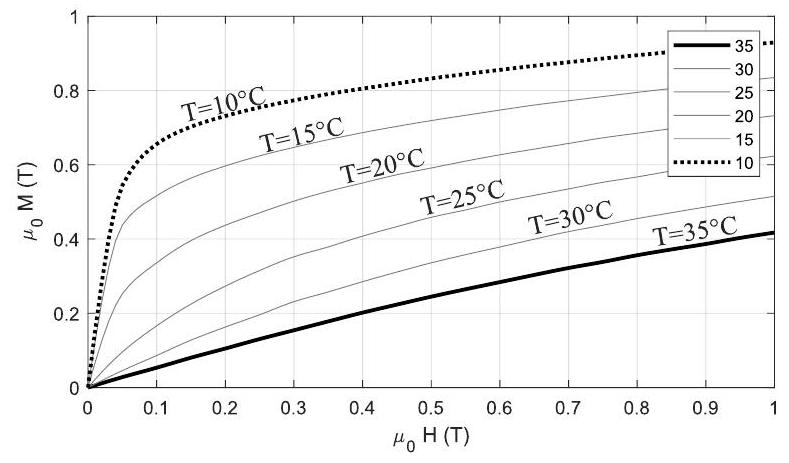
On introduit dans cette partie la fonction thermodynamique enthalpie libre massique dont la définition est .
Figure 3 - Caractéristiques en fonction de d'un matériau magnétocalorique, la légende indique la température en du matériau.
  1. Exprimer la différentielle totale de l'enthalpie libre massique d en fonction des variations infinitésimales de la température et de l'excitation magnétique .
  2. À partir de l'égalité et des propriétés de la différentielle totale de , montrer que si dépend de alors dépend de .
À partir de la représentation graphique de l'aimantation en fonction de l'excitation magnétique du matériau pour différentes températures (figure 3), nous allons approximer les caractéristiques à différentes températures par la relation sur le domaine d'utilisation du matériau. et sont deux constantes telles que et .
23. À partir du modèle de matériau proposé pour , en déduire l'expression de la variation d'entropie massique du matériau, notée , pour un champ variant de 0 à 1 tesla.
24. À partir du deuxième principe de la thermodynamique et de la différentielle totale de , en déduire la variation de température , dans le cadre d'une transformation adiabatique réversible et pour un champ magnétique , variant de 0 à 1 tesla. On introduira la capacité thermique massique à excitation magnétique constante, , et afin de simplifier l'estimation de la variation de température, est supposée constante sur la gamme de température explorée. La température initiale, notée , sera prise à . Après avoir obtenu la variation de température , simplifier l'expression en considérant que tend vers 0 .
25. Sachant que , expliquer pourquoi les thermogénérateurs ont un fonctionnement plus proche de celui de Carnot pour des sources de chaleur avec de faibles écarts de température.

v Étude des forces magnétiques

Dans la suite du sujet, nous étudions le thermogénérateur plus en détail et procédons à des analyses magnétique, mécanique, puis thermique. La figure 4 représente la structure du thermogénérateur, avec une source chaude (en haut), une source froide (en bas), et un matériau magnétocalorique au milieu. La source chaude est constituée du fer, du cuivre et de deux aimants, un aimanté vers le haut et un vers le bas (voir les flèches).
Le matériau magnétocalorique se déplace pour être alternativement en contact avec les aimants (constituant la source chaude), et avec la source froide. La grandeur est une épaisseur d'air qui varie en fonction de la position du matériau magnétocalorique. Quand le matériau est en position haute et en contact avec la source chaude, ; en revanche, pour le matériau en position basse et en contact avec la source froide, on a . Le matériau est relié mécaniquement au bâti de la source froide par l'intermédiaire d'un ressort de constante de raideur . L'air est considéré comme un isolant thermique mais grâce au déplacement du matériau magnétocalorique, un flux de chaleur est transféré de la source chaude à la source froide. Sur la figure 4, on matérialise pour une position quelconque, ni en contact avec la source chaude, ni en contact avec la source froide.
Le cycle thermodynamique de fonctionnement du générateur se décrit en 4 étapes énumérées cidessous :
  • Étape 1 : le matériau est en contact avec la source froide et se refroidit, ce qui induit une augmentation de l'aimantation;
  • Étape 2 : lorsque les forces magnétiques (attraction du matériau magnétocalorique par l'aimant) deviennent prépondérantes sur la force de rappel du ressort, l'équilibre mécanique qui prévalait jusqu'ici est rompu. À cette étape, le matériau est donc en mouvement rapide vers la source chaude;
  • Étape 3 : le matériau est en contact avec la source chaude et se réchauffe, ce qui induit une diminution de l'aimantation;
  • Étape 4 : lorsque les forces magnétiques deviennent faibles devant celle du ressort, l'équilibre mécanique est rompu. À cette étape le matériau est en mouvement rapide vers la source froide.
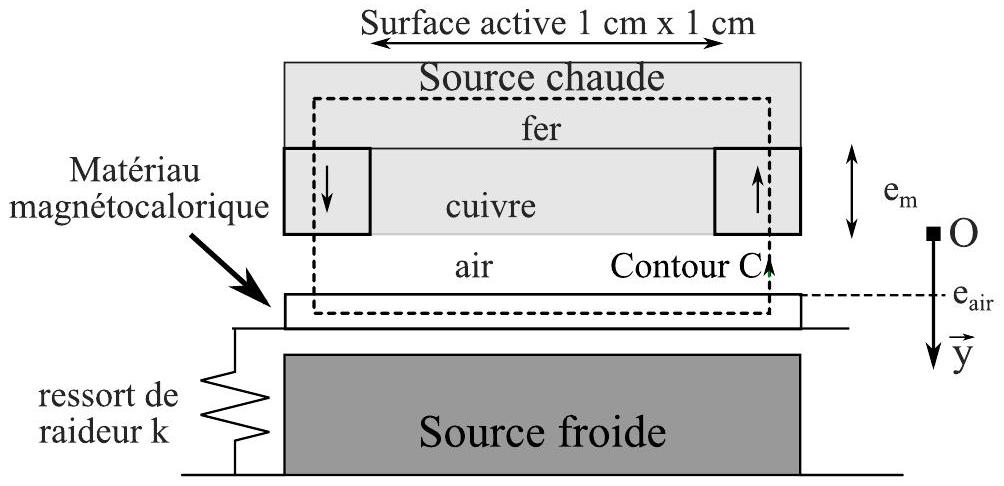
Figure 4 - Structure du thermogénérateur magnétique dans une position quelconque.
On obtient alors une oscillation auto-entretenue.
26. Reproduire la figure 5 et indiquer qualitativement pour les étapes 2,3 et 4 la position du matériau magnétocalorique (dessiner le matériau), la résultante des forces (flèche simple : ) et le flux thermique éventuel entre le matériau et les sources (flèche double : ). L'étape 1 a été complétée pour donner un exemple.
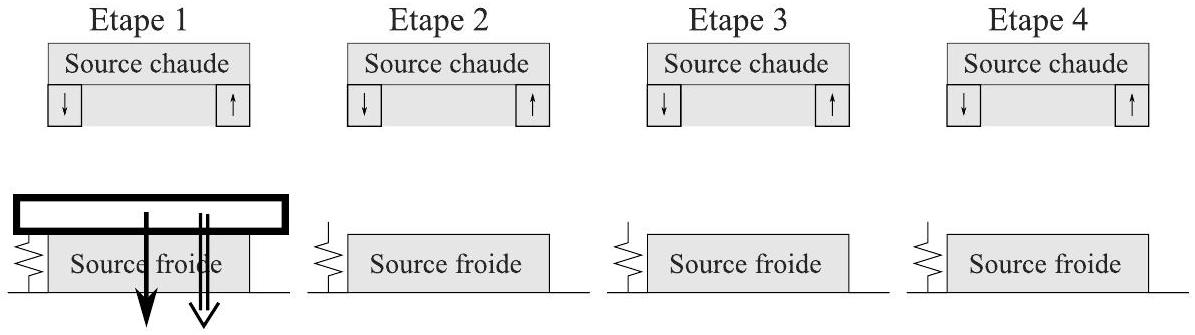
Figure 5 - Différentes étapes du cycle - Les étapes 2, 3 et 4 sont à compléter en reproduisant la figure sur la copie.
Pour déterminer les forces magnétiques en action sur le matériau magnétocalorique, nous utilisons une approche énergétique. On définira les grandeurs magnétiques et géométriques avec les indices {fer, m , air, MC pour désigner respectivement le fer, les aimants, l'air et le matériau magnétocalorique. L'épaisseur d'un aimant est notée et l'épaisseur de la couche d'air est notée .
Pour cette modélisation, l'aimant se comporte comme avec constant et égal à et le fer se comporte comme un matériau ferromagnétique linéaire de perméabilité relative . Le matériau magnétocalorique est lui toujours modélisé par . Pour l'air, on prendra .
Afin de permettre la mise en équation simplifiée du problème, les lignes de champ magnétique sont supposées colinéaires au contour (ligne pointillée sur la figure 4). La longueur de la portion du contour dans le fer est notée et celle de la portion du contour dans le matériau magnétocalorique est notée .
27. Appliquer le théorème d'Ampère sur le contour .
En supposant que les lignes de champ sont parfaitement canalisées dans le fer, les aimants et le matériau magnétocalorique, la conservation du flux du champ d'induction magnétique donne :
où les grandeurs avec air, fer, , désignent les sections du tube de champ dans les matériaux traversés.
28. Montrer que le champ magnétique dans l'air s'écrit sous la forme :
avec à déterminer en fonction des paramètres géométriques.
D'après la géométrie du problème, nous avons . De plus, la perméabilité magnétique du fer étant très élevée, elle est supposée infinie, c'est-à-dire .
29. Simplifier l'expression du champ magnétique et déduire de cette expression que la position du matériau magnétocalorique contrôle en partie le champ appliqué sur le matériau.
L'énergie magnétique d'un système correspond à l'intégrale sur tout l'espace du produit scalaire intégré pour allant de 0 au point de fonctionnement, soit , où est le volume d'intégration. Pour déterminer l'énergie magnétique du système, notée , nous devons déterminer les énergies magnétiques dans le volume correspondant à l'air, au fer, aux aimants et au matériau magnétocalorique à partir de . Ces différentes contributions à l'énergie magnétique seront notées respectivement . Il convient de remarquer que et sont associés à deux volumes.
30. Déterminer l'énergie magnétique dans l'air, en fonction de et des paramètres géométriques, et l'énergie magnétique dans le fer, ces milieux étant supposés linéaires.
31. Déterminer l'énergie magnétique dans les aimants en fonction de et (on rappelle que la relation magnétique est une fonction affine).
32. Déterminer l'énergie magnétique dans le matériau magnétocalorique en fonction de , et .
33. En déduire l'énergie magnétique dans les aimants et dans le matériau magnétocalorique en fonction de et pour les paramètres géométriques en fonction de et .
34. Montrer que l'énergie magnétique du système, , peut s'écrire sous la forme :
où les expressions de et sont à déterminer.
35. On effectue un bilan d'énergie magnétique sur le système. Ce bilan est donné par l'équation suivante :
En déduire l'expression de la force magnétique exercée sur le matériau magnétocalorique. On note la masse du matériau magnétocalorique, et on utilisera l'expression de donnée par l'équation (8). Discuter le sens et la direction de la force magnétique.
36. Expliquer pourquoi la force magnétique dépend de la température. Indiquer quel coefficient varie en fonction de la température dans l'expression de la force .

vi Étude mécanique du thermogénérateur

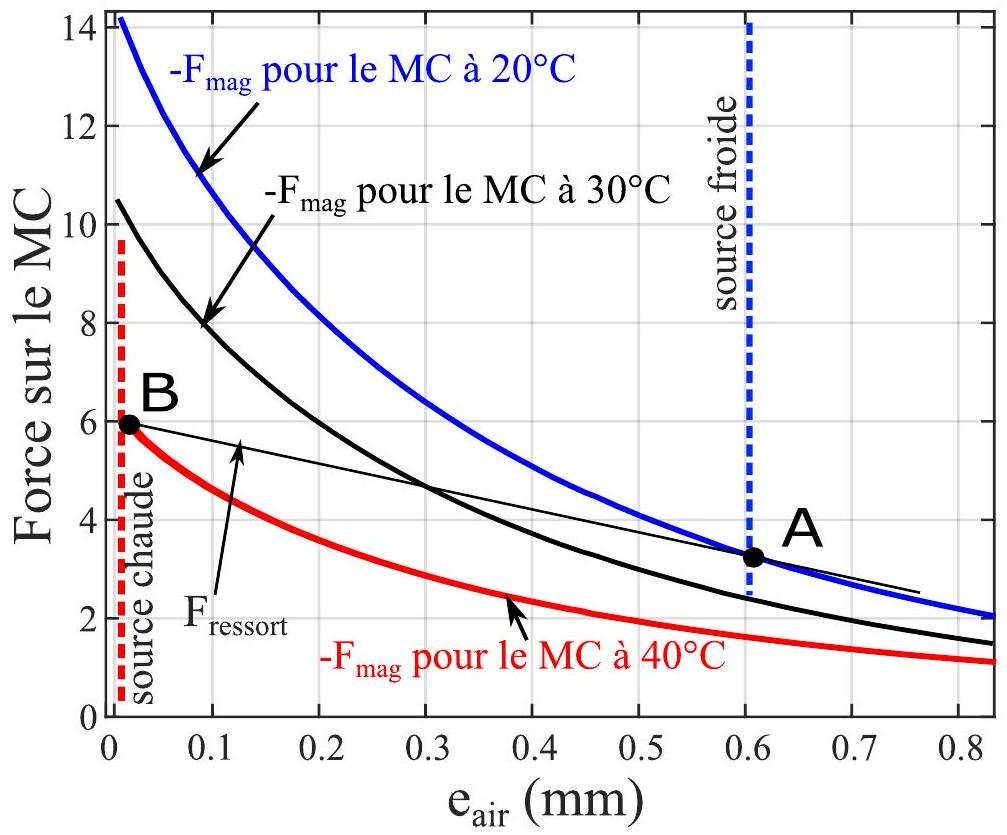
Dans la partie précédente, nous avons étudié la force magnétique en fonction de la position du matériau magnétocalorique. Les forces magnétiques obtenues sont représentées en fonction de et pour différentes températures sur la figure 6. Le matériau magnétocalorique se déplace de la source chaude, soit ( ), vers la source froide, soit ( ), et inversement. La force du ressort est nulle à .
Figure 6 - Représentation graphique de la force du ressort et de l'opposé de la force magnétique appliquées sur le matériau magnétocalorique, en projection sur l'axe de la figure 4.
  1. En reproduisant sur la copie la figure 7 , tracer sur ce graphique force-déplacement le cycle mécanique (trajectoire, sens) emprunté par le matériau magnétocalorique. On fera apparaître sur le cycle mécanique les différentes étapes du cycle thermodynamique associé .
  2. Réaliser un bilan des forces sur le matériau magnétocalorique et appliquer le principe fondamental de la dynamique. On note , la masse du matériau magnétocalorique, la constante de raideur du ressort et la position où la force du ressort est nulle. On rappelle l'existence d'une force de contact telle que , on a , puis et .
  3. Écrire la condition d'équilibre mécanique lorsque le matériau est dans l'étape 1 du cycle. Expliquer pourquoi la force de contact tend vers 0 quand la température diminue.
Le matériau passe de l'étape 1 à 2 au point A de la figure 6 . En ce point, la force de contact est nulle et la force magnétique est opposée à la force du ressort. Afin d'obtenir un système qui transite rapidement vers la source chaude ( ), l'équilibre mécanique doit être instable.
40. En linéarisant le système (développement de Taylor à l'ordre 1) autour du point A , soit en , déterminer les conditions pour que l'équilibre soit instable. Cette condition estelle respectée sur la figure 6 ?
41. Sur la plage , discuter, à partir de la figure 6 , la stabilité des points d'équilibre en fonction de la température. En déduire pourquoi le comportement du système peut être qualifié de bistable >>.
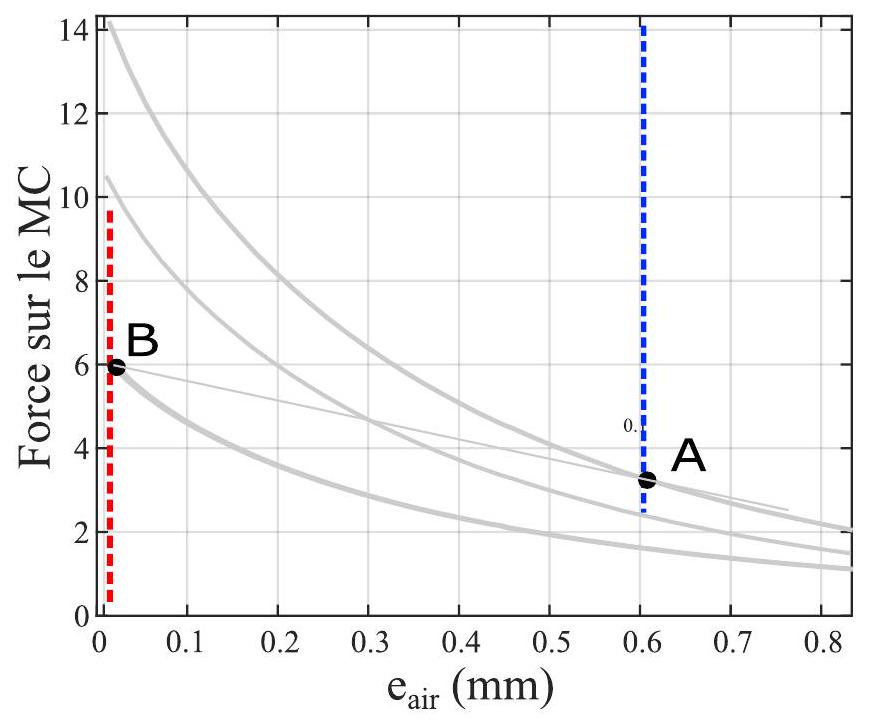
Figure 7 - Graphique force-déplacement à reproduire et à compléter.
  1. Que peut-on dire de et par rapport à la température au point A, notée , et au point B , notée , afin que le système soit en oscillation auto-entretenue entre la source froide et la source chaude?

VII Étude thermique du thermogénérateur

On s'intéresse maintenant à la modélisation thermique du thermogénérateur. Pour cela, on considère le modèle unidimensionnel représenté sur la figure 8 .
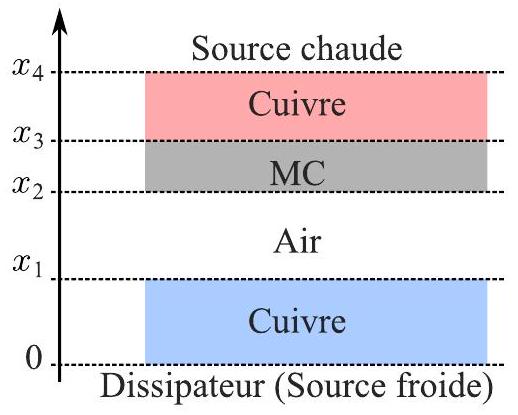
Figure 8 - Modèle thermique unidimensionnel du thermogénérateur.
Dans le prototype de thermogénérateur magnétique, la source chaude est réalisée à l'aide d'une résistance chauffante , infiniment fine de valeur numérique de l'ordre de . Cette résistance est alimentée par un hacheur, comme indiqué sur la figure 9 , dont le rapport cyclique, noté , et la période de découpage, notée , sont tels que :
  • de 0 à , le transistor est fermé;
  • de à le transistor est ouvert.
Puisque la période de découpage est bien plus petite que la réponse thermique du système, dans la modélisation thermique on ne prendra en compte que la puissance moyenne produite par la résistance, notée . La tension d'alimentation du hacheur, notée , vaut 10 V .
La chaleur produite par la résistance chauffante passe ensuite au travers du générateur thermomagnétique puis est dissipée dans l'air au travers d'un dissipateur thermique.
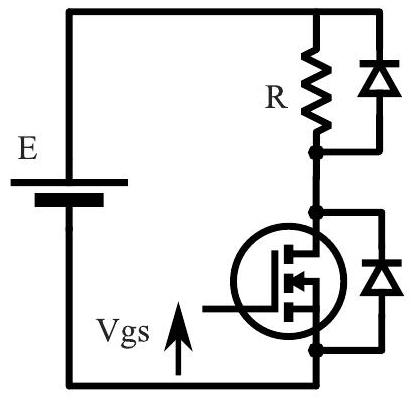
Les épaisseurs, les conductivités thermiques et les capacités thermiques volumiques des éléments sont notés et respectivement, avec l'indice correspondant aux matériaux qu'elles modélisent : air, cuivre ou MC. Les deux éléments en cuivre sont chacun d'épaisseur , alors que le matériau magnétocalorique (MC) et l'air sont d'épaisseur . Les surfaces des différents éléments précédents sont de .
Figure 9 - Schéma électrique de l'alimentation de la résistance associée à la source chaude.
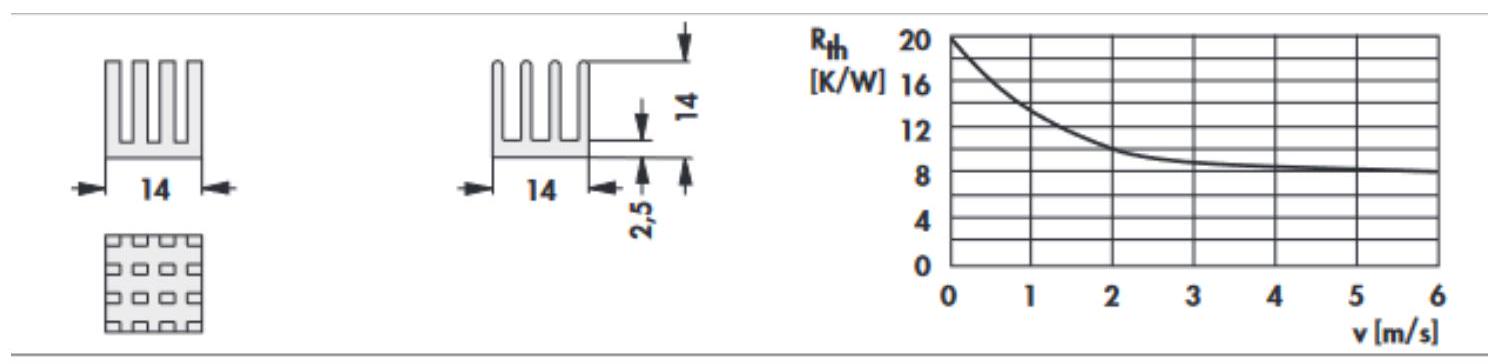
Les caractéristiques du dissipateur, placé à , sont données sur la figure 10. L'ensemble du dissipateur est modélisé par une résistance thermique, notée , entre l'air à la température et la surface du thermogenerateur à la température . On considère ici qu'il n'y a pas de convection forcée. Le dissipateur échange de la chaleur avec l'air à la température . Dans cette étude, on considère le matériau magnétocalorique fixe et en contact avec la source chaude.
Figure 10 - Extrait de la documentation technique du dissipateur.
  1. Déterminer la puissance produite par la résistance et en déduire une relation entre et .
  2. Rappeler l'équation de la diffusion thermique en régime dépendant du temps dans le cas d'un modèle unidimensionnel dans les matériaux de la figure 8. Définir les conditions aux limites à l'interface avec le dissipateur, avec la résistance chauffante et à l'interface entre les différents matériaux. Les phénomènes de convection dans la couche d'air située entre les abscisses et sont négligés.
  3. En déduire les températures et en régime permanent.
  4. En relation avec l'analyse de stabilité de la partie précédente, en déduire un encadrement de la puissance permettant les oscillations auto-entretenues du matériau magnétocalorique en fonction de et .
  5. En se plaçant à une température égale à , déterminer un encadrement du rapport cyclique pour lequel on obtient une oscillation de la structure magnétocalorique (on donnera un encadrement de par des valeurs numériques avec un seul chiffre significatif).

VIII Capteur de position pour l'étude du système

Les études précédentes du thermogénérateur magnétique montrent l'importance de la position du matériau magnétocalorique dans le fonctionnement du dispositif. Il est donc en général important de connaître la position du matériau magnétocalorique avec précision. Pour ce faire, un capteur de position, fonctionnant par effet capacitif, est intégré au dispositif. Il est modélisé sous la forme d'un système de deux condensateurs déformables comme celui présenté sur la figure 11 où la plaque du haut correspond à la source chaude, la plaque du milieu au matériau magnétocalorique et celle du bas à la source froide. 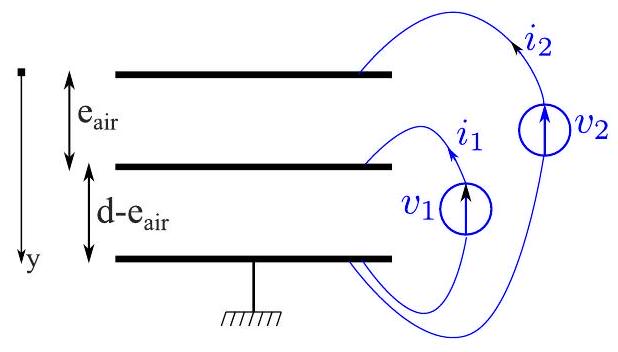Ces trois plans parallèles conducteurs sont de surface et séparés respectivement de et de ( ). Pour éviter un court-circuit lors du contact, les électrodes sont recouvertes d'un isolant infiniment fin. Les condensateurs étant déformables, leurs capacités sont variables.
Figure 11 - Schéma de principe du capteur de position proposé.
  1. Dans un système formé de deux électrodes planes parallèles de surface et de distance , donner la relation entre le champ électrique (sens, direction, valeur) et la charge portée par les armatures.
  2. En déduire la capacité du système entre les deux électrodes.
  3. Réaliser un schéma électrique équivalent de la structure proposée en figure 11, en faisant intervenir la notation pour le condensateur du bas et pour le condensateur du haut. Indiquer les expressions de et en fonction de . On rappelle que est une quantité physique pouvant varier dans le temps.
  4. À partir de l'équation liant une charge au courant , et de la relation de comportement d'un condensateur, en déduire la relation entre la tension du condensateur et le courant dans le cas général où la capacité du condensateur, notée , dépend du temps.
  5. Déterminer deux équations différentielles ordinaires reliant et à et .
Dans la suite de la partie, nous mesurons directement les grandeurs et et nous utilisons par la suite uniquement ces grandeurs physiques.
53. Réécrire le système d'équations obtenu à la question (52), en fonction de et .
54. Afin d'avoir directement accès aux grandeurs physiques d'intérêt, soit et , expliquer comment disposer des sondes de mesure de courant et de tension sur le schéma représenté figure 11.
55. Dans la situation où on impose et , donner l'expression des courants mesurés lorsque le matériau magnétocalorique se déplace avec une vitesse . On notera la vitesse de la plaque centrale telle que .
56. À partir du raisonnement précédent et si on doit mesurer la position de la plaque centrale, quel inconvénient ou problème pouvons-nous rencontrer avec cette technique?
On impose maintenant et en prenant des grandeurs sinusoïdales. On pose pour cela et , avec la pulsation.
57. Donner l'expression des courants mesurés lorsque le matériau magnétocalorique se déplace à une vitesse .
58. En comparant à la situation où les tensions et ne sont pas sinusoïdales, préciser les avantages et/ou les inconvénients de la méthode où les tensions sont sinusoïdales.
59. À partir de fonctions électroniques comme la soustraction, l'addition, la multiplication ou des fonctions de filtrage, proposer un schéma électrique pour extraire les composantes utiles du signal, qui après traitement numérique permettront de remonter à la vitesse et à la position. On justifiera succinctement le choix des paramètres des dispositifs utilisés.
X ENS Physique PSI 2023 - Version Web LaTeX | WikiPrépa | WikiPrépa