Ce sujet aborde la structure de l'atmosphère sous l'angle de la thermodynamique. Il comporte trois parties. Bien que le contexte général soit établi dans la première partie, les trois parties du sujet peuvent être abordées indépendamment. Certaines définitions et relations de thermodynamique sont rappelées en annexe à la fin du texte, ainsi que les valeurs de certaines grandeurs apparaissant dans les applications numériques. Les résultats des applications numériques seront donnés avec un seul chiffre significatif, à l'exception des trois premières questions pour lesquelles on donnera deux chiffres significatifs.

1 Structure verticale de l'atmosphère

On considère dans cette section des modèles d'atmosphères de complexité croissante, afin d'isoler les processus physiques qui gouvernent le profil de température vertical de l'atmosphère. On considère tout d'abord les processus radiatifs : on admet qu'un système plan infini à température

émet par rayonnement un flux surfacique d'énergie

(en watts par mètre carré), le flux étant dirigé vers l'extérieur. Dans les situations considérées ci-après, ce flux correspond à du rayonnement infrarouge. Le coefficient

est appelé constante de Stefan. On néglige la courbure de la Terre dans cette première partie, et on considère donc la surface de la Terre comme localement plate.

Dans un premier modèle, on considère que la surface terrestre absorbe un flux solaire incident , considéré uniforme et indépendant du temps. A l'équilibre, la Terre réémet l'intégralité de l'énergie reçue par rayonnement vers le haut. En déduire la température d'équilibre de surface de la Terre dans ce modèle. Faites une application numérique en vous aidant de l'annexe. Commentez le résultat.
Un raffinement du modèle consiste à inclure une atmosphère infiniment fine située à une hauteur au-dessus de la surface de la Terre. Cette atmosphère est transparente au rayonnement solaire incident, mais elle est entièrement absorbante pour le rayonnement infrarouge émis par la Terre. Elle atteint une température d'équilibre , si bien qu'elle rayonne elle aussi un flux d'énergie vers le haut, mais aussi un flux vers le bas. Calculez la température d'équilibre de l'atmosphère, ainsi que la nouvelle température d'équilibre de surface de la Terre. Faites une application numérique en vous aidant de l'annexe. Commentez le résultat obtenu. Comment s'appelle l'effet mis en évidence par ce modèle simple ?

On oublie un instant les modèles radiatifs précédents, pour se concentrer sur la thermodynamique du fluide atmosphérique. On suppose que l'atmosphère est un gaz parfait diatomique.
3) Rappelez quels sont les deux constituants principaux de l'atmosphère ainsi que leurs proportions. En déduire une valeur approchée de la masse molaire moyenne

de l'air.

On donne la différentielle de l'entropie du gaz parfait:

où

, et

désignent l'entropie, la température et la pression du gaz. On désigne de plus par

la quantité de matière (nombre de moles), et on définit

, où

est la capacité calorifique molaire à pression constante du gaz, et

est sa capacité calorifique molaire à volume constant. Ces deux grandeurs sont également reliées par la relation de Mayer, rappelée en annexe.
4) On s'intéresse au modèle isentropique, pour lequel l'entropie du gaz est supposée indépendante de la coordonnée verticale

. Ecrire tout d'abord l'équilibre hydrostatique d'une parcelle d'atmosphère, puis calculer le profil de température

associé à ce modèle, en fonction de la température

à la surface

de la Terre, de l'accélération

de la pesanteur (supposée constante), de la capacité calorifique molaire

de l'air (supposée constante également), et de la masse molaire moyenne

de l'air.
5) Faites une application numérique pour le gradient de température

dans ce modèle. On pourra considérer l'air comme un gaz parfait diatomique.

On souhaite justifier la pertinence de ce modèle d'atmosphère isentropique. Dans ce but, on considère une atmosphère ayant un profil de température initial

quelconque (les profils de densité

et de pression

se déduisent de ce profil de température par l'équilibre hydrostatique et la loi des gaz parfaits). On isole une parcelle de fluide à l'altitude initiale

qui constitue le système fermé étudié. Ce système est initialement à la température

, et à la pression

. On suppose qu'une perturbation externe déplace la parcelle considérée à l'altitude

, de façon adiabatique et quasi-statique (réversible), où

représente un déplacement infinitésimal. Le système s'équilibre donc rapidement à la pression

.
6) Calculez la température

du système à l'issue de cette transformation, en fonction de

.
7) Discutez le mouvement vertical ultérieur de la parcelle d'atmosphère, selon que

. Quelle situation correspond à une atmosphère stable ? à une atmosphère instable ? On appelle ce phénomène l'instabilité convective.
8) Le cas où

s'appelle le cas "marginalement stable". Quel est le gradient de température vertical

de l'atmosphère dans cette situation marginalement stable ? Commentez, en lien avec les questions 4) et 5).

On revient à un modèle purement radiatif, que l'on complexifie en prenant en compte l'absorption et la ré-émission de rayonnement par chaque tranche élémentaire d'atmosphère. Pour un profil donné du coefficient d'absorption de rayonnement infrarouge par l'atmosphère, ce modèle conduit au "profil radiatif" de température représenté en figure 1.
9) Après avoir estimé le gradient de température dans les hautes et basses couches de ce modèle

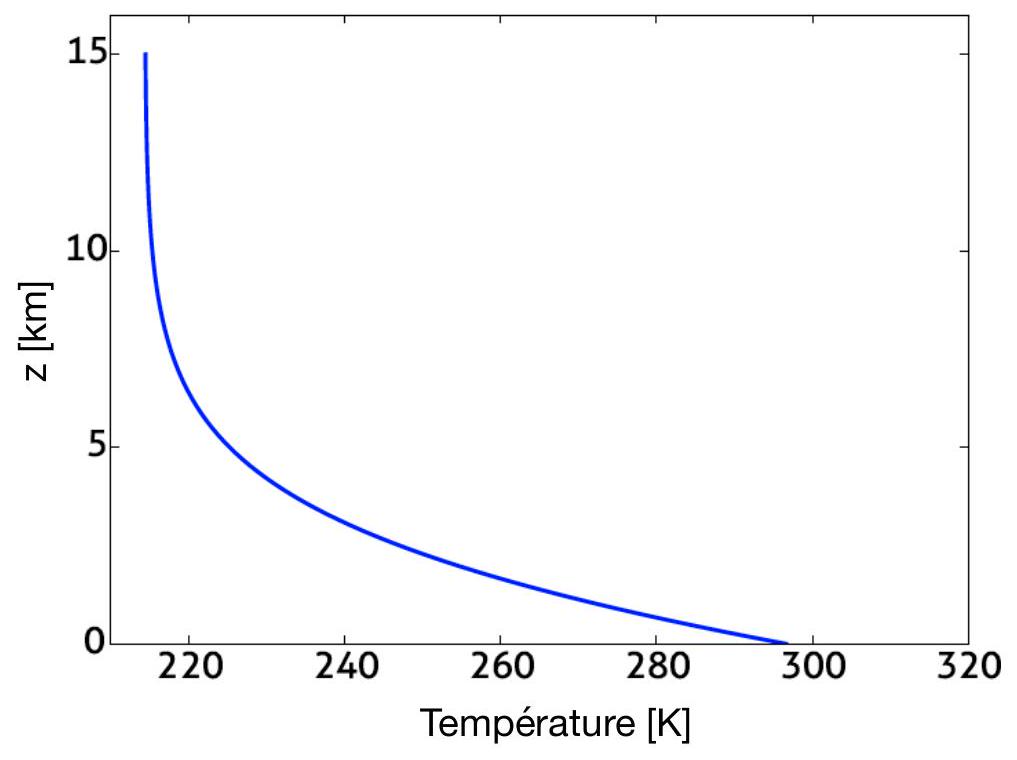
Figure 1: Profil vertical de température issu d'un modèle purement radiatif prenant en compte l'absorption et la ré-émission de chaque couche infinitésimale d'atmosphère.

d'atmosphère, indiquez approximativement quelle partie de l'atmosphère est stable, et laquelle est instable, suivant ce modèle.

Le phénomène d'instabilité convective fait que le modèle purement radiatif de la figure 1 n'est pas satisfaisant. A terme, l'instabilité convective conduit à des mouvements erratiques de l'air qui affectent fortement le profil de température mesuré dans l'atmosphère réelle. On prend en compte ce phénomène en admettant qu'à toute altitude

où le profil de température est instable, ces mouvements erratiques se produisent jusqu'à ce que le profil de température retrouve localement un gradient de température proche (mais légèrement plus faible, comme nous l'expliquerons dans les questions suivantes) du gradient marginalement stable déterminé à la question 8). Cette région de l'atmosphère où l'instabilité convective joue un rôle prépondérant s'appelle la troposphère. La couche d'atmosphère qui n'est pas affectée par cette instabilité s'appelle la stratosphère.
10) Commentez alors l'allure qualitative du profil de température du modèle simplifié d'atmosphère standard utilisé en aéronautique et fourni en figure 2, en lien avec le profil du modèle purement radiatif de la figure 1. Identifiez en particulier la troposphère et la stratosphère.

Le gradient de température mesuré dans la troposphère est moins raide aux latitudes équatoriales. La présence d'humidité dans l'atmosphère permet d'expliquer ce phénomène. On considère alors un système fermé constitué d'une parcelle d'atmosphère contenant un mélange air-vapeur d'eau. On note

la quantité de matière (nombre de moles) de vapeur et

le nombre de moles d'air dans le système. Le rapport

désigne la fraction molaire de vapeur d'eau dans la phase gazeuse. Cette fraction est supposée très faible devant

. On admet que lorsqu'il y a condensation, l'eau liquide apparaît sous la forme de fines gouttelettes qui restent en suspension dans la parcelle d'atmosphère, et qui ne tombent pas sous l'effet de la gravité.

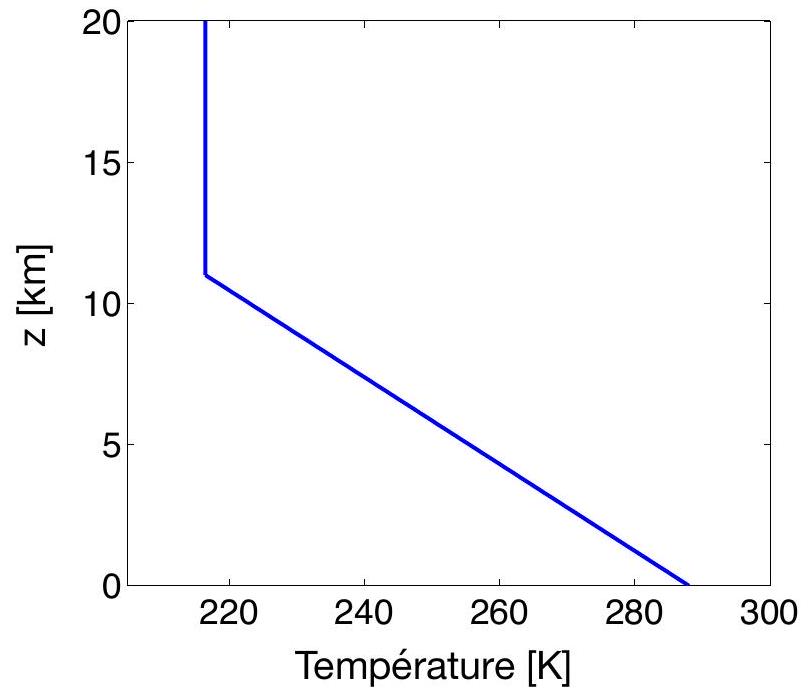
Figure 2: Profil vertical de température du modèle international d'atmosphère standard utilisé en aéronautique.

On considère cette parcelle d'atmosphère à une altitude donnée dans le profil de température marginalement stable calculé à la question 8). On suppose de plus que cette parcelle est initialement à la pression de vapeur saturante en vapeur d'eau. On imagine que cette parcelle subit un léger déplacement vers le haut, de façon quasi-statique et adiabatique (réversible). Expliquez qualitativement pourquoi, sous certaines conditions, la parcelle peut néanmoins continuer son mouvement ascendant alors même que l'atmosphère environnante n'est pas instable vis-à-vis du critère déterminé à la question 7). Que voit-on alors apparaitre dans le ciel ?
Proposez une expression approchée pour en fonction de et uniquement, lorsque la quantité de vapeur en phase gazeuse varie. On utilisera cette expression approchée dans ce qui suit.
On étudie l'évolution de la parcelle au cours de son mouvement ascendant, toujours supposé quasi-statique et sans transfert thermique avec l'atmosphère environnante, dont le profil de température est maintenant considéré arbitraire. On considère toujours , si bien que l'on peut continuer à décrire la phase gazeuse par la relation (1), dans laquelle on remplacera par (on néglige donc la vapeur dans l'évaluation de la densité, de la quantité de matière et de la masse molaire de la parcelle). Dans cette relation, la variation d'entropie est donnée par , où est l'enthalpie libérée par la condensation. En combinant cette relation avec l'équilibre hydrostatique, montrez alors que :

où

sont respectivement la température et la fraction molaire de vapeur dans la phase gazeuse, lorsque la parcelle passe à l'altitude

est l'enthalpie molaire de vaporisation de l'eau. Elle est considérée constante dans ce qui suit, de même que

Au voisinage immédiat de l'océan équatorial, l'air se charge en vapeur d'eau jusqu'à satu-

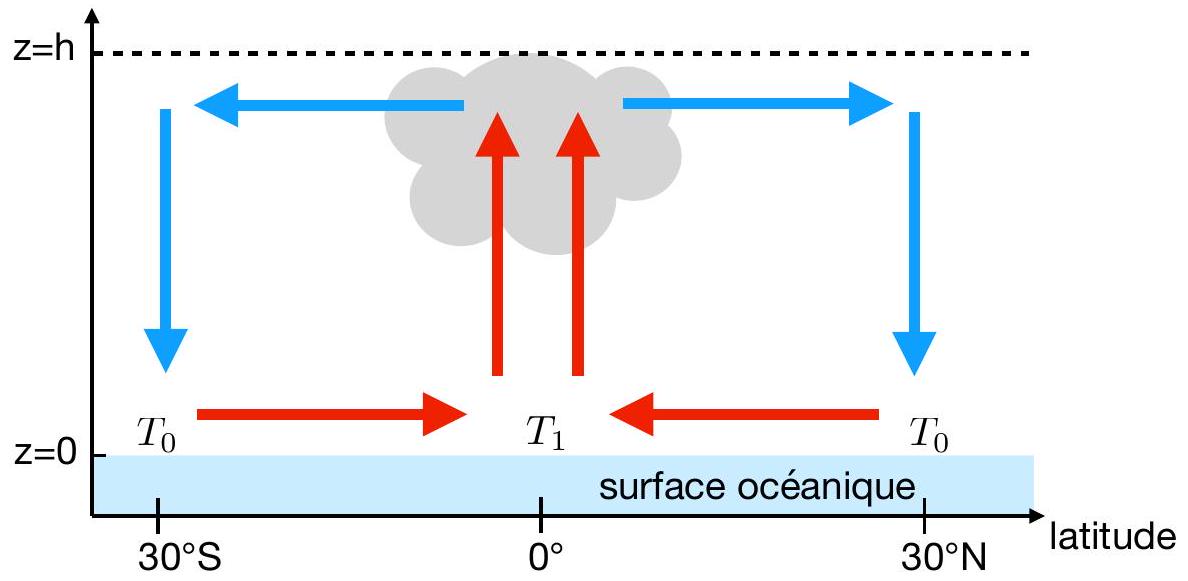
Figure 3: La circulation de Hadley correspond aux mouvements atmosphériques dominants dans un plan méridional (latitude - altitude). La température de surface au niveau de l'océan est supérieure au voisinage de l'équateur (

) qu'aux latitudes subtropicales (

). Les flèches illustrent la direction dominante du vent.

ration. La fraction molaire en vapeur d'eau initiale,

, est alors de

, et la température de l'ordre de

. Cette atmosphère humide consiste en de nombreuses parcelles isolées d'atmosphère, identiques au système précédent, qui ont un mouvement ascendant depuis le niveau de la mer

jusqu'au sommet de la troposphère, à une altitude

. On suppose que toute la vapeur est condensée lorsqu'une telle parcelle atteint l'altitude

.
14) Calculez alors le gradient de température moyen

en fonction de

, et

est appelé le "gradient de température de l'atmosphère humide".
15) Donnez la valeur numérique du gradient de température de l'atmosphère humide

, en considérant l'atmosphère comme un gaz parfait diatomique. On donne l'enthalpie de vaporisation de l'eau :

. Commentez le résultat, en lien avec le profil du modèle international d'atmosphère standard fourni en figure 2.
16) On représente sur la figure 3 la circulation de Hadley, qui est le principal courant méridional de l'atmosphère au voisinage de l'équateur. Pourquoi la température de surface est-elle supérieure au voisinage de l'équateur (

), par rapport aux latitudes subtropicales (

)? Commentez alors la structure de cette circulation : direction des mouvements d'air, présence de précipitations équatoriales, etc.

On souhaite établir la dépendance de la pression de vapeur saturante de vapeur d'eau

avec la température. Pour cela, on considère un système fermé, formé uniquement d'eau liquide et de vapeur d'eau en co-existence (sans air). On note

l'enthalpie libre molaire de la phase liquide et

celle de la phase vapeur. De même, on note

les volumes molaires de ces deux phases, et

leurs entropies molaires.
17) Exprimez la différentielle de

en fonction de

, et des diffé-
rentielles de

. Exprimez de même la différentielle de

en fonction de

, et des différentielles de

. En utilisant l'extensivité de l'enthalpie libre

du système complet, donnez son expression en fonction de

, de la quantité de matière en phase vapeur

et de la quantité de matière totale

.
18) On considère la situation où

sont imposées par un thermostat et un réservoir de pression. On admet que

est un potentiel thermodynamique dans cette situation. Exprimez alors la condition d'équilibre liquide-vapeur en fonction de

.
19) On considère deux points sur la courbe de coexistence liquide-vapeur, de coordonnées (

) et (

). Ecrire la condition d'équilibre liquide-vapeur aux deux points considérés en fonctions des enthalpies libres molaires des deux phases. Soustraire ces deux conditions d'équilibre pour obtenir la relation de Clapeyron :

En déduire le sens de variation de la pression de vapeur saturante avec la température.
20) On néglige le volume molaire de la phase liquide devant celui de la phase gazeuse, et on assimile la vapeur à un gaz parfait à la pression

. On considère de plus que

est indépendante de la température. Montrez alors que la pression de vapeur saturante s'exprime sous la forme :

où

est une température de référence arbitraire, et où vous donnerez l'expression de

.
21) On considère que l'eau existe dans l'océan et l'atmosphère sous deux formes,

, formées respectivement avec les isotopes 16 et 18 de l'oxygène. Ces deux isotopes sont stables du point de vue de la radioactivité. Les deux types de molécules d'eau se caractérisent par des enthalpies molaires de vaporisation différentes, et donc des pressions de vapeur saturante différentes. Expliquez comment la fraction de

dans les calottes glaciaires fournit un historique de la température de l'atmosphère terrestre.

2 La troposphère vue comme une machine thermique

On se propose de modéliser le courant atmosphérique représenté sur la figure 3 par une machine thermique cyclique. La thermodynamique nous permet alors de déterminer une borne supérieure sur la fraction du transfert thermique incident qui est transformée en travail mécanique sous la forme de vents. Dans ce but, on revient dans un premier temps sur le fonctionnement et le rendement des moteurs dithermes cycliques. Pour les applications numériques demandées dans les deux dernières questions de cette partie, on considèrera la Terre comme une sphère dont le rayon vaut approximativement 6400 km .
22) On considère tout d'abord un moteur ditherme cyclique en interaction avec un thermostat chaud de température

et un thermostat froid de température

. Définissez le rendement

de ce moteur. Etablissez la valeur théorique maximale

de ce rendement (le rendement de Carnot), atteinte si les transformations associées au cycle sont réversibles.

Une machine thermique entièrement réversible n'est pas un bon modèle d'une machine réelle : les processus mis en jeu doivent être infiniment lents, en particulier les transferts thermiques. Si le travail fourni par la machine est non nul, ce travail est fourni en un temps infini ! Autrement dit, la puissance engendrée (travail fourni par unité de temps) tend vers zéro dans la limite de transformations parfaitement réversibles. Pour résoudre ce problème on considère la situation représentée sur la figure 4. La machine comprend un fluide, le système

à l'intérieur du cadre pointillé, qui subit de façon cyclique 4 transformations :

Une étape isotherme, à température , pendant laquelle le fluide reçoit un transfert thermique algébrique depuis le thermostat chaud, à température . Le thermostat est connecté au système par une résistance thermique . Cette étape est supposée durer un temps . On notera que la température au voisinage immédiat du système (au bord du domaine pointillé) est bien : c'est la température effective de la source chaude pour le système .
Une détente adiabatique rapide du fluide. Si nécessaire, une telle détente peut être effectuée rapidement tout en restant réversible (il suffit que le temps soit long devant le temps de propagation des ondes sonores dans le fluide). Sa durée est donc négligeable par rapport au temps .
Une étape isotherme, à température , pendant laquelle le fluide reçoit un transfert thermique algébrique , à travers une résistance thermique , depuis un thermostat froid à température . Cette étape dure un temps égal à celui de l'étape 1. On notera encore une fois que la température au voisinage immédiat du système est : c'est la température effective de la source froide pour le système .
Une compression adiabatique rapide du fluide (qui peut néanmoins être réversible, si nécessaire), dont la durée est négligeable par rapport au temps .

On note

le travail algébrique reçu par le système pendant un cycle. Les températures des thermostats

sont fixées, mais on suppose que l'on peut ajuster les températures de fonctionnement

du moteur pour obtenir un fonctionnement optimal.
23) Donnez les signes de

dans ce qui vous semble être le régime de fonctionnement normal du moteur. Ordonnez les températures

dans ce régime de fonctionnement, en justifiant très brièvement. On supposera cet ordre des températures respecté dans la suite.
24) Exprimez les transferts thermiques algébriques

reçus par le système

pendant les étapes 1 et 3 , en fonction de

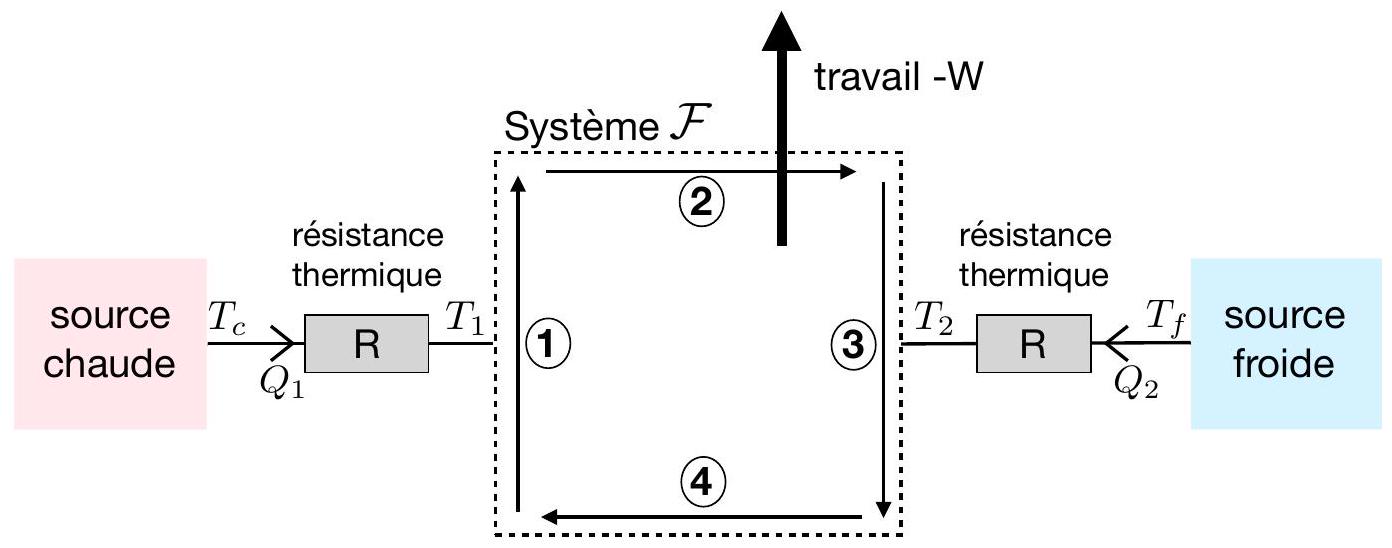
Figure 4: Une machine cyclique est connectée aux sources chaude et froide par le biais de résistances thermiques. Le système

subit alors de façon cyclique les 4 étapes décrites dans le texte, représentées schématiquement par les chiffres entourés.

Définissez la puissance motrice fournie par le moteur. Exprimez en fonction de , et .
A l'aide du second principe de la thermodynamique, établir une inégalité entre et . Pour simplifier les calculs, on admet que le rendement maximal est obtenu lorsque les transformations sont réversibles pour le système . On remplacera alors cette inégalité par une égalité dans ce qui suit.
A l'aide des réponses aux deux questions précédentes, éliminez pour exprimer la puissance sous la forme :

où l'on a introduit les paramètres

.
28) A l'aide des réponses aux questions précédentes (en particulier la question 23), montrez que

.
29) En pratique, les moteurs réels fonctionnent dans un régime où

(et donc

) est choisie pour maximiser la puissance motrice délivrée, à

fixées. Calculez la valeur

associée à ce maximum, en fonction de

. Donnez la valeur du maximum de puissance en fonction de

.
30) Donnez l'expression du rendement

du moteur en fonction de

. Montrez que le rendement du moteur à puissance maximale vaut

. Comment cette expression du rendement se compare-t-elle au rendement de Carnot ?
31) La différence de valeur entre ces deux rendements signifie que certains processus apparaissant sur la figure 4 sont irréversibles. Quels sont-ils ? On définit le taux de création d'entropie

comme le rapport de l'entropie créée par ces processus irréversibles pendant un cycle divisée
par la durée d'un cycle. En appliquant le second principe de la thermodynamique à un système judicieusement choisi, calculez

en fonction de

dans le régime de fonctionnement à puissance maximale du moteur.

On souhaite appliquer le modèle précédent aux courants atmosphériques. Le système est la totalité de la troposphère, que l'on considère comme une couche de fluide de hauteur

à la surface de la Terre, et de densité

considérée constante pour ces calculs d'ordre de grandeur. Le transfert thermique

reçu par la troposphère est dû au rayonnement solaire incident qui atteint la surface terrestre. Ce rayonnement a une intensité

en moyenne sur une journée et sur toute la surface de la Terre.

correspond alors au transfert thermique sous forme de rayonnement infrarouge émis au niveau du sommet de la troposphère (on néglige la stratosphère), tandis que

est l'énergie qui est transformée en travail moteur sous la forme de vents, ou courants atmosphériques. La température moyenne au niveau du sol est

, tandis que la température moyenne au sommet de la troposphère est

.
32) En supposant que le système fonctionne à puissance maximale, calculez approximativement l'énergie cédée aux vents et courants atmosphériques par unité de temps.
33) On admet que les courants atmosphériques ainsi engendrés dissipent leur énergie cinétique à un taux

(énergie dissipée par unité de temps), de l'ordre de

, où

est la masse totale de la troposphère et

la vitesse typique des courants atmosphériques. En déduire un ordre de grandeur de

. Commentez.

3 Nucléation et formation des nuages

On s'intéresse à la formation des nuages, et on considère donc un système constitué d'eau liquide et d'un mélange gazeux air-vapeur d'eau. On note

la pression partielle de vapeur dans le gaz, et

la pression de vapeur saturante.
34) Donnez la relation entre le potentiel chimique

de l'eau liquide, supposé ne dépendre que de la température, et le potentiel

de la vapeur d'eau à la pression de vapeur saturante ?

On considère maintenant une pression de vapeur quelconque, et on s'intéresse à l'évolution d'une gouttelette d'eau liquide dans l'atmosphère. L'existence d'une interface de surface

entre le liquide et le gaz conduit à un terme d'énergie de surface supplémentaire,

, qu'il convient d'ajouter à l'énergie du système (ou au potentiel thermodynamique considéré). Le coefficient

est une constante positive appelée tension de surface. Son unité est le

. Le système considéré contient un nombre fixe de molécules d'air, et un nombre total fixe

de moles d'eau, où

est le nombre de moles d'eau liquide et

le nombre de moles de vapeur d'eau. Le système est maintenu à pression et température constante.
35) Exprimez la différentielle de l'enthalpie libre du système en fonction de

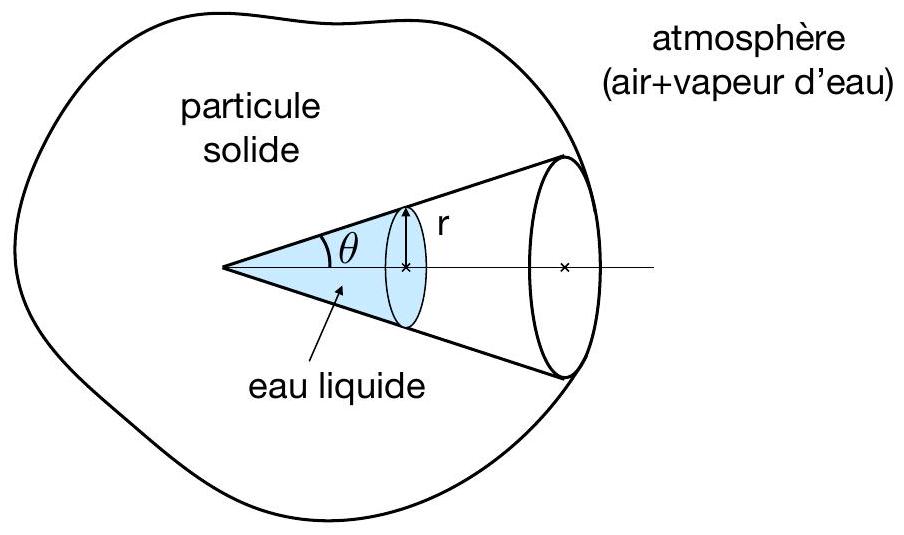
Figure 5: Une particule fine solide comporte une cavité conique ouverte sur l'extérieur. On considère la possibilité que de l'eau liquide apparaisse sous la forme d'un domaine conique au fond de la cavité.

et/ou leurs différentielles.
36) On suppose que la phase liquide consiste à tout instant en une gouttelette d'eau sphérique de rayon

et de masse volumique constante

. Exprimez la différentielle de l'enthalpie libre en fonction de

, où

est la masse molaire de l'eau.
37) Intégrez cette relation pour obtenir l'enthalpie libre

(à une constante près, qui ne joue pas de rôle dans ce qui suit). Tracez l'allure de

pour

fixés. On distinguera les cas

.
38) Discutez l'évolution de la gouttelette suivant son rayon initial, en distinguant à nouveau les cas

. Quand cela est pertinent, on identifiera une valeur remarquable

, dont on donnera l'expression en fonction des mêmes paramètres qu'à la question 36). On définira également une "énergie d'activation" pour l'apparition de la phase liquide, lorsque l'on part uniquement d'un mélange gazeux air-vapeur d'eau, dont on donnera l'expression en fonction de ces mêmes paramètres.
39) On modélise la phase gazeuse comme un mélange de gaz parfaits. A l'aide de l'expression du potentiel chimique donnée en annexe, que l'on appliquera à la vapeur d'eau, exprimez le rayon critique au-delà duquel une gouttelette croît spontanément en fonction de la "sursaturation"

et de

.
40) A partir de vos connaissances sur la loi d'Arrhénius, ou sur le facteur de Boltzmann, proposez une expression pour la dépendance de la vitesse d'apparition des gouttelettes dans l'atmosphère en fonction de la sursaturation

(cette expression sera obtenue à une constante multiplicative près). Commentez cette dépendance en

On considère la situation représentée sur la figure 5 : une particule solide en suspension dans l'atmosphère présente une cavité conique ouverte sur l'extérieur, de demi-angle d'ouverture

On étudie la possibilité que de l'eau liquide se forme à partir du fond de la cavité, selon la géométrie représentée sur la figure 5. L'eau liquide occupe alors un domaine conique dont la base est un disque de rayon

perpendiculaire à l'axe du cône. Le volume d'un tel cône est

, où

est la hauteur du cône.
41) On fait l'hypothèse que seule l'interface liquide-gaz intervient dans le terme de tension de surface, et donc que l'interface solide-liquide n'engendre aucun terme de tension de surface. Exprimez la différentielle de l'enthalpie libre en fonction de

.
42) Comme à la question 38), identifiez une valeur remarquable de

. Exprimez l'énergie d'activation associée en fonction de

.
43) Expliquez alors pourquoi la présence de particules en suspension dans l'atmosphère favorise l'apparition de nuages.

Quelques rappels

Pour simplifier certaines applications numériques, on donne les racines quatrièmes suivantes :

Thermodynamique générale

Pour un système formé de

constituants (ou phases) de potentiels chimiques

, avec les quantités de matière

, la différentielle de l'énergie interne s'écrit :

et l'enthalpie libre est définie par

. Le dernier terme de la différentielle (6) n'apparaît pas lorsque l'on considère une phase pure ou un système sans transformation de phases (

Thermodynamique des gaz parfaits

On rappelle la relation de Mayer pour un gaz parfait,

, où la constante des gaz parfaits vaut

. Dans un mélange de gaz parfaits, le potentiel chimique

d'un constituant

est donné par la relation :

où

est une fonction qui ne dépend que de la température,

désigne la pression partielle du constituant

, et

bar est une pression de référence.

Masses molaires

On rappelle les masses molaires de l'hydrogène, du carbone, de l'azote et de l'oxygène :