J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

X ENS Physique MP 2013

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo x-ens
🔗 Explorer
Banque
X-ENS
Année
2013
Filière
MP
Matière
Physique
X-ENS MPX-ENS 2013MP PhysiquePhysique 2013
2025_09_04_9adc1a86144ae2d4caddg

COMPOSITION DE PHYSIQUE - (XULC)

(Durée : 4 heures)
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve. On se contentera de donner un unique chiffre significatif aux résultats des applications numériques.

Quelques aspects de l'interaction coulombienne

L'interaction coulombienne joue un rôle important dans de nombreux systèmes physiques et chimiques tels que les plasmas, les gaz d'électrons ou les électrolytes. Nous nous proposons d'en étudier quelques aspects.
Cette étude comprend trois parties. La première introduit la notion de suspension colloïdale. La deuxième aborde les phénomènes d'écrantage électrique et de double couche. Enfin, la troisième traite de l'interaction entre colloïdes.

Données numériques, formulaire et notations

Charge électrique élémentaire : C
Permittivité diélectrique du vide :
Constante de Boltzmann :
Pour
Nombre d'Avogadro :
Masse volumique de l'or ( 300 K ) :
La mobilité d'un ion en solution relie sa vitesse de dérive au champ électrique selon la relation (c'est une grandeur algébrique du même signe que celui de la charge de l'ion).
La permittivité diélectrique d'un milieu s'exprime par la relation , où désigne sa permittivité relative ( ). Dans notre étude, nous admettrons qu'il suffira de remplacer par , dans les formules établies pour le vide.

I Suspension colloïdale et distribution de Maxwell-Boltzmann.

Un milieu fluide, de température uniforme et de masse volumique , contient des particules solides en suspension (que nous appellerons également colloïdes), en régime dilué. Cette solution est soumise au champ de pesanteur . Les colloïdes sont sphériques, de rayon , de volume et de masse . Nous notons leur nombre, par unité de volume, à l'altitude (la grandeur sera appelée concentration).
Pour les ordres de grandeurs, les colloïdes sont en or ( particules ) et le fluide est de l'eau à .
  1. Dans la limite du régime dilué nous admettons que l'équation d'état du gaz colloïdal est celle du gaz parfait. En notant la pression du gaz colloïdal, préciser cette équation en faisant intervenir (et ).
  2. Établir l'équation différentielle traduisant l'équilibre mécanique d'un élément de volume de solution (cette équation fait notamment intervenir et la pression du fluide). Vérifier qu'elle se met sous la forme :
  1. Nous supposons que le fluide est un liquide d'équation d'état Cste et, qu'en régime dilué, il vérifie l'équation de l'hydrostatique, indépendamment de la présence des colloïdes. En déduire l'équation différentielle vérifiée par .
  2. Nous notons . Déterminer et exprimer sa longueur caractéristique de variation, . Calculer .
  3. La relation trouvée est la distribution de Maxwell-Boltzmann. La commenter sur le plan énergétique.
    D'un point de vue statistique, la probabilité élémentaire qu'une particule quelconque se situe dans l'intervalle s'écrit : où est un facteur de proportionnalité. Exprimer en fonction de et , dans le cas d'une solution de hauteur telle que .
  4. Nous convenons que la comparaison du rapport à l'unité définit une frontière entre un état de suspension et celui d'un sédiment. Exprimer, en fonction de et , la taille critique associée à cette frontière. Proposer une interprétation énergétique de ce seuil et justifier le choix du critère adopté. Calculer .
  5. Indiquer à quelle condition, sur et , le gaz de colloïdes peut être effectivement considéré comme un gaz parfait. Est-elle, ici, satisfaite?
  6. La définition de la concentration locale , donnée dans l'introduction, présuppose une uniformité des grandeurs à l'échelle de . Indiquer comment doivent alors se situer la longueur caractéristique et l'extension de l'élément de volume .
  7. Indiquer quelle autre contrainte borne , cette fois inférieurement.
  8. La solution préparée est de concentration initiale homogène. Nous admettons qu'une particule, dans son mouvement au sein du fluide, subit de sa part une force (force de Stokes). désigne la viscosité dynamique du liquide et la vitesse du colloïde par rapport au fluide. Exprimer le temps caractéristique nécessaire à l'obtention du profil d'équilibre de la concentration, dans une solution de hauteur . Estimer pour de l'eau de viscosité et . Quelle conclusion pratique tire-t-on de ce résultat?

II Double couche électrique à la surface d'un colloïde chargé.

Le phénomène de double couche apparaît au voisinage d'une surface chargée, immergée dans un électrolyte. Sous certaines conditions, il se forme une première couche d'ions adsorbés à la surface, suivie d'une seconde couche, dite diffuse, où les ions conservent leur propriété migratoire. Ce phénomène fut découvert au XIX siècle et sa première modélisation est attribuée à Helmholtz (1879). Nous nous proposons de l'étudier au voisinage de la surface d'un colloïde métallique chargé.
L'électrolyte est une solution globalement neutre, de permittivité diélectrique , contenant des cations et des anions de charges respectives et . Cette solution est maintenue à la température .
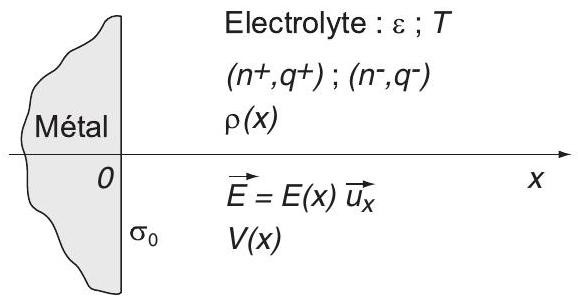
Des colloïdes métalliques sphériques, de rayon , sont dispersés dans cet électrolyte (en régime dilué). Nous supposons que chaque colloïde porte une charge surfacique uniforme, notée l'échelle considérée, la surface d'une telle particule est localement assimilable à un plan infini (figure 1).
Figure 1 - Voisinage immédiat de la surface d'un colloïde métallique chargé.
Nous notons le potentiel et le champ électrique dans la solution, à la distance de la surface du colloїde ( ). La référence de potentiel est fixée par une électrode, plongeant dans la solution loin de la particule (c'est-à-dire où la solution demeure neutre, à l'échelle locale). Nous admettrons que le potentiel est uniforme dans le colloïde ( ).
Les grandeurs et désignent respectivement les concentrations et densités volumiques de courants particulaires, des ions positifs et négatifs, dans la solution. Nous notons et les mobilités (grandeur définie en début de problème), et les coefficients de diffusion, de ces ions en solution. désigne la concentration de chacune des espèces ioniques, loin du colloïde. Nous convenons que l'absence d'exposant (+) ou (-) aux grandeurs ioniques d'une relation signifiera qu'elle se rapporte indifféremment à un cation ou un anion (par exemple " ").
N.B. : Nous ne tenons désormais plus compte de la pesanteur. D'autre part, les concentrations " " qui interviennent se rapportent ici aux ions et non plus aux colloïdes.
Pour les applications numériques nous adopterons:
ions et .

II.A Équations générales.

  1. Nous admettons que le courant particulaire (entendons ou ) est la somme des courants de conduction et de diffusion . Exprimer ce courant en fonction de et .
  2. En régime stationnaire, établir que et sont liés par la relation :
  1. Exprimer l'énergie potentielle électrostatique d'un ion en solution. Nous admettons que la relation (2) coïncide avec la distribution de Maxwell-Boltzmann introduite question (5), mais transposée du domaine gravitationnel au domaine électrostatique. En déduire la relation liant et (relation de Einstein).
    Nous adoptons désormais l'expression de faisant intervenir explicitement .
  2. Exprimer la densité volumique de charge dans la solution. Établir ensuite l'équation différentielle non linéaire (EDV) dont le potentiel est solution.
  3. Nous posons et où et sont respectivement un potentiel et une longueur caractéristiques. Donner les expressions de et pour que l'équation EDV prenne la forme :
Préciser l'intérêt d'une telle écriture.
16. Évaluer et .

II.B Approximation linéaire.

  1. Indiquer à quelle condition l'équation (3) tend vers une équation linéaire que l'on précisera. C'est cette forme approchée que nous adopterons dans cette partie.
  2. Exprimer et en faisant intervenir .
  3. Esquisser la représentation graphique de (on supposera ). Interpréter ce tracé en comparant cette situation à celle pour laquelle l'électrolyte serait remplacé par le vide. Commenter la dépendance de avec la température. Quelle approximation le rapport , calculé question (16), permet-il de contrôler?
  4. Exprimer la capacité d'un colloïde de surface d'aire ( où est la charge du colloïde et son potentiel). Commenter ce résultat.
  5. Évaluer (exprimée en Å ) pour . Préciser l'intérêt de ce choix d'unité. Commenter ce résultat.

II.C Solution générale.

Nous considérons ici l'équation (3) dans le cadre général. Nous notons le champ électrique adimensionnalisé.
22. Expliciter le champ caractéristique . Indiquer pourquoi ce résultat pouvait être attendu (à un préfacteur numérique près).
23. En déterminant l'intégrale première associée à l'équation (3), établir que s'écrit (on supposera ) :
  1. Exprimer la densité volumique de charge , dans la solution, en fonction de . Interpréter son signe.
  2. Exprimer la charge surfacique du colloïde, en fonction de .
  3. Déterminer la capacité d'un colloïde de surface d'aire , en fonction de ( est définie question ( )).
  4. Exprimer la charge totale , de la solution, enrobant le colloïde, ramenée à l'unité de surface de ce dernier. Commenter la comparaison de à . La solution demeure-t-elle globalement neutre? Pourquoi?
  5. L'intégration de l'équation (4), conduit à l'expression du potentiel (Gouy 1910, Chapman 1913) :
ù
Vérifier la compatibilité, avec cette expression générale, de la relation correspondante établie dans le cadre linéaire.
29. La figure (2) représente la dépendance spatiale de obtenue par ce modèle (voir légende). Analyser cette évolution en considérant que les ions ont une taille de l'ordre de l'angström.
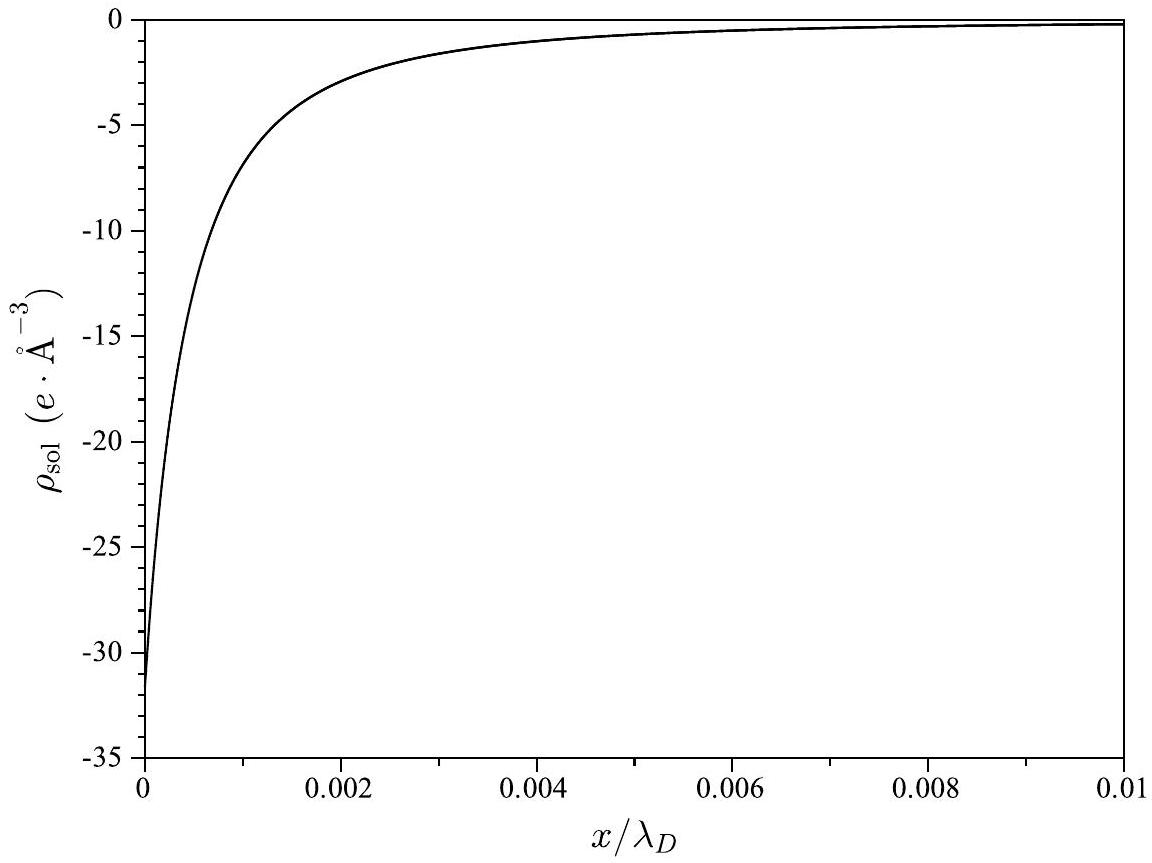
Figure 2 - Dépendance spatiale de Å calculée pour , Å.
  1. En s'appuyant sur la figure (2), justifier qu'il se forme, près de la surface du colloïde, une couche compacte d'ions, précédant une seconde couche, dite diffuse, où les ions conservent leur mobilité (il s'agit du phénomène de double couche évoqué en introduction).
  2. Ce modèle donne les résultats suivants :
  • Pour Å et Å;
  • Pour Å et Å.
En déduire l'ordre de grandeur de l'épaisseur de la couche compacte, pour . Préciser à combien de couches d'ions adsorbés elle correspond.
32. L'hypothèse implicitement adoptée qui a conduit à considérer l'électrolyte comme un milieu continu est-elle vérifiée dans la situation illustrée figure (2) ?

III Quelques aspects de l'interaction entre colloïdes.

Nous considérons deux colloïdes (1) et (2) situés à une distance telle que l'on ne peut plus négliger leur influence réciproque. À l'échelle de notre étude nous considérons toujours que la géométrie sphérique peut être, localement, approchée par une géométrie plane et notons l'aire de leur surface effective d'interaction. Nous notons le vecteur distance (orienté de 1 vers 2) entre les deux surface des colloïdes. Nous souhaitons exprimer la force d'interaction, de (1) sur (2), . Ces colloïdes sont connectés à un générateur imposant leur potentiel (relativement à une électrode de référence). Chaque colloïde porte alors la densité surfacique de charge et la charge . Enfin, un opérateur mécanique exerce sur (2) la force , nécessaire au maintien de l'équilibre mécanique des colloïdes ((1) étant supposé immobilisé par un autre opérateur mécanique).
33. Donner les allures de et entre les colloïdes ( ), pour .
34. Nous considérons le système thermodynamique constitué des deux surfaces (1) et (2) et de l'électrolyte compris entre ces deux surfaces. Nous notons sa température et son entropie.
a) Exprimer le travail élémentaire fourni par le générateur et l'opérateur mécanique lors d'une transformation élémentaire réversible .
b) En déduire l'expression de la différentielle de l'énergie interne du système.
c) Déduire de cette différentielle celle de la fonction d'état dont les variables sont et (nous notons cette fonction d'état).
d) Nous considérons la variation , de la fonction , entre les états initial et final . En empruntant, dans le plan isotherme ( ), deux chemins bien choisis que l'on décrira, établir l'égalité :
Donner l'expression de .
e) Exprimer sous forme intégrale (que l'on ne cherchera pas à expliciter). Préciser son signe.
35. Parallèlement à l'interaction électrostatique due à la charge des colloïdes, ceux-ci sont également soumis à une interaction due aux forces de van der Waals (conséquence des interactions dipôle-dipôle des atomes formant les colloïdes). Celle-ci est attractive, faible, variant avec la distance comme , mais n'est pas écrantée. En admettant que varie comme , expliquer pourquoi la suspension colloïdale est susceptible de former des agrégats, lorsque la concentration ionique augmente.
36. Nous supposons que des agrégats se forment à partir de colloïdes identiques (sphériques de rayon portant tous la même charge . En considérant que les agrégats sont sphériques et compacts, exprimer la charge surfacique d'un agrégat formé de colloïdes.
Dans le cadre de ce modèle, et en ne considérant que le seul effet de la charge, le processus d'agrégation est-il favorisé par leur croissance?
37. Nous supposons que la condition d'agrégation est satisfaite. Discuter les grandeurs (ou paramètres) influençant la cinétique d'agrégation.
X ENS Physique MP 2013 - Version Web LaTeX | WikiPrépa | WikiPrépa