Le neutrino est un type de particule élémentaire électriquement neutre dont il existe trois espèces appelées "saveurs". En 1957, le physicien Bruno Pontecorvo a imaginé qu'un neutrino peut changer de saveur au cours du temps. Ce phénomène, appelé "oscillation des neutrinos", a été confirmé en 1998, et cette découverte a été récompensée par le prix Nobel de physique en 2015. L'oscillation a été observée grâce au détecteur Super-Kamiokande, immense cylindre rempli d'eau situé au Japon. Les neutrinos sont détectés lorsqu'ils entrent en collision avec une molécule d'eau du détecteur. Un électron est alors produit, et éjecté à une vitesse supérieure à celle de la lumière dans l'eau. Il produit alors une lumière via un mécanisme nommé "effet Tcherenkov", qui est captée par des photomultiplicateurs disposés sur toute la surface du détecteur. Le but de ce problème est d'étudier le phénomène quantique d'oscillation des neutrinos et l'effet Tcherenkov qui permet leur observation.

Les parties I, II.1, II. 2 et II. 3 peuvent être résolues indépendamment pour l'essentiel.

I. Oscillation de neutrinos

Dans cette partie, nous nous intéressons à deux des trois saveurs de neutrinos, dites électronique et muonique, notées respectivement

. Lors du phénomène d'oscillation de neutrinos, le neutrino électronique a une certaine probabilité de changer de saveur et de devenir un neutrino muonique (et réciproquement). Pour étudier ce phénomène, nous allons exploiter une analogie avec la molécule d'ammoniac (

), dans laquelle l'atome d'azote oscille de gauche à droite du plan formé par les trois atomes d'hydrogène. On repère par la coordonnée cartésienne

la position de l'atome d'azote sur l'axe perpendiculaire à ce plan.

Quelle est l'origine physique de l'oscillation de l'atome d'azote?
On note et les fonctions d'onde correspondant aux deux positions possibles de l'atome d'azote. D'après le principe de superposition, l'état physique de l'ammoniac s'écrit comme combinaison linéaire de ces deux fonctions d'onde : . Donnez l'interprétation des coefficients et et écrivez la relation qui les lie.
Les états et ne sont pas des états stationnaires de l'équation de Schrödinger qui décrit l'évolution de la molécule d'ammoniac. On désigne par et ces états stationnaires donnés par . On place l'atome d'azote dans un de ces états stationnaires. Comment sa fonction d'onde évolue-t-elle dans le temps?
À l'instant , la molécule d'ammoniac est préparée dans l'état . Déterminez l'expression du coefficient .
Exprimez la probabilité que l'atome d'azote soit détecté à gauche du plan formé par les atomes d'hydrogène en fonction de la différence d'énergie des états stationnaires. Tracez l'évolution temporelle de et donnez sa période.
L'oscillation des neutrinos est analogue à celle de l'atome d'azote de la molécule d'ammoniac. Au lieu d'être une oscillation spatiale, elle se produit dans l'espace abstrait des saveurs dans lequel les états et correspondent respectivement aux états et . Dans cette analogie, l'équivalent des états stationnaires sont des états dont les énergies de masse et sont beaucoup plus petites que les autres énergies mises en jeu. Les neutrinos voyagent alors à des vitesses très proches de celle de la lumière dans le vide, situation dans laquelle les lois de la mécanique newtonienne ne s'appliquent plus. On admet alors que l'énergie totale et la quantité de mouvement sont liées par . Écrivez en fonction de et dans la limite où .
En déduire l'expression donnant la différence d'énergie pour deux neutrinos de même quantité de mouvement , en fonction de et de la quantité .
On s'intéresse aux neutrinos produits par les réacteurs des centrales nucléaires, qui sont des neutrinos électroniques. On note la distance parcourue par un neutrino pendant la durée . Montrez que la probabilité pour le neutrino d'être dans l'état après la distance , notée , est périodique. Exprimez sa période spatiale d'oscillation en fonction de et de .

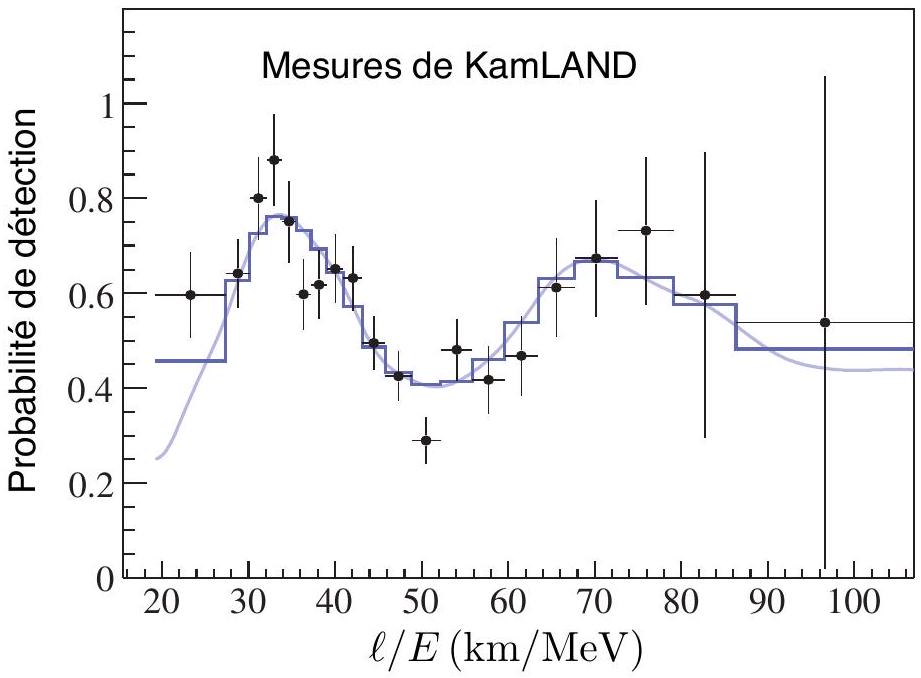
Figure 1 - Probabilité de détection d'un neutrino électronique en fonction de

, où

est la distance moyenne entre les réacteurs nucléaires, sources de neutrinos, et le détecteur;

est l'énergie du neutrino. La courbe bleue constante par morceaux est l'ajustement aux données représentées par des points avec leurs barres d'erreur.

En 2002, la collaboration KamLAND, utilisant le détecteur Super-Kamiokande, a recueilli les neutrinos électroniques issus de tous les réacteurs nucléaires du Japon, ce qui revient à prendre une distance moyenne . Le résultat de ce travail est présenté sur la figure 1 . Estimez la valeur de à partir de ces données.

Donnée numérique :

.
10. Le détecteur mesure le flux de neutrinos avec une précision de l'ordre de

. À quelle distance minimale

placeriez-vous le détecteur pour observer l'amorce du phénomène d'oscillation des neutrinos?
11. D'autres expériences de détection de neutrinos issus de centrales nucléaires ont été réalisées, notamment auprès du réacteur franco-belge de Chooz dans les Ardennes et du réacteur du Bugey dans l'Ain. Leurs résultats sont indiqués sur la figure 2. Expliquez ces résultats en considérant des neutrinos d'énergie

.
12. Les neutrinos issus des réactions se déroulant au coeur du Soleil se propagent sur une distance de 150 millions de kilomètres avant d'atteindre le détecteur et leur distribution en énergie est centrée autour de 4 MeV . À quelle valeur moyenne de

doit-on s'attendre pour ceux-ci?

II. Effet Tcherenkov

Lorsqu'une particule chargée se déplace dans un milieu transparent avec une vitesse supérieure à la vitesse de la lumière dans ce milieu, elle émet une lumière appelée "rayonnement Tcherenkov", du nom du physicien russe ayant étudié ce phénomène. Il est fréquemment utilisé pour la détection

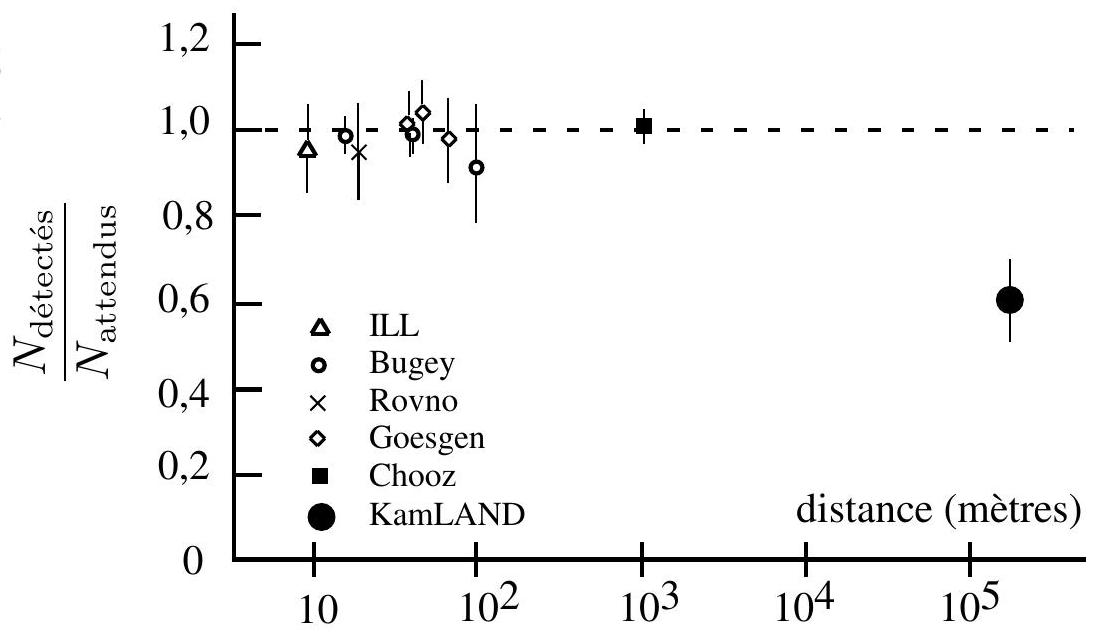
Figure 2 - Rapport entre les nombres de neutrinos électroniques détectés et attendus en l'absence d'oscillations, en fonction de la distance

au réacteur, pour différentes expériences.

des particules chargées rapides. Il a joué un rôle crucial dans l'observation des oscillations de neutrinos. Cette partie étudie quelques caractéristiques du rayonnement Tcherenkov.

II.1. Répartition spatiale du rayonnement Tcherenkov

Soit une particule chargée en mouvement rectiligne uniforme à la vitesse dans un milieu transparent. On admet qu'elle émet en chaque point de sa trajectoire une onde électromagnétique sphérique se propageant à la vitesse , qu'on suppose indépendante de la longueur d'onde. On modélise dans un premier temps la propagation de cette onde dans l'approximation de l'optique géométrique. Montrez que si , l'onde occupe l'intérieur d'un cône dont vous préciserez l'axe et le demi-angle au sommet , et que vous représenterez sur un schéma.
On considère maintenant le cas où la particule émet en chaque point de sa trajectoire un signal de pulsation . Un observateur immobile situé à l'infini, dans une direction faisant un angle avec la vitesse de la particule chargée, reçoit ce signal de pulsation . Déterminez à quelle condition sur les signaux émis en deux points différents de la trajectoire arrivent en phase au point d'observation.
Qu'en déduisez-vous sur la direction du rayonnement émis? Quel est l'angle entre cette direction et la surface du cône de la question 13 ? Quel résultat général retrouve-t-on?
Le détecteur Super-Kamiokande est un observatoire de neutrinos situé au Japon. Il consiste en un cylindre de révolution d'axe vertical, de 39 mètres de haut et 42 mètres de diamètre, entièrement rempli d'eau. Les neutrinos sont détectés lorsqu'ils entrent en collision avec une molécule d'eau du détecteur. Un électron est alors éjecté en ligne droite à une vitesse très voisine de la vitesse de la lumière dans le vide, . Il émet alors du rayonnement Tcherenkov sur une certaine distance, avant d'être freiné par l'eau. L'indice de réfraction de l'eau vaut . Estimez l'angle entre la direction de l'électron et la direction de la lumière Tcherenkov. La calculatrice n'étant pas autorisée, vous vous contenterez de situer cet angle par rapport aux angles de référence .
La figure 3 représente l'intensité de la lumière Tcherenkov émise par un électron, ainsi que l'instant où elle est reçue, en chaque point de la surface du détecteur. Expliquez sans calcul comment ces données permettent de localiser le point du détecteur où le neutrino est entré en collision avec une molécule d'eau, ainsi que la direction de l'électron éjecté. Vous préciserez en

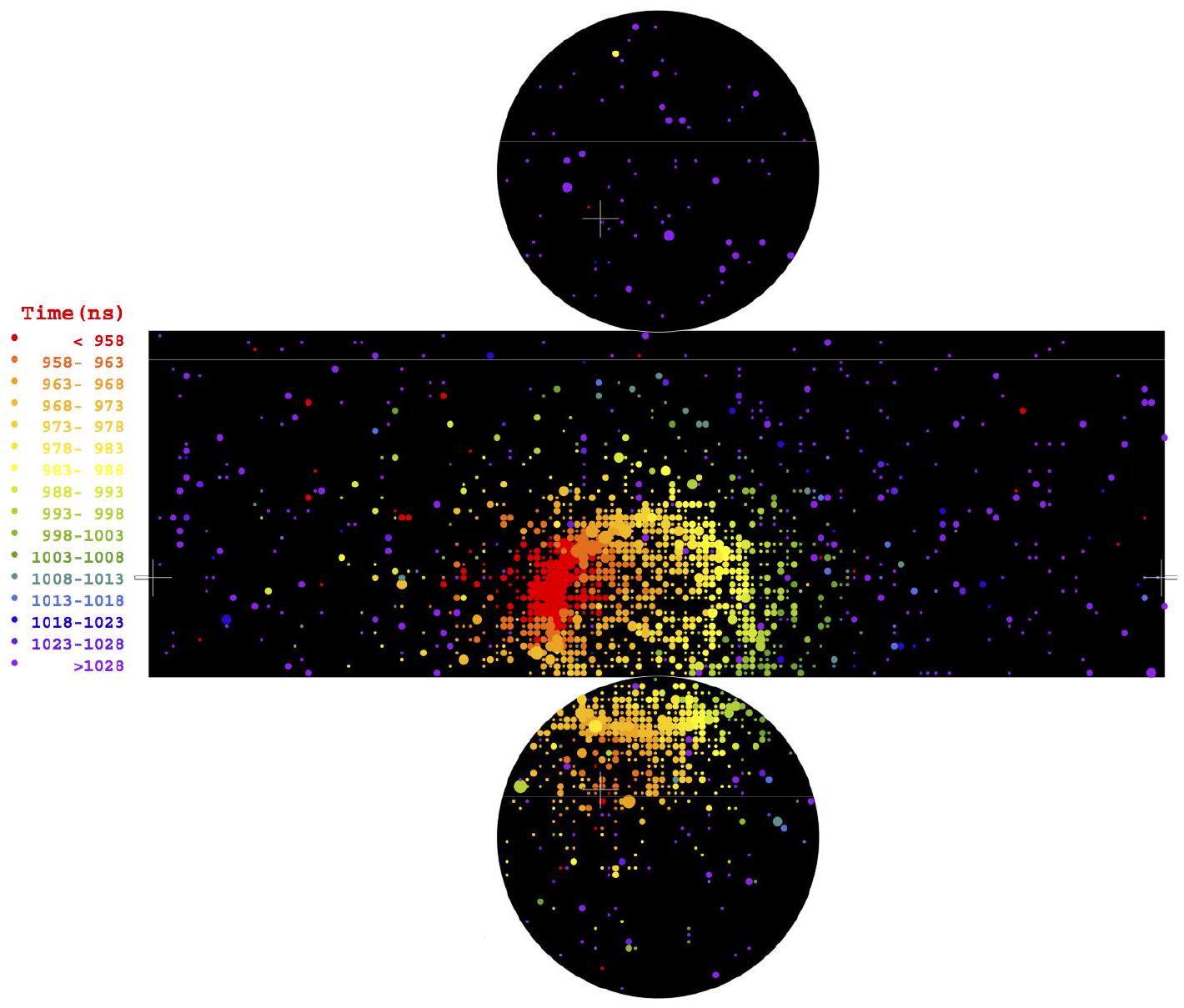
Figure 3 - Rayonnement Tcherenkov produit par un électron, et détecté par Super-Kamiokande. Les photomultiplicateurs sont répartis sur toute la surface du cylindre. Les deux disques correspondent au couvercle et au fond du cylindre, et le rectangle allongé à sa surface latérale qui a été dépliée pour permettre une représentation plane. Les points colorés sont ceux où la lumière est observée, et on a choisi des couleurs différentes suivant les temps d'arrivée de la lumière, comptés à partir d'une origine arbitraire.

particulier les rôles de la taille et de la forme de la tache lumineuse, ainsi que celui des temps d'arrivée. Vous commenterez les écarts entre ces derniers.
18. L'effet Tcherenkov est également utilisé dans certaines expériences de physique des particules élémentaires pour mesurer la vitesse des particules chargées rapides. La figure 4 représente l'angle entre la lumière Tcherenkov et la direction de la vitesse des particules, en fonction de la quantité de mouvement de ces particules, pour des particules de différentes masses, repérées par les lettres

. On admet que lorsque la quantité de mouvement tend vers l'infini, la vitesse tend vers la vitesse de la lumière dans le vide

, pour chacune de ces particules. Évaluez, à partir des données de la figure, la valeur numérique de l'indice optique du milieu,

, utilisé dans ce détecteur. Vous évaluerez plus précisément la différence

, et vous comparerez avec sa valeur dans l'eau et dans l'air. Quelle est la vitesse minimale que doit avoir une particule pour que son passage produise l'effet Tcherenkov dans ce détecteur?

II.2. Spectre du rayonnement Tcherenkov

On note la puissance du rayonnement Tcherenkov dans un petit intervalle de pulsation de largeur autour de est donc la puissance rayonnée par unité de pulsation. Dans

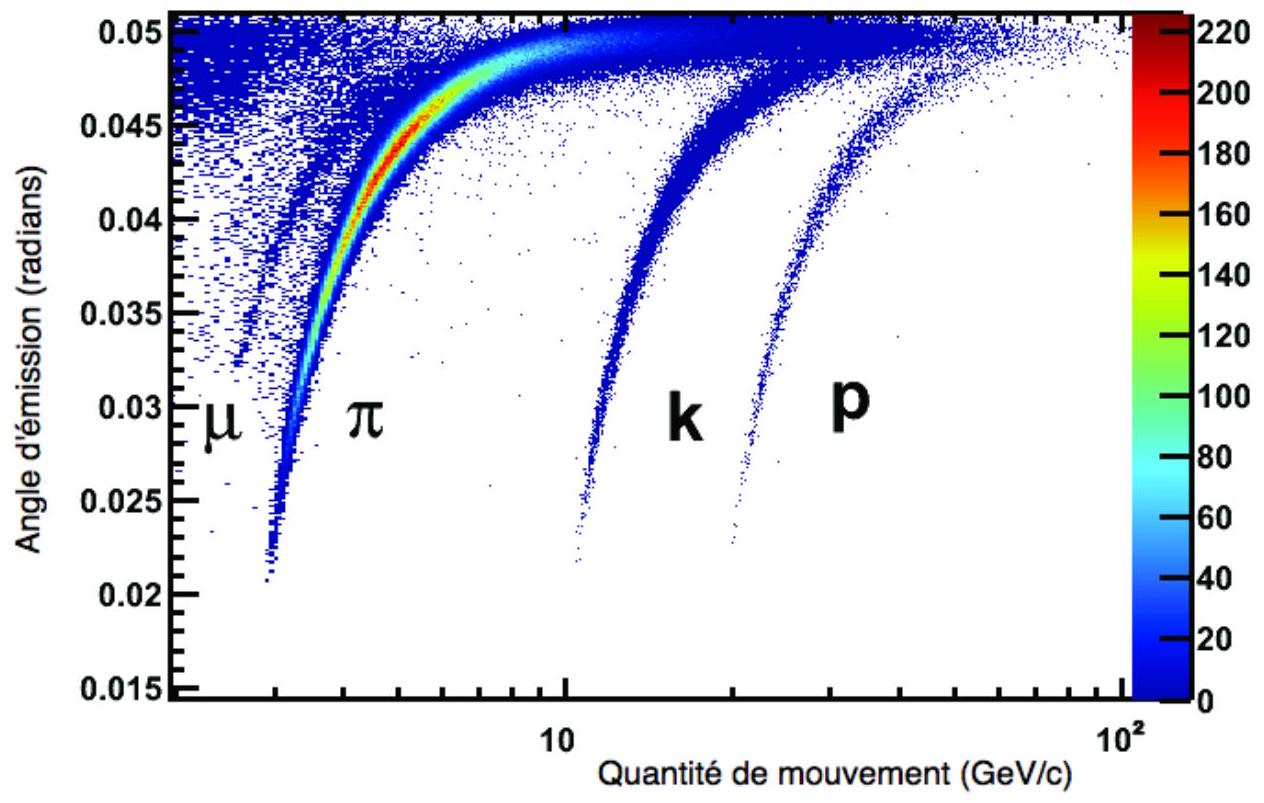
Figure 4 - Données issues du détecteur Tcherenkov de l'expérience LHCb, au laboratoire CERN (Genève). On mesure, pour chaque particule arrivant dans le détecteur, sa quantité de mouvement (au moyen d'un champ magnétique) et l'angle d'émission de la lumière Tcherenkov, déterminé à la question 15. Chaque point est une mesure. Leur dispersion résulte de l'incertitude associée à chacune d'elles. On ne tiendra pas compte de l'échelle des couleurs.

les questions 19 à 22, on se place dans la limite où la vitesse

de la particule chargée est proche de la vitesse de la lumière dans le vide,

. On suppose que

ne dépend alors que de

(charge électrique de la particule),

, et des constantes fondamentales

(permittivité diélectrique du vide). Déterminez par analyse dimensionnelle la forme de cette dépendance.
20. En déduire la forme de la puissance rayonnée par unité de longueur d'onde dans le vide

. Tracez l'allure de sa variation en fonction de

. Pour donner un élément de comparaison, la figure 5 représente la variation de la puissance rayonnée par unité de longueur d'onde pour le rayonnement solaire. De quelle couleur le rayonnement Tcherenkov apparaît-il à nos yeux?
21. Montrez comment on obtient, à partir de la puissance rayonnée par unité de longueur d'onde, le nombre de photons rayonnés entre les longueurs d'onde

lorsque la particule parcourt une distance

.
22. L'analyse dimensionnelle faite à la question 19 ne permet de déterminer la puissance rayonnée qu'à un facteur près, dont on sait juste qu'il est sans dimension. Nous faisons maintenant l'hypothèse supplémentaire que ce facteur adimensionné est d'ordre 1, ce qui permet d'obtenir un ordre de grandeur du résultat. Le détecteur Tcherenkov de l'expérience LHCb a une épaisseur de 5 cm . Quel est l'ordre de grandeur du nombre de photons rayonnés dans le domaine visible par un électron de charge

traversant ce détecteur sous incidence normale?

Donnée numérique :

II.3. Polarisation du rayonnement Tcherenkov

La modélisation théorique complète du rayonnement Tcherenkov fait appel aux équations de Maxwell dans un milieu d'indice réel. La source du rayonnement est la densité de courant

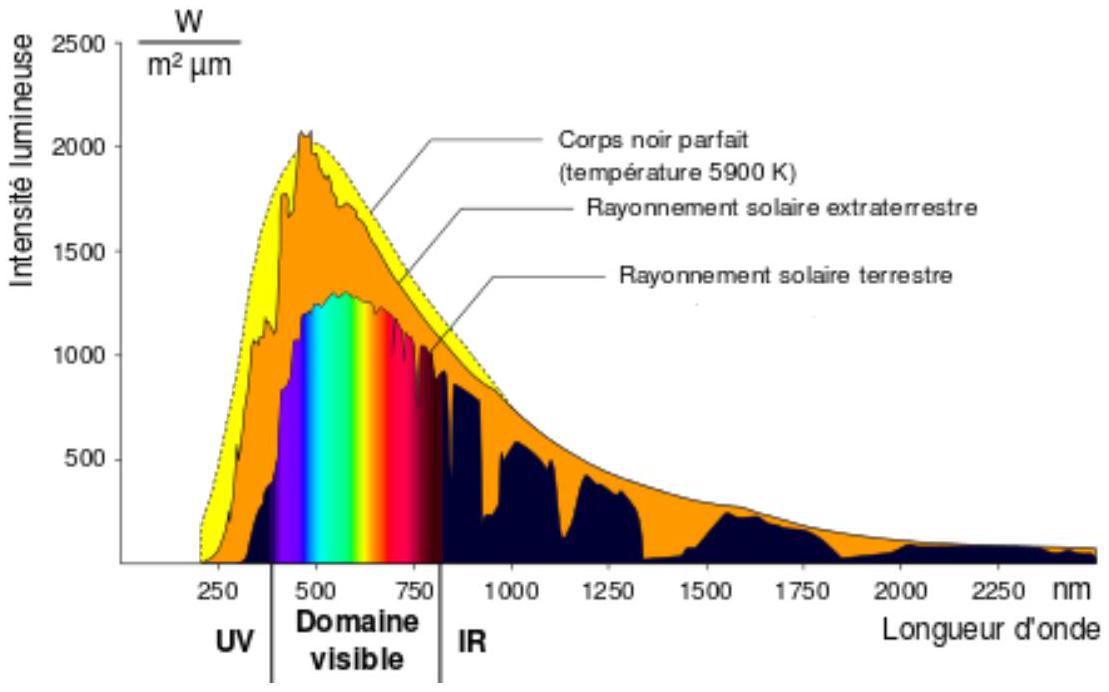
Figure 5 - Puissance lumineuse reçue du Soleil sous incidence normale par unité de surface et de longueur d'onde. On s'intéresse au rayonnement solaire terrestre. Les deux autres courbes sont données à titre indicatif.

associée au mouvement rectiligne uniforme de la particule chargée à la vitesse

. De quelle combinaison de

dépend-elle?
24. On s'intéresse à une composante de Fourier du champ électromagnétique proportionnelle à

, qui sera créée par la composante de Fourier du courant elle-même proportionnelle à

. Déduisez du résultat de la question précédente une relation entre

.
25. Quelle est par ailleurs, sans démonstration, la relation entre

pour l'onde rayonnée dans le milieu?
26. À partir des résultats des questions 24 et 25 , retrouvez l'expression de l'angle entre le rayonnement Tcherenkov et la direction de la particule chargée.
27. Soit une composante de Fourier du champ rayonné proportionnelle à

. Déterminez les directions du champ électrique et du champ magnétique de cette composante par un argument de symétrie. Que peut-on dire de la polarisation du rayonnement Tcherenkov?
28. Quel est le phénomène analogue à l'effet Tcherenkov en acoustique? Quelle différence, liée à la polarisation, voyez-vous entre eux lorsque

est proche de la vitesse de la lumière dans le milieu