Version interactive avec LaTeX compilé
ÉCOLE POLYTECHNIQUE - ÉCOLES NORMALES SUPÉRIEURES ÉCOLE SUPÉRIEURE DE PHYSIQUE ET DE CHIMIE INDUSTRIELLES
COMPOSITION DE PHYSIQUE - B - (XEULC)
(Durée : 4 heures)
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
On se contentera, pour les applications numériques, d'un seul chiffre significatif.
Les deux problèmes sont indépendants.
On se contentera, pour les applications numériques, d'un seul chiffre significatif.
Les deux problèmes sont indépendants.
I. Trajectoire d'un volant de badminton
Le badminton est un sport dans lequel les joueurs frappent un projectile, appelé volant, à l'aide d'une raquette. Le but de ce problème est de proposer une modélisation simplifiée de la trajectoire du volant sous l'effet conjugué de la pesanteur et de la résistance de l'air, et de confronter le modèle aux résultats d'une expérience. On négligera la poussée d'Archimède dans tout le problème.
On néglige dans un premier temps la force de freinage exercée par l'air.
I. 1 On lance depuis le sol le volant de masse
I. 2 Validez dimensionnellement l'expression de
I. 3 La vitesse initiale étant fixée, quel angle
I. 1 On lance depuis le sol le volant de masse
I. 2 Validez dimensionnellement l'expression de
I. 3 La vitesse initiale étant fixée, quel angle
On tient maintenant compte du freinage de l'air, modélisé en assimilant le volant à une sphère solide en mouvement dans un fluide newtonien. On écrit la force de freinage sous la forme
I. 4 Déterminer la dimension de
I. 5 La viscosité cinématique de l'air est
I. 6 Écrire l'équation du mouvement du volant. Montrer qu'elle admet une solution particulière, correspondant à un mouvement rectiligne uniforme dont on exprimera la vitesse, notée
I. 7 Récrire l'équation du mouvement en faisant notamment apparaître le rapport
I. 8 À quelle condition sur
I. 9 En utilisant cette expression, déterminer et calculer le temps
I. 10 Toujours dans le cadre de l'approximation de la question I.8, déterminer l'expression donnant la distance horizontale
I. 11 Obtenir
I. 12 On suppose que l'approximation de la question I. 8 cesse d'être valable lorsque la composante verticale de la force de freinage est égale au poids. Quelle est l'expression de
I. 4 Déterminer la dimension de
I. 5 La viscosité cinématique de l'air est
I. 6 Écrire l'équation du mouvement du volant. Montrer qu'elle admet une solution particulière, correspondant à un mouvement rectiligne uniforme dont on exprimera la vitesse, notée
I. 7 Récrire l'équation du mouvement en faisant notamment apparaître le rapport
I. 8 À quelle condition sur
I. 9 En utilisant cette expression, déterminer et calculer le temps
I. 10 Toujours dans le cadre de l'approximation de la question I.8, déterminer l'expression donnant la distance horizontale
I. 11 Obtenir
I. 12 On suppose que l'approximation de la question I. 8 cesse d'être valable lorsque la composante verticale de la force de freinage est égale au poids. Quelle est l'expression de
On modélise la trajectoire du
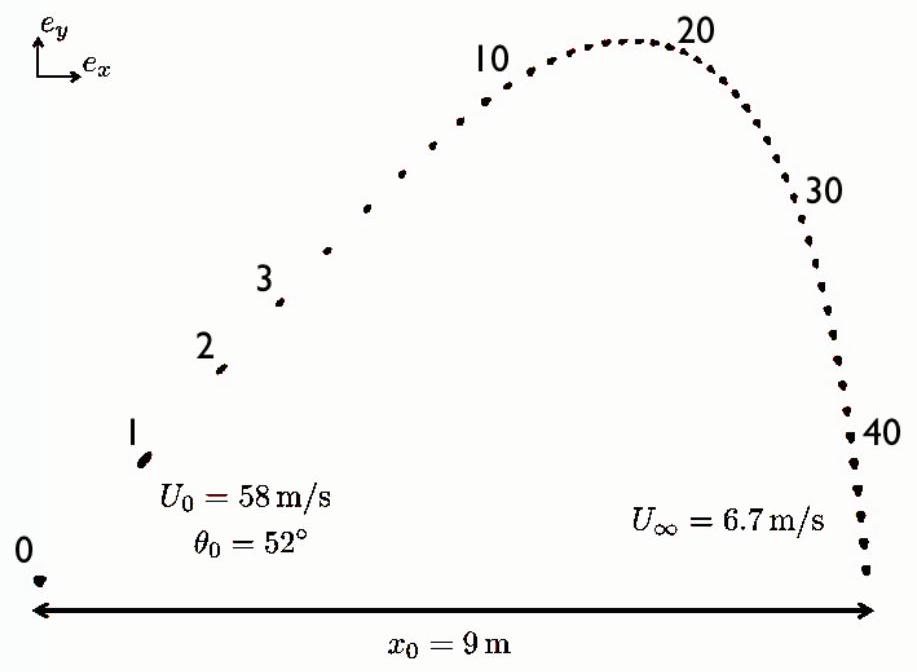
Figure 1: Positions successives d'un volant de badminton allant de la gauche vers la droite, enregistrées toutes les 50 ms . Le premier point, repéré par le chiffre 0 , correspond au lancer à
volant en distinguant trois régimes successifs : (1) le régime que l'on vient d'étudier, durant lequel l'accélération de la pesanteur est négligeable ; (2) un régime intermédiaire ; (3) un régime limite durant lequel l'accélération du volant est négligeable.
I. 13 Localiser sur la chronophotographie le régime limite ainsi défini, en justifiant précisément votre réponse.
I. 14 Une approximation de la trajectoire consiste à oublier la partie correspondant au régime intermédiaire. Dessiner la trajectoire obtenue dans cette approximation.
I. 15 Donner l'expression littérale de la portée du tir dans cette approximation. Comment se compare-t-elle à la portée en l'absence de freinage, déterminée à la question I. 1 ?
I. 16 Estimer numériquement la portée du tir. On donne
I. 17 Durant le régime intermédiaire, tous les termes de l'équation du mouvement sont du même
ordre de grandeur. En déduire, par un argument dimensionnel, une expression littérale de l'ordre de grandeur de la distance parcourue lors du régime intermédiaire. Dans quelle limite l'approximation faite à la question I. 14 est-elle justifiée ?
I. 18 Comment faudrait-il modifier les paramètres de l'expérience pour que la trajectoire corresponde plus précisément à celle obtenue à la question I. 14 ? On discutera suivant la vitesse initiale et la nature du projectile. La convergence vers cette solution limite est-elle plutôt rapide, ou lente?
I. 19 Donner les expressions littérales des temps de montée et de descente du volant. Estimer, par un argument dimensionnel, l'ordre de grandeur littéral de la durée du régime intermédiaire. Comparer les durées de ces trois régimes dans la limite où l'approximation de la question I. 14 s'applique.
I. 13 Localiser sur la chronophotographie le régime limite ainsi défini, en justifiant précisément votre réponse.
I. 14 Une approximation de la trajectoire consiste à oublier la partie correspondant au régime intermédiaire. Dessiner la trajectoire obtenue dans cette approximation.
I. 15 Donner l'expression littérale de la portée du tir dans cette approximation. Comment se compare-t-elle à la portée en l'absence de freinage, déterminée à la question I. 1 ?
I. 16 Estimer numériquement la portée du tir. On donne
I. 17 Durant le régime intermédiaire, tous les termes de l'équation du mouvement sont du même
ordre de grandeur. En déduire, par un argument dimensionnel, une expression littérale de l'ordre de grandeur de la distance parcourue lors du régime intermédiaire. Dans quelle limite l'approximation faite à la question I. 14 est-elle justifiée ?
I. 18 Comment faudrait-il modifier les paramètres de l'expérience pour que la trajectoire corresponde plus précisément à celle obtenue à la question I. 14 ? On discutera suivant la vitesse initiale et la nature du projectile. La convergence vers cette solution limite est-elle plutôt rapide, ou lente?
I. 19 Donner les expressions littérales des temps de montée et de descente du volant. Estimer, par un argument dimensionnel, l'ordre de grandeur littéral de la durée du régime intermédiaire. Comparer les durées de ces trois régimes dans la limite où l'approximation de la question I. 14 s'applique.
II. Mesure de la masse du photon
La théorie actuelle de l'électromagnétisme est constituée par les équations de Maxwell, qui sont compatibles avec toutes les expériences réalisées. On ne peut néanmoins exclure la possibilité que des expériences plus précises mettent un jour cette théorie en défaut, auquel cas il faudrait la modifier. Le but de ce problème est de proposer une modification des équations de Maxwell, et de confronter cette nouvelle théorie à deux expériences.
A. Modification des équations de Maxwell
II. 1 On suppose que le champ électrique dans le vide satisfait à l'équation
où
II. 2 Exprimer la vitesse de groupe
II. 3 Soit un champ
II. 2 Exprimer la vitesse de groupe
II. 3 Soit un champ
B. Mesure astrophysique
Un pulsar est un astre tournant très rapidement sur lui-même (avec une période souvent inférieure à la seconde) et émettant un fort rayonnement électromagnétique dans un cône étroit centré autour de son axe magnétique, qui est distinct de son axe de rotation. On observe ainsi sur Terre un signal lumineux sous forme d'impulsions périodiques en provenance de cet astre, d'où le nom de "pulsar".
II. 4 On enregistre ce signal séparément dans deux domaines de longueur d'onde différents, en fonction du temps. Expliquer sans calcul comment se traduirait, sur ces mesures, une petite dispersion de la lumière en fonction de la longueur d'onde.
II. 5 On note
II. 6 Des observations des lumières bleue et rouge en provenance du pulsar de la nébuleuse du Crabe n'ont pas permis de déceler de dispersion. Calculer numériquement la borne supérieure sur
II. 4 On enregistre ce signal séparément dans deux domaines de longueur d'onde différents, en fonction du temps. Expliquer sans calcul comment se traduirait, sur ces mesures, une petite dispersion de la lumière en fonction de la longueur d'onde.
II. 5 On note
II. 6 Des observations des lumières bleue et rouge en provenance du pulsar de la nébuleuse du Crabe n'ont pas permis de déceler de dispersion. Calculer numériquement la borne supérieure sur
Données numériques :
II. 7 En déduire un ordre de grandeur de la borne supérieure sur
II. 8 Quel est l'intérêt, pour cette analyse, d'avoir recours à des objets astrophysiques ? Quel domaine de longueur d'onde faudrait-il observer pour améliorer la borne supérieure obtenue ?
II. 7 En déduire un ordre de grandeur de la borne supérieure sur
II. 8 Quel est l'intérêt, pour cette analyse, d'avoir recours à des objets astrophysiques ? Quel domaine de longueur d'onde faudrait-il observer pour améliorer la borne supérieure obtenue ?
C. Une expérience d'électrostatique
II. 9 On se place, dans toute cette partie, dans le cadre de l'électrostatique. On admet que l'équation de Maxwell-Gauss est modifiée comme suit :
où
II. 10 Une sphère métallique creuse parfaitement conductrice, de rayon
II.11 On cherche à déterminer comment une valeur non nulle de
II.12 Préciser le domaine de validité de l'approximation faite à la question précédente, sous forme d'une condition sur
II.13 On essaie de déceler une valeur non nulle de
II. 10 Une sphère métallique creuse parfaitement conductrice, de rayon
II.11 On cherche à déterminer comment une valeur non nulle de
II.12 Préciser le domaine de validité de l'approximation faite à la question précédente, sous forme d'une condition sur
II.13 On essaie de déceler une valeur non nulle de
