De nombreuses situations expérimentales, en particulier en robotique, requièrent une mesure de distances et de vitesses d'une manière relativement simple et aussi peu coûteuse que possible. Le but de ce problème est de montrer comment cet objectif peut être atteint à l'aide d'une diode laser, source de lumière que l'on supposera monochromatique et dont la fréquence peut être légèrement modifiée par un courant de commande.

I - Diode laser

Dans tout le problème, la diode est constituée par un milieu homogène, transparent, d'indice

, limité par des faces planes et parallèles distantes de

; elle est placée dans le vide (figure 1). Entre ces faces formant cavité, l'onde optique est constituée de deux ondes progressives, supposées planes, se propageant en sens inverse, perpendiculairement aux faces; la direction commune de propagation sera choisie comme axe

. Polarisée linéairement, chaque onde sera représentée par l'amplitude complexe

du champ électrique dont la dépendance

Figure 1

temporelle est de la forme

En utilisant les relations de continuité du champ électromagnétique, déterminer le coefficient de réflexion en amplitude sur une face de la cavité (milieu vide) en fonction de ainsi que le coefficient de transmission correspondant.
Soit l'amplitude complexe, au niveau de la face 2 (figure 1), de l'onde qui arrive sur cette face. On désigne par le module du vecteur d'onde dans le vide. Exprimer l'amplitude de l'onde après un aller et retour complet dans la cavité en fonction de et .
En fait, au cours de son trajet dans la cavité, l'onde est amplifiée par le phénomène appelé émission induite. Une manière d'exprimer cette propriété est d'utiliser un indice complexe tel que avec .
a) Justifier la forme de cette expression.
b) Trouver la relation qui doit exister entre et pour qu'il y ait un régime permanent d'amplitude constante. Cette relation sera dans la suite dénommée «condition laser ».
On suppose , ce qui permet d'utiliser pour l'expression obtenue en 1. En régime permanent, la diode laser n'émet que pour des fréquences particulières situées dans une certaine plage.
a) Déterminer l'écart entre deux fréquences consécutives possibles et de l'onde.
b) On appelle «coefficient d'amplification » le facteur . Déterminer en fonction de et la valeur que doit avoir en régime permanent?
Application numérique. On donne et .
a) Calculer et .
b) La longueur d'onde de l'oscillation laser est voisine de 845 nm ; calculer la valeur de correspondante; justifier l'approximation faite sur la valeur de à la question 4.
L'amplification dans un milieu laser nécessite une «inversion de populations », c'est-à-dire que le niveau supérieur de la transition optique soit plus peuplé que le niveau inférieur. L'émission induite tend à diminuer cette inversion, ce qui entraîne que le coefficient d'amplification décroît lorsque l'intensité de l'onde optique croît ; l'intensité est définie ici comme la puissance de chaque onde progressive à l'intérieur de la cavité. On admettra que la relation entre et est de la forme : où et sont deux constantes. On donne , .

Calculer

en régime permanent et la puissance de sortie

du faisceau laser par l'une des faces.

II - Principe des mesures de position et de vitesse d'un obstacle

Dans cette partie, on étudie qualitativement l'effet sur le fonctionnement d'une diode laser de l'onde émise puis réfléchie (ou rétrodiffusée) par un obstacle extérieur et revenant dans la cavité, puis le principe de son utilisation aux mesures de position et de vitesse d'un obstacle.

Le dispositif est modélisé selon le schéma de la figure 2 ; soit

réel positif le coefficient de réflexion en amplitude sur l'obstacle, qui avec la face 2 forme une cavité de longueur

. On supposera

. On désigne par

la fréquence d'oscillation de la diode laser en l'absence d'obstacle.

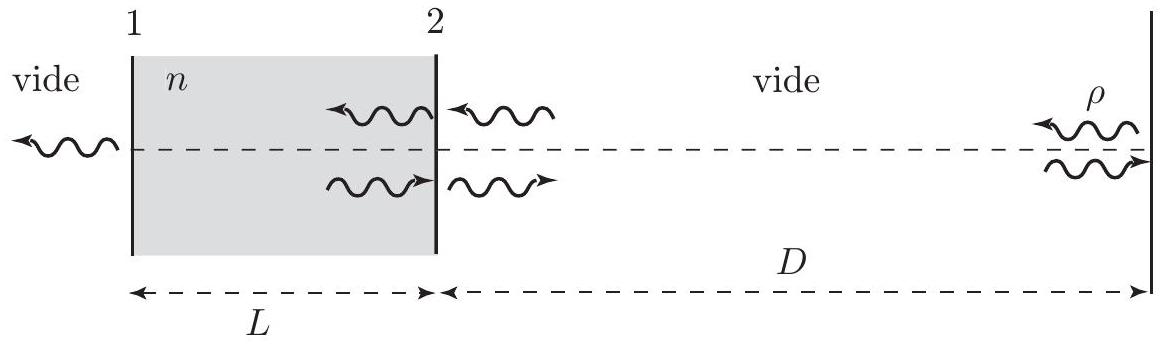
Figure 2

Justifier sans calcul que, lorsque l'onde, sortant de la face 2 , y revient en phase après un aller et retour, le coefficient d'amplification du milieu est diminué, et que la puissance du faisceau laser est alors maximale. Justifier de même que la puissance du faisceau est minimale si l'onde revient en opposition de phase.

L'indice

du milieu dépend du courant d'alimentation de la diode; en faisant varier ce courant, on modifie la fréquence de fonctionnement

; on supposera dans toute cette partie II. que cette fréquence est imposée par le contrôle du courant d'alimentation.
2. Par une rampe de courant, on réalise une croissance monotone de

; l'obstacle est fixe. On observe que la puissance émise passe par une succession de maximums.
a) Quelle est la différence de fréquence

entre deux maximums consécutifs?
b) Déterminer la relation entre le nombre

de maximums détectés,

et la distance

.
c) Pour

, exprimer

en fonction de

; quelle incertitude sur la mesure de

a-t-on par ce comptage?
3. On suppose maintenant la fréquence

fixe et l'obstacle mobile avec la vitesse

telle que

. Durant l'intervalle de temps

, on détecte

maximums de puissance laser. En utilisant les résultats précédents (2.a)), déterminer la relation entre

en supposant la vitesse constante durant

. Pour

, quelle est la résolution de la détermination de la vitesse à partir de

?
4. L'obstacle étant animé de la vitesse

, on impose au courant de commande de la diode une loi de variation « triangulaire » de durée totale

; la variation de la fréquence laser suit la
même loi : croissance de

durant

, puis décroissance jusqu'à la valeur de départ

durant

. On observe

maximums durant la première phase et

durant la seconde. Dans cette question, on suppose la vitesse

suffisamment grande et positive; d'autre part, pour simplifier, on traitera

comme des variables continues.

Déduire la distance et la vitesse de l'obstacle en fonction de

et la longueur d'onde

du rayonnement.

III - Diode laser avec cavité extérieure

Dans cette partie, on analyse quantitativement l'effet de l'onde réfléchie par l'obstacle (cf. partie II) sur l'intensité émise par la diode.

Soient et les coefficients de réflexion et de transmission pour les amplitudes dans le sens vide milieu; calculer et en fonction de ; montrer que et que .
2.a) En appliquant les relations de continuité aux ondes arrivant sur la face 2 ou en repartant (cf. figure 2), montrer que l'on peut assimiler l'ensemble à une cavité laser, de longueur identique à l'initiale, mais avec un coefficient de réflexion sur la face 2 donné, avec , par :

b) Simplifier l'expression de

en ne gardant que les termes du premier ordre en

Dans la suite, on posera

avec

.
3.a) Donner dans cette situation la nouvelle expression de la «condition laser ».
b) En déduire le coefficient d'amplification

qui maintient l'oscillation en fonction de

.
c) Soit

l'excursion maximale de

lorsque le déphasage de l'onde retour varie; exprimer

en fonction de

étant la valeur de

pour

(cf. I.4.b)). En donner la valeur numérique pour

.
4.a) Montrer que l'intensité du faisceau laser émis varie en fonction du déphasage de l'onde à son retour. Pour quelles valeurs de

est-elle maximale ? Quelle est alors la fréquence d'émission?
b) Calculer, avec les données numériques précédentes, la variation relative de l'intensité du faisceau laser

étant l'intensité moyenne.

IV - Analyse de la forme du signal

L'expérience montre que, lors du déplacement de l'obstacle ou lors d'un balayage de fréquence par modification du courant de commande (cf. partie II), on observe bien des variations presque périodiques de la puissance émise mais souvent avec des discontinuités associées à des sauts de fréquence. C'est cet effet qui est analysé dans cette dernière partie.

À partir de la « condition laser » obtenue en III.3.a), montrer, pour , que la fréquence d'oscillation est déterminée par la relation approchée :

Pour un courant de commande fixé et en l'absence d'obstacle ( ), on note et les valeurs de l'indice et du coefficient du milieu, et le module du vecteur d'onde.

En présence de l'obstacle, à la modification

est associée en fait une modification

de l'indice, avec

, où

est un coefficient positif de l'ordre de quelques unités ; cela entraîne une modification de

.
a) En linéarisant le résultat obtenu en III.3., montrer que :

.
b) Montrer de même que la «condition laser» s'écrit :

.
c) Justifier l'hypothèse

, et exprimer

en fonction de

.
3. Montrer que la relation déterminant

se met sous la forme :

avec

, et donner les expressions de

en fonction de

. Calculer

avec

. Évaluer

pour

.
4. En vue d'effectuer une analyse graphique de cette équation, préciser la valeur

qui annule

et tracer le graphe de

au voisinage de

. Porter sur ce graphe les points

correspondant aux maximums d'intensité du laser et les points

correspondant aux minimums.
5.a) À courant de commande fixé, donc

fixé, on augmente

. En traçant localement le graphe de

au voisinage de

et en suivant son déplacement (on notera que

), montrer graphiquement que, pour

augmente de façon continue mais irrégulière, et, pour

, par parties continues séparées par des sauts.
b) Lorsqu'ils existent, ces sauts de

sont accompagnés de sauts d'amplitude du faisceau laser ; quel est le sens de cette variation?
c) Dans les mêmes conditions, on diminue

; quel est alors le sens de variation des sauts d'intensité?
6. À

fixé, on augmente de façon régulière le courant de commande de la diode, ce qui augmente de même

; quel est le sens de variation de

? Quel est celui des discontinuités d'intensité dans les conditions où elles apparaissent?
7. Quel est l'intérêt de ces sauts d'intensité pour la détection?