L'objet de ce problème est l'analyse de divers mécanismes physico-chimiques susceptibles d'expliquer la montée de la sève brute dans les arbres. La sève brute est le grand courant ascendant qui conduit aux feuilles, bourgeons et fleurs, l'eau et les sels minéraux. Dans une première partie, on étudie différentes causes possibles de l'ascension de la sève : pression hydrostatique, capillarité, osmose... Cependant, une évaluation des ordres de grandeur montre qu'aucun de ces mécanismes ne peut rendre compte d'une ascension très élevée, comme dans le cas du pin Douglas où elle atteint 60 mètres. Le mécanisme principal est en fait la transpiration dont la description et le lien avec la thermodynamique de l'eau liquide font l'objet de la seconde partie.

Toutes les sous-parties sont très largement indépendantes les unes des autres. Dans tout le problème, on admettra que la sève brute est une solution si diluée que ses propriétés physiques (masse volumique, tension superficielle, équation d'état...) sont celles de l'eau pure. Sauf cas contraire, la température

sera prise à égale

Données numériques

Accélération de la pesanteur
Constante des gaz parfaits
Pression atmosphérique normale	1, 01325 bar
Masse volumique de l'eau à
Tension superficielle de l'eau à
Viscosité dynamique de l'eau à
Rayon des canaux de xylène (bois)	(conifères) à (chêne)
Température de fusion de la glace sous pression normale

Propriétés de l'eau au point critique

Masse volumique	Pression	Température

Paramètres de l'équation d'état de Speedy à


17,8297	-208 MPa

Masses molaires

Élément	C	Cl	H	O	K	Na	S
Masse molaire en g	12	35,5	1	16	39,1	23	32,1

Formulaire

A température constante, pour un corps pur de potentiel chimique , de volume molaire et à la pression , on a :

Potentiel chimique d'une mole de composant dans un mélange idéal à la température et à la pression :

où

est le potentiel chimique du composant

pur et

sa fraction molaire dans le mélange.

Loi de Poiseuille :

Première partie L'impossible montée

A. La poussée atmosphérique.

En supposant que l'eau est incompressible, quelle est la pression au sommet d'une colonne d'eau de hauteur et dont la base est à la pression atmosphérique ?
Application numérique : Quelle hauteur maximale peut atteindre l'eau soumise à une aspiration sous vide?

B. La capillarité.

A l'interface entre une phase liquide et une phase gazeuse, un accroissement réversible

de la surface de contact, à température constante, nécessite un apport énergétique par travail donné par

où

est la constante de tension superficielle entre les deux phases. Les forces de tension superficielle tendent donc à réduire la surface de contact et elles créent du côté concave une surpression par rapport au côté convexe, donnée, pour un interface sphérique de rayon

, par

On considère une goutte de liquide, sphérique, de rayon , à l'équilibre avec l'air environnant de pression uniforme ; soit la pression au sein de la goutte.
a) Donner l'expression de en fonction de et .
b) Application numérique : A partir de quel rayon la pression au sein d'une goutte d'eau est-elle supérieure de à la pression atmosphérique?
Lorsque l'on plonge un tube de verre très propre, cylindrique et de faible rayon , dans un liquide, on constate que le liquide s'élève dans le tube d'une hauteur . Le ménisque a la forme d'une calotte sphérique qui se raccorde aux parois avec un angle (voir figure 1).
a) En calculant la pression du liquide sous le ménisque de deux façons différentes, relier à et à la grandeur , dont on donnera la dimension et que l'on interprétera.
b) Que se passe-t-il si ?
c) Application numérique : Calculer pour l'eau. De quelle hauteur la sève brute peut-elle s'élever par capillarité dans les canaux de xylène qui la transportent?

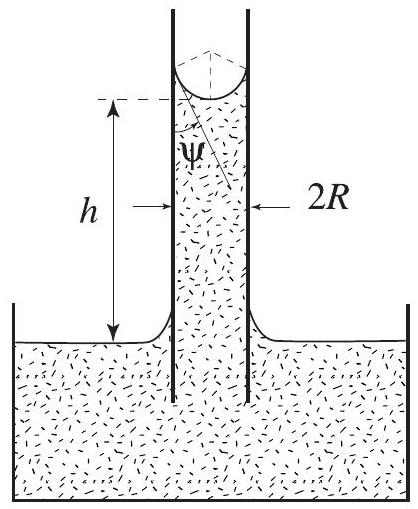
Figure 1

C. L'osmose.

On considère un récipient, formé de deux compartiments, de même volume et à la même température , séparés par une membrane semi-perméable, perméable au solvant mais non aux solutés . Le compartiment de gauche contient une solution supposée idéale, celui de droite le solvant pur (voir figure 2). On note le potentiel chimique d'une mole de pur.
a) Quelle condition est satisfaite lorsque ce système est à l'équilibre ? En déduire que les deux compartiments ne peuvent être alors à la même pression.
b) En supposant que la solution est très diluée et que le solvant est incompressible, montrer que la surpression qui s'exerce dans le compartiment , appelée pression osmotique, est de la forme : où est le nombre de moles du soluté .
c) Commenter cette loi. Où intervient la nature du ou des solutés? En quoi cette loi est-elle remarquable?
La sève brute contient en général moins d'un gramme par litre de minéraux divers (ions , ) et parfois des substances organiques.
a) Estimer la pression osmotique de la sève brute par rapport à l'eau pure en ne tenant compte que des sels minéraux.
b) Certains arbres, comme l'érable, ont au début du printemps, une sève riche en sucres : la concentration

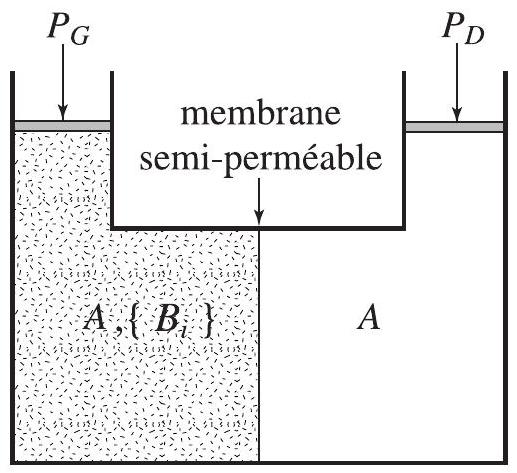
Figure 2

de disaccharides (formule brute :

) peut alors atteindre 20 à 30 grammes par litre. Quelle est alors la pression osmotique de la sève brute par rapport à l'eau pure?
c) Expérimentalement, on constate qu'à la base des végétaux, la sève brute est bien émise sous pression : on trouve des pressions de l'ordre de 1 bar et plus, en excès par rapport à la pression atmosphérique. Est-il raisonnable de considérer cette poussée radiculaire comme étant pour une large part de nature osmotique?
d) Application numérique : De quelle hauteur

la sève brute peut-elle s'élever sous l'effet de la poussée radiculaire?

D. La perte de charge.

L'eau est un fluide visqueux et son écoulement s'accompagne nécessairement d'une perte de pression. Pour un écoulement stationnaire dans un conduit cylindrique vertical, de longueur

et de section circulaire de rayon

, la perte de charge

qui se produit en sus de la variation hydrostatique étudiée à la question I.A.1, est relié au débit volumique

par la loi de Poiseuille.

Les canaux de xylène, approximativement cylindriques, présentent une dispersion en taille. Quels sont ceux qui transportent principalement la sève brute?
Des mesures donnent des vitesses moyennes d'ascension de l'ordre de pour les conifères et jusqu'à pour des arbres à gros canaux comme le chêne.
a) En déduire la perte de charge théorique par unité de longueur pour ces deux types d'arbres. Que constate-t-on?
b) Les mesures expérimentales sont dans un facteur d'environ 2 par rapport aux prévisions
théoriques. Dans quel sens ce facteur joue-t-il? Justifier.
c) La perte de charge est-elle significative par rapport à la poussée radiculaire ?
E. Quels sont, parmi les mécanismes précités, ceux qui vous semblent les plus à même d'expliquer la montée de la sève? Montrer que la montée de la sève dans les très grands conifères demeure inexplicable à ce stade.

Deuxième partie La transpiration

En fait, l'essentiel de la sève s'évapore dans l'atmosphère au niveau des feuilles. Par ailleurs, on sait par traçage radioactif qu'il y a continuité de la colonne d'eau depuis les racines jusqu'aux feuilles.
A. Un analogue saisissant de ce mode de transport de la sève est donné par l'expérience de J. Böhm (1893). Un récipient, en argile poreuse, est plongé dans un bain d'eau bouillante. L'eau du récipient est siphonnée, par l'intermédiaire d'un tube capillaire, au travers d'une bouteille contenant du mercure. Lorsque l'on retire le bain bouillant, on constate que l'eau reflue dans le tube en tirant à elle une colonne de mercure qui peut atteindre 1 m de hauteur (voir figure 3 ).

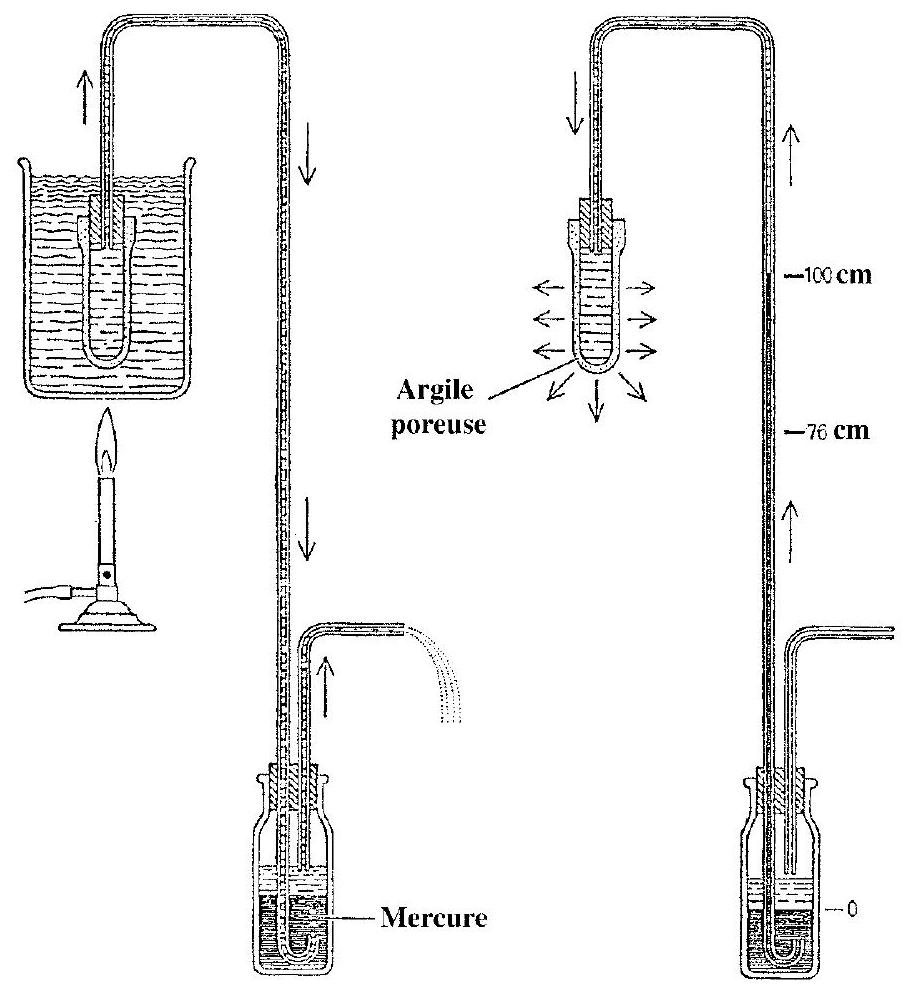
Figure 3

Quelle est la pression dans le tube au niveau de l'interface eau/mercure? En quoi est-ce remarquable?
Expliquer en quelques lignes en quoi cette expérience éclaire le mécanisme de la montée de la sève par transpiration.
L'argile poreuse est un entrelacs de pores de tailles et de formes variées dans lequels existent des ménisques entre l'air et l'eau liquide. Quelle doit-être la largeur approximative de ces pores pour provoquer une telle dépression? (on se référera à I.B).
Qu'adviendrait-il si jamais une bulle apparaissait dans l'eau?
B. L'expérience de Böhm montre que l'eau liquide peut être stable sous traction. Dans tout ce qui suit, on cherche à évaluer quelle tension (force de traction par unité de surface) l'eau liquide peut supporter sans se rompre.

Un cylindre de section

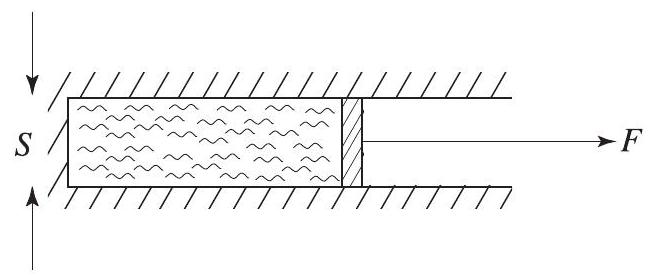
, parfaitement étanche et fermé par un piston sur lequel on tire avec une force

(figure 4a), contient un liquide maintenu à température constante. À partir d'une certaine force, le liquide se rompt.

Figure

On admet que la colonne de liquide se rompt en deux, tout en conservant son volume, et que la surface de séparation créée est plane et bien nette (voir figure 4b). Exprimer à l'aide de la tension superficielle du liquide le travail qu'il a fallu fournir pour créer cette séparation.
est l'opposé du travail des forces attractives à très courte portée (moins de 10 nm ) qui s'exercent entre les molécules de part et d'autre de la surface de séparation. Quelle est l'origine microscopique de ces forces attractives?
Application numérique : En supposant que soit fourni par une force constante sur la distance adéquate , calculer pour l'eau à puis la tension correspondante , que l'on exprimera en bar. On prendra .
Que vaut la pression de l'eau juste avant la rupture? Ce résultat est-il compatible avec l'expérience de Böhm?
C. On considère un fluide de volume molaire , à la pression et à la température , dont l'équation d'état est, dans un domaine de température et de pression, correctement décrite par
l'équation de Van der Waals :

où

sont des constantes. On appelle compressibilité isotherme

la quantité :

Calculer pour le fluide de Van der Waals.
Quel doit-être, selon vous, le signe de pour que le fluide soit mécaniquement stable?

On appelle spinodale le lieu des points, dans le diagramme (

), pour lesquels la compressibilité diverge, soit

.
3. Montrer que l'équation de la spinodale du fluide de Van der Waals en coordonnées

est donnée par :

En déduire l'équation de la spinodale en coordonnées .
Tracer l'allure de la spinodale dans le diagramme ( ) en indiquant les zones où le fluide n'est pas stable mécaniquement.
Calculer les coordonnées du sommet de la spinodale, puis la température correspondante .
Tracer, dans le plan ( ), l'allure des isothermes du fluide de Van der Waals. Justifier physiquement pourquoi est confondu avec le point critique du fluide, point dont on rappellera la définition.
Dans les conditions expérimentales courantes, pour une température donnée inférieure à , certaines parties de l'isotherme ne sont pas observées expérimentalement; une portion est remplacée par un « palier » à constante, d'extrémités et (avec ). Quelle est la condition d'équilibre thermodynamique que doit satisfaire le fluide en et en et qui détermine la position de ce palier.
Indiquer sur le graphe de cette isotherme de Van der Waals les parties correspondant au fluide stable, instable, métastable.
D. On introduit les coordonnées réduites et .
Montrer que, pour un fluide de Van der Waals, le rapport est universel (indépendant de et ). Application numérique : Est-ce bien vérifié dans le cas de l'eau?
Donner dans le diagramme ( ) l'équation de la spinodale. A quel volume réduit la pression s'annule-t-elle sur la spinodale? Quelle est la température réduite correspondante?
Application numérique : Comparer pour l'eau ces prédictions avec les valeurs expérimentales d'annulation de la pression : et un volume massique .
Application numérique : Calculer approximativement, pour l'eau, la pression sur la spinodale côté liquide à . Comparer avec la valeur trouvée en II.B.4.
Application numérique : Calculer la pression à pour une masse volumique . A quel résultat devrait-on s'attendre? Que constate-t-on?
E. Ainsi, à la température ambiante, l'équation d'état de van der Waals ne décrit plus correctement l'eau liquide. Speedy a proposé en 1982 l'équation d'état suivante :

où

sont des fonctions de la température, obtenues en ajustant au mieux les mesures d'équation d'état de l'eau liquide sur le domaine

Application numérique : Calculer pour une pression de 1 atm à la masse volumique de l'eau. Que pensez-vous de la qualité de l'ajustement?
Calculer pour l'équation d'état de Speedy. Comment interpréter et ?
Montrer que l'équation d'état de Speedy s'obtient, à température fixée, en faisant un développement limité de la pression en fonction de autour de , tronqué au second ordre. En déduire une expression de .
La valeur de la pression de l'eau liquide à la limite de la métastabilité prédite par Speedy à est proche de la valeur expérimentale. Par ailleurs, des mesures donnent une pression de la sève de l'ordre de -1 MPa au sommet des végétaux. Qu'en concluez-vous?