Version interactive avec LaTeX compilé
PREMIÈRE COMPOSITION DE PHYSIQUE
L'utilisation des calculatrices est autorisée pour cette épreuve.
Mesure de l'activité sismique d'une étoile par interférométrie
Le dispositif étudié constitue un interféromètre compact dédié à l'étude sismique de sources stellaires. Le principe proposé, un peu moins efficace qu'un spectromètre à réseau, conduit à un instrument bien moins encombrant et bien moins coûteux. Le principe de l'interféromètre est analysé, ainsi que son installation au foyer d'un télescope et son fonctionnement dans des conditions d'observation réalistes.
On suppose, dans tout le problème, les optiques idéales : lentilles parfaitement transparentes, miroirs totalement réfléchissants, lames semi-réfléchissantes divisant le faisceau incident en deux faisceaux d'intensités lumineuses égales.
Un soin tout particulier devra être apporté aux applications numériques.
Grandeurs physiques
| Vitesse de la lumière : |
|
| Constante de Boltzmann : |
|
| Constante des gaz parfaits : |
|
| Masse de l'atome d'hydrogène : |
|
| Masse molaire de l'hydrogène atomique : |
|
I - Interférométrie
Dans tout ce qui suivra on notera
- La figure 1 correspond au montage de principe d'un interféromètre de Michelson. Les miroirs sont réglés de telle façon que l'on observe des anneaux d'interférence circulaires sur l'écran
placé dans le plan focal de la lentille , de distance focale image .
a) Quel est le rôle de la lame semi-réfléchissante? Quel est celui de la lentille ?
b) Montrer qu'avec ce montage la moitié du flux incident est irrémédiablement perdue.

Figure 1
- La différence de marche, différence entre les deux chemins optiques pour un rayon entrant perpendiculairement au miroir (1), est notée
; pour un rayon entrant avec une inclinaison , on rappelle que la différence de marche est alors donnée par .
a) L'interféromètre est éclairé par une source étendue, supposée strictement monochromatique de nombre d'onde. On suppose la tache centrale en brillante. Exprimer le rayon du anneau sombre, en fonction de et . Faire un schéma de ce que l'on observe sur l'écran.
b) La source est l'image d'une étoile, telle celle fournie par un télescope. Cette image est étalée par la diffraction mais surtout par la turbulence atmosphérique, ce qui donne des rayons entrant dans l'interféromètre d'inclinaisons diverses mais faibles. Quelle est la figure d'interférence observée en fonction deen présence d'un filtre interférentiel qui sélectionne une très étroite bande passante autour d'un nombre d'onde donné. - On éclaire l'interféromètre par une source monochromatique, de nombre d'onde
. Un détecteur est placé au foyer de la lentille . Ce détecteur délivre un signal , proportionnel à l'intensité lumineuse au point . Ce signal sera appelé dans la suite interférogramme. Il dépend de la différence de marche .
a) Montrer queest donné par : . Que représente ?
b) Quelle est la période de l'interférogramme? - On illumine l'interféromètre par une source présentant un doublet de nombres d'onde
et voisins. Chacune des raies est supposée monochromatique et leurs intensités sont égales.
a) Déterminer l'expression de l'interférogrammecorrespondant. Mettre en évidence deux périodes caractéristiques dans .
b) Application numérique : Représenter l'allure de l'interférogramme pour le doublet du sodium :et .
II - Interférogramme d'une raie élargie
- On suppose maintenant que le profil spectral de la source n'est plus monochromatique mais possède une largeur
. On désigne par l'intensité spectrale : dans l'intervalle l'intensité émise est . On admettra que les rayonnements correspondant à chaque intervalle de largeur sont incohérents. On notera l'intensité lumineuse totale de la raie. est donc donnée par la somme des intensités de chaque intervalle :
Dans la suite, on prend
a) Montrer alors que le signal détecté est donné par :
b) Quelle est la plus petite valeur
2. On illumine l'interféromètre avec une source stellaire via un filtre de bande passante
a) Montrer que, d'après la question précédente, on peut négliger dans le signal interférométrique tout terme interférentiel associé au spectre large délimité par le filtre si
b) Quelle est la plus petite valeur
2. On illumine l'interféromètre avec une source stellaire via un filtre de bande passante
a) Montrer que, d'après la question précédente, on peut négliger dans le signal interférométrique tout terme interférentiel associé au spectre large délimité par le filtre si

Figure 2
b) En déduire que l'interférogramme s'écrit :
où
III - Élargissement et décalage possibles des raies spectrales. Évaluation de la différence de marche optimale
Une cause possible d'élargissement ou de décalage (en nombre d'onde) d'une raie spectrale est associée au mouvement relatif de la source et de l'observateur (effet Doppler). Soit
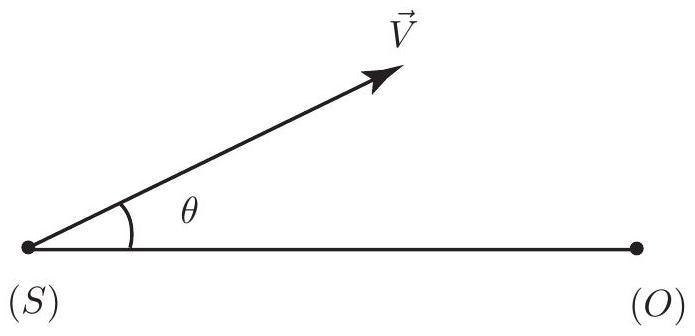
Figure 3
où
- À la surface d'une étoile, les atomes (majoritairement de l'hydrogène) sont supposés former un gaz parfait à l'équilibre thermodynamique de température
.
a) Quelle est la vitesse quadratique moyenned'un atome de cette étoile?
b) La dispersion des vitesses entraîne par conséquent un élargissementde la raie symétrique autour de la valeur . Donner l'ordre de grandeur de en fonction de et .
c) Application numérique : Évaluerpour et . - La rotation de l'étoile est aussi un paramètre dont il faut tenir compte. On note
l'angle entre la direction de visée et l'axe de rotation stellaire.
a) Pour quelle valeur del'influence de la rotation sur la largeur de raie sera-t-elle nulle? maximale? Dans ce dernier cas, expliquer qualitativement pourquoi la rotation de l'étoile, phénomène parfaitement déterminé, conduit à un élargissement de la raie d'émission analogue à celui associé aux mouvements erratiques des atomes et analysé dans la question précédente.
b) Toujours dans le cas d'une influence maximale de la rotation, évaluer la contribution de la rotation stellaireà la largeur de raie en fonction de la vitesse équatoriale de rotation de la surface de l'étoile. Pour quelle vitesse équatoriale de rotation ce dernier terme est-il comparable à ?
c) Application numérique : dans ce dernier cas, calculerpour une étoile dont la température de surface est . - On désire utiliser l'interféromètre comme sismomètre pour détecter les mouvements oscil-
latoires de la surface stellaire. Une oscillation sismique est assimilée à une variationde la vitesse apparente vers l'observateur de l'ensemble de la couche externe de l'étoile. On suppose cette variation sinusoïdale, d'amplitude , de pulsation . Le spectre d'émission et d'absorption de l'étoile est celui de la question II.2. Cette utilisation ne requiert que l'enregistrement de l'interférogramme pour une valeur optimisée de la différence de marche notée . En l'absence de signal sismique, l'interférogramme est de II.2.b).
a) Montrer qu'à l'instant, l'interférogramme peut être mis sous la forme :
où
b) Montrer que cette relation implique, pour une détection optimale, le choix d'une différence de marche
c) Montrer alors que le principe instrumental conduit à mesurer un déphasage
4. Au décalage Doppler sismique du spectre stellaire, enregistré sur une nuit entière, se superposent diverses contributions. Estimer succinctement l'influence du mouvement de rotation de la Terre pour une observation menée dans un observatoire situé à la latitude
c) Montrer alors que le principe instrumental conduit à mesurer un déphasage
4. Au décalage Doppler sismique du spectre stellaire, enregistré sur une nuit entière, se superposent diverses contributions. Estimer succinctement l'influence du mouvement de rotation de la Terre pour une observation menée dans un observatoire situé à la latitude
IV - Amélioration du montage interférométrique
- Un montage plus efficace que le montage de principe de type Michelson est proposé sur la figure 4. Il reçoit un faisceau de lumière parallèle monochromatique. Il permet de récupérer le flux total incident en utilisant deux détecteurs placés aux deux sorties possibles des faisceaux qui interfèrent.
a) On suppose que le premier détecteur délivre un interférogramme :
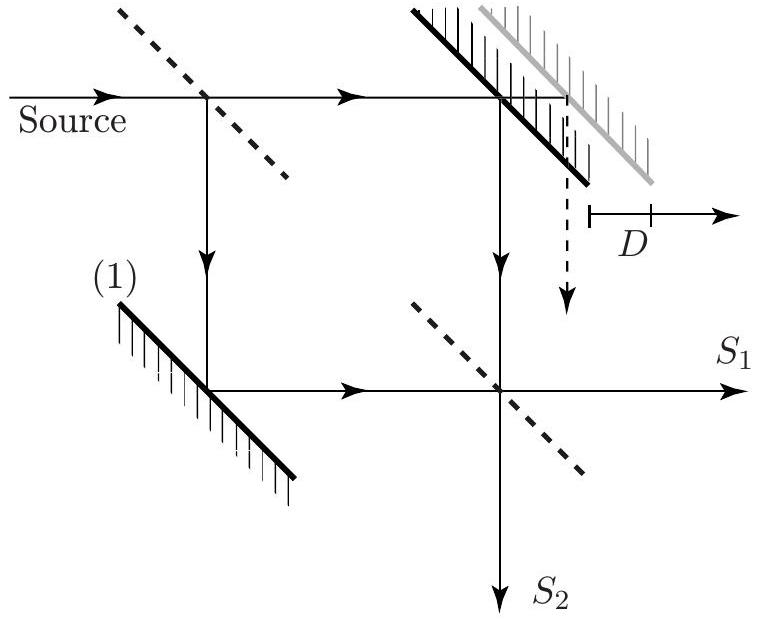
Figure 4
En admettant que les pertes d'énergie lumineuse dans l'appareil sont négligeables, déduire la forme de l'interférogramme
b) Montrer comment une combinaison de
c) Montrer que la recombinaison géométrique des faisceaux sur la deuxième lame semiréfléchissante suppose la symétrie du montage, et donc une observation à différence de marche nulle. Cela est-il intéressant pour l'observation sismique stellaire discutée plus haut?
2. On interpose, contre l'un des miroirs, une lame de verre à faces parallèles, d'épaisseur uniforme
a) Montrer que, pour une incidence
b) Montrer comment une combinaison de
c) Montrer que la recombinaison géométrique des faisceaux sur la deuxième lame semiréfléchissante suppose la symétrie du montage, et donc une observation à différence de marche nulle. Cela est-il intéressant pour l'observation sismique stellaire discutée plus haut?
2. On interpose, contre l'un des miroirs, une lame de verre à faces parallèles, d'épaisseur uniforme
a) Montrer que, pour une incidence
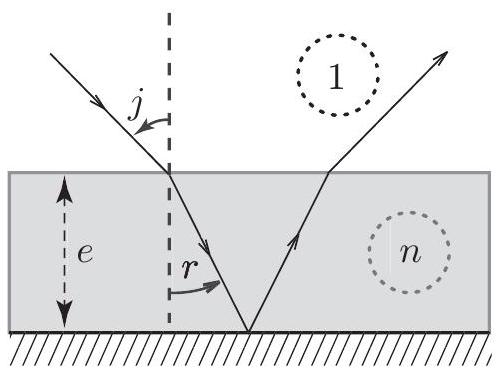
Figure 5
b) Application numérique : On cherche à imposer une différence de marche de
c) Par un schéma, montrer que ce montage optique permet alors la recombinaison exacte des faisceaux sur la
c) Par un schéma, montrer que ce montage optique permet alors la recombinaison exacte des faisceaux sur la
V - Effet de la turbulence atmosphérique
- L'interféromètre reçoit le flux d'une étoile, objet à l'infini, collecté par un télescope. On suppose le système optique du collecteur équivalent au montage de la figure 6. Ce montage est dit afocal : le foyer image de
est confondu avec le foyer objet de . La lentille représente le miroir primaire du télescope, de diamètre . La lentille alimente l'interféromètre: le flux issu de est divisé par la première lame semiréfléchissante de la figure 4.
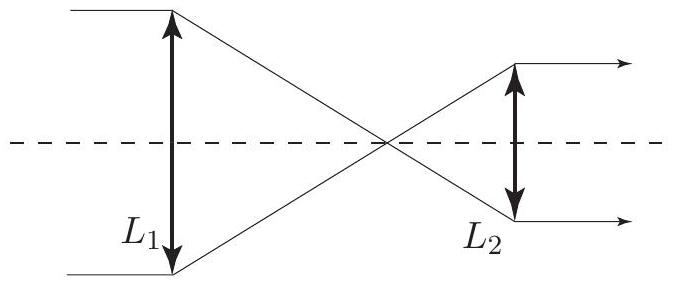
Figure 6
a) Justifier l'intérêt de ce montage afocal pour alimenter l'interféromètre.
b) Exprimer le grandissement angulaire
c) Déterminer la taille
a du collecteur. En déduire le diamètre minimal des pièces optiques de l'interféromètre. Le calculer pour
2. La tache image de l'étoile n'est en fait ni limitée par la seule diffraction du collecteur, ni stable. La turbulence de l'atmosphère terrestre dévie et étale le faisceau stellaire incident. On s'intéresse principalement à la déviation atmosphérique du faisceau incident, notée
a) Déterminer l'angle
b) Estimer la différence de marche
c) Exprimer la condition sur l'inclinaison maximale admissible dans l'instrument, pour que les fluctuations en différence de marche restent inférieures à une fraction
d) Application numérique : On fixe
3.a) Montrer que la turbulence conduit à une mesure de vitesse parasite
b) Exprimer le grandissement angulaire
c) Déterminer la taille
a du collecteur. En déduire le diamètre minimal des pièces optiques de l'interféromètre. Le calculer pour
2. La tache image de l'étoile n'est en fait ni limitée par la seule diffraction du collecteur, ni stable. La turbulence de l'atmosphère terrestre dévie et étale le faisceau stellaire incident. On s'intéresse principalement à la déviation atmosphérique du faisceau incident, notée
a) Déterminer l'angle
b) Estimer la différence de marche
c) Exprimer la condition sur l'inclinaison maximale admissible dans l'instrument, pour que les fluctuations en différence de marche restent inférieures à une fraction
d) Application numérique : On fixe
3.a) Montrer que la turbulence conduit à une mesure de vitesse parasite
b) Application numérique : Calculer
