Version interactive avec LaTeX compilé

X ENS Option Informatique MP 2011

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

X-ENS MP X-ENS 2011 MP Info Info 2011

2025_08_29_59c83a621577e6e0eaafg

ÉCOLE POLYTECHNIQUE - ÉCOLES NORMALES SUPÉRIEURES

COMPOSITION D'INFORMATIQUE - A - (XULC)
(Durée : 4 heures)

L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
Le langage de programmation choisi par le candidat doit être spécifié en tête de la copie.

Transmission dans les arbres

On étudie dans ce problème des algorithmes de transmission d'informations dans les arbres, avec le modèle dit "du téléphone". Dans la partie I, on étudie les arbres binomiaux. Dans la partie II, on considère plusieurs calculs élémentaires sur les arbres. Dans la partie III, on étudie la diffusion de l'information à partir de la racine de l'arbre. Dans la partie IV, on s'intéresse à l'échange total d'informations entre tous les nœuds d'un arbre. Les parties I et II sont indépendantes.

Algorithmes et programmes

Pour les questions qui demandent la conception d'un algorithme : il s'agit de donner une description concise mais précise, en français, d'un algorithme effectuant la tâche indiquée.
Pour les questions qui demandent l'écriture d'un programme : il s'agit d'exprimer votre algorithme dans un langage de programmation de votre choix. La lisibilité de votre programme (notamment : mise en évidence de sa structure, indentation, commentaires pertinents) sera prise en compte dans l'évaluation.
Lorsqu'elle est demandée, la complexité d'un algorithme ou d'un programme ne sera pas calculée exactement mais seulement estimée en ordre de grandeur, avec des expressions du type , etc., où sont des paramètres en entrée de l'algorithme.
Lorsqu'une question demande d'écrire un programme, et qu'une certaine complexité est exigée, on ne demande pas de faire la preuve que le programme proposé a effectivement cette complexité.

Définitions

Un arbre est défini par la donnée d'un entier , appelé nœud, et d'une liste d'arbres , éventuellement vide. Si la liste est vide, on dit que est un nœud externe. Sinon, la liste comprend éléments , on dit que est un nœud interne, que les nœuds sont les fils de , et que est le père des .
Tous les nœuds de sont supposés distincts. On note l'ensemble de tous les nœuds de et leur nombre.
Dans un arbre, les voisins d'un nœud sont son père (s'il existe) et ses fils.
Entre deux nœuds et de il existe un unique chemin, composé de nœuds deux à deux distincts, tels que , et et sont voisins pour . On note chemin ce chemin et on dit que est sa longueur.
Le nœud est appelé la racine de .
La profondeur d'un nœud est la longueur de chemin ; en particulier, la racine a pour profondeur 0 . La profondeur de est le maximum de la profondeur de ses nœuds.

Les arbres seront représentés en Caml et en Pascal de la manière suivante :

    (* Caml *) { Pascal }
type arbre = type arbre = `noeud;
| Noeud of int * arbre list;; liste_arbre = ^element;
        noeud = record n :integer; l :liste_arbre; end;
        element = record a :arbre; r :liste_arbre; end;

Certaines questions font par ailleurs intervenir des listes d'entiers, qui seront représentées par le type liste suivant :

type liste == int list ; ; | type liste = ^entier ;
    entier = record e :integer; s :liste; end;

Partie I. Arbres binomiaux

Dans cette partie, on étudie des arbres particuliers, appelés "binomiaux".
Soit

un entier positif ou nul. Un arbre binomial d'ordre

est défini comme suit :

un arbre binomial d'ordre 0 est réduit à sa racine;
si , un arbre binomial d'ordre est de la forme où chaque est un arbre binomial d'ordre .

Dans la suite,

désigne un arbre binomial d'ordre

Question 1 Dessiner

, avec une numérotation des nœuds de votre choix.

Question 2 Quel est le nombre de nœuds de

? Combien sont externes?

Question 3 Pour

, montrer qu'on peut aussi définir récursivement

à l'aide de deux copies de

Question 4 Écrire une fonction copie qui prend en arguments un entier

et un arbre

et renvoie une copie de l'arbre

dans laquelle chaque nœud de numéro

est remplacé par un nœud de numéro

(* Caml *) copie : int -> arbre -> arbre
{ Pascal } function copie(n : integer; t : arbre) : arbre;

Question 5 Écrire une fonction bin qui prend en argument un entier

et qui renvoie l'arbre

, avec une numérotation des nœuds de votre choix. On garantira une complexité proportionnelle au nombre de nœuds de

(* Caml *) bin : int -> arbre
{ Pascal } function bin(k : integer) : arbre;

Question 6 Quelle est la profondeur de

? Quelle est la longueur maximale d'un chemin entre deux nœuds?

Question 7 Combien de nœuds ont une profondeur donnée

Question 8 Pour

, on définit

comme un arbre de racine

et à

nœuds, qu'on obtient avec la numérotation suivante des nœuds : la racine

a le numéro 1, et le père du nœud de numéro

, où

, est le nœud de numéro

, où la notation

désigne le plus petit entier supérieur ou égal à

. Dessiner

. Justifier que la définition de

conduit bien à un arbre. Donner, sans la justifier, une relation entre

Question 9 Écrire une fonction cn qui prend en argument un entier

et qui renvoie l'arbre

. On garantira une complexité

(* Caml *) cn : int -> arbre
{ Pascal } function cn(n : integer) : arbre;

Partie II. Fonctions élémentaires sur les arbres

Question 10 Écrire une fonction profondeur qui prend en argument un arbre

et renvoie sa profondeur. On garantira une complexité

(* Caml *) profondeur : arbre -> int
{ Pascal } function profondeur(t : arbre) : integer;

Question 11 Écrire une fonction noeud_externe_max qui prend en argument un arbre

et qui renvoie le numéro d'un nœud externe de

de profondeur maximale. En cas d'égalité, on choisira arbitrairement. On garantira une complexité

(* Caml *) noeud_externe_max : arbre -> int
{ Pascal } function noeud_externe_max(t : arbre) : integer;

Question 12 Soit

un arbre de racine

un nœud de

. Écrire une fonction chemin qui prend en arguments

et renvoie l'unique chemin de

sous la forme d'une liste d'entiers

avec

père de

pour

. On garantira une complexité

(* Caml *) chemin : arbre -> int -> liste
{ Pascal } function chemin(t : arbre; s : integer) : liste;

Question 13 Soit

un arbre et

un nœud de

. On définit l'arbre obtenu par changement de racine

, noté

, comme l'arbre

de racine

dont les noeuds sont les mêmes que ceux de

et tel que deux nœuds sont voisins dans

si et seulement s'ils le sont dans

Écrire une fonction pivot qui prend en arguments

et renvoie l'arbre pivot

. On garantira une complexité

. S'il y a plusieurs tels arbres

, on en choisit un arbitrairement.

(* Caml *) pivot : arbre -> int -> arbre
{ Pascal } function pivot(t : arbre; s : integer) : arbre;

Question 14 Étant donné un arbre

, on définit son diamètre comme la longueur du plus long chemin dans

. Soit

l'un des nœuds externes de

de profondeur maximale, et

l'arbre obtenu à partir de

par changement de racine

. Montrer que le diamètre de

est égal à la profondeur de

Question 15 En déduire une fonction diametre qui prend en argument un arbre et qui renvoie son diamètre.

(* Caml *) diametre : arbre -> int
{ Pascal } function diametre(t : arbre) : integer;

Question 16 Soit

un arbre de diamètre

. Montrer que

est la plus grande profondeur d'un arbre obtenu par changement arbitraire de racine et que

est la plus petite profondeur d'un arbre obtenu par changement arbitraire de racine.

Partie III. Diffusion dans les arbres

On étudie dans cette partie le problème de la diffusion dans les arbres. La racine

de l'arbre

possède un message qu'elle doit transmettre à tous les autres nœuds. La diffusion procède par étapes, toutes de temps unitaire. À une étape donnée, chacun des nœuds déjà en possession du message le transmet à un et un seul de ses fils (sauf si tous ses fils l'ont déjà reçu). Une diffusion

est caractérisée par un ensemble de fonctions : à chaque nœud interne

de l'arbre, avec

fils, on associe une fonction injective

qui numérote ses fils de 1 à

dans l'ordre dans lequel

leur transmet le message.

Pour

, on note

le numéro de l'étape à laquelle

reçoit le message :

è

Voici un exemple :

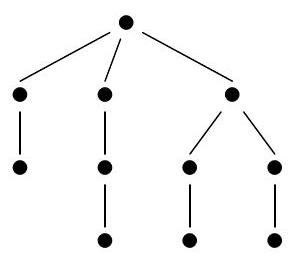
Un arbre

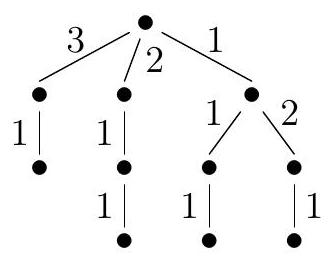
Valeurs des fonctions

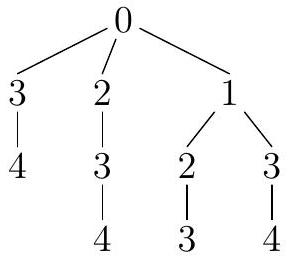
Valeurs des numéros des étapes

La durée de la diffusion est son nombre d'étapes, soit

. Une diffusion est optimale si sa durée est minimale parmi les durées de toutes les diffusions.

Diffusion dans les arbres binomiaux

On considère l'arbre binomial

défini dans la partie I. Tout noeud interne

a pour fils les racines

d'arbres binomiaux

. La numérotation naturelle s'obtient en posant

pour chaque nœud

et chaque

, tandis que la numérotation renversée s'obtient en posant

Question 17 Quelle est la durée de la diffusion qui choisit la numérotation naturelle pour chaque nœud?

Question 18 Même question pour la diffusion qui choisit la numérotation renversée pour chaque nœud.

Question 19 Quelle est la durée d'une diffusion optimale dans

? Justifier votre réponse.

Diffusion dans un arbre quelconque

Question 20 Proposer un algorithme pour déterminer une diffusion optimale dans un arbre

quelconque. Quelle est sa complexité en fonction de

Question 21 Écrire une fonction diffusion_optimale qui prend en argument un arbre

et qui calcule la durée d'une diffusion optimale pour

. (On pourra supposer que le langage de programmation contient une fonction qui trie un tableau ou une liste d'entiers.)

(* Caml *) diffusion_optimale : arbre -> int
{ Pascal } function diffusion_optimale(t : arbre) : integer;

Durée de la diffusion optimale

Question 22 Donner une borne supérieure pour la durée d'une diffusion optimale dans un arbre arbitraire à

nœuds, et exhiber pour tout

un arbre pour lequel cette borne est atteinte.

Question 23 Donner une borne inférieure pour la durée d'une diffusion optimale dans un arbre arbitraire à

nœuds, et exhiber pour tout

un arbre pour lequel cette borne est atteinte.

Partie IV. Échange total dans les arbres

On étudie dans cette partie le problème de l'échange total dans les arbres. Chaque nœud

de l'arbre possède un message

qu'il doit transmettre à tous les autres nœuds. L'échange total procède par étapes, toutes de temps unitaire. Lors d'une étape, certaines paires de voisins s'échangent tous les messages qu'ils ont reçus dans les étapes précédentes; chaque nœud ne peut communiquer qu'avec un seul voisin lors d'une étape donnée. La durée d'un échange total est son nombre d'étapes, et son trafic est le nombre d'échanges entre voisins ayant eu lieu au cours de l'algorithme. Voici un exemple pour un arbre à 4 nœuds, dont la durée est 3 et le trafic 5 :

Étape 0

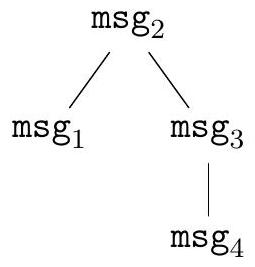
Étape 2

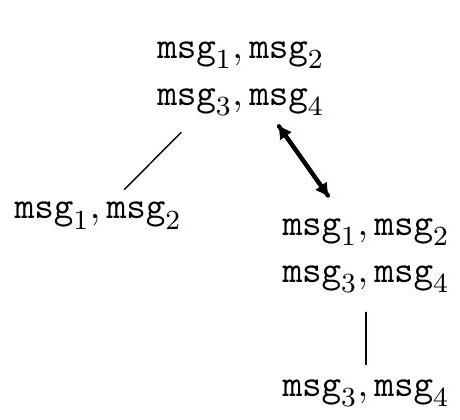
Étape 1

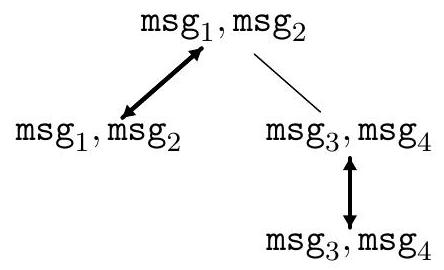
Étape 3

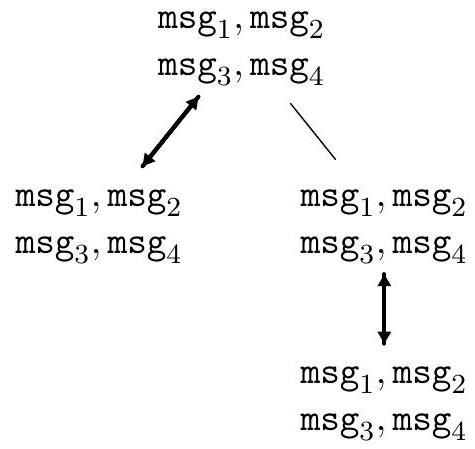
Échange total dans les arbres binomiaux

On revient dans cette question sur l'arbre binomial

d'ordre

introduit dans la partie I .

Question 24 Proposer un algorithme d'échange total dans

dont la durée est

Question 25 Montrer que tout échange total dans

a une durée au moins égale à

Question 26 Plus généralement, donner une borne inférieure pour la durée de tout échange total dans un arbre

quelconque à

nœuds.

Échange total de trafic minimal

Soit

un arbre à

nœuds. On considère l'échange total suivant, où il y a un seul échange à chaque étape :

Tant que l'arbre contient au moins trois nœuds :
(a) On choisit un nœud externe (arbitrairement s'il y en a plusieurs), qui effectue un échange avec son père;
(b) On efface le nœud de l'arbre.
Les deux derniers nœuds échangent leur information et possèdent désormais les messages de tous les nœuds de .
On effectue à nouveau tous les échanges de l'étape 1, dans l'ordre inverse, pour propager l'information à tous les nœuds.

Question 27 Montrer que le trafic de l'échange total précédent est égal à

Question 28 Écrire une fonction echange_total qui prend en argument un arbre

et renvoie la liste des

nœuds externes successivement retirés de l'arbre

par l'étape 1 de l'algorithme d'échange total ci-dessus. On garantira une complexité

(* Caml *) echange_total : arbre -> liste
{ Pascal } function echange_total(t : arbre) : liste;

Question 29 Montrer que le trafic de tout échange total dans un arbre à

nœuds est au moins égal à