Version interactive avec LaTeX compilé
ÉCOLE POLYTECHNIQUE
filières PSI et PT
ÉPREUVE D'INFORMATIQUE
(Durée : 2 heures)
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
Le langage de programmation choisi par le candidat doit être spécifié en tête de la copie.
Le langage de programmation choisi par le candidat doit être spécifié en tête de la copie.
Tournois et Pronostics
Cettc épreuve traite des tournois à ćlimination directe tels qu'on en rencontre en sport. La première partie concerne lcurs représentations. La deuxième partic consiste à exhiber les vainqueurs possibles d'un tournoi en fonction si l'on connait à l'avance les résultats de tous les matchs possibles. Enfin la troisième partie calcule les chances de victoire de chaque joueur en fonction de pronostics donnés pour chaque match possible.
La complexité, ou le temps d'exécution, d'un programme
De manière générale, on s'attachera à garantir une complexité aussi petite que possible dans les fonctions écrites. Le candidat y sera tout particulièrement sensible lorsque la complexité d'une fonction est demandée. Dans ce cas, il devra de plus justifier cette dernic̀re si elle ne se déduit pas directement de la lecture du code.
Dans tout le sujet, on considère que le nombre de joueurs est fixé à
Partie I. Tournois
Dans cette partie, on s'intéresse à la représentation et à la manipulation de tournois à ćlimination directe entre
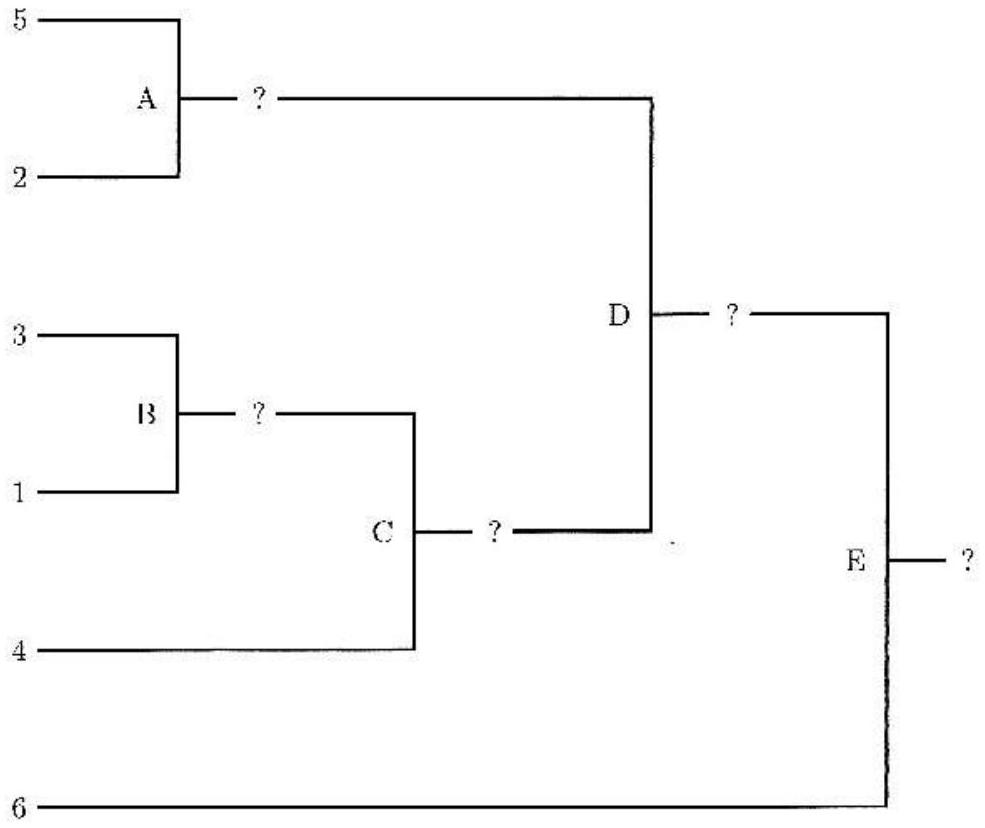
Figure 1 - Un tournoi à 6 joueurs.
Afin de représenter un tournoi en machinc, on va identifier les matchs avec les entiers
Par la suite, on identifiera pour tout entier
réels. Par excmple, le tournoi précédent pourra ctre représenté par le tableau suivant :
réels. Par excmple, le tournoi précédent pourra ctre représenté par le tableau suivant :
Bien sûr toute matrice d'entiors
(1) pour tout
(2) pour tout
(3) pour tout
(4) pour tout
(5) pour tout
(1) pour tout
(2) pour tout
(3) pour tout
(4) pour tout
(5) pour tout
Question 1 Donner une interprétation en français des conditions (3), (4) et (5) exprimées cidessus pour qu'une matrice
Question 2 Ferire une fonction EstVraiCondition5
Question 3 Écrire une fonction EstUnTournoi (T) qui prend en argument une matrice d'entiers et qui renvoie true si
On s'intéresse maintenant à la manière dont se déroule le tournoi, à l'aide de matrices, appelées oracles, qui prédiscnt le résultat de chaque match possible. Un oracle
|
|
1 | 2 | 3 | 4 | 5 | 6 |
| 1 | true | true | false | true | true | false |
| 2 | false | true | true | true | false | true |
| 3 | true | false | true | true | false | true |
| 4 | false | false | false | true | false | false |
| 5 | false | true | true | true | true | false |
| 6 | true | false | false | true | true | true |
Figure 2 Exemple d'un oracle.
Question 4 Écrirc une fonction EstUnOracle
La donnée d'un tournoi et d'un oracle détermine la manière dont se déroule le tournoi. Dans notre exemple, on obtient le résultat décrit dans la figure 3.
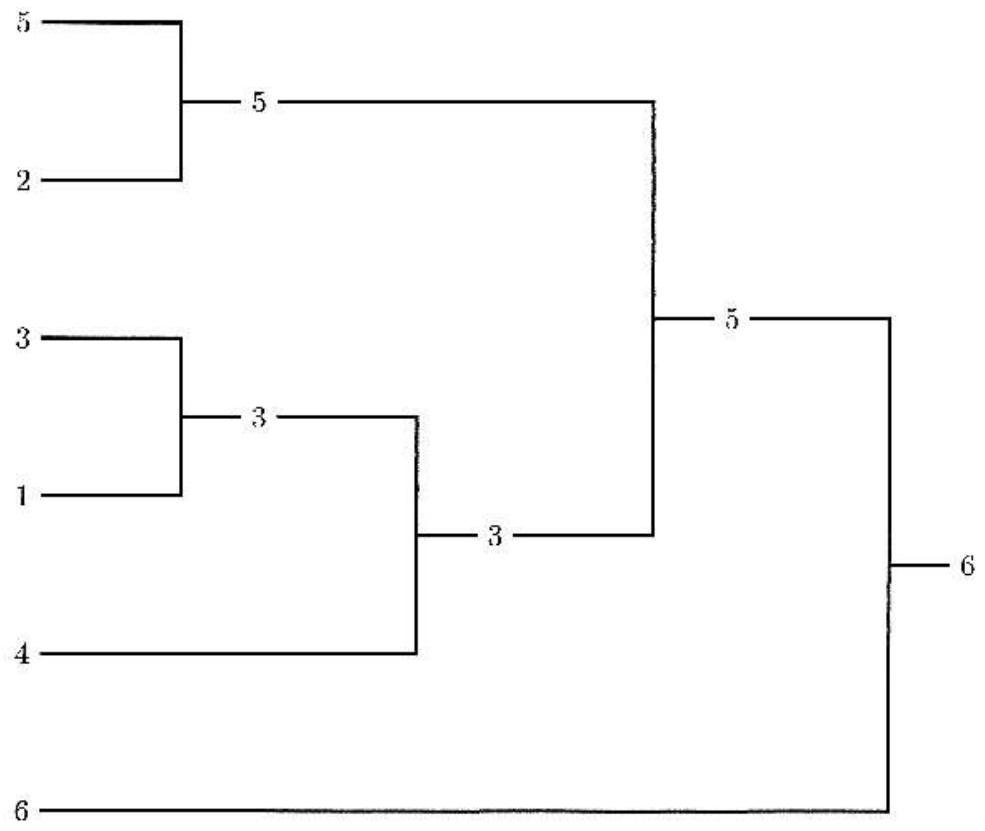
Figure 3 Déroulement du tournoi de la figure 1 en fonction de l'oracle de la figure 2.
Question 5 Écrire une fonction
Partie II. Vainqueurs Potentiels
Nous avons vu dans la Partic I qu'un tournoi
Question 6 Donner un oracle qui n'a qu'un seul vainqueur potentiel. Donner un oracle qui a plusicurs vainqueurs potentiels.
Pour calculer efficacement tous les vainqueurs potentiels de
Question 7 Écrire une fonction UnVainqueur
Question 8 Montrer que si
Question 9 Montrer quc, si un ensemble
Question 10 En utilisant les questions 7, 8, et 9, écrire la fonction VainqueursPotentiels (
Partie III. Pronostics
Dans cette partie, les oracles sont remplacés par des pronostics, qui donnent des chances (ou probabilités) de victoire plutôt que des certitudes. L'objectif de cette partie est de calculer la probabilité qu'a chaque joucur de remporter le tournoi.
La première difficulté réside dans le fait que l'issue d'un match ne peut, plus être déterminée avec certitude, et que donc plusieurs joucurs peuvent potentiellement participer à un même match. Il faut donc pouvoir calculer, pour chaque match, l'ensemble des joueurs susceptibles d'y participer.
Question 11 Écrire une fonction PremierJoueurPossible (
Nous considérons maintenant, que pour chaque match possible, les chances de victoire de chaque joueur sont données par des pronostics. Un pronoslic
Le but de la fin de cette partic est de calculer, à tournoi
- Si
est un premier joueur possible : ; - Si
est un second joneur possible : ; - Sinon :
.
Question 12 En utilisant les fonctions PremierJoueurPossible et une fonction analogue SecondJoueurPossible (que l'on s'abstiendra d'écrire), écrire une fonction
MiseAJour (
Question 13 Écrire une fonction ChancesDeVictoire (
