Ce sujet est découpé en deux parties totalement indépendantes toutes deux portant sur l'étude de réseaux sociaux : la première porte sur de la programmation en Python; la seconde porte sur l'interrogation de base de données à l'aide de requêtes en SQL.

A - Programmation en Python

Notations. On désignera par

l'ensemble des entiers de 0 à

Objectif. Le but de cette partie est de regrouper des personnes par affinité dans un réseau social. Pour cela, on cherche à répartir les personnes en deux groupes de sorte à minimiser le nombre de liens d'amitié entre les deux groupes. Une telle partition s'appelle une coupe minimale du réseau.

Complexité. La complexité, ou le temps d'exécution, d'un programme

(fonction ou procédure) est le nombre d'opérations élémentaires (addition, multiplication, affectation, test, etc...) nécessaires à l'exécution de

. Lorsque cette complexité dépend de plusieurs paramètres

, on dira que

a une complexité en

, lorsqu'il existe trois constantes

telles que la complexité de

soit inférieure ou égale à

, pour tout

Lorsqu'il est demandé de donner une certaine complexité, le candidat devra justifier cette dernière si elle ne se déduit pas directement de la lecture du code.

Implémentation. Dans ce sujet, nous adopterons la syntaxe du langage Python.
On rappelle qu'en Python, on dispose des opérations suivantes, qui ont toutes une complexité constante (car en Python, les listes sont en fait des tableaux de taille dynamique) :

[] crée une liste vide (c.-à-d. ne contenant aucun élément)
qui crée une liste (ou un tableau) à n éléments contenant tous la valeur contenue dans x . Par exemple, [1] renvoie le tableau (ou la liste) à 3 cases contenant toutes la même valeur 1.
len (liste) renvoie la longueur de la liste liste
liste [i] désigne le (i+1)-ème élément de la liste liste s'il existe et produit une erreur sinon (noter que le premier élément de la liste est liste[0]).
liste.append( x ) ajoute le contenu de x à la fin de la liste liste qui s'allonge ainsi d'un élément. Par exemple, après l'exécution de la suite d'instructions "liste = []; liste.append(2); liste.append([ 1,3 );", la variable liste a pour valeur la liste [2, [1, 3]]. Si ensuite on fait l'instruction liste[1].append([7,5]);, la variable liste a pour valeur la liste .
liste.pop() renvoie la valeur du dernier élément de la liste liste et l'élimine de la liste. Ainsi, après l'exécution de la suite d'instructions "listeA = [1, [2,3]]; listeB listeA.pop(); listeB. ; ", les trois variables listeA, listeB et c ont pour valeurs respectives [1], [2] et 3.
random.randint(a,b) renvoie un entier tiré (pseudo)aléatoirement et uniformément dans l'ensemble .
True et False sont les deux valeurs booléennes Vrai et Faux.

Important : L'usage de toute autre fonction sur les listes telle que liste.insert (

), liste.remove(

), liste.index(

), ou encore liste.sort(

) est rigoureusement interdit (ces fonctions devront être programmées explicitement si nécessaire).

Dans la suite, nous distinguerons fonction et procédure : les fonctions renvoient une valeur (un entier, une liste,...) tandis que les procédures ne renvoient aucune valeur.

Nous attacherons la plus grande importance à la lisibilité du code produit par les candidats; aussi, nous encourageons les candidats à introduire des procédures ou fonctions intermédiaires lorsque cela simplifie l'écriture.

Partie I. Réseaux sociaux

Structure de données. Nous supposerons que les individus sont numérotés de 0 à

où

est le nombre total d'individus. Nous représenterons chaque lien d'amitié entre deux individus i et j par une liste contenant leurs deux numéros dans un ordre quelconque, c.-à-d. par la liste

ou par la liste

indifféremment.

Un réseau social

entre

individus sera représenté par une liste reseau à deux éléments où :

reseau contient le nombre d'individus appartenant au réseau
reseau [1] = la liste non-ordonnée (et potentiellement vide) des liens d'amitié déclarés entre les individus
La figure 1 donne l'exemple d'un réseau social et d'une représentation possible sous la forme de liste. Chaque lien d'amitié entre deux personnes est représenté par un trait entre elles.

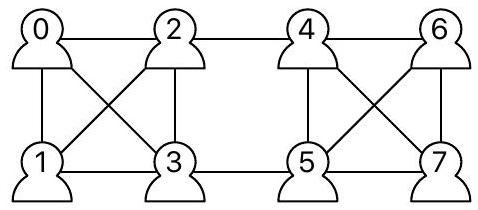
reseau = [ 8,
        [ [0,1], [1,3], [3,2], [2,0], [0,3], [2,1], [4,5],
            [5,7], [7,6], [6,4], [7,4], [6,5], [2,4], [5,3] ]
    ]

Figure 1 - Un réseau à 8 individus ayant 14 liens d'amitié déclarés et une de ses représentations possibles en mémoire sous forme d'une liste [ Nombre d'individus, liste des liens d'amitié ].

Question 1. Donner une représentation sous forme de listes pour chacun des deux réseaux sociaux ci-dessous :

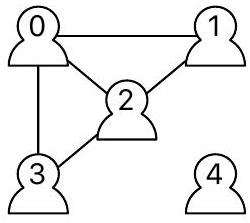
Réseau A

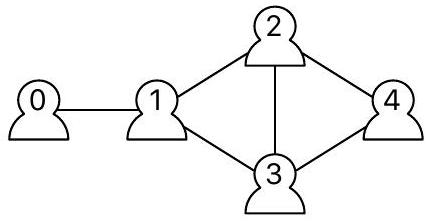
Réseau B

Question 2. Écrire une fonction creerReseauVide(n) qui crée, initialise et renvoie la représentation sous forme de liste du réseau à

individus n'ayant aucun lien d'amitié déclaré entre eux.

Question 3. Écrire une fonction estUnLienEntre(paire,

) où paire est une liste à deux éléments et i et j sont deux entiers, et qui renvoie True si les deux éléments contenus dans paire sont

dans un ordre quelconque ; et renvoie False sinon.

Question 4. Écrire une fonction sontAmis (reseau,

) qui renvoie True s'il existe un lien d'amitié entre les individus i et j dans le réseau reseau; et renvoie False sinon.

Quelle est la complexité en temps de votre fonction dans le pire cas en fonction du nombre

de liens d'amitié déclarés dans le réseau?

Question 5. Écrire une procédure declareAmis (reseau,i,j) qui modifie le réseau reseau pour y ajouter le lien d'amitié entre les individus i et j si ce lien n'y figure pas déjà.

Quelle est la complexité en temps de votre procédure dans le pire cas en fonction du nombre

de liens d'amitié déclarés dans le réseau?

Question 6. Écrire une fonction listeDesAmisDe (reseau,i) qui renvoie la liste des amis de i dans le réseau reseau.

Quelle est la complexité en temps de votre fonction dans le pire cas en fonction du nombre

de liens d'amitié déclarés dans le réseau?

Partie II. Partitions

Une partition en

groupes d'un ensemble

éléments consiste en

sous-ensembles disjoints non-vides

dont l'union est

, c.-à-d. tels que

et pour tout

. Par exemple

est une partition en trois groupes de

. Dans cette partie, nous implémentons une structure de données très efficace pour coder des partitions de

Le principe de cette structure de données est que les éléments de chaque groupe sont structurés par une relation filiale : chaque élément a un (unique) parent choisi dans le groupe et l'unique élément du groupe qui est son propre parent est appelé le représentant du groupe. On s'assure par construction que chaque élément i du groupe a bien pour ancêtre le représentant du groupe, c.-à-d. que le représentant du groupe est bien le parent du parent du parent etc. (autant de fois que nécessaire) du parent de l'élément i. La relation filiale est symbolisée par une flèche allant de l'enfant au parent dans la figure 2 qui présente un exemple de cette structure de données. Dans l'exemple de cette figure, 14 a pour parent 11 qui a pour parent 1 qui a pour parent 9 qui est son propre parent. Ainsi, 9 est le représentant du groupe auquel appartiennent

et 9 . Notons que ce groupe contient également 8,13 et 15 .

À noter que la représentation n'est pas unique (si l'on choisit un autre représentant pour un groupe et une autre relation filiale, on aura une autre représentation du groupe).

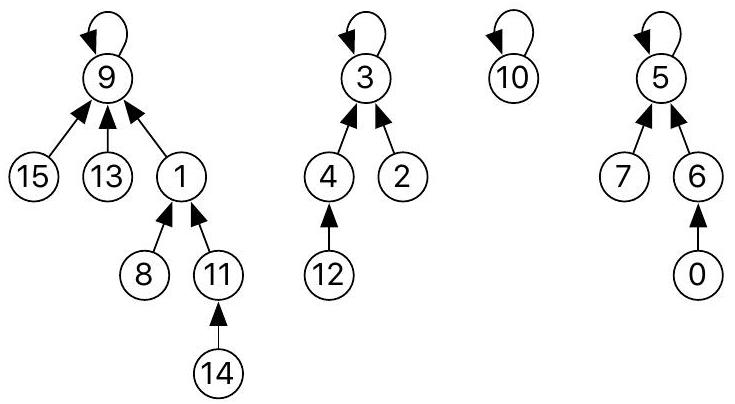
Figure 2 - Une représentation filiale de la partition suivante de 【16】 en quatre groupes :

dont les représentants respectifs sont 9,3 , 10 et 5 .

Pour coder cette structure, on utilise un tableau parent à

éléments où la case parent [i] contient le numéro du parent de i. Par exemple, les valeurs du tableau parent encodant la représentation filiale donnée dans la figure 2 sont :

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
parent	6	9	3	3	3	5	5	5	1	9	10	1	4	9	11	9

Question 7. Donner les valeurs du tableau parent encodant les représentations filiales des deux partitions de

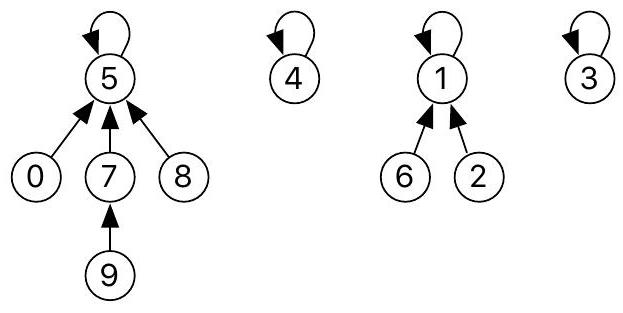
ci-dessous, et préciser les représentants de chaque groupe :

Représentation filiale A

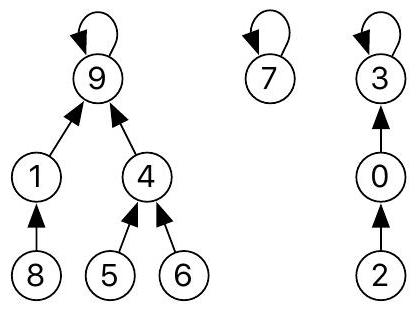
Représentation filiale B

Initialement, chaque élément de

est son propre représentant et la partition initiale consiste en

groupes contenant chacun un individu. Ainsi, initialement, parent

pour tout

Question 8. Écrire une fonction creerPartitionEnSingletons(n) qui crée et renvoie un tableau parent à n éléments dont les valeurs sont initialisées de sorte à encoder la partition de

groupes d'un seul élément.

Nous sommes intéressés par deux opérations sur les partitions :

Déterminer si deux éléments appartiennent au même groupe dans la partition.
Fusionner deux groupes pour n'en faire plus qu'un. Par exemple, la fusion des groupes et dans la partition de donnée en exemple au tout début de cette partie donnera la partition en deux groupes et où .
Question 9. Écrire une fonction representant (parent,i) qui utilise le tableau parent pour trouver et renvoyer l'indice du représentant du groupe auquel appartient i dans la partition encodée par le tableau parent.

Quelle est la complexité dans le pire cas de votre fonction en fonction du nombre total

d'éléments? Donnez un exemple de tableau parent à

éléments qui atteigne cette complexité dans le pire cas.

Pour réaliser la fusion de deux groupes désignés par l'un de leurs éléments i et j respectivement, on applique l'algorithme suivant :

Calculer les représentants et des deux groupes contenant et respectivement.
Faire parent [p] = q.

La figure 3 présente la structure filiale obtenue après la fusion des groupes contenant respectivement 6 et 14 de la figure 2.

Question 10. Écrire une procédure fusion (parent,

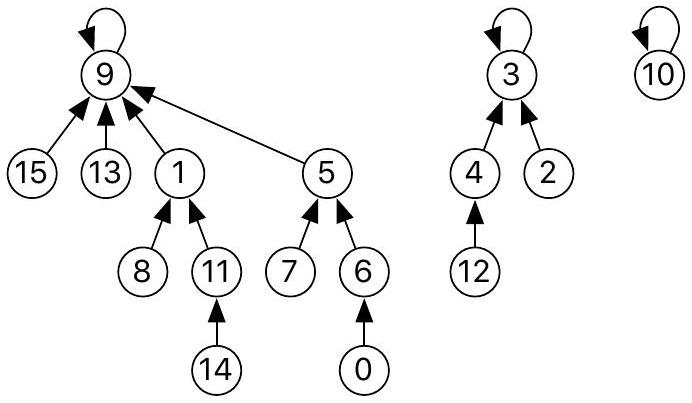
) qui modifie le tableau parent pour fusionner les deux groupes contenant

respectivement.

Figure 3 - Représentation filiale obtenue après la fusion des groupes contenant respectivement 6 et 14 de la figure 2 .

Pour l'instant, la structure de données n'est pas très efficace comme le montre la question suivante.

Question 11. Proposer une suite de (

) fusions dont l'exécution à partir de la partition en

singletons de

, nécessite de l'ordre de

opérations élémentaires.

Pour remédier à cette mauvaise performance, une astuce consiste à compresser la relation filiale après chaque appel à la fonction representant(parent,i). L'opération de compression consiste à faire la chose suivante : si

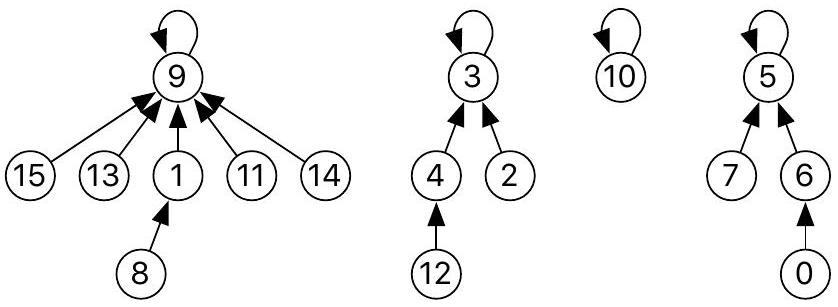
est le résultat de l'appel à la fonction representant(parent,i), modifier le tableau parent de façon à ce que chaque ancêtre (c.-à-d. parent de parent ... de parent) de i, i y compris, ait pour parent direct p. Noter bien que même si un appel à representant(parent,i) renvoie le représentant de i elle modifie également le tableau parent. Si l'on reprend l'exemple de la figure 2, le résultat de l'appel representant (parent, 14) est 9 , que l'on a calculé en remontant les ancêtres successifs de 14 : 11, 1 puis 9 . L'opération de compression consiste alors à donner la valeur 9 aux cases d'indices 14, 11, et 1 du tableau parent. La structure filiale obtenue après l'opération de compression menée depuis 14 est illustrée dans la figure 4.

Figure 4 - Résultat de la compression depuis 14 dans la représentation filiale de la figure 2.

Question 12. Modifier votre fonction representant (parent,i) pour qu'elle modifie le tableau parent pour faire pointer directement tous les ancêtres de i vers le représentant de i une fois qu'il a été trouvé.

En quoi cette optimisation de la structure filiale peut-elle être considérée comme "gratuite" du point de vue de la complexité?

Afin d'afficher de manière lisible la partition codée par un tableau parent, on souhaite calculer à partir du tableau parent la liste des listes des éléments des différents groupes. Une sortie possible pour le tableau parent correspondant à la figure 2 serait :

[ [ 15, 8, 1, 9, 11, 13, 14 ],
    [ 4, 3, 2, 12],
    [ 7, 5, 6, 0],
    [ 10 ] ]

Question 13. Écrire une fonction listeDesGroupes (parent) qui renvoie la liste des différents groupes codés par le tableau parent sous la forme d'une liste des listes des éléments des différents groupes.

Partie III. Algorithme randomisé pour la coupe minimum

Revenons à présent à notre objectif principal : Trouver une partition des individus d'un réseau social en deux groupes qui minimise le nombre de liens d'amitiés entre les deux groupes.

Pour résoudre ce problème nous allons utiliser l'algorithme randomisé suivant :
Entrée : un réseau social à

individus

Créer une partition en singletons de
Initialement aucun lien d'amitié n'est marqué
Tant que la partition contient au moins trois groupes et qu'il reste des liens d'amitié non-marqués dans le réseau faire :
(a) Choisir un lien uniformément au hasard parmi les liens non-marqués du réseau, notons-le .
(b) Si i et j n'appartiennent pas au même groupe dans la partition , fusionner les deux groupes correspondants
(c) Marquer le lien .
Si contient groupes, faire fusions pour obtenir deux groupes.
Renvoyer la partition .

La figure 5 présente une exécution possible de cet algorithme randomisé sur le réseau de la figure 1.

Question 14. Écrire une fonction coupeMinimumRandomisee(reseau) qui renvoie le tableau parent correspondant à la partition calculée par l'algorithme ci-dessus.

Indication. Au lieu de marquer explicitement les liens déjà vus, on pourra avantageusement les positionner à la fin de la liste non-ordonnée des liens du réseau et ainsi pouvoir tirer simplement les liens au hasard parmi ceux placés au début de la liste.

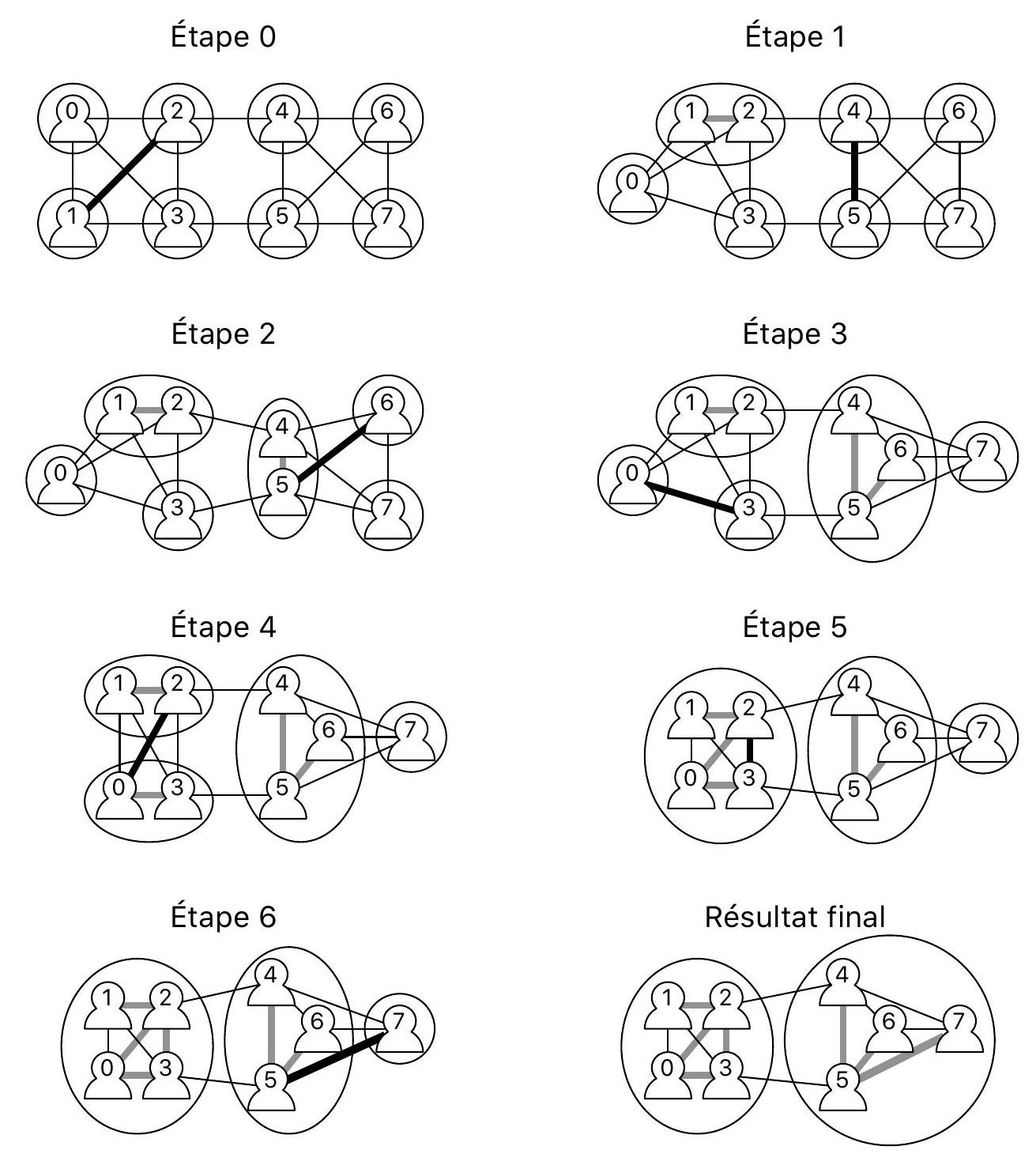
Figure 5 - Une exécution de l'algorithme randomisé sur le réseau de la figure 1 où les liens sélectionnés aléatoirement sont dans l'ordre :

. Les liens représentés en noir épais sont les liens sélectionnés au hasard à l'étape courante; les liens épais et grisés sont les liens marqués par l'algorithme; les ronds représentent la partition à l'étape courante.

Quelle est la complexité de votre procédure en fonction de

, où

est le nombre de liens d'amitié déclarés dans le réseau et où

désigne la complexité d'un appel à la fonction representant?

Question 15. Écrire une fonction tailleCoupe(reseau, parent) qui calcule le nombre de liens entre les différents groupes de la partition représentée par parent dans le réseau reseau.

On peut démontrer que cet algorithme renvoie une coupe de taille minimum avec une probabilité supérieure à

, ce qui fait que la meilleure parmi

exécutions indépendantes de cet algorithme est effectivement minimum avec probabilité supérieure à

La structure de données filiale avec compression pour les partitions est particulièrement efficace aussi bien en pratique qu'en théorie. En effet, la complexité de

opérations est de

opérations élémentaires où

est l'inverse de la fonction d'Ackermann, une fonction qui croit extrêmement lentement vers l'infini (par exemple

B - Programmation SQL

Une représentation simplifiée, réduite à deux tables, de la base de données d'un réseau social est donnée dans la figure 6 .

id	nom	prenom
1	Potter	Harry
2	Granger	Hermione

id1	id2
1	2
2	1

Figure 6 - Schéma de la base de données du réseau social

La table INDIVIDUS répertorie les individus et contient les colonnes

id (clé primaire), un entier identifiant chaque individu;
nom, une chaîne de caractères donnant le nom de famille de l'individu;
prenom, une chaîne de caractères donnant le prénom de l'individu.

La table LIENS répertorie les liens d'amitiés entre individus et contient les colonnes

id1, entier identifiant le premier individu du lien d'amitié;
id2, entier identifiant le second individu du lien d'amitié.

On supposera par ailleurs que pour tout couple

dans la table LIENS, le couple

est également présent dans la table (contrairement à la partie précédente de cet énoncé).

Question 16. Écrire une requête SQL qui renvoie les identifiants des amis de l'individu d'identifiant x .

Question 17. Écrire une requête SQL qui renvoie les (noms,prénoms) des amis de l'individu d'identifiant x .

Question 18. Écrire une requête SQL qui renvoie les identifiants des individus qui sont amis avec au moins un ami de l'individu d'identifiant x .