Version interactive avec LaTeX compilé
COMPOSITION D'INFORMATIQUE - B - (XEC)
(Durée : 2 heures)
L'utilisation des calculatrices n'est pas autorisée pour cette épreuve.
Le langage de programmation choisi par le candidat doit être spécifié en tête de la copie.
Le langage de programmation choisi par le candidat doit être spécifié en tête de la copie.
Grands rectangles
Ce sujet porte sur la détection de zones rectangulaires monochromatiques dans une image. Imaginons par exemple une image en noir et blanc, le problème est d'en trouver la plus grande zone noire. Ces zones monochromatiques peuvent être représentées de manière compacte en retenant les cordonnées des coins et la couleur interne. En décomposant une image selon ces grands rectangles, il est possible de la compresser efficacement, les zones monochromatiques pouvant être représentées de manière très compacte.
La complexité, ou le temps d'exécution, d'un programme
Partie I. Recherche unidimensionnelle
Dans cette partie, nous allons étudier le problème de reconnaissance de forme sur des tableaux unidimensionnels. Nous supposerons donnés un entier
Dans cette partie nous utiliserons le tableau suivant comme exemple :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
Question 1 Écrire une fonction nombreZerosDroite
Sur le tableau exemple précédent, en prenant comme indice
Il est maintenant possible de réaliser un algorithme de complexité optimale utilisant la fonction précédente. En voici une brève description. Parcourons le tableau de gauche à droite et à chaque début de plage de 0 contigüs, nous calculons la taille de cette plage puis repartons juste après elle. Ayant ainsi calculé la taille de toutes les plages de 0 il suffit de retenir celle de taille maximale. Sur l'exemple précédent, on part de l'indice 1 qui est un début de plage de 0 de taille 2. Nous continuons donc à chercher le prochain début de plage à partir de l'indice
Question 2 Écrire une fonction nombreZerosMaximum
Partie II. De la 1D vers la 2D
Cette partie consiste à développer un algorithme efficace pour détecter un rectangle d'aire maximale rempli de 0 dans un tableau bidimensionnel. Par mesure de simplification, nous travaillerons sur des tableaux carrés et nous supposerons donné un tableau tab2 de taille
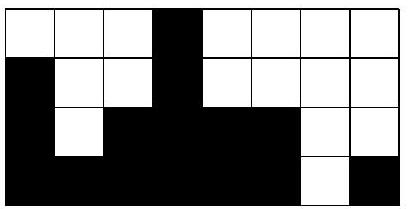
Nous utiliserons le tableau suivant comme exemple :
|
|
|
|
|
|
|
|
|
|
|
|
0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
|
|
0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
|
|
1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
|
|
0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
|
|
0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
|
|
0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
|
|
0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
|
|
0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
Méthode naïve La première méthode proposée consiste à prendre une cellule (
Question 3 Écrire une fonction rectangleHautDroit
Question 4 Expliquer comment trouver naïvement un rectangle d'aire maximale rempli de 0 en utilisant la fonction rectangleHautDroit. Quelle serait la complexité de cette approche en fonction de
Un peu de précalcul Notre algorithme parcourt de nombreuses fois les même cases afin de vérifier la présence d'un 0 ou d'un 1 . Nous allons donc effectuer avant notre algorithme un précalcul de certaines valeurs ce qui nous permettra, dans la partie III, d'accélérer les fonctions précédentes.
Pour chaque cellule (
|
|
|
|
|
|
|
|
|
|
|
|
1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
|
|
2 | 2 | 1 | 1 | 0 | 2 | 2 | 0 |
|
|
0 | 3 | 2 | 2 | 1 | 3 | 3 | 0 |
|
|
1 | 0 | 3 | 3 | 2 | 4 | 4 | 0 |
|
|
2 | 1 | 0 | 0 | 3 | 5 | 5 | 0 |
|
|
3 | 2 | 0 | 1 | 4 | 6 | 6 | 0 |
|
|
4 | 0 | 0 | 0 | 5 | 0 | 7 | 0 |
|
|
5 | 1 | 0 | 0 | 6 | 1 | 8 | 0 |
Question 5 Écrire une fonction colonneZeros
Question 6 Quelle est la complexité de la fonction colonneZeros?
Partie III. Algorithme optimisé
Rectangle d'aire maximale dans un histogramme Une nouvelle étape dans notre algorithme réside dans la résolution du problème du calcul d'un rectangle d'aire maximale inscrit dans un histogramme. Nous supposerons donné un histogramme c'est à dire un tableau histo de taille
|
|
|
|
|
|
|
|
|
|
| histo
|
3 | 1 | 2 | 4 | 2 | 2 | 0 | 1 |
L'idée est de calculer un indice
Notons que
Nous pourrions calculer les valeurs
On calcule successivement les valeurs de
Répéter :
- Si
alors affecter et terminer. - Sinon :
- Si histo
histo alors affecter et terminer. - Sinon histo
histo alors affecter et continuer.
Question 7 Montrer que l'algorithme précédent calcule correctement les valeurs de
On supposera donnée une fonction calculeL(histo,
Question 8 Justifier que pour tout
Question 9 Soit un rectangle d'aire maximale inscrit dans l'histogramme. Supposons que ce rectangle commence à l'indice
Question 10 En déduire une fonction plusGrandRectangleHistogramme(histo, n) qui calcule et renvoie l'aire d'un plus grand rectangle inscrit dans l'histogramme. Donner la complexité de votre fonction plusGrandRectangleHistogramme.
Partie IV. Conclusion
En revenant au problème initial du calcul d'un rectangle de 0 d'aire maximale dans une matrice en deux dimensions, remarquer que chaque ligne du tableau col calculé par la fonction colonneZeros de la question 5 peut être interprétée comme un histogramme.
En utilisant cette analogie, il est possible de proposer une méthode efficace de résolution du problème.
Question 11 Écrire la fonction rectangleToutZero
Question 12 Quelle est la complexité de votre fonction?
