Version interactive avec LaTeX compilé
A2025 - PHYSIQUE II PSI
Concours commun
Mines-Ponts
Mines-Ponts
ÉCOLE NATIONALE DES PONTS et CHAUSSÉES, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL.
CONCOURS 2025
DEUXIÈME ÉPREUVE DE PHYSIQUE
Durée de l'épreuve : 4 heures
L'usage de la calculatrice ou de tout dispositif électronique est interdit.
L'usage de la calculatrice ou de tout dispositif électronique est interdit.
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE II - PSI
L'énoncé de cette épreuve comporte 9 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Oscillations mécaniques et électriques
Il est souvent plus simple lorsque l'on veut étudier expérimentalement, au laboratoire, le comportement d'un oscillateur mécanique en fonction de ses paramètres, d'en réaliser une version électronique plutôt qu'une version mécanique. Les réglages sont plus fins car plus nombreux et la possibilité d'acquisition directe des signaux en divers points du circuit électrique permet la mise au point et l'adaptation de ce dernier à la richesse des oscillations mécaniques. Après avoir étudié un oscillateur mécanique et entrepris sa modélisation numérique dans la première partie, nous construirons progressivement dans la seconde son équivalent électronique. Dans tout le problème un point surmontant une fonction désigne sa dérivée temporelle :
I Oscillateur mécanique
On considère un ressort d'extrémités
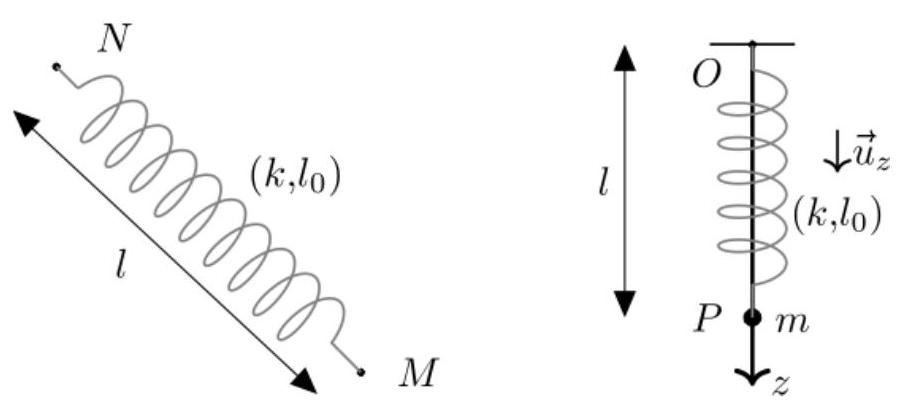
Figure 1 - Ressort et oscillateur vertical
On suppose que le mouvement du point matériel
Dans tout le problème, le ressort reste dans son domaine élastique de fonctionnement associé à une force de rappel proportionnelle à son allongement. Le champ de pesanteur
On suppose tout d'abord que le ressort a une masse
Dans tout le problème, le ressort reste dans son domaine élastique de fonctionnement associé à une force de rappel proportionnelle à son allongement. Le champ de pesanteur
On suppose tout d'abord que le ressort a une masse
-
- Établir l'expression de l'énergie potentielle élastique
du ressort dont on prendra l'origine lorsque la longueur du ressort est égale à sa longueur à vide. On exprimera en fonction de et .
- Établir l'expression de l'énergie potentielle élastique
-
- Établir, en fonction de
et , l'expression de l'énergie potentielle de pesanteur du point matériel dont on prendra l'origine en .
- Établir, en fonction de
-
- En déduire l'expression de l'énergie mécanique
du point matériel de masse dans le référentiel galiléen en fonction notamment de .
- En déduire l'expression de l'énergie mécanique
-
- Établir l'équation différentielle du mouvement du point matériel
vérifiée par dans le référentiel galiléen .
- Établir l'équation différentielle du mouvement du point matériel
-
- Résoudre l'équation différentielle obtenue à la question précédente en supposant qu'à
, le point matériel est lâché sans vitesse initiale de la position . On fera apparaître une pulsation .
Quelle condition doit-on imposer àpour que le point matériel ne heurte pas le support fixe où est suspendu le ressort? On exprimera cette condition en fonction de et . Qualifier le mouvement observé : tracer l'allure de en fonction de .
Donner l'expression de la périodedu mouvement du point matériel et calculer sa valeur numérique pour et .
- Résoudre l'équation différentielle obtenue à la question précédente en supposant qu'à
Dans les 6 questions suivantes, on tient compte de la masse
-
- Établir l'expression de l'énergie potentielle de pesanteur
associée au ressort en fonction de et .
- Établir l'expression de l'énergie potentielle de pesanteur
-
- Établir l'expression de l'énergie cinétique
du ressort en fonction de et .
- Établir l'expression de l'énergie cinétique
-
- En déduire l'expression de l'énergie mécanique
du système constitué par le point matériel de masse et le ressort de masse dans le référentiel galiléen en fonction de et .
- En déduire l'expression de l'énergie mécanique
-
- Établir l'équation différentielle du mouvement du point matériel
vérifiée par dans le référentiel galiléen . Commenter.
- Établir l'équation différentielle du mouvement du point matériel
-
- Résoudre l'équation différentielle obtenue à la question précédente en supposant qu'à
, le point matériel est lâché sans vitesse initiale de la position . On fera apparaître une pulsation .
Qualifier le mouvement observé en supposant que le point matérielne heurte pas le support fixe.
Déterminer l'expression de la périodedu mouvement du point matériel en fonction de et puis calculer sa valeur numérique pour , et (on pourra utiliser l'approximation ).
- Résoudre l'équation différentielle obtenue à la question précédente en supposant qu'à
-
- Quelle condition doit satisfaire
pour que l'écart relatif entre et ne dépasse pas ? On fera l'application numérique dans les conditions de la question précédente.
Le point matérielde masse est maintenant astreint à se déplacer, sans frottement, horizontalement sur une glissière parfaite qui se confond avec la droite ( ) (cf figure 2). Le ressort précédent, dont on suppose la masse nulle dans toute la suite du problème, est toujours accroché par son extrémité au point fixe dans le référentiel galiléen d'étude et par son extrémité au point matériel :
- Quelle condition doit satisfaire
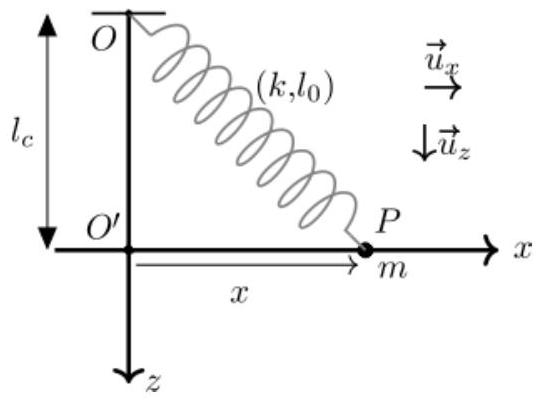
Figure 2 - Oscillateur horizontal
On se place maintenant dans le système de coordonnées cartésiennes (
-
- En fonction du paramètre
, discuter des positions d'équilibre du point et de leur stabilité respective : on exprimera les abscisses d'équilibre associées en fonction des données et on donnera les allures correspondantes de en fonction de en précisant les valeurs remarquables.
- En fonction du paramètre
-
- Dans quel cas peut-on parler de barrière de potentiel? Préciser sa hauteur
en fonction des données.
- Dans quel cas peut-on parler de barrière de potentiel? Préciser sa hauteur
-
- Établir l'équation différentielle du mouvement du point matériel
vérifiée par dans le référentiel galiléen .
Que représente physiquementen termes de force?
- Établir l'équation différentielle du mouvement du point matériel
-
- Transformer l'équation différentielle du mouvement en 2 équations différentielles d'ordre 1 en variables
et .
En introduisant les estimationsde et de aux instants pour où désigne le pas de discrétisation temporelle, former les 2 relations exprimant et en fonction de et déduites de la méthode d'Euler explicite.
Quelles valeurs doit-on donner pourà et ?
Pouret , on effectue la résolution numérique de l'équation différentielle du mouvement pour déterminer et en fonction de pour 2 conditions initiales A et B différentes. Les résultats sont présentés sur la figure 3.
- Transformer l'équation différentielle du mouvement en 2 équations différentielles d'ordre 1 en variables
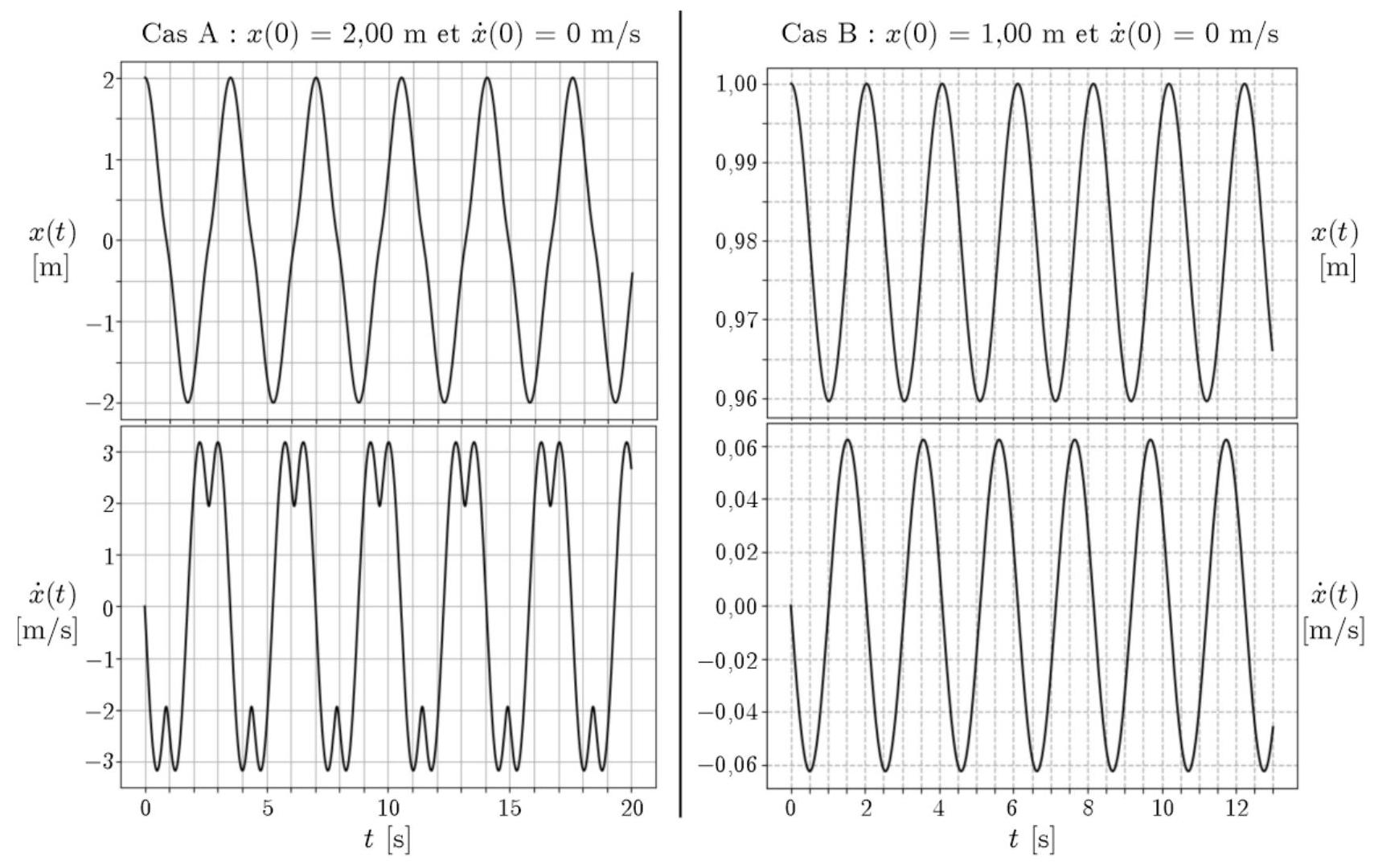
Figure 3 - Solutions numériques pour deux conditions initiales distinctes
-
- Comparer le plus précisément possible la nature du mouvement dans les 2 cas.
-
- Dans le cas B, établir une expression approchée de la valeur moyenne
des oscillations (en fonction de et ) et de leur période en fonction de et .
Effectuer les applications numériques et comparer les résultats aux valeurs lues sur la figure 3. Conclure sur les approximations effectuées.
- Dans le cas B, établir une expression approchée de la valeur moyenne
-
- Les 2 cas A et B correspondent à deux types de mouvements différents du point
. Dans le cas où les conditions initiales sont du type et , établir la condition que doit vérifier pour que l'on soit dans le cas A .
En conservant les valeurset , on a représenté sur la figure 4 l'allure de en fonction de dans les cas (à gauche) et (à droite).
- Les 2 cas A et B correspondent à deux types de mouvements différents du point
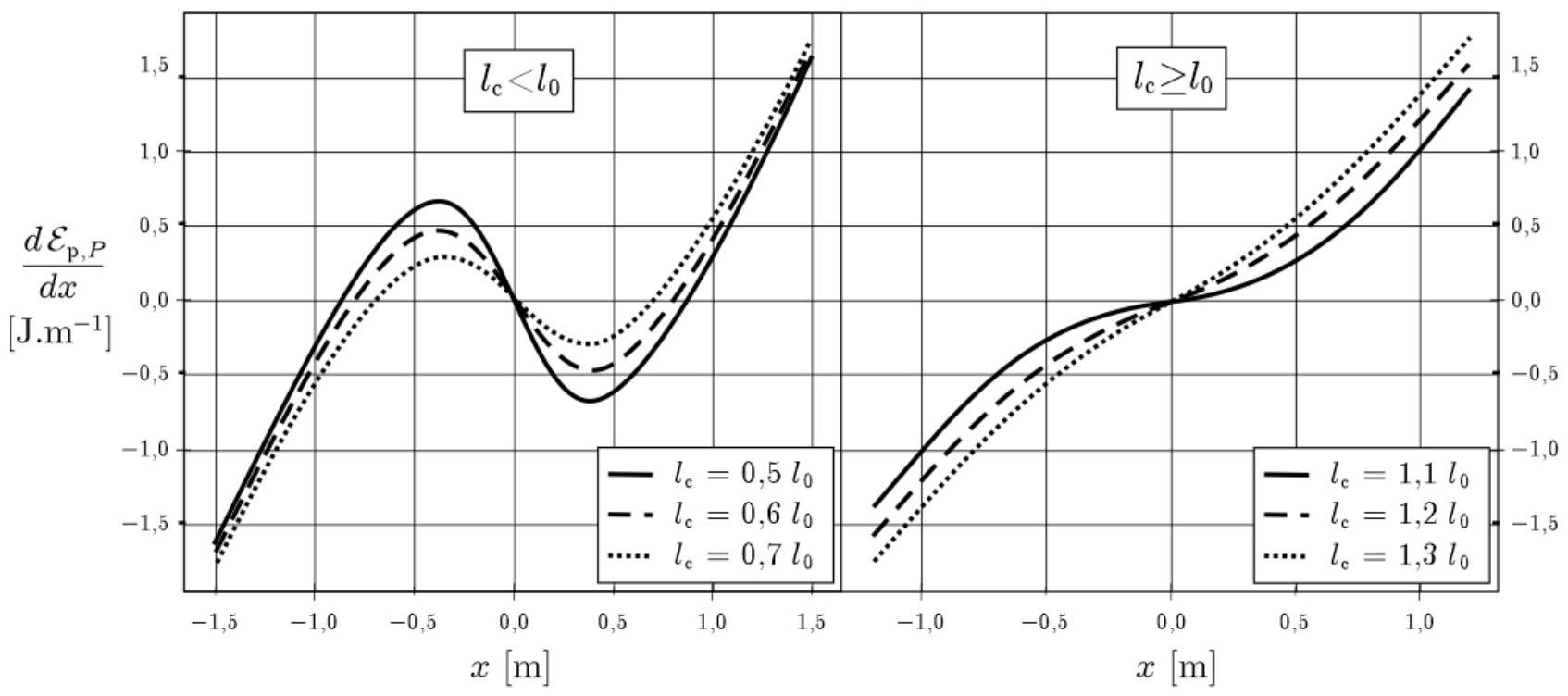
Figure 4 - Représentation graphique de la dérivée de l'énergie potentielle de pesanteur de
On suppose pouvoir modéliser la fonction
-
- Commenter cette affirmation et préciser en fonction de la valeur de
les signes des constantes et .
Réécrire alors l'équation différentielle du mouvement du point matérielvérifiée par . Cette équation est connue sous le nom d'équation de Duffing non amortie.
- Commenter cette affirmation et préciser en fonction de la valeur de
II Oscillateur électrique
Dans la suite du problème, nous allons étudier le circuit électronique présenté sur la figure 5 visant à simuler l'oscillateur mécanique décrit dans la partie précédente. Les trois amplificateurs linéaires intégrés (ALI) nommés (A1), (A2) et (A3) sont supposés idéaux, de gain infini et fonctionnant en régime linéaire. On notera
-
- Établir l'équation différentielle vérifiée par la tension
définie sur le circuit de la figure 5.
À quelle situation mécanique ce circuit correspond-il?
- Établir l'équation différentielle vérifiée par la tension
-
- On suppose, uniquement dans cette question, que l'on place dans le circuit de la figure 5 une résistance
en parallèle sur le condensateur de capacité . Établir l'équation différentielle vérifiée par la tension . À quelle situation mécanique ce circuit correspond-il?
- On suppose, uniquement dans cette question, que l'on place dans le circuit de la figure 5 une résistance
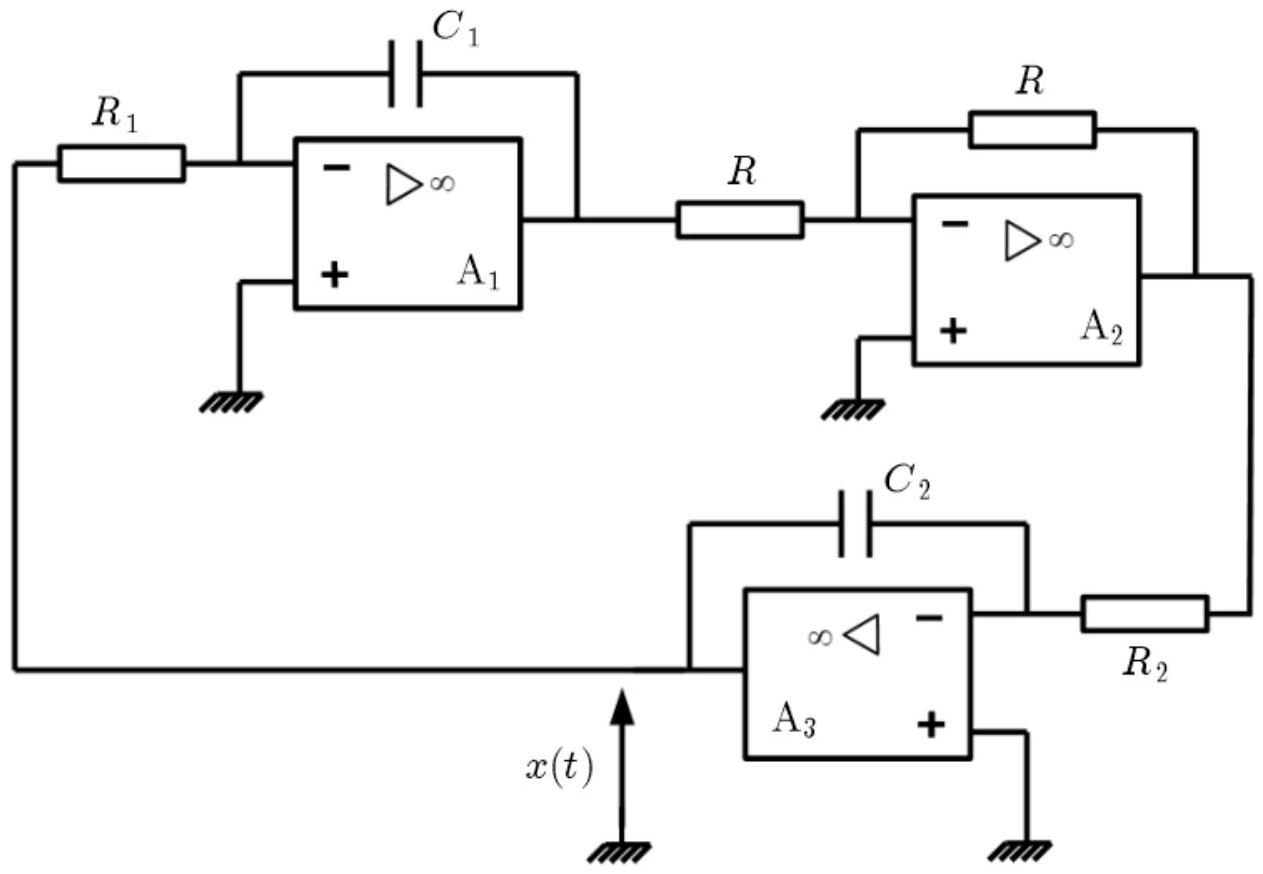
Figure 5 - Oscillateur électronique
On considère la diode
On réalise avec une diode
On réalise avec une diode
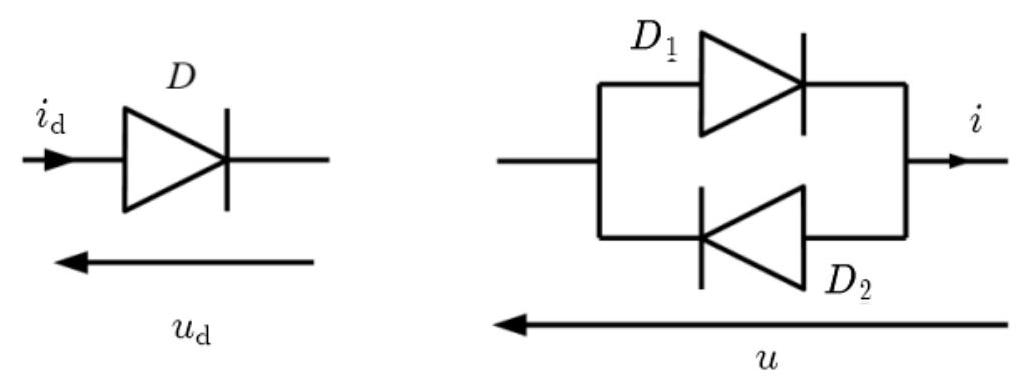
Figure 6 - Description d'une diode (à gauche) et d'un montage à diode en tête-bèche (à droite)
-
- Tracer la caractéristique courant-tension
de la diode .
- Tracer la caractéristique courant-tension
Établir la caractéristique courant-tension
On considère le montage de la figure 7 réalisé avec un amplificateur linéaire intégré nommé (A4) supposé idéal, de gain infini et fonctionnant en régime linéaire. On suppose que les deux diodes
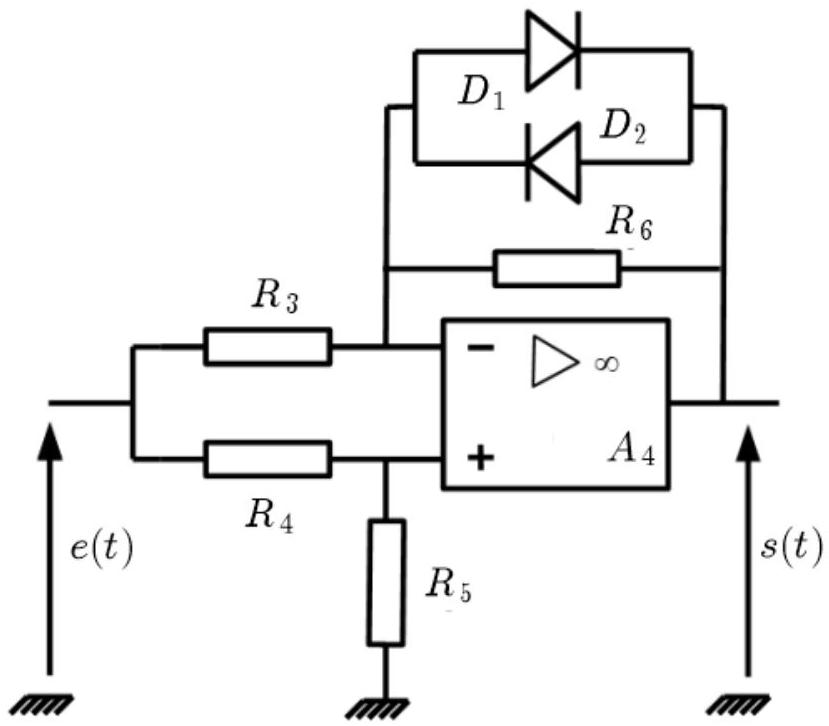
Figure 7 - Circuit à diodes
-
- Établir la caractéristique
du montage de la figure 7. Cette caractéristique fait apparaitre 3 zones différentes : dans chacune d'entre elles, on précisera l'expression de et la condition que doit vérifier pour être dans la zone considérée en fonction des résistances et de la tension seuil .
. Pour , tracer la caractéristique : on précisera la valeur numérique des pentes des droites apparaissant sur le tracé ainsi que l'expression des coordonnées des points remarquables en fonction de : extrema, intersections avec l'axe des abscisses.
- Établir la caractéristique
Grâce à un montage en laboratoire, on a pu relever le tracé de la caractéristique
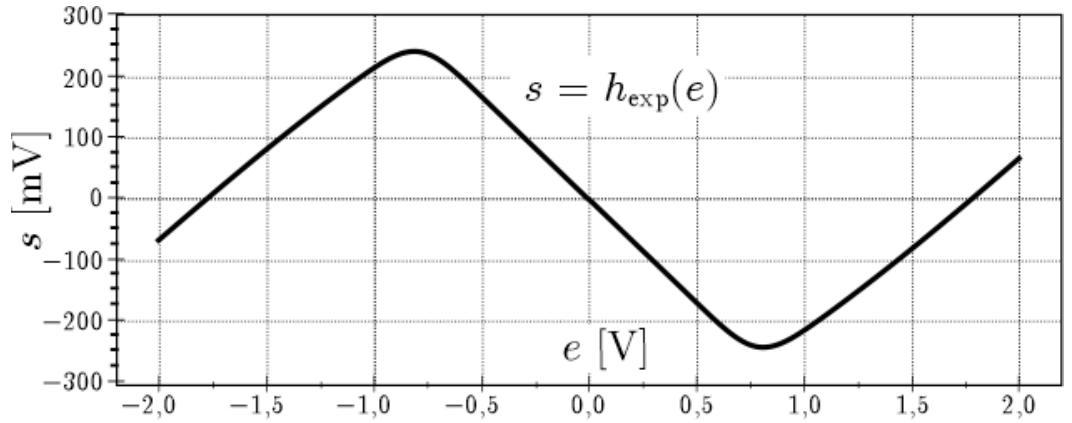
Figure 8 - Relevé expérimental de la caractéristique
-
- Comparer précisément le tracé
de la question 25 avec le relevé expérimental et proposer une interprétation pour les écarts entre les tracés.
Estimer la valeur numérique de la tension seuilen supposant que les valeurs numériques des abscisses des points d'intersection du relevé expérimental avec l'axe des abscisses s'identifient aux expressions établies dans la question 25.
- Comparer précisément le tracé
On suppose pouvoir modéliser la fonction
-
- Déterminer les valeurs numériques de
et fixées par le relevé expérimental de la figure 8.
- Déterminer les valeurs numériques de
On insère maintenant le circuit à diodes de la figure 7, d'entrée
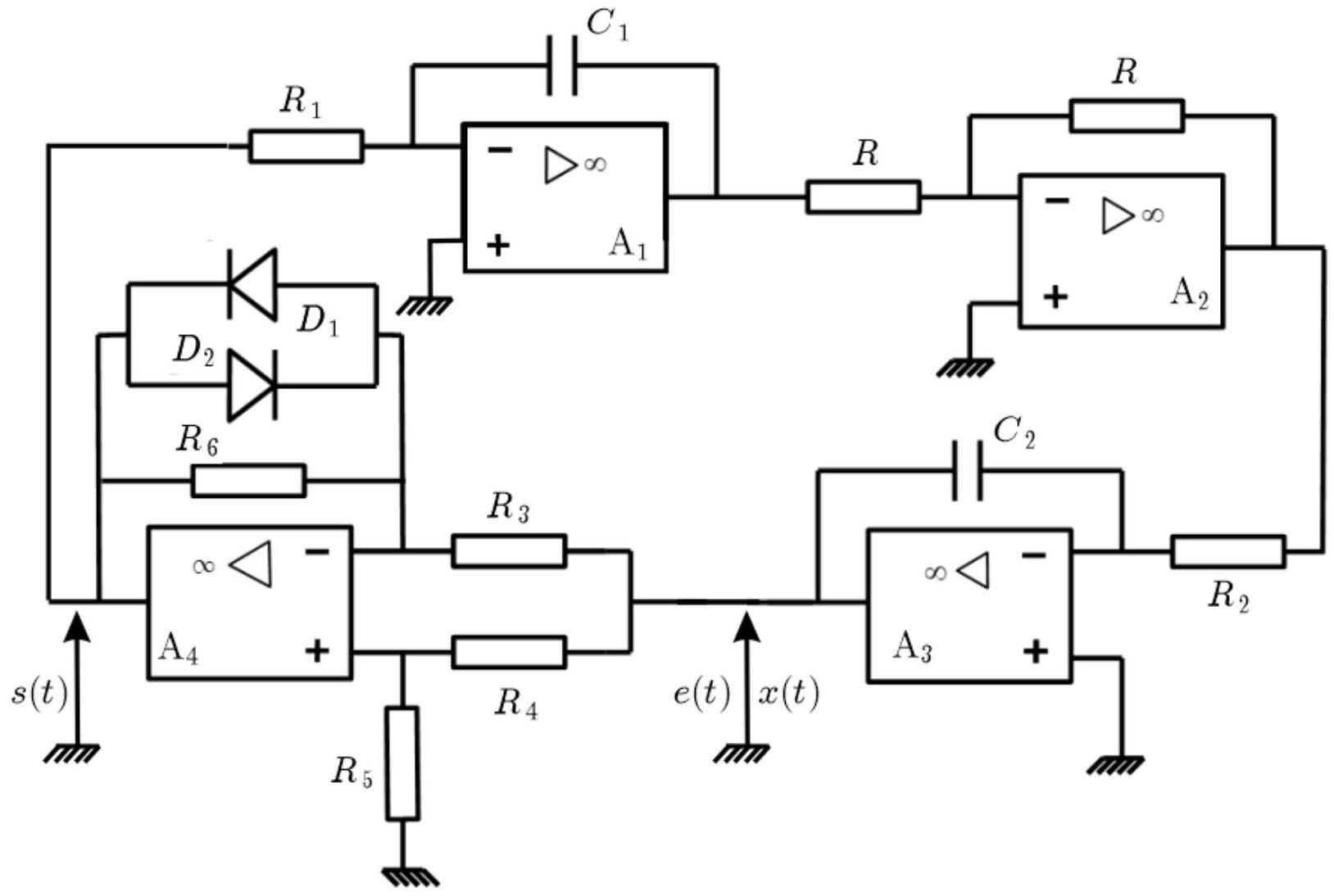
Figure 9 - Circuit complet
-
- Établir l'équation différentielle vérifiée par la tension
du circuit de la figure 9 en fonction de et . Commenter.
Si, quelle condition doit vérifier pour se trouver dans une situation semblable à celle de la question 20 avec ? On expliquera le raisonnement.
On souhaite relever expérimentalement sur le montage de la figure 9 des courbes analogues à celles de l'oscillateur mécanique données sur la figure 3.
- Établir l'équation différentielle vérifiée par la tension
-
- Comment avoir accès expérimentalement à une tension proportionnelle à
?
- Comment avoir accès expérimentalement à une tension proportionnelle à
Comment imposer expérimentalement des conditions initiales
Lorsque l'on réalise le montage de la figure 9 , les allures des tensions
On se propose d'interpréter ce fait expérimental en considérant que les amplificateurs linéaires intégrés utilisés ne sont pas idéaux car ils présentent des courants d'entrée d'intensités
Il faut alors reprendre l'analyse du montage de la figure 9 en changeant la modélisation des ALI. Pour ce faire, on peut par exemple introduire deux générateurs de courant comme dans le schéma de la figure 10 où la modélisation de l'ALI réel (A1) apparait entourée par des pointillés.
Lorsque l'on réalise le montage de la figure 9 , les allures des tensions
On se propose d'interpréter ce fait expérimental en considérant que les amplificateurs linéaires intégrés utilisés ne sont pas idéaux car ils présentent des courants d'entrée d'intensités
Il faut alors reprendre l'analyse du montage de la figure 9 en changeant la modélisation des ALI. Pour ce faire, on peut par exemple introduire deux générateurs de courant comme dans le schéma de la figure 10 où la modélisation de l'ALI réel (A1) apparait entourée par des pointillés.
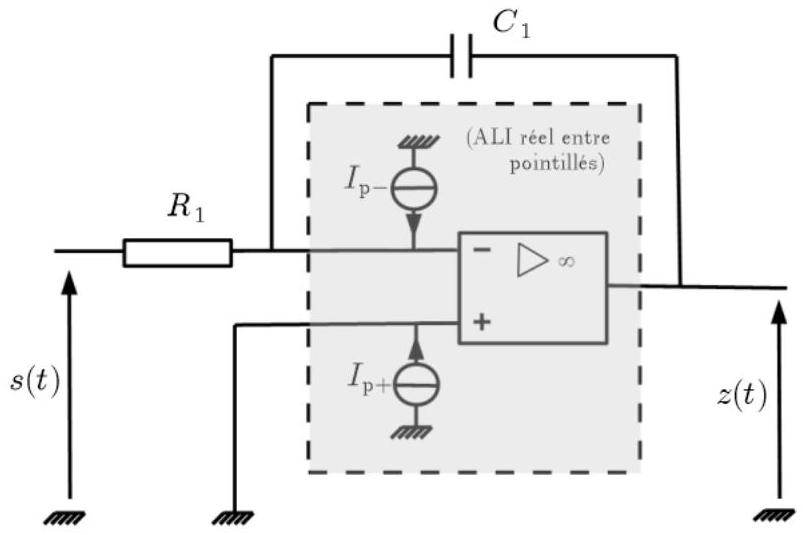
Figure 10 - Circuit avec la modélisation d'un ALI réel
-
- En supposant les intensités
et constantes dans le temps, établir l'équation différentielle reliant les tensions et .
Résoudre cette équation enpour en supposant le condensateur de capacité initialement déchargé.
En déduire pourquoi les allures observées des tensionset ne sont pas celles attendues; préciser le phénomène observé.
On place dorénavant une résistanceen parallèle avec le condensateur de capacité .
- En supposant les intensités
-
- Établir l'équation différentielle reliant les tensions
et et donner la forme générale (sans préciser toutes les constantes) de en régime établi pour .
En déduire l'intérêt de placer une résistanceen parallèle sur le condensateur et une résistance en parallèle sur le condensateur du circuit de la figure 9 .
Après avoir placé les deux résistances identiques, en parallèle sur les condensateurs et du circuit de la figure 9 réalisé avec et , on obtient les relevés expérimentaux présentés sur la figure 11.
- Établir l'équation différentielle reliant les tensions
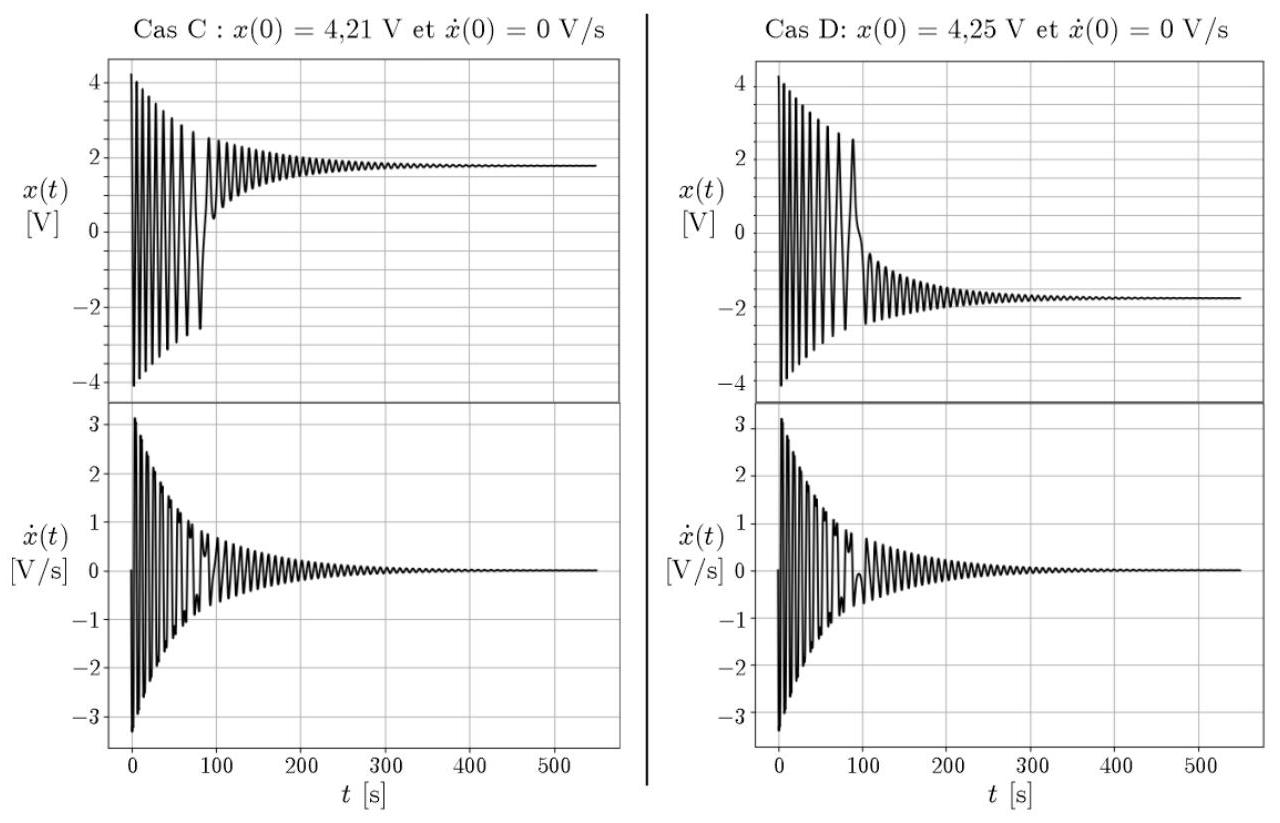
Figure 11 - Relevés expérimentaux pour deux conditions initiales différentes lorsque une résistance
-
- Commenter et interpréter précisément les allures des tensions
et dans les 2 cas et en faisant le lien avec les questions précédentes.
Quelle propriété possède le circuit vis-à-vis de ses conditions initiales?
On souhaite que le comportement du circuit de la figure 9 réalisé avec des ALI réels soit le plus proche possible de celui décrit par l'équation différentielle établie à la questionsur une durée de l'ordre de la centaine de secondes. En choisissant , et deux résistances , de valeur identique on obtient finalement les résultats expérimentaux présentés sur la figure 12 .
- Commenter et interpréter précisément les allures des tensions
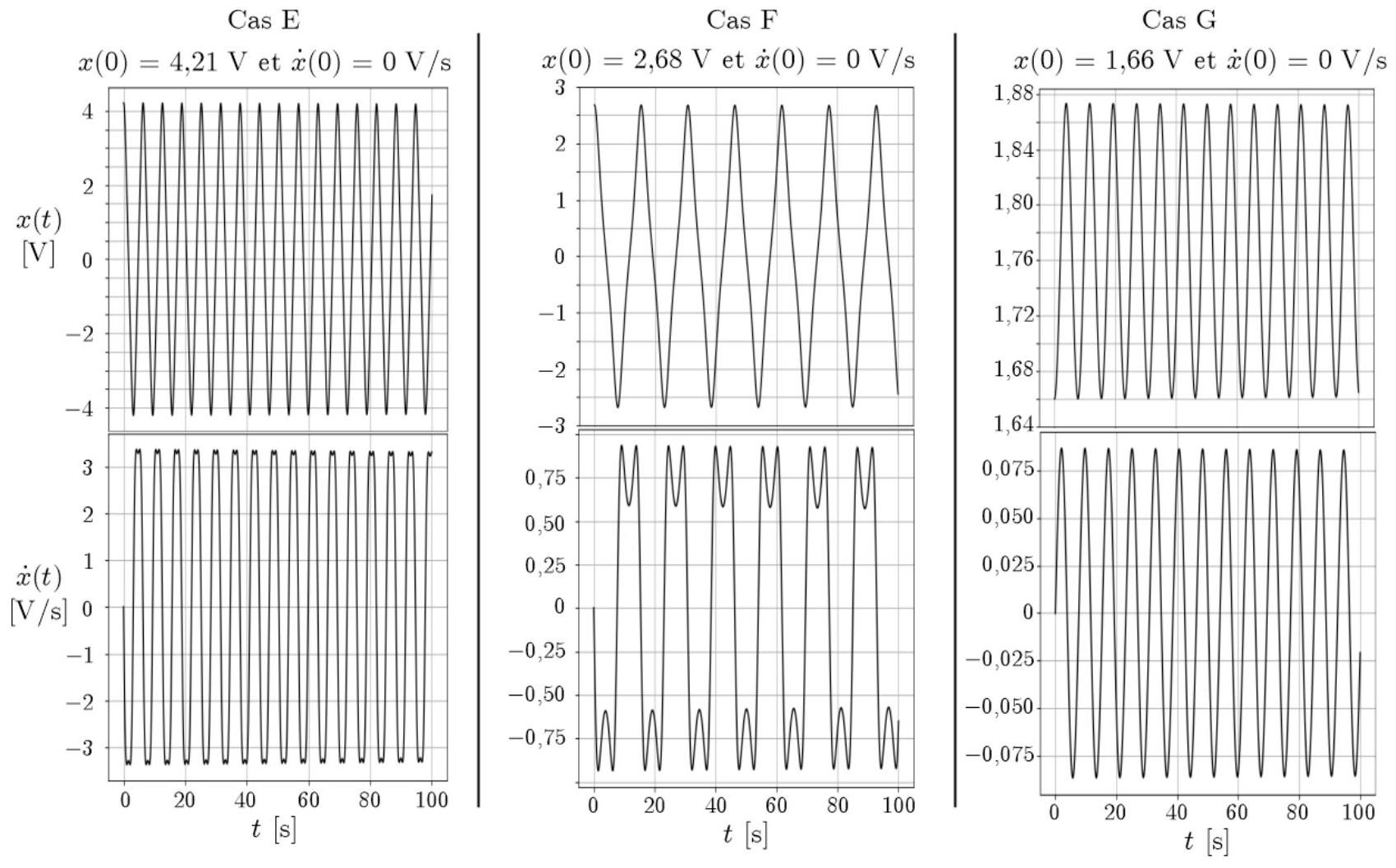
Figure 12 - Relevés expérimentaux pour trois conditions initiales différentes lorsque les paramètres du circuit de la figure 9 sont correctement réglés avec une résistance
-
- En appuyant votre raisonnement sur une équation différentielle que l'on essaiera de rapprocher le plus possible de celle de Duffing obtenue à la question 28, comparer qualitativement les valeurs de
(cas C et D de la figure 11) et de (cas et G de la figure 12).
- En appuyant votre raisonnement sur une équation différentielle que l'on essaiera de rapprocher le plus possible de celle de Duffing obtenue à la question 28, comparer qualitativement les valeurs de
Apparait-il d'autres conditions que les composants du circuit de la figure 9 devraient vérifier pour lui assurer le comportement souhaité? Les préciser.
