J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Physique 2 PC 2018

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2018
Filière
PC
Matière
Physique
Mines PCMines 2018PC PhysiquePhysique 2018
2025_09_04_619f7dda9a9e830d90bdg

A2018 - PHYSIQUE II PC

CONCOURS MINES COMMUN PONTS

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH, MINES SAINT-ÉTIENNE, MINES NANCY, IMT Atlantique, ENSAE PARISTECH.
Concours Centrale-Supélec (Cycle International), Concours Mines-Télécom, Concours Commun TPE/EIVP.

CONCOURS 2018

DEUXIÈME ÉPREUVE DE PHYSIQUE

Durée de l'épreuve : 4 heures

L'usage de la calculatrice et de tout dispositif électronique est interdit.
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :

PHYSIQUE II - PC

L'énoncé de cette épreuve comporte 6 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

Electrons et atomes par l'expérience

Ce problème présente un certain nombre de modèles et d'expériences mettant en jeu des électrons et des atomes. Les vecteurs sont repérés par le fait qu'ils sont surmontés d'une flèche dans le cas général ( ) ou d'un chapeau lorsqu'ils sont unitaires ( ). Un point sur une fonction du temps désigne sa dérivée temporelle : . Les applications numériques seront des ordres de grandeurs avec au plus deux chiffres significatifs, les données nécessaires à celles-ci sont rassemblées à la fin du sujet.

I. - Modèle classique de Thomson de l'atome

On modélise le mouvement de l'électron (masse , charge ) d'un atome d'hydrogène par celui d'un oscillateur harmonique effectuant de petites oscillations autour d'une position d'équilibre stable. Le centre du noyau étant fixe en , l'électron oscille selon un axe ( ), il est répéré par le vecteur ou désigne sa distance à l'origine . Il subit une force de rappel de la part du noyau : avec .
On montre que toute charge accélérée rayonne un champ électromagnétique. L'électron oscillant, il émet donc un rayonnement dont la puissance moyenne (sur une période d'oscillation de l'électron) est donnée par la formule de Larmor
Afin de justifier le caractère harmonique de la force de rappel subie par l'électron de la part du noyau, on adopte le modèle de Thomson. On modélise le noyau d'un atome d'hydrogène par une boule de centre et de rayon au sein de laquelle évolue l'électron, ce dernier restant à l'intérieur du noyau. La charge totale du noyau est uniformément répartie dans son volume.
  • 1 - En utilisant le théorème de Gauss en coordonnées sphériques, déterminer le champ électrique dû au noyau au sein de celui-ci (i.e. pour ). En déduire la force qu'exerce le noyau sur l'électron lorsque celui-ci se déplace uniquement suivant ( ). Faire le lien avec la force de rappel donnée précédemment en identifiant en fonction de et .
  • 2 - Déterminer, dans le cas d'oscillations libres, en fonction des caractéristiques du système (on choisira comme conditions initiales et ) et en déduire l'expression de l'énergie mécanique de l'électron en fonction de et .
  • - On considère dans la suite que cette énergie mécanique, malgré sa diminution due au rayonnement, diffère peu sur une période de celle que l'on vient d'établir en négligeant les pertes d'énergie. En tenant compte de la puissance moyenne perdue par rayonnement donner l'équation différentielle vérifiée par et montrer que dépend en fait du temps et se met sous la forme . Calculer la valeur de dans le cas de la raie bleue du spectre de l'atome d'hydrogène pour laquelle . Justifier a posteriori le calcul effectué.

FIN DE LA PARTIE I

II. - Émission et absorption de rayonnement

On reste dans le cadre du modèle de l'électron élastiquement lié au noyau de l'atome et l'on se place comme dans la première partie dans le cas particulier où l'électron repéré par le vecteur est en mouvement unidirectionnel suivant un axe ( ). Outre la force de rappel qu'il subit de la part du noyau, on modélise l'influence des pertes d'énergie mécanique de l'électron par une force de frottement fluide pour laquelle on prendra . On considère toujours les mêmes conditions initiales suivantes et .
  • 4 - Après avoir écrit le principe fondamental de la dynamique appliqué à l'électron, déterminer l'expression de . Simplifier cette expression (DL à l'ordre 1) compte tenu de la valeur très petite de devant 1 .
    - Donner, en fonction de et de , le temps caractéristique de décroissance des oscillations de et la pulsation des pseudo-oscillations que l'on mettra sous la forme : .
  • 6 - L'atténuation par rayonnement provoque une décroissance de l'énergie de l'oscillateur, comme cela a été vu à la question 3. Le rayonnement émis se présente comme un train d'ondes de longueur caractéristique . Donner en fonction de la vitesse de la lumière dans le vide et de . La lumière émise par l'électron freiné est-elle monochromatique?
  • 7 - Si la seule source d'élargissement de la raie spectrale était celle invoquée précédemment, quel commentaire pourrait-on faire sur la cohérence temporelle de cette source et sur la faisabilité d'une expérience d'interférence par exemple avec un interféromètre de Michelson?
  • 8 - On peut montrer, grâce à l'analyse de Fourier, que l'énergie rayonnée par l'électron par unité de fréquence est :
Représenter qualitativement la distribution spectrale de cette raie et déterminer sa largeur à mi-hauteur . En déduire la largeur de la raie en longueur d'onde et effectuer l'application numérique avec les valeurs de et données précédement. Exprimer en fonction de et . Dans ce modèle classique, quel commentaire peut-on effectuer sur le décalage en fréquence par rapport à la largeur naturelle de la raie ?
- L'élargissement d'une raie spectrale dû à l'effet Doppler est où est la vitesse moyenne d'agitation thermique des atomes qui émettent. Expliquer en quelques lignes, sans aucun calcul, en quoi consiste l'effet Doppler. On considère un gaz de masse molaire préalablement excité émettant de la lumière. Déterminer l'ordre de grandeur de pour un tel gaz se trouvant à la température . Calculer numériquement pour ce gaz ainsi que la longueur du train d'onde associée. Commenter ce résultat. À quelle température faudrait-il le refroidir pour pouvoir espérer mesurer la largeur naturelle de sa raie d'émission? Commenter ce résultat.

FIN DE LA PARTIE II

III. - Expérience de Faget et Fert

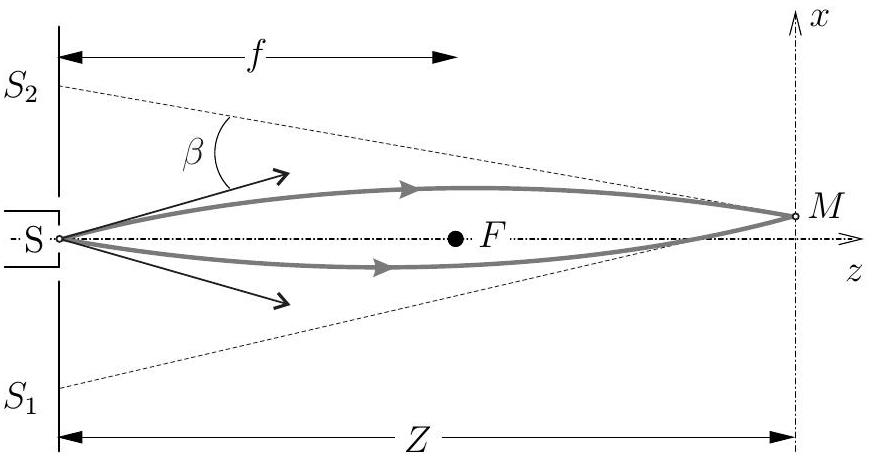
L'expérience réalisée à Toulouse en 1956 par Jean Faget et Charles Fert consiste à interposer un fil d'araignée métallisé (de rayon ) chargé positivement sur le trajet d'un faisceau d'électrons issus du même point , sortie d'un canon à électrons. Un électron est reçu en un point de l'écran. Lors de sa traversée de la cavité, attiré par le fil, l'électron a pu passer soit à droite, soit à gauche de ce dernier (voir figure 1).
Figure 1 - Expérience de Faget et Fert
Si les électrons passent à une faible distance du fil, on montre que l'angle de déviation des électrons est faible et pratiquement le même pour tous.
Dans ces conditions, tout se passe comme si les électrons, collectés sur l'écran après déviation, étaient émis suivant des trajectoires rectilignes en provenance des sources fictives et , telles que , avec et
Dans cette relation représente l'intensité du champ électrique à la surface du fil, la vitesse d'un électron et la charge élémentaire.
  • 10 - Décrire qualitativement ce qu'on observe sur l'écran.
  • 11 - Exprimer, en fonction de et de la distance au fil, le champ électrique créé par le fil chargé. En déduire le potentiel duquel dérive .
  • 12 - Sachant que l'on a et , calculer la différence de potentiel à imposer entre la sortie du canon et le fil pour avoir radian.
    13-Dans les expériences d'optique électronique les électrons arrivent un par un; décrire comment se forme la figure sur l'écran.
  • 14 - Comment interpréter l'onde associée aux électrons? Calculer l'interfrange de l'expérience dans le cas où . Comment varie-t-elle quand on augmente ?
    15-Que peut-on dire de la zone occupée par les franges (champ d'interférences) lorsqu'on augmente le potentiel .
  • 16 - Que pensez-vous de l'approche classique, au sens non-relativiste, effectuée ici?

FIN DE LA PARTIE III

IV. - Déviation du césium par un faisceau lumineux

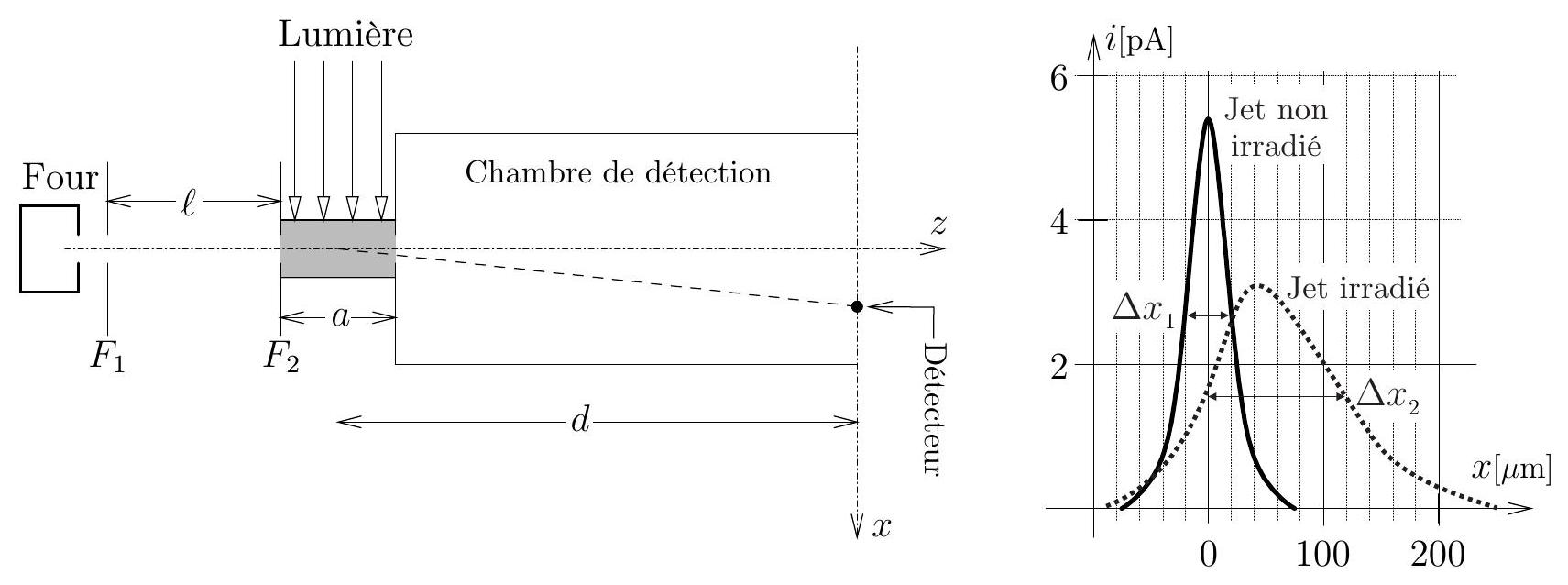
Afin de vérifier certains résultats de la théorie cinétique des gaz, on chauffe des atomes de césium placés dans un four percé d'un petit orifice. Ils en sortent avec une vitesse caractéristique . Deux fentes et parallèles à , de largeur et distantes de , permettent d'obtenir des trajectoires quasi parallèles à ( ) jusqu'au détecteur d'atomes : un fil chaud de de diamètre au sein duquel un courant d'ionisation est créé par le bombardement atomique. Ce courant est ensuite mesuré par un électromètre qui permet donc de déduire le nombre d'atomes reçus en fonction de la position du fil chaud.
Figure 2 - L'expérience de Picqué et Vialle (à gauche) et les résultats expérimentaux (à droite)
À travers un hublot, on irradie, sur une longueur , le jet atomique avec une lampe spectrale classique dont la longueur d'onde correspond à une raie d'absorption du césium. On considèrera que l'irradiation a lieu à une distance du détecteur. L'expérience a été réalisée par Jean-Louis Picqué et Jean-Louis Vialle au laboratoire Aimé Cotton de l'Univerité d'Orsay en 1972. Le dispositif est représenté sur la partie gauche de la figure 2
  • 17 - Rappeler l'expression de la quantité de mouvement d'un photon du faisceau irradiant.
    - On suppose que la quantité de mouvement totale se conserve lors de l'absorption d'un photon par un atome de césium, et l'on note l'angle que fait par rapport à ( ) la vitesse d'un atome de césium après cette absorption. Exprimer en fonction de et . En déduire la déviation d'un atome, au niveau du détecteur, associée à l'absorption d'un seul photon.
19-En analysant les résultats expérimentaux, estimer le nombre moyen de photons absorbés par les atomes lors de leur irradiation.
- Proposer une explication quantitative pour la largeur du pic non irradié. Proposer des explications qualitatives précises pour la largeur du pic irradié.

FIN DE LA PARTIE IV

V. - Mesures expérimentales de la durée de vie de certains états excités de l'hélium

On modifie l'expérience précédente, le but étant cette fois non pas de dévier le faisceau atomique mais d'exciter les atomes du jet afin de mesurer la durée de vie de l'état excité obtenu. Pour cela on travaille cette fois avec une vapeur d'hélium chauffée dans un four percé d'un petit orifice permettant aux atomes de s'échapper.
Le jet atomique ainsi obtenu est bombardé par un faisceau d'électrons énergétiques afin d'ioniser les atomes du faisceau. Les ions positifs ainsi formés sont ensuite accélérés entre les deux plaques percées d'un condensateur plan maintenu sous une différence de potentiel . Les cations sont ensuite à nouveau irradiés par un faisceau d'électrons, de faible énergie cette fois, qui les neutralise en les laissant dans un état excité correspond à l'état fondamental), juste avant leur sortie du condensateur.
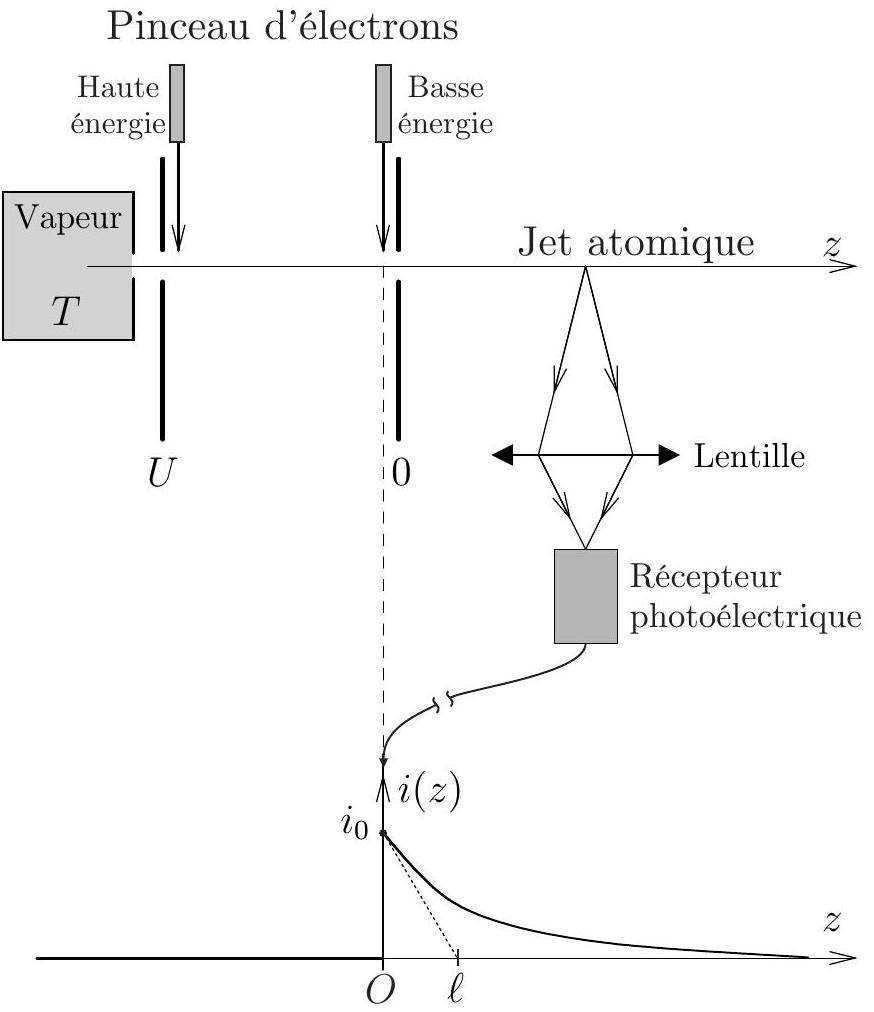
Figure 3 - Dispositif expérimental
Un atome excité à , a la probabilité d'être encore excité à l'instant . Pour mesurer la durée de vie de cet état excité, on dispose le long du jet atomique, une lentille et un récepteur photoélectrique qui peuvent se déplacer parallèlement à l'axe ( ) du jet. Il est ainsi possible d'isoler la lumière émise par une petite fraction du jet atomique situé à la distance de la zone irradiée (entre et ) et de tracer la courbe de variation de l'intensité différentielle reçue par le détecteur.
  • 21 - Dans ces expériences utilisant des jets atomiques, il est nécessaire de réaliser un vide poussé dans l'enceinte traversée par le jet atomique. Expliquer pourquoi.
  • 22 - Pourquoi est-il nécessaire d'ioniser au préalable les atomes d'hélium?
    - Quelle est la longueur d'onde de la lumière émise par le jet?
  • 24 - En négligeant la vitesse des atomes à la sortie du four devant celle-ci, calculer la vitesse des cations à la sortie du condensateur.
    - Déterminer la probabilité qu'un atome du jet se désexcite entre les instants et . En déduire la probabilité qu'un atome du jet se désexcite entre les cotes et .
    - On note la proportion du rayonnement émis dans la direction du détecteur et collecté par la lentille, la densité volumique d'atomes dans le jet et la section du jet. Déterminer l'expression de l'intensité lumineuse reçue par le détecteur.
  • 27 - La tangente à à l'origine, coupe l'axe des abscisses en . Calculer la durée de vie de l'état excité de l'atome d'hélium.

FIN DE LA PARTIE V

VI. - Irradiation d'une vapeur d'hydrogène atomique

Lorsque l'on porte de l'hydrogène à de très hautes températures, supérieures au millier de kelvins, on peut considérer que seuls les deux premiers niveaux d'énergie accessibles aux électrons, et , sont peuplés. On rappelle que la population du niveau d'énergie est donnée par la relation de Boltzmann où est une constante et la constante de Boltzmann.
On expose ce gaz à un rayonnement électromagnétique dont la fréquence est telle que les photons qui le constitue possèdent une énergie très supérieure à l'énergie d'ionisation de l'hydrogène . On peut donc faire l'hypothèse que cette irradiation ionise les atomes d'hydrogène (de masse ).
On analyse la distribution en vitesse des électrons (de masse ) ainsi émis. On observe que la distribution expérimentale de ces vitesses présente deux pics à des vitesses et dont les largeurs sont d'autant plus importantes que la température du gaz est élevée.
- Proposer une explication physique pour ce constat expérimental.
29- Rappeler l'expression en fonction de et d'un entier . Déterminer l'expression de et en fonction de et .
- Les conditions de cette expérience peuvent être comparées à celle de la surface de certaines étoiles. Une analyse spectroscopique permet de mesurer pour une étoile. Déterminer la température de sa surface en utilisant ce modèle. Cela vous semble-t-il réaliste? On étaiera sa réponse par des arguments quantitatifs.
  • 31 - Déterminer l'expression de la constante en fonction notamment du nombre total d'atomes contenus dans l'échantillon étudié.
  • 32 - On considère maintenant tous les niveaux d'énergie potentiellement excités de l'atome d'hydrogène. Quel est le nombre maximal d'électrons pouvant occuper le niveau d'énergie . Ce nombre est appelé dégénérescence de l'état . En déduire une expression de la constante sous la forme d'une série infinie. Que constatez-vous?
  • 33 - On rappelle que le -ième rayon moyen de l'orbite de BOHR d'un électron de l'atome d'hydrogène est donné par la relation
Proposer une explication permettant de résoudre le problème rencontré à la question précédente.

FIN DE LA PARTIE VI

Données numériques

Nombre d'Avogadro :
Constante de Planck :
Constante de Boltzmann :
Charge élémentaire :
Masse molaire de l'hydrogène :
Masse molaire de l'hélium :
Masse molaire du césium :
Masse de l'électron :
Masse d'un proton :
Vitesse de la lumière dans le vide:
Électron-volt :
Permitivité diélectrique du vide :

FIN DE L'ÉPREUVE

Mines Physique 2 PC 2018 - Version Web LaTeX | WikiPrépa | WikiPrépa