Version interactive avec LaTeX compilé
A 2001 PHYS. PC II
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE, ÉCOLE POLYTECHNIQUE (FILIÈRE TSI)
CONCOURS D'ADMISSION 2001
SECONDE ÉPREUVE DE PHYSIQUE
Filière PC
(Durée de l'épreuve :
Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPE-EIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE II -Filière PC
Cet énoncé comporte 4 pages de texte
Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPE-EIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE II -Filière PC
Cet énoncé comporte 4 pages de texte
Abstract
- Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu’il est amené à prendre. - Tout résultat fourni dans l'énoncé peut être utilisé, même s’il n’a pas été démontré. - Il ne faudra pas hésiter à formuler tout commentaire qui vous semblera pertinent, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.
Conventions typographiques : un vecteur est noté en gras (A), sa norme en italique
ULTRACENTRIFUGATION
On appelle ultracentrifugation la centrifugation effectuée au moyen d'appareils tournant à vitesse très élevée, par exemple supérieure à 20000 tours par minute. Inventée et mise au point principalement par SVEDBERG (Prix Nobel de chimie 1926) au début des années 1920, cette technique s’est progressivement répandue dans la plupart des laboratoires de biologie moléculaire. C’est une des principales méthodes de séparation des macromolécules biologiques (protéines, acides nucléiques) et de mesure des masses moléculaires. Ce problème aborde les principes de cette technique.
Une ultracentrifugeuse est schématisée sur la fig. 1. Le rotor (partie mobile) est percé de cavités cylindriques en nombre pair, régulièrement disposées autour de l'axe du rotor. Chaque cavité peut recevoir une cellule constituée d'un cylindre de métal percé d'une cavité en forme de secteur.
Première partie : ultracentrifugation dynamique (sédimentation)
1. Définition du coefficient de sédimentation
On place dans les cellules du rotor une solution composée d'un solvant de masse volumique
leur volume massique
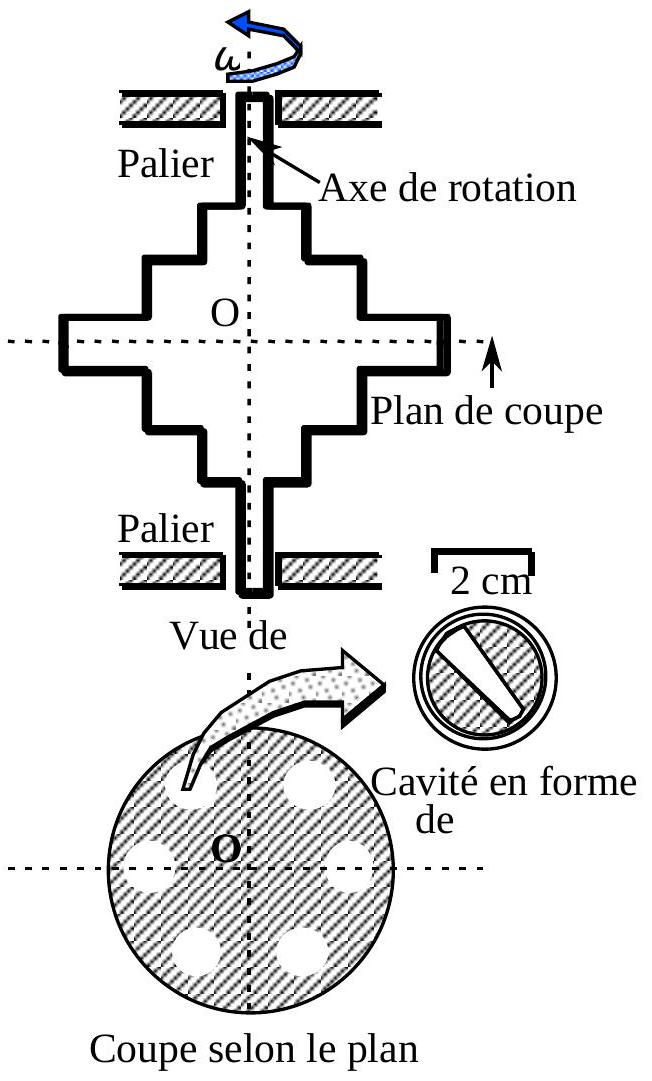
Fig. 1 : schéma de principe du rotor d'une ultracentrifugeuse
- 3 - On considère donc uniquement la partie radiale, selon
, du mouvement relatif de la particule par rapport au solvant. Donner alors, sans la démontrer, l'expression du gradient de pression dans le référentiel lié au solvant en un point situé à la distance de l'axe du rotor. En déduire l'expression de la résultante des forces de pression («poussée d'Archimède») s’exerçant sur une particule de soluté, en fonction de et .
- Faire le bilan des forces agissant sur la particule de soluté précédente et montrer que cette dernière acquiert pratiquement la vitesse limite , avec .
L'approximation faite dans (2) est-elle justifiée a posteriori ? On peut ainsi affecter aux particules de soluté la «masse apparente»。
- Montrer que la dimension du coefficient est celle d'un temps. L'unité pour est le svedberg, noté S : seconde. - 6 - Estimer l'ordre de grandeur du temps au bout duquel la vitesse limite est pratiquement atteinte.
2. Équation de sédimentation (LAMM, 1929)
On note
3. Solution de l'équation de sédimentation en l'absence de diffusion
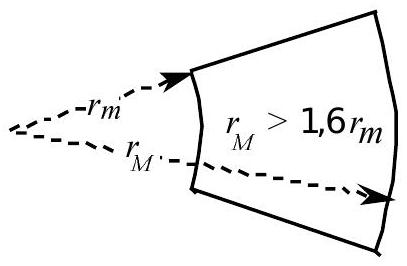
Fig. 2: cellule
On note
Exprimer le temps caractéristique
4. Relation d'EINSTEIN (1905)
On s'intéresse maintenant au régime stationnaire de l'équation de sédimentation, correspondant à la limite
13 - Pourquoi la diffusion ne peut-elle plus maintenant être négligée ?
Seconde partie : ultracentrifugation d'équilibre
On ultracentrifuge à 50000 tours par minute une solution aqueuse concentrée de chlorure de césium ( CsCl ). On admet que la solution reste électriquement neutre localement en tout point de la cellule d'ultracentrifugation. On adopte l'hypothèse simplificatrice que les ions
1. On suppose d'abord qu'il n'y a pas d'autre soluté dissous que le chlorure de césium.
2. On ajoute à la solution de chlorure de césium ainsi préparée une petite quantité de soluté (macromolécules) à analyser.
On note
21 - Donner la condition permettant de séparer par ultracentrifugation des substituants isotopiques de même volume massique mais de masses molaires différentes. Donner aussi la condition permettant de séparer par ultracentrifugation deux macromolécules isomères, de masses molaires égales mais de volumes massiques différents (puisque leur structure développée est différente).
FIN DU PROBLÈME
FIN DE L'ÉPREUVE
