J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Physique 2 MP 2009

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2009
Filière
MP
Matière
Physique
Mines MPMines 2009MP PhysiquePhysique 2009
2025_09_04_a72dc743c7cd705928f6g

ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES. ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE, ÉCOLE POLYTECHNIQUE (FILIÈRE TSI)

CONCOURS D'ADMISSION 2009
SECONDE ÉPREUVE DE PHYSIQUE
Filière MP

(Durée de l'épreuve: heures)L'usage de la calculatrice est autorisé

Sujet mis à disposition des concours : ENSAE (Statistique), ENSTIM, INT, TPE-EIVP, Cycle international

Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE II — MP.
L'énoncé de cette épreuve comporte 7 pages.
  • Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il est invité à le signaler sur sa copie et à poursuivre sa composition en expliquant les raisons des initiatives qu'il aura été amené à prendre.
  • Il ne faudra pas hésiter à formuler les commentaires (incluant des considérations numériques) qui vous sembleront pertinents, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.

OSCILLATIONS DE PUISSANCE À HAUTE FRÉQUENCE

L'énoncé de cette épreuve comporte deux parties complètement indépendantes. Les vecteurs sont représentés en caractères gras : . Un système d'axes orthonormés direct est associé à la base cartésienne ( ). Pour toute grandeur , on note .
Historiquement, les tubes à vide et à faisceaux d'électrons (qui ont donné son nom à l'électronique) ont progressivement été remplacés par des composants à semi-conducteurs (diodes, transistors, etc.). Toutefois, les tubes à circulation d'électrons dans le vide (klystron, magnétron) restent d'un emploi courant dans le domaine des hautes fréquences et des fortes puissances. Ce problème décrit ces deux dispositifs toujours largement utilisés.

I. - Le magnétron, oscillateur hyperfréquences

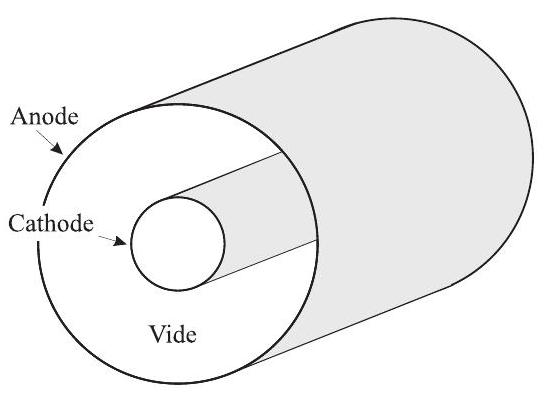
Fig. 1 - Le magnétron (vue d'ensemble)
Un magnétron (système équipant tous les fours à micro-ondes) est constitué d'un tube à vide et de deux électrodes, cylindriques et coaxiales. Un champ électrique intense règne dans l'espace inter-électrodes, et les électrons, émis par la cathode centrale, se dirigeraient vers l'anode externe à grande vitesse si le champ magnétique était absent (fig. 1). On impose un champ magnétique stationnaire qui, courbant les trajectoires électroniques, les amène à rester contenues dans l'espace inter-électrodes.
Les électrons acquièrent alors des trajectoires rapidement tournantes et leur passage devant des cavités résonantes provoque l'apparition, dans celles-ci, de champs électromagnétiques rapidement variables. Dans les fours à micro-ondes à usage domestique, la fréquence d'émission est normalisée à . Le rayonnement micro-onde est alors conduit vers la zone à chauffer par un guide d'ondes. Le magnétron a été inventé par le physicien américain Albert Hull en 1921 et perfectionné par le physicien japonais Kinjiro Okabe en 1928. Il a été mis en application dès la seconde guerre mondiale comme source d'ondes de haute fréquence pour les systèmes radar en Grande-Bretagne. Ce qui suit n'est pas une description complète du magnétron, mais seulement une mise en équations de certains mouvements possibles des électrons dans le magnétron. En cas de besoin on rappelle l'expression des opérateurs divergence et gradient dans le système de coordonnées associé à la base cylindrique représentée sur la figure 2
Pour tout champ de vecteur
Pour tout champ scalaire
Dans tout ce problème on négligera le poids des électrons.

I.A. - Le magnétron sans champ magnétique

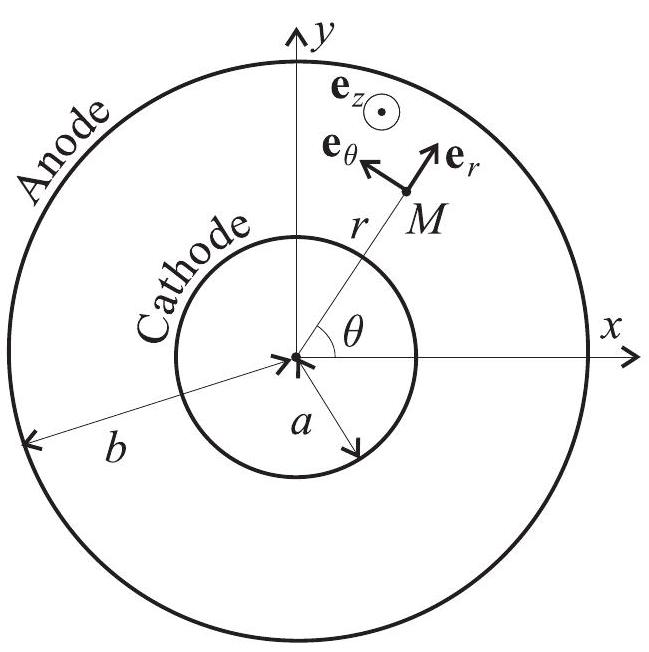
FIG. 2 - Le magnétron (vue de face)
Le schéma de la figure 2 représente la cavité, vide, comprise entre l'électrode interne (cathode), cylindrique de rayon , portée au potentiel nul, et la cavité externe, cylindrique de rayon , portée au potentiel constant . On considère un point , de coordonnées cylindriques ( ) dans la base , représenté sur la figure 2 .
-1-En négligeant tout effet de bord, déterminer le potentiel électrostatique en situé dans l'espace interélectrodes, supposé vide.
  • 2 - Des électrons sont émis au niveau de la cathode par effet thermoélectronique à vitesse initiale négligeable. Quelle est leur trajectoire? Exprimer pour un électron situé en en fonction de , de sa charge , de sa masse et des quantités et .
    - Exprimer la durée du trajet de la cathode à l'anode. On posera .

I.B. - Le magnétron vide, avec un champ magnétique.

On considère toujours que l'espace inter-électrodes est vide, soumis à la même répartition de potentiel électrostatique que celle décrite à la question 1 ; on lui superpose le champ magnétostatique , uniforme et stationnaire, orthogonal au plan de la figure 2.
  • 4-Montrer que la trajectoire d'un électron, émis au niveau de la cathode sans vitesse initiale, est plane. On pourra décrire ce mouvement en coordonnées polaires ( ), en projection sur la base polaire . Montrer que l'énergie mécanique de cet électron est conservée. En déduire une constante du mouvement sous la forme d'une relation entre et .
  • 5 - En écrivant le théorème du moment cinétique pour le mouvement de l'électron, déduire l'existence d'une autre constante du mouvement faisant apparaître .
    - On appelle champ de coupure la valeur minimale du champ magnétique que l'on doit imposer pour qu'aucun électron ne puisse atteindre l'anode. Exprimer en fonction de et . Donner l'expression approchée de si ; cette relation porte le nom d'équation de Hull. On note la valeur prise par la vitesse angulaire au moment où l'électron est le plus éloigné de la cathode, à la distance de l'axe du magnétron, et la valeur particulière de si . Exprimer en fonction de et .

I.C. - Le magnétron, avec charge d'espace et champ magnétique.

On étudie un mode particulier de fonctionnement du magnétron (mode de Brillouin) dans lequel tous les électrons qui ne sont pas dans le voisinage immédiat de la cathode ont un mouvement circulaire d'axe à la même vitesse angulaire . Les potentiels des électrodes de rayon et sont inchangés, le champ magnétique est toujours constant et selon .
- Montrer que le mode de Brillouin n'est pas compatible avec le potentiel électrostatique issu de l'hypothèse d'un espace interélectrode vide. Expliquer pourquoi la prise en compte d'une charge dans l'espace interélectrode peut éventuellement permettre d'obtenir un mode de Brillouin.
- Déterminer l'expression du potentiel entre les électrodes qui permet d'obtenir le mode de Brillouin idéal, c'est-à-dire celui pour lequel tous les électrons sont en mouvement circulaire à vitesse angulaire constante. On exprimera en fonction de et et on constatera que ce mode ne peut être obtenu que pour une valeur particulière du champ magnétostatique que l'on déterminera en fonction de et .
- On considère toujours que les électrons sont émis à vitesse nulle à la cathode. Montrer que pour un mode de Brillouin idéal, seuls les électrons situés loin de la cathode ( ) possèdent approximativement l'énergie mécanique qu'ils avaient au moment de leur émission. Exprimer pour ces électrons périphériques et en fonction de et .
— On donne et . Comment choisir pour obtenir des oscillations périphériques de fréquence ? Quelle doit être la valeur de ?

FIN DE LA PARTIE I

II. - Le klystron, amplificateur hyperfréquence

Cette partie décrit le principe de fonctionnement du klystron à deux cavités, dispositif amplificateur de tension hyperfréquences inventé en 1937 par William Hansen, Russell et Sigurd Varian. Le fonctionnement du klystron à deux cavités est fondé sur la modulation de vitesse d'un faisceau d'électrons. Ses inventeurs décrivaient le principe du klystron au moyen de l'analogie suivante : «imaginez un flot continu de véhicules circulant de San Francisco à Palo Alto ; si les voitures quittent San Francisco à intervalles réguliers et avec la même vitesse, alors, jusqu'à leur arrivée à Palo Alto, elles seront régulièrement espacées et on observera un flux uniforme de véhicules. Mais supposez que, d'une manière quelconque, la vitesse de certaines voitures puisse être légèrement augmentée à leur départ de San Francisco, tandis que d'autres seraient légèrement ralenties. Alors, au fur et à mesure de leur trajet, les voitures rapides rattraperaient les plus lentes et elles formeraient des paquets. Ainsi, si la vitesse des voitures est assez différenciée et la durée du trajet suffisante, le flux uniforme serait transformé. Dans le cas idéal, l'arrivée à Palo Alto se produirait en groupes clairement définis ». De la même façon, dans un tube à électrons, le contrôle du flux d'électrons peut suivre le même principe de «formation de paquets » par modulation de la vitesse plutôt que par un contrôle direct du flux par une électrode de sortie.
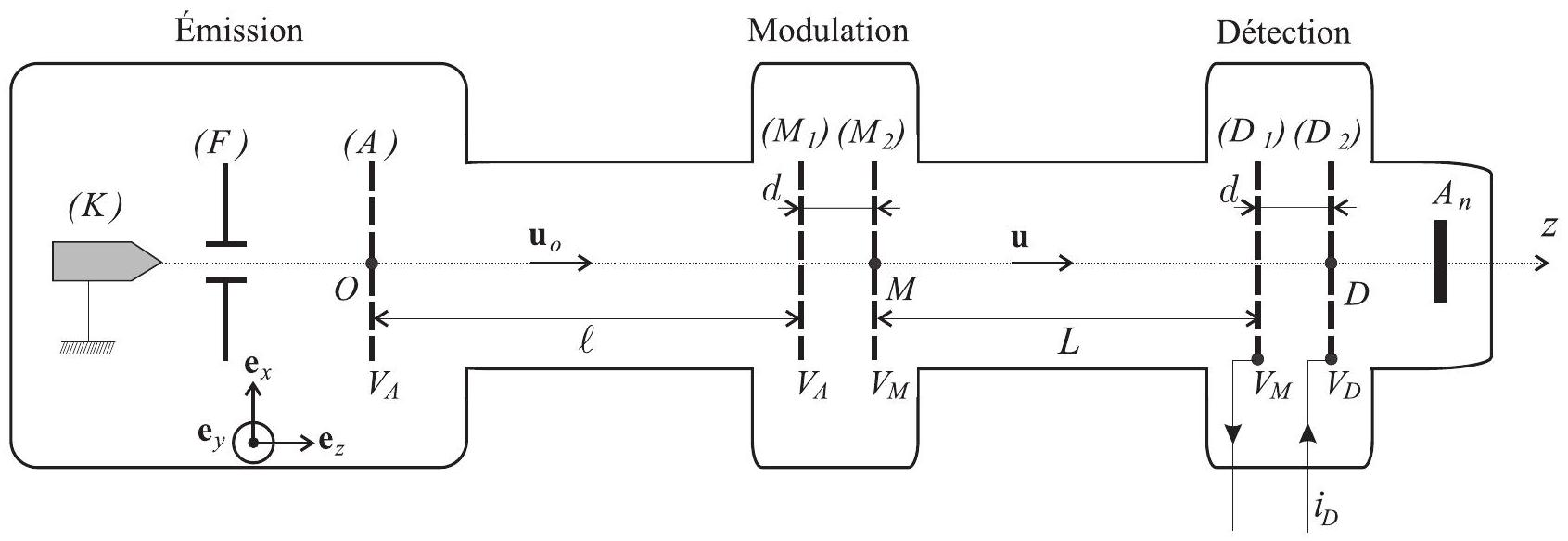
Le klystron est un tube à électrons (particules de masse et de charge supposées non relativistes dans tout le problème) utilisé en modulation de vitesse, décrit sur la figure 3 . Les électrons sont émis dans le vide qui règne dans la cavité par effet thermoélectronique dans un canon à électrons formé
Fig. 3 - Principe du klystron à deux cavités
d'une cathode chauffée ( ), portée au potentiel , d'une grille de focalisation ( ) et d'une grille d'accélération ( ) portée au potentiel constant . La sortie des électrons de la cathode chauffée se fait à l'abscisse , à vitesse initiale négligeable.
Après la traversée de la grille d'accélération, positionnée à l'abscisse , les électrons forment un faisceau homocinétique, de vitesse , colinéaire à l'axe du klystron. Ils atteignent deux grilles dites de modulation, ( ) et ( ) séparées par la distance et respectivement portées aux potentiels et . La fréquence est imposée par un oscillateur non décrit ici. On désigne par la distance et l'on suppose que (voir figure 3).
À la sortie de la zone de modulation, les électrons de vitesse traversent un espace de glissement de longueur avant d'atteindre les grilles de détection, ( ) et ( ) séparées par la distance et respectivement portées aux potentiels et ; on suppose que (voir figure 3). Enfin, une anode collecte les électrons qui ont traversé le système sans être interceptés.
Dans tout le problème, on notera le courant électrique qui circule, à l'instant et à la cote , dans une section droite du tube orientée dans le sens des décroissants de sorte que soit positif. On néglige tout champ magnétique et l'on suppose que le potentiel électrique qui règne dans le tube n'est fonction que de et du temps ; pour cette raison, à partir de la question 13, le champ électrique dans le tube sera noté .

II.A. - Étude du faisceau d'électrons dans le tube

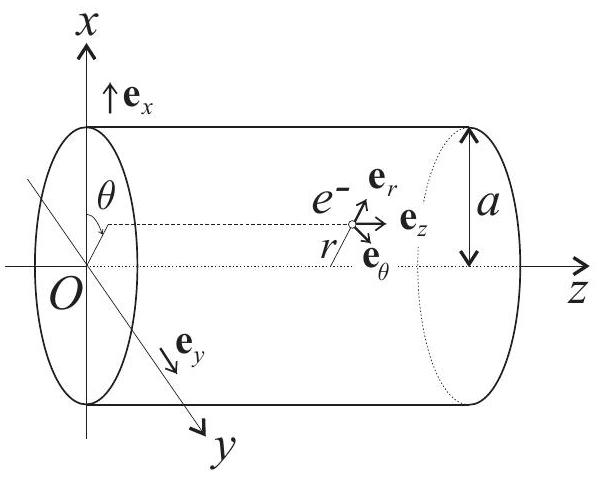
Dans la région , on notera le courant électrique qui traverse le tube; le faisceau électronique est supposé cylindrique, de rayon , de section . On pourra utiliser les coordonnées cylindriques ( ) exprimées dans la base cylindrique locale représentée sur la figure 4.
- Représenter sur un schéma le sens du courant . Exprimer en fonction de et de la charge volumique électronique , supposée uniformément répartie dans le cylindre. Montrer que le champ électrique créé par cette distribution cylindrique de charges ne dépend que de la distance radiale à l'axe du cylindre. En déduire l'expression de en fonction de , de la permittivité du vide ainsi
FIG. 4 - Coordonnées cylindriques
que de , et .
- On considère qu'un électron situé à la périphérie du faisceau évolue dans le champ uniforme . Calculer la déviation radiale qu'il subit en fonction de et de la durée du trajet d'un électron périphérique entre et . En déduire que l'on ne peut considérer que le faisceau d'électrons reste approximativement cylindrique qu'à une certaine condition, que l'on écrira sous la forme . On exprimera en fonction de et . On dira alors que l'on néglige la défocalisation du faisceau. On fera cette approximation dans toute la suite du problème.
- Exprimer, en fonction de et , l'équation différentielle qui régit les variations de en fonction de dans la région . En déduire le potentiel en fonction , et . À quelle condition (exprimée sous la forme ) peut-on considérer que est uniforme dans cette région ? On exprimera en fonction de et . Expliquer pourquoi cette approximation consiste à négliger la charge d'espace dans le tube. On fera cette approximation dans toute la suite du problème.
- Déterminer l'expression de pour et tracer la courbe correspondante.
- Déterminer la vitesse des électrons qui traversent la grille de modulation ( ) à l'instant , on l'exprimera en fonction de et de . Donner une expression approchée de lorsque ; on se placera dans ce cas dans toute la suite du problème.
  • 16 - Expliquer pourquoi le générateur qui alimente les grilles de modulation ne fournit, en moyenne aucune énergie. Quelles causes consommatrices de puissance, non prises en compte dans ce qui précède, pouvez-vous imaginer au niveau du dispositif de modulation ?

II.B. - Étude de la modulation de vitesse du faisceau d'électrons

- On considère ici des électrons qui sont passés par la grille de modulation ( ) à l'instant ; on pose . Ces électrons atteignent la grille de détection ( ) à l'instant ; on posera et . Quelles sont les dimensions physiques de et ? En se limitant au premier ordre en , exprimer en fonction de et .
- Sur un intervalle symétrique centré en 0 , tracer l'allure des courbes donnant en fonction de pour et . Expliquer pourquoi porte le nom de paramètre de groupement.
  • 19 - Dans cette question seulement, on considère que . L'étude précédente montre que l'on peut regrouper les électrons. Pour fixer les idées, considérons l'intervalle de temps centré sur 0 de telle manière que , tel que tous les électrons qui ont été émis de ( ) pendant une durée arrivent sur ( ) pratiquement au même instant , à près. Déterminer en fonction de et . À quelle fraction de la période du signal de modulation cette durée correspond-elle?
    Application numérique : on donne ainsi que . Déterminer et .
    - On considère que la durée du trajet d'un électron entre et est nulle. L'intensité du courant électrique qui atteint la grille de modulation ( ) à l'instant est donc . On note l'intensité du courant électrique qui atteint la grille de détection ( ) à l'instant . Relier et . En déduire que
- On note la phase de l'onde de courant qui se propage le long de l'axe du klystron, à l'instant où cette onde atteint la grille de détection ( ). Exprimer en fonction de et . Montrer que, si , le courant peut être considéré comme une fonction de . Quelle est la période de cette fonction ? Est-ce une fonction paire ou impaire de ?
22- On cherche la décomposition de Fourier de sous la forme :
Déterminer , puis pour tout . On donne l'expression intégrale de la fonction de Bessel de première espèce d'ordre :
Exprimer simplement en fonction de et de . On conservera cette expression dans la suite même si .

II.C. - Dimensions et accord du klystron

L'onde de courant parvenant au détecteur sera détectée sous la forme du courant alternatif ; celui-ci s'écrit, en se limitant au premier terme de la série de Fourier, proportionnellement à la fonction de Bessel :
où est le rendement de détection, et le courant strictement positif produit par le canon à électrons. Le tracé de est reporté sur la figure 5 . On notera que pour et ; le premier maximum de est atteint pour et vaut .
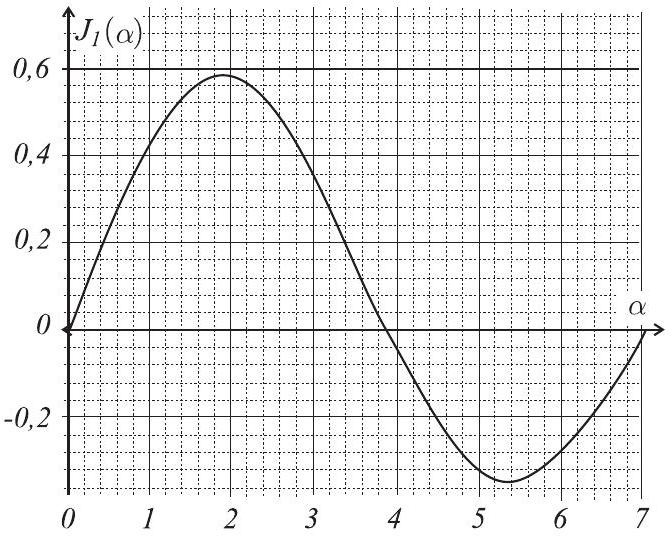
Fig. 5 - Fonction de Bessel
23 - À quelle distance de la grille de modulation , la grille de détection doit-elle être placée pour obtenir un courant détecté d'amplitude maximale ? On exprimera en fonction de la fréquence du signal de modulation, de et .
24 - On donne et . Calculer la fréquence pour laquelle est accordé le klystron. Dans quel domaine spectral cette fréquence se situe-t-elle?

II.D. — Étude du système de détection

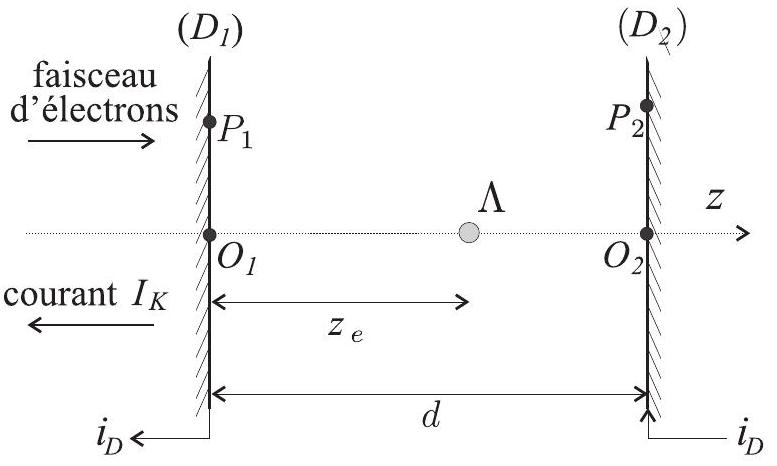
Le système des deux grilles de détection est ici assimilé à deux plans métalliques, parfaitement conducteurs, disposés à la distance l'un de l'autre. On note et les intersections des deux grilles de détection et avec l'axe . On considère qu'à un instant donné, un seul électron, noté , se trouve entre ces deux grilles; il a alors parcouru la distance telle que dans l'espace défini par les deux grilles (voir figure 6). Soit (respectivement ) un point quelconque de la grille ( ) (respectivement repéré par la distance (respectivement ).
FIG. 6 - Grilles de détection
Dans toute la partie II.D, on notera et les potentiels respectifs des grilles ( ) et ( ) dont les dimensions transverses sont supposées très supérieures à , de manière à négliger tout effet de bord. L'ensemble de l'étude électrique sera mené dans le cadre de l'électrostatique.
25-En l'absence de tout électron entre les grilles, déterminer les densités surfaciques de charge et portées par les grilles. On les exprimera en fonction de , de et de la permittivité du vide .
- En sa présence (voir fig. 6), on admet que la charge ponctuelle de l'électron influence totalement les deux plans métalliques, c'est-à-dire que toute ligne de champ issue d'un point du plan passe par le point de cote où se trouve l'électron. Tracer l'allure des lignes de champ du champ électrique dans l'espace compris entre ( ) et ( ). Tracer également l'allure des surfaces équipotentielles.
En présence de cet électron, on appelle et les charges surfaciques aux points et , et et les charges totales portées par les deux facades des grilles et en regard. Quels sont les signes de et ? Quels sont les signes de et ? Justifier. Que peut-on dire de ?
- Quelles sont les valeurs limites et des charges et à l'instant où l'électron vient de pénétrer dans l'espace de détection, c'est-à-dire lorsque ? Expliciter de même les valeurs limites et des charges et à l'instant où l'électron va quitter l'espace de détection c'est-à-dire lorsque . Finalement, quelle est la charge qui a circulé dans les grilles de détection lors du passage d'un électron à travers les grilles de détection?
On note le courant transporté par les électrons qui circulent le long de l'axe du klystron, et qui traverse les grilles de détection. Ce courant provoque la circulation d'un courant électrique variable dans le circuit refermé sur les grilles de détection.
- Que vaut si le courant est constant?
On suppose que le courant comporte maintenant une partie sinusoïdale qui se propage à la vitesse . On considère la charge électrique circulant entre les grilles sous l'effet du seul courant alternatif .
- Exprimer la charge comprise, à l'instant , entre les deux plaques, sous forme intégrale. Déterminer la variation . On supposera que la largeur est faible devant . En déduire le courant . Quel est, à la pulsation , le rendement du système de détection?

FIN DE LA PARTIE II

FIN DE L'ÉPREUVE

Mines Physique 2 MP 2009 - Version Web LaTeX | WikiPrépa | WikiPrépa