Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

Le canon, fournisseur d'impulsion

L'impulsion désigne, dans le langage général, l'élan initial qu'on donne à un objet (projectile) qui poursuit ensuite son mouvement. Il a un sens plus spécifique en physique, depuis son introduction sous le nom impetus au moyen-âge : ainsi, un point matériel de masse

et de vitesse

a pour impulsion

et un système étendu de masse

et de barycentre

a pour impulsion

. Cette grandeur joue par ailleurs un rôle essentiel en physique microscopique, quantique et relativiste.
L'acquisition d'impulsion pour un projectile est le but d'un canon. Le sujet comporte trois problèmes

(description hydrodynamique d'un canon à eau), II (étude thermodynamique d'un canon à poudre explosive) et III (modélisation électromagnétique d'un canon électromagnétique). Ils sont totalement indépendants. Dans l'énoncé des questions posées, exprimer signifie donner une expression littérale et calculer signifie donner une valeur numérique; toutes les applications numériques seront réalisées avec seulement deux chiffres significatifs; on notera que

I Canon à eau

Le canon à eau est un dispositif utilisé par les pompiers pour éteindre les incendies tout en restant à distance des flammes; on en utilise aussi dans les opérations de police anti-émeutes. Le but du dispositif est de projeter à grande distance, à travers un tube métallique cylindrique de diamètre

et de longueur

, de l'eau avec une vitesse initiale

élevée (voir figure 1 ). Un tel canon doit, dans le cas le plus favorable, avoir une portée maximale

. On supposera que l'eau est un liquide incompressible de masse volumique

et peu visqueux,

Figure 1 - Canon à eau (photo SDIS de la Haute-Loire et Jéremy Rousseau) et son schéma

Après être sorties du canon, les gouttes d'eau sont en mouvement sous la seule action du champ de pesanteur, d'intensité

1. En négligeant tout frottement, montrer que la trajectoire des gouttes est parabolique et que la portée maximale est atteinte lors d'un tir sous un angle de (figure 2).
  Exprimer en fonction de et puis calculer sa valeur.
  En déduire le diamètre du canon s'il permet d'assurer un débit sortant de (cas des plus gros canons à eau commercialisés).
1. Justifier que la totalité du jet est isobare à pression identique à celle bar de l'air. Peut-on appliquer le théorème de Bernoulli le long de cet écoulement parabolique?
  Quelle est en particulier la vitesse minimale de l'eau entre sa sortie du canon en et son impact au sol?

Figure 2 - Canon à eau en configuration de portée maximale

Si la pression de sortie du canon est bien pratiquement identique à

, sa pression à l'entrée du tube, c'est-à-dire juste à la sortie de la pompe qui l'alimente, est plus élevée; on la notera

. La chute de pression

le long du tube est due aux effets combinés de la viscosité de l'eau et de la rugosité relative du matériau formant l'intérieur du tuyau du canon; cette grandeur mesure le rapport

de la hauteur moyenne des aspérités au diamètre du tuyau. La hauteur

des aspérités à l'intérieur d'un tuyau de canon à eau sera comprise entre

; sa longueur est

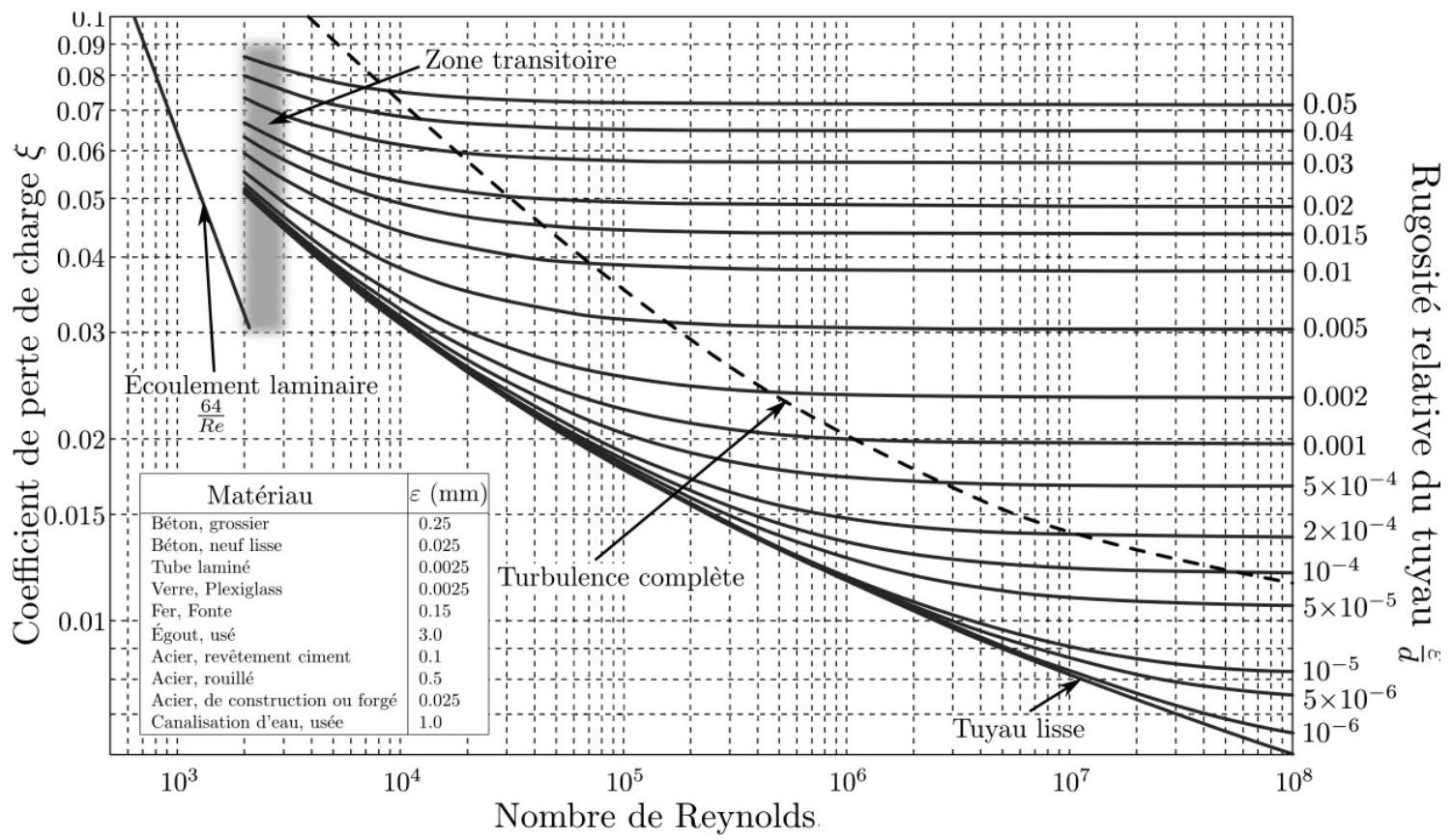
Figure 3 - Diagramme de Moody

Le diagramme de Moody (figure 3) permet alors de déterminer le facteur de friction

de Darcy-Weisbach ; on peut alors en déduire la perte de charge selon :

1. Rappeler l'expression du nombre de Reynolds d'un écoulement, puis calculer celui-ci pour l'eau à l'intérieur du canon à eau. Que peut-on en conclure?
  . Déterminer les valeurs extrêmes de puis de ; commenter.
  La pompe qui alimente un tel canon prélève l'eau dans un réservoir de grande dimension contenu dans le camion, à la même altitude que la pompe, au repos et à pression atmosphérique. Cette pompe accélère donc l'eau (qui atteint la vitesse à l'entrée du canon) et augmente sa pression pour compenser les pertes de charge de la loi de Darcy-Weisbach (1), elle atteint bar à l'entrée du canon, pour une sortie de celui-ci sous pression atmosphérique.
1. En négligeant tout frottement mécanique à l'intérieur de la pompe, exprimer la puissance qu'elle fournit en fonction de et du débit volumique . Exprimer aussi le rendement propulsif défini comme la fraction de puissance utilisée effectivement pour l'acquisition d'impulsion de l'eau en sortie du canon.
  . Calculer et ; commenter.

II Canon à propulsion chimique

Une arme à propulsion chimique (qu'il s'agisse d'une arme légère ou d'une pièce d'artillerie) contient (figure 4) un projectile

, à symétrie de révolution, de rayon très légèrement inférieur au rayon

de l'âme du canon, de longueur

. Au moment de l'explosion, l'arrière du projectile (le culot) est disposé en

; entre ce culot et la culasse à l'arrière du canon se trouve la chambre de combustion de volume

dans lequel une certaine quantité de poudre sera, à l'instant

, portée à température suffisante (par exemple par percussion) pour en déclencher la combustion avec élévation de température et de pression; c'est celle-ci qui va propulser le projectile dans le tube du canon.

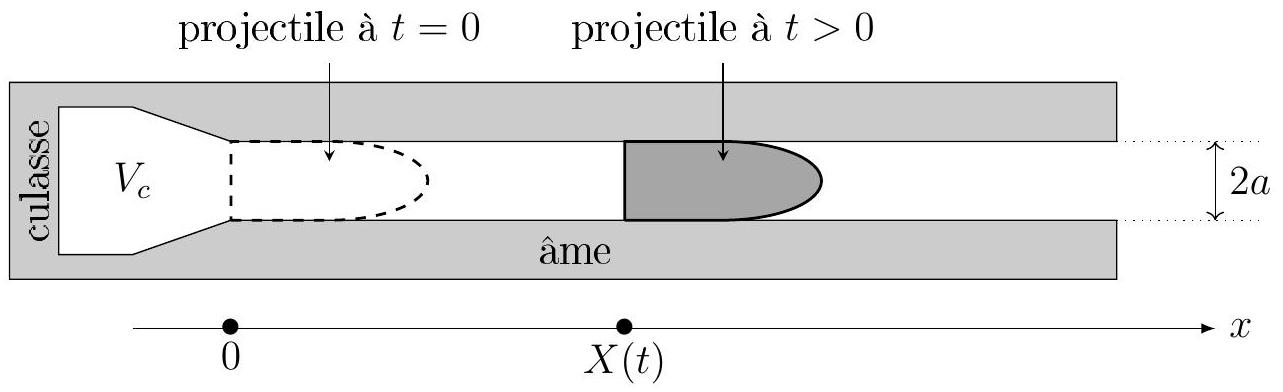
Figure 4 - Projectile dans un canon

Ainsi, pendant le mouvement du projectile, les gaz qui le propulsent occupent en arrière de celui-ci le volume

où

est l'abscisse du projectile, de masse

. On négligera toute fuite de ces gaz vers l'extérieur, qui sera considéré comme vide. On négligera aussi les forces de pesanteur.

II.A Le modèle des gaz de Joule

Tous les systèmes thermodynamiques étudiés seront décrits au moyen des variables intensives (pression

et température

) et des grandeurs extensives volume, énergie interne et entropie dont les valeurs molaires seront notées

. On rappelle, en dehors de toute transformation chimique ou changement d'état, l'identité thermodynamique associée à toute évolution infinitésimale :

Du fait des pression et température élevées régnant dans le canon, on ne peut se contenter d'un modèle de gaz parfait. On adoptera donc le modèle de Joule défini par deux caractéristiques (admises) :

le gaz vérifie la première loi de Joule : l'énergie interne molaire ne dépend que de la température;
l'entropie molaire du gaz a pour expression :

où

sont des constantes.

1. Déduire de (2) les expressions de (à une éventuelle constante additive près) et de l'équation d'état pour une quantité de matière en fonction des constantes et .
  À quelle(s) condition(s) ce modèle décrit-il un gaz parfait monoatomique? Attention, dans ce qui suit on ne se placera pas dans ce cas particulier.
1. Rappeler les définitions puis donner les expressions des capacités thermiques molaires et du gaz de Joule à volume et à pression constantes; commenter.
  On note la pression (très élevée) juste après la fin de la combustion, à lorsque le volume disponible pour le gaz est . On admet aussi que la combustion est instantanée et produit exclusivement un gaz de Joule, en quantité de matière . On suppose d'abord que la détente de ce gaz, pendant le mouvement du projectile dans le canon, est adiabatique et réversible.
1. Établir une relation liant, pendant une telle transformation, la pression et le volume molaire en fonction de et de .
  L'hypothèse isentropique est en fait peu réaliste et nous ne la conserverons pas dans ce qui suit. On considère donc ici, toujours dans le modèle du gaz de Joule, une évolution intérieurement réversible telle que le transfert thermique reçu par le gaz n'est plus nul mais donné par en fonction du travail des forces de pression, également reçues par le gaz.
  . Quel est, à votre avis, le signe de ?
  Établir la relation cte et exprimer l'exposant en fonction de et .
  - 11. Exprimer la force de poussée exercée sur le culot du projectile en fonction de , et .
1. Cette force est-elle conservative? Une réponse justifiée est attendue.

II.B Balistique intérieure

On étudie ici le seul cas d'un canon à âme lisse : le mouvement du projectile est seulement une translation et on peut négliger tous les frottements.

- 13. Établir l'équation différentielle du second ordre vérifiée par

- 14. Montrer que l'impulsion

acquise par le projectile à sa sortie du canon est donnée par la relation :

et exprimer

en fonction de

ainsi que

en fonction de

et de la température

des gaz à

. Commenter la signification et l'expression de

III Canon électromagnétique

Depuis la découverte des phénomènes d'induction, l'utilisation des forces électromagnétiques pour la mise en mouvement de projectiles a été souvent évoquée. Dès 1917, le français FAUCHONVilleplée réalise un prototype et dépose un brevet aux États-unis pour un tel canon (figure 5) : le projectile (f) est en contact électrique (e et e') avec deux rails conducteurs (g et g') qui permettent le passage du courant électrique généré par des batteries. Le projet a été repris pendant la seconde guerre mondiale en Allemagne puis par de nombreux pays depuis; l'agence de défense européenne (EDA) finance actuellement un projet de ce type (PILUM). Nous nous contenterons ici d'une étude de principe.

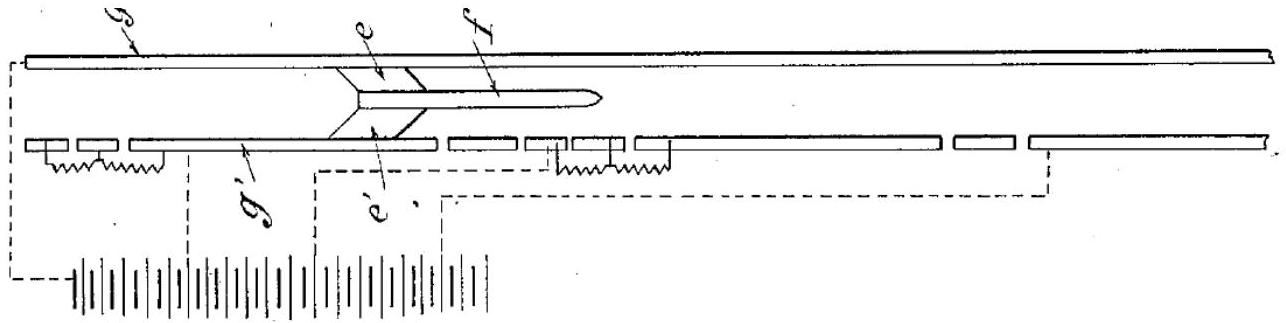
Figure 5 - Extrait du brevet US No 1370200

III.A Ordres de grandeur

Le canon électromagnétique repose sur la production d'un champ magnétique statique

par un courant électrique

circulant dans un circuit fermé. Nous utiliserons, à titre de modèle, le champ crée par un fil infini, cylindrique, confondu avec l'axe (

), parcouru par le courant

(figure 6). On caractérise un point

extérieur au fil par ses coordonnées cylindriques (

). On note

la perméabilité magnétique du vide.

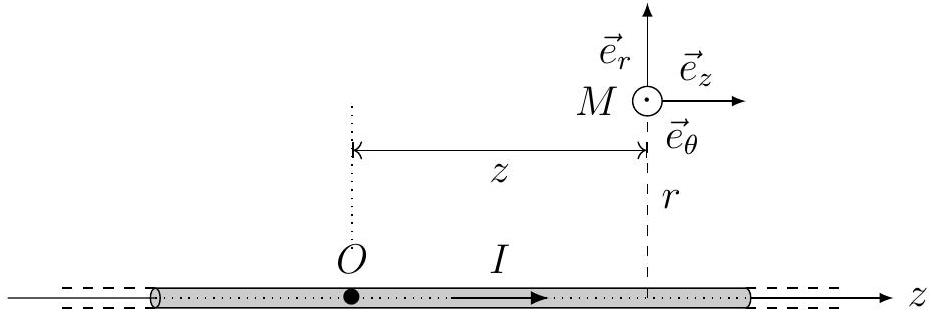
Figure 6 - Fil infini créant en

un champ magnétique

1. Déterminer la direction du champ magnétique créé en par ce fil. En déduire la projection de sur la base locale cylindrique en fonction des coordonnées de .

Dans l'expérience de 1917, un projectile de masse

est accéléré par un canon électromagnétique de longueur

et atteint à sa sortie l'impulsion

. L'écartement des rails est de l'ordre de

. En supposant l'accélération a constante à l'intérieur du canon, exprimer la durée

du tir en fonction de

puis

en fonction de

.
Dans le cas d'un tir en direction non horizontale, est-il légitime de négliger le poids du projectile?

1. Rappeler l'expression de la force de Laplace exercée sur un conducteur électrique.

En supposant le champ magnétique uniforme dans le canon, exprimer son intensité minimale

en fonction de

et du courant électrique

1. Ce champ magnétique est assimilé à celui créé par un fil infini situé à la distance du point où se trouve le projectile. Exprimer puis calculer la valeur minimale du courant électrique nécessaire à la réalisation de l'expérience, en fonction de et .
1. La résistance électrique du système est notée . On définit le rendement de propulsion comme le rapport de l'énergie cinétique emportée par le projectile à l'énergie électrique nécessaire au tir. Montrer que l'on peut mettre ce rendement sous la forme en exprimant la résistance utile en fonction de et . Sachant que , proposer une conclusion.

III.B Modélisation

La géométrie du propulseur et des rails d'alimentation est proposée figure 7 ; le générateur de tension constante

alimente l'ensemble en courant électrique depuis une abscisse

. La ligne est fermée par le projectile à l'abscisse

. Le mouvement de celui-ci démarre en

et se termine par l'éjection en

. La résistance électrique

du circuit, tout comme l'inductance propre

, dépendent a priori de la progression du projectile dans le canon. Le courant

est donc variable. On note

la masse du projectile et on néglige le poids et tous les frottements.

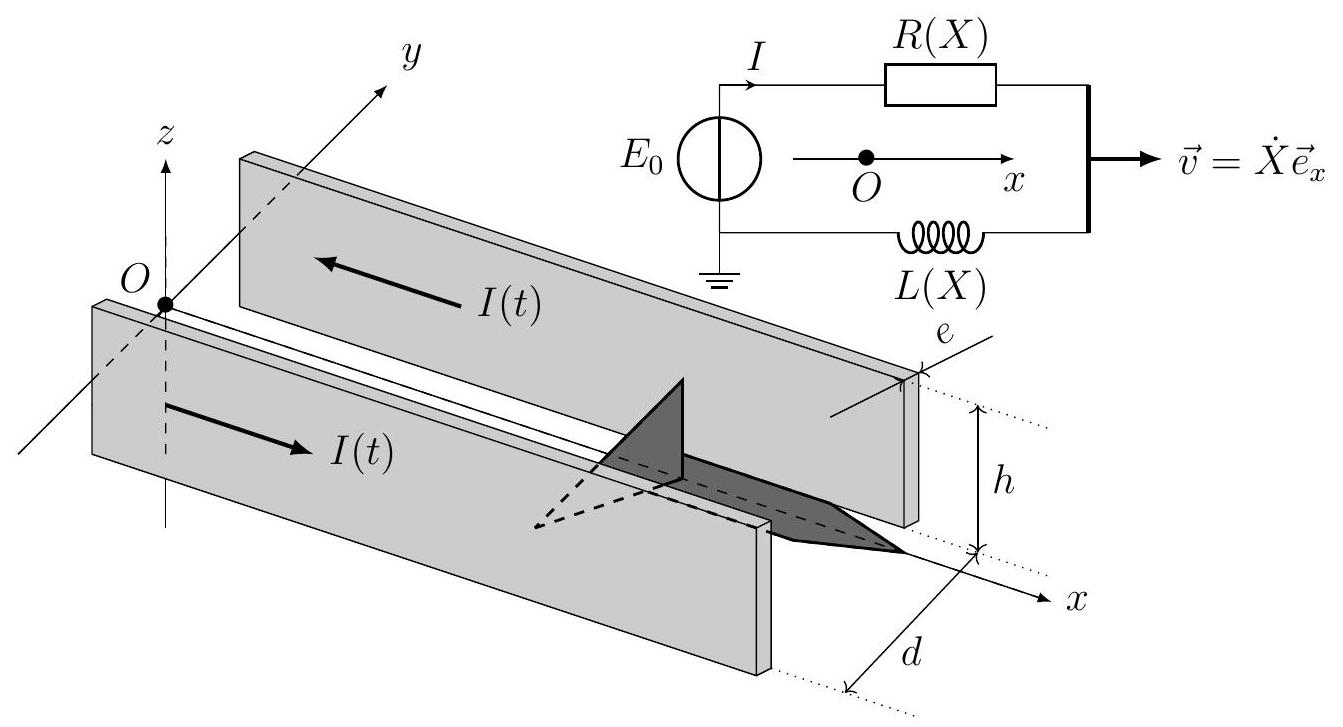
Figure 7 - Le propulseur d'un canon électromagnétique et son schéma équivalent

Les rails de guidage, distants de

, sont formés d'un matériau conducteur de conductivité

, de hauteur

et d'épaisseur

1. Rappeler la loi de Faraday de l'induction électromagnétique. On distingue parfois deux situations d'induction : «circuit fixe dans un champ magnétique variable» (induction de Neumann) et «circuit mobile dans un champ magnétique statique» (induction de Lorentz). Que dire de cette distinction dans le cas de la figure 7 ?
  - 21. Établir l'équation électrique reliant , les fonctions et leurs dérivées.
  . Justifier que la force propulsive est ; en déduire l'équation mécanique qui décrit le mouvement du projectile.
1. L'argument «la longueur des rails d'alimentation est , indépendamment de la position du projectile » pourrait servir à justifier un modèle où cte. En limitant votre argumentation à quelques lignes au maximum, expliquer pourquoi cet argument est incorrect.
  Dans la suite on négligera la résistance électrique du projectile et la résistance interne du générateur. Justifier le modèle linéaire, et exprimer en fonction des caractéristiques du rail de guidage.
  . En négligeant les effets de bord, on pourra en première approximation considérer le champ magnétique , dans le plan où se trouve le projectile, comme uniforme dans chaque zone de l'espace (entre les rails et hors de ceux-ci). Montrer, en précisant les hypothèses ou approximations nécessaires, qu'entre les rails il vaut ; on pourra s'inspirer du modèle du solénoïde infini.

En déduire l'expression de

.
Les équations différentielles du mouvement prennent la forme non linéaire ci-après, qui ne permet qu'une résolution numérique :

1. Exprimer les constantes positives et en fonction des données du problème. Préciser la dimension de et son interprétation physique.

FIN DE L'ÉPREUVE