Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé,
il le signale sur sa copie et poursuit sa composition en expliquant les raisons des
initiatives qu'il est amené à prendre.

Analyse physique d'un spa

La pandémie de COVID-19 a profondément changé la consommation de loisirs des français. N'étant pas sûrs de pouvoir voyager ou que les campings et plages soient accessibles, nombreux sont ceux qui ont cherché à se procurer du bien-être dans leur propre habitation en achetant une piscine ou un spa gonflable. Dans ce problème plusieurs aspects de l'utilisation du spa sont abordés, de la première installation au stockage hivernal.

Figure 1 - Photographie du spa étudié

Les applications numériques comporteront deux chiffres significatifs. Les données nécessaires à ces applications numériques et certaines définitions habituelles sont rassemblées en fin d'énoncé. Elles sont complétées par un formulaire. Les vecteurs sont généralement notés avec des flèches (

de norme

) et sont surmontés d'un chapeau s'ils sont unitaires (

I Installation du spa

I.A Gonflage

Le manuel d'utilisation fournit quelques données numériques :

Hauteur du spa gonflé sans couverture
Hauteur d'eau
Diamètre intérieur
Diamètre extérieur
Temps de gonflage
Seuil d'ouverture de la valve de surpression

L'enveloppe du spa se gonfle d'air, considéré comme un gaz parfait, grâce à une pompe contenue dans l'unité de contrôle. On considère que l'enveloppe prend sa forme définitive sans pli dès que la pression intérieure à l'enveloppe atteint la pression de l'air extérieur supposée égale à 1 bar. On ne prendra pas en compte l'épaisseur du tapis de fond en plastique du spa.

. Quel est le débit volumique moyen

de la pompe en litres par seconde?

1. Une fois gonflé en un temps , le volume du spa reste constant. Si l'utilisateur oublie d'arrêter la pompe, au bout de combien de temps la valve de surpression s'ouvre-t-elle? On supposera ici que la température de l'air dans l'enveloppe reste constante.
1. Le spa est gonflé en un matin à . En supposant que la pression extérieure et que le volume de l'enveloppe du spa restent constants au cours de la journée mais que la température extérieure peut augmenter, à partir de quelle température la valve de surpression s'ouvre-t-elle?

I.B Chauffage de l'eau

Le spa est équipé d'une unité de contrôle composée notamment d'une pompe de chauffage permettant de faire circuler l'eau à travers une source chaude. La vitesse de ce système de chauffage indiquée sur le manuel du spa est de

jusqu'à une température maximale de

1. Estimer la durée nécessaire pour atteindre la température maximale de depuis une température initiale de .
  La puissance de chauffage de l'unité de contrôle indiquée sur le manuel est : est-ce cohérent avec le résultat précédent?

Il est également possible de laisser naturellement chauffer l'eau du spa en plein soleil, sans utiliser la pompe de chauffage. Mais cela dépend de la météo, de l'heure d'exposition, et même a priori de l'altitude.

1. À quel moment de la journée le chauffage par le Soleil est-il le plus efficace? Justifier la réponse.

On cherche à savoir si l'eau chauffe plus vite en plein soleil si le spa est installé à haute altitude sans considérer une éventuelle baisse de la température due à cette élévation. Lorsqu'elle est éclairée par une onde électromagnétique

issue du rayonnement solaire, une molécule d'air (essentiellement

) se polarise selon le moment dipolaire

, avec

, où

étant respectivement la charge et la masse de l'électron.

. Justifier qualitativement le fait que l'on puisse écrire l'onde électromagnétique issue du rayonnement solaire sous cette forme.
Comment expliquer la création du moment dipolaire

? On se contentera d'une réponse qualitative.
On admet que chaque molécule d'air rayonne la puissance moyenne

. Montrer que, pour une pulsation donnée, l'éclairement (ici assimilé à la puissance surfacique moyenne) décroit selon l'axe de propagation du rayon solaire selon une loi du type

. On introduira

, le nombre de molécules d'air par unité de volume. Après avoir exprimé

en fonction de

on vérifiera la cohérence dimensionnelle de son expression.

1. Sachant que le maximum d'émission du Soleil est centré sur la longueur d'onde d'un rayonnement vert, estimer la valeur de .
  Sachant que l'épaisseur caractéristique de l'atmosphère est de l'ordre de 100 km , que peut-on dire de l'effet d'une augmentation d'altitude sur le chauffage de l'eau du spa?

II Utilisation du spa

II.A Pertes calorifiques

L'eau du spa est chauffée à

et le système de chauffage est arrêté. Le spa est installé sur la pelouse du jardin, que l'on assimile à une épaisseur

d'herbe tassée sous l'effet du poids. On suppose le sol et l'air extérieur à

. La température de l'eau variant très lentement, on se place en régime quasi stationnaire. Toutes les parties en contact avec l'air sont sièges d'échange conducto-convectif de coefficient

. On rappelle que la puissance s'écrit
dans ce cas

, où

est la surface d'échange et

l'écart de température sur cette surface. On néglige l'épaisseur de l'enveloppe en plastique du spa.

1. Définir la notion de résistance thermique.

Exprimer, en fonction des variables du problème, la résistance thermique de conduction des parois verticales du spa notée

(on se placera en symétrie cylindrique), ainsi que celle, notée

, du «tapis » d'herbe sous l'installation.

Les valeurs numériques avec un seul chiffre significatif de ces deux quantités sont respectivement

. On donne aussi celle de la résistance thermique due aux échanges convectifs entre l'eau et la paroi verticale du spa

ainsi que celle due aux échanges convectifs entre la surface de l'eau et l'air

1. Montrer que l'écart de température est de la forme et calculer le temps caractéristique dont on commentera la valeur.

Pour minimiser les pertes calorifiques et donc la consommation d'énergie, le manuel préconise de couvrir le spa à l'aide de sa couverture lorsque personne ne l'utilise, ainsi que de l'installer sur une toile de sol constituée d'un tapis de bulles d'air d'épaisseur

. Pour simplifier, on considère que la couverture du spa est gonflée d'air et qu'elle vient combler exactement l'espace entre la surface de l'eau et le haut du spa. Elle est donc d'une épaisseur constante

et elle recouvre l'intégralité du spa.

1. Estimer le gain obtenu sur le temps caractéristique en installant la toile de sol et la couverture.
1. La toile de sol et la couverture étant installées, quelle puissance faudrait-il fournir pour maintenir constante la température de l'eau du spa?

II.B Module de commande : maintien en température

L'unité de contrôle a besoin de mesurer la température pour assurer certaines fonctions comme son maintien automatique à une certaine valeur. Le principe est d'allumer et d'éteindre le module de chauffage avec des interrupteurs commandés.
La température de l'eau est mesurée à l'aide d'une thermistance. On peut modéliser ce composant par un cylindre métallique de section

, de longueur

, de conductivité électrique

et dont la résistance électrique

dépend de sa température.

1. Sans prendre en compte les effets de la température, en négligeant les effets de bords et en régime permanent, montrer que la résistance de ce cylindre serait $é$ .

Afin d'interpréter la dépendance de la résistance avec la température, on adopte le modèle de Drude qui consiste à appliquer la théorie cinétique des gaz aux électrons libres dans le métal. Ces derniers subissent des collisions aléatoires avec les ions beaucoup plus lourds et considérés immobiles.
Dans le modèle de Drude, chaque électron de vitesse

est soumis d'une part à la force due au champ électrique

supposé constant qui apparaît en appliquant une différence de potentiel aux extrémités du métal, et d'autre part, à une force de type frottement fluide

. Cette dernière permet de modéliser macroscopiquement l'effet d'un très grand nombre de collisions microscopiques aléatoires de moyenne nulle.

1. Montrer que la vitesse d'un électron est constante au bout d'un temps grand devant . En déduire une expression de la conductivité électrique en fonction de et de la densité volumique d'électron dans le métal.
1. En notant la vitesse d'un électron juste après une collision à l'instant , comment s'exprime sa vitesse juste avant la collision suivante plus tard?
  En moyennant le résultat sur un très grand nombre de collisions, proposer une interprétation physique pour .
  En déduire que la résistance du métal augmente lorsque sa température augmente.
  Dans la suite, on notera la résistance de la thermistance en cuivre à la température , avec et .
  On s'intéresse au mode «maintien de température » de l'unité de contrôle, utilisé lorsque l'eau du spa a déjà été chauffée à la température souhaitée . Ce mode maintient la température dans l'intervalle [ ], où . On a donc besoin de deux interrupteurs commandés en température. Un montage possible pour un interupteur est donné sur la figure 2, où les deux générateurs de tension constante sont identiques. L'Amplificateur Linéaire Intégré (ALI) idéal fonctionne ici en saturation, il n'a que deux tensions de sorties possibles ce qui permet de commander la fonction d'un interrupteur.
  . Pour quelle valeur de la température, l'interrupteur (caractérisé par ) change-t-il d'état? On exprimera en fonction de et .
  On suppose et parfaitement déterminés, quelle précision relative est nécessaire sur pour régler la température au degré près?

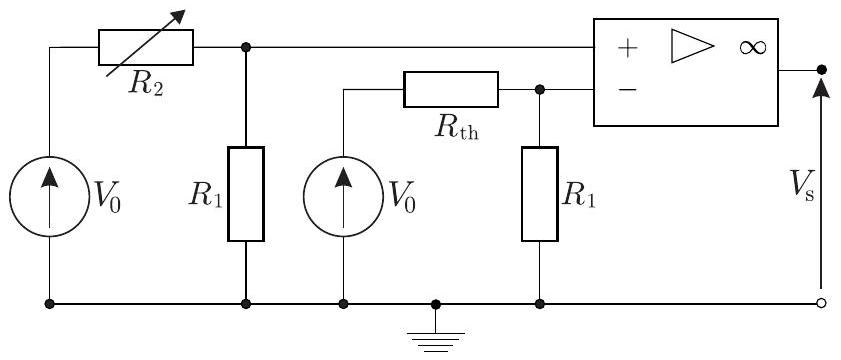
Figure 2 - Interrupteur à amplificateur linéaire

1. Expliquer comment organiser deux interrupteurs commandés qui permettent de maintenir la température dans l'intervalle .

II.C Brassage de l'eau

Nous cherchons à modéliser dans cette partie la façon dont les bulles d'air produites au fond du spa permettent de brasser l'eau qu'il contient et de générer ainsi une sensation de relaxation à son utilisateur.

1. En faisant l'hypothèse que la température des bulles d'air est constante, quelle est la variation de volume relative d'une bulle due à la pression hydrostatique?
  En déduire que le volume d'une bulle peut être considéré constant au cours de sa remontée vers la surface.

On note

le rayon d'une bulle qui, lors de sa remontée à la vitesse de module

, subit une force de trainée

de module

. Sur la figure 3 ci-après, on définit le coefficient de trainée

et on trace sa représentation graphique en fonction du nombre de Reynolds Re. On précise que pour des faibles valeurs du nombre de Reynolds (régime de Stokes), la courbe peut être approximée par

- 19. On considère une bulle de taille caractéristique

remontant à une vitesse de l'ordre de quelques dizaines de centimètres à un mètre par seconde, estimer le nombre de Reynolds correspondant. Comment s'exprime la force de trainée dans ce régime?

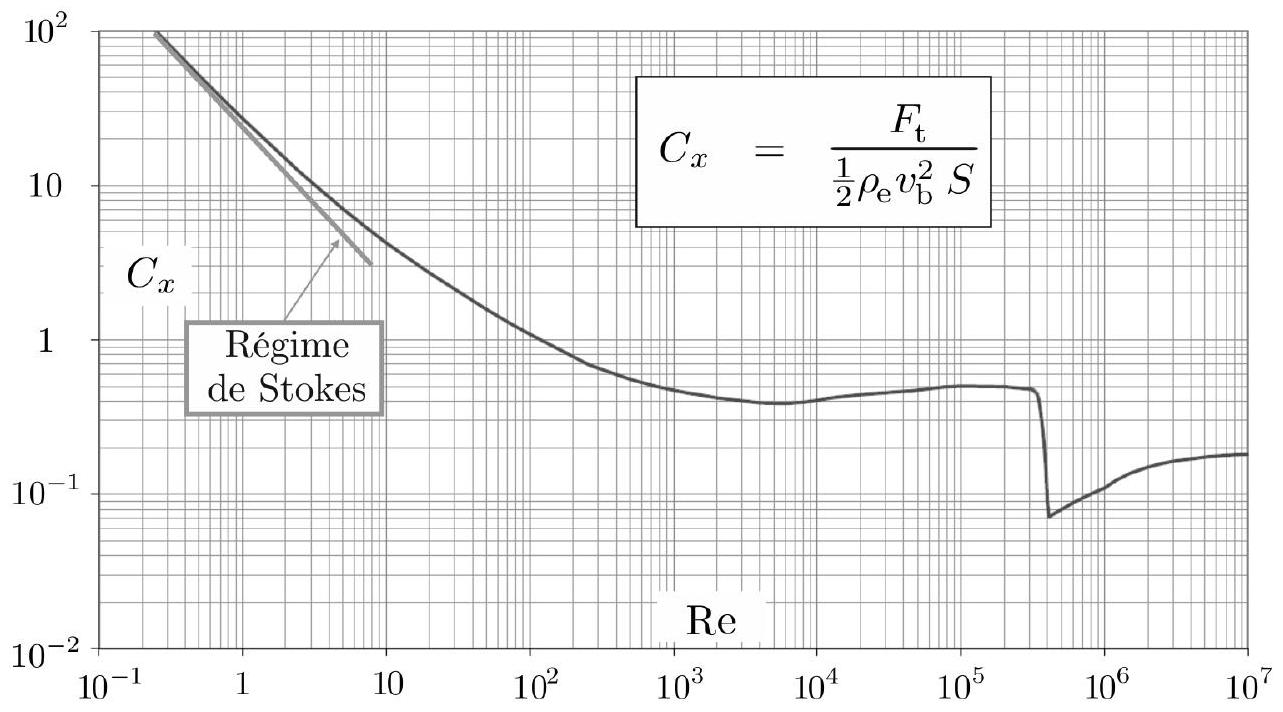
Figure 3 - Coefficient de trainée (

) en fonction du nombre de Reynolds pour une bulle de section

dans la direction de l'écoulement, subissant une trainée

et se déplaçant à une vitesse de module

dans de l'eau de densité

1. En supposant que la bulle est lâchée sans vitesse initiale au fond du spa, exprimer sa vitesse sous la forme où est une fonction trigonométrique hyperbolique et dans laquelle on exprimera la vitesse en fonction de et et la durée en fonction de et .
  Comment s'interprètent et ?
  Numériquement on trouve et , commenter l'adéquation du modèle avec ces valeurs.

On se place dans la situation dans laquelle une bulle d'air ne subit plus aucune accélération. Le référentiel lié à cette bulle est donc galiléen.
Dans un modèle simple on ne considère pas les variations dues à la pression hydrostatique et on cherche à montrer que la pression et le volume de la bulle ne sont constants qu'en moyenne, et que c'est leur variation sur une échelle de temps courte qui permet de transférer de l'énergie à l'eau qui l'entoure.

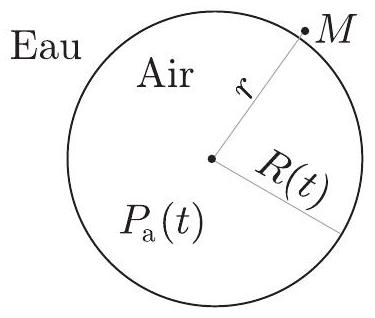
Figure 4 - Modèle pour la bulle

On ne considère pas non plus les interactions entre les bulles : on étudie une seule bulle fixe, de rayon

variable, entourée d'eau jusqu'à l'infini (la taille du spa est très grande devant celle d'une bulle). On néglige également les effets dus à la viscosité de l'eau ainsi que ceux dus à la diffusion thermique par rapport aux termes de pression interne. On suppose que le rayon de la bulle varie peu : on note

avec

étant le rayon de la bulle si

où

bar est la pression atmosphérique et

celle à l'intérieur de la bulle.

1. En supposant l'écoulement de l'eau autour de la bulle incompressible, déterminer l'expression de la vitesse d'un point quelconque situé dans l'eau, à une distance du centre de la bulle et au voisinage de sa surface, en fonction notamment de .
  La conservation de l'impulsion autour de la bulle permet d'établir la relation

1. En déduire qu'à l'ordre le plus bas en on peut écrire

On exprimera

en fonction de

.
À partir de cette relation, obtenir une expression de la pression

à l'intérieur de la bulle en supposant que la pression dans l'eau loin de la bulle est égale à

1. En considérant que la bulle évolue de façon isentropique, obtenir une autre relation entre et .
1. Montrer alors que le rayon de la bulle oscille et calculer la fréquence correspondante. On prendra .
  En estimant le temps caractéristique de diffusion thermique dans la bulle, montrer que l'hypothèse d'évolution isentropique est cohérente.
1. Estimer l'énergie cinétique moyenne associée à ces oscillations.

Conclure sur le brassage de l'eau provoqué par les bulles du spa.

À toutes fins utiles...

Données physiques

Masse de l'électron :
Charge de l'électron :
Accélération de la pesanteur :
Permittivité diélectrique du vide :
Perméabilité magnétique du vide :
Constante d'Avogadro:
Constante molaire des gaz parfaits :

Pour l'eau considérée dans le sujet on prendra

Masse volumique :
Capacité thermique massique :
Viscosité dynamique (supposée indépendante de la température) :

Pour l'air considéré dans le sujet on prendra

Conductivité thermique :
Coefficient d'échange conducto-convectif :
Masse volumique :
Coefficient adiabatique :
Capacité thermique massique à volume constant :

Pour l'herbe considéré dans le sujet on prendra:

Conductivité thermique :

Formulaire

Pour les fractions de cercles on prendra et .
On rappelle que

La divergence d'un vecteur dont les coordonnées sont ( ) dans la base ( ) des coordonnées sphériques s'écrit :

FIN DE L'ÉPREUVE

Les sujets sont la propriété du GIP CCMP. Ils sont publiés sous les termes de la licence
Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 3.0 France.
Tout autre usage est soumis à une autorisation préalable du Concours commun Mines Ponts.

Mines Physique 1 PSI 2024

A2024 - PHYSIQUE I PSI

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL. Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).