Version interactive avec LaTeX compilé
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURS DE L'AÉRONAUTIQUE ET DE L'ESPACE DE TECHNIQUES AVANCÉES, DES TÉLECOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE ÉCOLE POLYTECHNIQUE (FILIERE TSI) CONCOURS D'ADMISSION PREMIÈRE ÉPREUVE DE PHYSIQUE
Filière PSI
(Durée de l'épreuve :
Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPEEIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
Physique I - Filière PSI
L'énoncé de cette épreuve, particulière aux candidats de la filière PSI, comporte 6 pages.
(Durée de l'épreuve :
Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPEEIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
Physique I - Filière PSI
L'énoncé de cette épreuve, particulière aux candidats de la filière PSI, comporte 6 pages.
- Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
- Il ne faudra pas hésiter à formuler tout commentaire qui vous semblera pertinent, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.
La surface de la Lune
On se propose d'étudier quelques aspects de la surface lunaire : la température de surface, le sol et l'atmosphère. Les diverses parties sont indépendantes entre elles.
- Important : on trouvera en page 6 un ensemble de données relatives à ce problème; ces données complètent (ou, à l'occasion, répètent) celles de l'énoncé. Quelques-unes de ces données pourront servir plusieurs fois; d'autres n'ont de valeur qu'informative. Quand l'énoncé ne les indique pas, il appartient aux candidats de repérer et d'utiliser les données utiles pour la résolution de certaines questions.
- Les questions numérđées avec un astérisque (par exemple 1*) sont de type essentiellement qualitatif ; elles demandent peu de calculs, voire pas du tout.
I Détermination expérimentale de la température lunaire
Mesures
On effectue cette détermination à l'aide d'un télescope à miroir sphérique de rayon
est supposé ponctuel.
Deux mesures sont effectuées, la première avec un filtre qui absorbe l'infra rouge, et la seconde sans filtre. La différence entre les deux mesures permet d'estimer la température superficielle de la région lunaire étudiée.
2* - Où doit-on placer le détecteur?
est supposé ponctuel.
Deux mesures sont effectuées, la première avec un filtre qui absorbe l'infra rouge, et la seconde sans filtre. La différence entre les deux mesures permet d'estimer la température superficielle de la région lunaire étudiée.
2* - Où doit-on placer le détecteur?
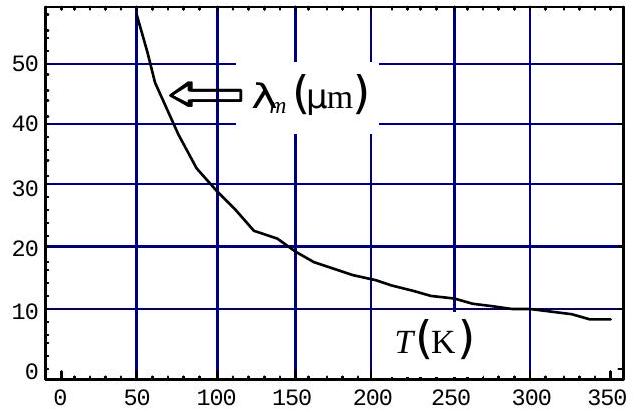
Fig. 2 : Maximum d'émission
3* - Admettons ceci: la puissance lumineuse émise à la température
- 4* - Le diamètre d'ouverture,
, des télescopes observant la surface lunaire est de l'ordre du mètre. Estimer la résolution de la mesure effectuée depuis un télescope terrestre ou en orbite terrestre. On rappelle que la résolution angulaire d'un télescope correspond au rayon angulaire de la tâche d'Airy, soit .
Interprétation des résultats
Les températures maximales du sol lunaire sont d'environ
- 6 - Décrivez sur un schéma les zones de pénombre et d’ombre relativement au Soleil et à la Terre, lorsque la Terre éclipse le Soleil. Évaluer les durées respectives de pénombre et d'ombre.
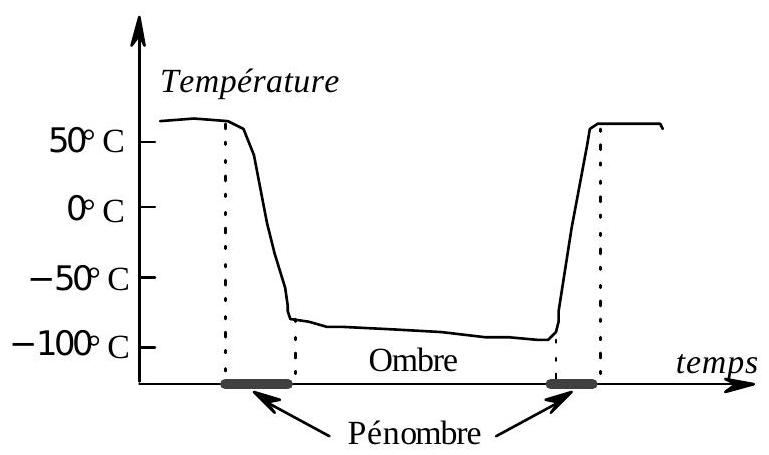
Fig. 3 ; cycle de température lunaire qualitatif entre la courbe et le modèle.
II Le sol lunaire
Modélisations
Le sol lunaire est bombardé et réduit en poussière par les météorites et le vent solaire, constitué essentiellement de protons et d'électrons. La composition du sol lunaire est proche de celle des silicates, dont quelques caractéristiques physiques sont indiquées page 6. La couche supérieure, très fine, peut être représentée par un empilement compact de sphères de silicates, de rayon
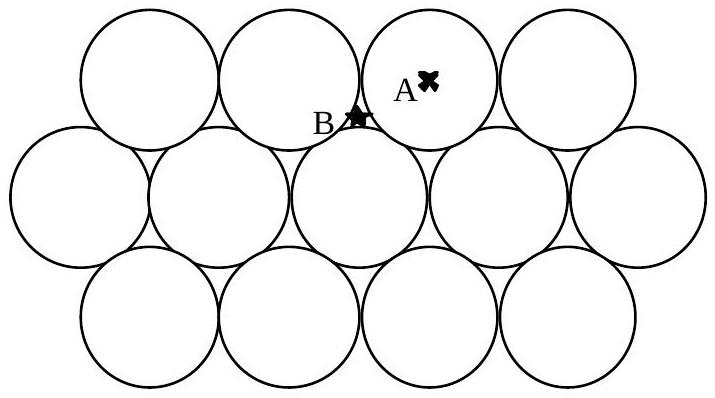
Fig. 4 : Le plan inférieur de l'empilement compact est constitué de sphères dont les centres sont notés
- 9*- L’empilement précédent est maintenant modélisé par un ensemble de plans parallèles opaques, placés dans le vide, séparés par la distance
. Que pensez-vous de ce modèle ?
- On peut caractériser un tel milieu par un coefficient de conductivité thermique dépendant de la température de la forme , avec . Comparer l’ordre de grandeur de obtenu avec ce modèle à la valeur expérimentale de la conductivité des silicates à la température ambiante : ,
- Comparer la densité et la capacité calorifique massique de la couche supérieure avec et .
12* - Il est généralement admis que ce sont les couches les plus profondes qui ont les caractéristiques physiques les plus voisines de celles des modèles ci-dessus. Pourquoi ?
Influence de l'impact des météorites
On admet que les météorites heurtant la surface lunaire ont même composition que le sol lunaire. On rappelle que le référentiel de Copernic, ou référentiel héliocentrique, est lié au centre de masse du système solaire et que ses axes pointent vers des étoiles réputées fixes. Le référentiel de Copernic est supposé galiléen.
14- Montrer que l'impact d'une météorite de masse
15* - La solidification du matériau en fusion n'est pas sans effet sur la nature des transferts thermiques ultérieurs. Vers quelle valeur se rapproche alors la conductivité thermique calculée précédemment ?
III Atmosphère lunaire.
Absence d'atmosphère gazeuse
Un gaz parfait, possédant par unité de volume
- 16 - L'atmosphère lunaire est majoritairement composée d'atomes d'argon, libéré lors des réactions nucléaires au sein des roches lunaires. Sachant que la masse molaire
de ce gaz vaut 40 g , et en utilisant l'équation des gaz parfaits, calculer pour .
- On note la vitesse de libération lunaire; c'est la vitesse minimale d'un objet pouvant échapper à l'attraction gravitationnelle lunaire. Exprimer puis calculer la vitesse de libération lunaire. En déduire qu’une atmosphère lunaire ne saurait subsister.
Étude d'une atmosphère «ionique». Méthode de l'occultation
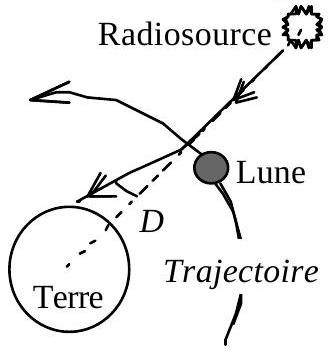
Fig. 5 : Déviation d'un rayon lumineux près de l'occultation
On suit depuis un radiotélescope terrestre le rayonnement émis par une radiosource monochromatique lointaine, supposée immobile par rapport à la Terre, et située dans le plan de l'orbite lunaire. Cette source peut être occultée provisoirement par la Lune (Fig. 5). La durée mesurée de l'occultation est supérieure à la valeur attendue pour une Lune qui ne possèderait pas d'atmosphère. L'écart
La courbure du rayon lumineux est attribuée à une variation continue de l'indice
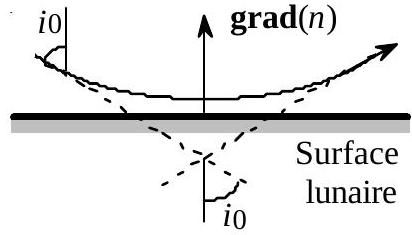
Fig. 6 Détail de la déviation
18* - Justifier, en considérant la courbure du rayon lumineux, que la variation de l'indice avec l'altitude a bien le sens indiqué dans la figure 6. Quelle est, en admettant, (comme indiqué Fig. 6) que le rayon rase la surface lunaire, la relation entre
19 - Soit
- 21 - Dans le domaine hertzien, l'indice d'une atmosphère ionique, constituée d'électrons de charge (
), de masse et de concentration suffisamment faible s'écrit , où est la permittivité électrique du vide et où est le carré de la pulsation de plasma. Déterminer la valeur numérique de la pulsation de plasma pour la Lune, sachant que la fréquence de la radiosource est .
- Pour la Terre, rad.s . Déterminer la densité volumique de l'atmosphère lunaire. On a coutume d'assimiler ces électrons à un gaz parfait ; est-ce légitime ?
23* - Comparer la durée de l’occultation dans le domaine du visible et dans le domaine des ondes radio. Pourquoi utilise-t-on préférentiellement le domaine radio pour étudier l'atmosphère lunaire ?
25 - À partir de la définition de la norme du vecteur d’onde
25 - À partir de la définition de la norme du vecteur d’onde
Fin du problème
Données numériques
Soleil
- Rayon
- Température de surface
Terre
- Rayon terrestre
- Distance Terre-Soleil
- Masse terrestre
- Période du mouvement circulaire autour du Soleil
jours
Lune
- Rayon lunaire
- Masse lunaire
- Distance Terre-Lune
- Période du mouvement circulaire autour de la Terre
jours (en restant dans le plan de l'orbite terrestre) - Période de rotation propre de la Lune
jours . La Lune présente ainsi toujours la même face à la Terre.
Silicates
- Densité
- Conductivité thermique
- Chaleur spécifique
- Ordre de grandeur du rayon
- Température de fusion du silicate
- Chaleur latente de fusion
Constantes physiques
- Célérité de la lumière dans le vide
- Constante de la gravitation
- Constante de Planck
- Constante de Boltzmann
- Charge électrique élémentaire
- Masse de l'électron
- Nombre d'Avogadro
- Permittivité du vide
F. - Constante des gaz parfaits
