J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Physique 1 PC 2000

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2000
Filière
PC
Matière
Physique
Mines PCMines 2000PC PhysiquePhysique 2000
2025_09_04_38184a5811a65318c3c9g

A 00 PHYS. I

ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE, ÉCOLE POLYTECHNIQUE (FILIÈRE TSI)
CONCOURS D'ADMISSION 2000
PREMIÈRE ÉPREUVE DE PHYSIQUE
Filière PC
(Durée de l'épreuve : heures; l'emploi de la calculatrice est autorisé)
Sujet mis à disposition du concours ENSTIM, INT, TPE-EIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
PHYSIQUE I -PC
L'énoncé de cette épreuve, particulière aux candidats de la filière PC, comporte 8 pages.
  • Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
  • Tout résultat fourni dans l'énoncé peut être utilisé pour les questions ultérieures, même s'il n'a pas été démontré.
  • Il ne faudra pas hésiter à formuler les commentaires (incluant des considérations numériques) qui vous sembleront pertinents, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.
L'épreuve comprend deux problèmes indépendants entre eux, et qui pourront être traités dans l'ordre que l'on voudra. Le premier étudie l'irréversibilité d'une évolution, le second s'intéresse à une manière de tendre vers la réversibilité. Les diverses parties de ces problèmes sont liées par le sens et certains de leurs résultats sont analogues.

PROBLÈME I : IRRÉVERSIBILITÉ ET FONCTION G*

Toute évolution spontanée d'un système quelconque génère une création d'entropie. Quand le système est en interaction avec une source unique, l'irréversibilité de la transformation est calculable à partir d'une fonction, nommée . Le problème présente cette fonction successivement pour un fluide parfait homogène, pour un fluide diphasé et pour une particule en mécanique.

1. Cas du Fluide Parfait

1.1. Déséquilibre mécanique

Un corps de pompe horizontal contient une mole de gaz parfait dans les conditions de
température et de pression et . La capacité calorifique molaire du gaz à pression constante est constante. Le piston et le corps de pompe sont de bons conducteurs thermiques (parois diathermanes).
L'atmosphère extérieure est une source d'énergie thermique et de travail. Sa température est notée et sa pression . Elle peut ainsi, d'une part échanger une quantité finie d'énergie thermique (" chaleur ") sans voir varier sa température, d'autre part changer de volume sans que sa pression varie. Le piston (fig. 1) est débloqué à l'instant ; on attend l'équilibre final. Les frottements du piston sont négligés.
Fig. 1 : piston, à _
- Établir l'expression de la variation d'entropie d'une mole de gaz parfait, subissant une transformation réversible entre deux états 1 et 2 (on note la constante des gaz parfaits, ou constante molaire) :
- Quelle est la variation de l'entropie du gaz ? Quelle est son signe selon que ou ? L'évolution du gaz n'est-elle pourtant pas irréversible dans les deux cas ?
- Calculer la variation de l'entropie de l'Univers et exprimer cette dernière en fonction de . À l'aide d'une étude graphique, déterminer le signe de dans les deux cas et . On pourra poser, ici et ailleurs,

1.2. Déséquilibre thermique

Fig. 2 : -; éléments isolés
La géométrie du système est la même que la précédente, mais le piston et le corps de pompe sont maintenant recouverts d'un isolant thermique. Le gaz est dans les conditions de température et de pression . Le piston est libéré à l'instant et l'isolant est supprimé (figure 2).
- Exprimer la variation de l'entropie du gaz en fonction de et de .
- Toujours en procédant graphiquement (poser ), calculer la variation d'entropie de l'Univers ; déterminer son signe dans les deux cas ou .

1.3. Déséquilibre thermodynamique

Dans les conditions initiales les plus générales, on note la température du gaz et sa pression ; le gaz est isolé thermiquement, le piston est bloqué. À l'instant , le piston est libéré et l'isolant supprimé.
- Exprimer et commenter l'expression de en fonction de et .

1.4. La fonction

On considère (fig. 3) la transformation la plus générale où le gaz est en déséquilibre thermodynamique aux deux instants initial et final. Pratiquement, on bloque le piston avant
que l'équilibre mécanique soit atteint et on remet en place l'isolant thermique. Le gaz est alors dans l'état ( ).
On définit la fonction par où et désignent respectivement l'énergie interne et le volume du gaz.
- On note et les variations de volume et d'entropie de la source. Exprimer la variation d'énergie interne de la source au cours de la transformation en fonction de , et .
- Exprimer la variation d'entropie de l'Univers en fonction de . En déduire que mesure l'irréversibilité de la transformation. Quel est l'intérêt de la fonction par rapport à pour ce type d'interaction ? Justifier le nom de potentiel thermodynamique donné à .
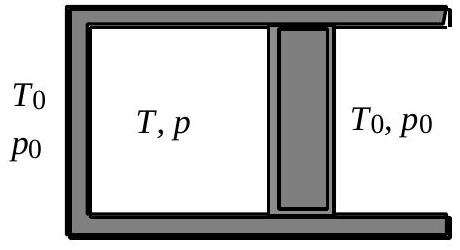
Fig. 3a : état initial
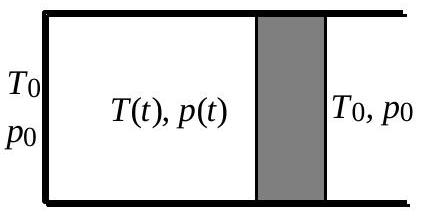
Fig. 3b : état intermédiaire
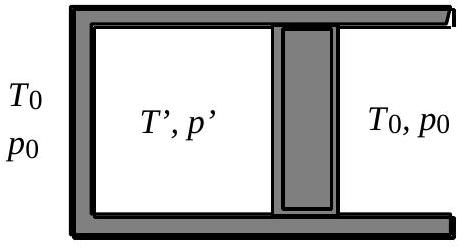
Fig. 3c : état final
8 - La situation de déséquilibre mécanique (section 1.1) est définie par , celle du déséquilibre thermique (section 1.2) par . Quelle est, selon la mesure introduite à la question 7, la transformation la plus irréversible ?

2. Cas d'un système diphasé

La figure 4a décrit la situation : à l'instant , le corps de pompe, isolé thermiquement, contient 1 mole d'eau à la température . Le piston est bloqué et le volume intérieur est . La température de l'atmosphère extérieure est , sa pression est (pression atmosphérique). On suppose que le volume de l'eau liquide est négligeable et que l'eau vapeur se comporte comme un gaz parfait.
À la pression de vapeur saturante de l'eau est et la chaleur latente de vaporisation vaut ; la constante molaire est .
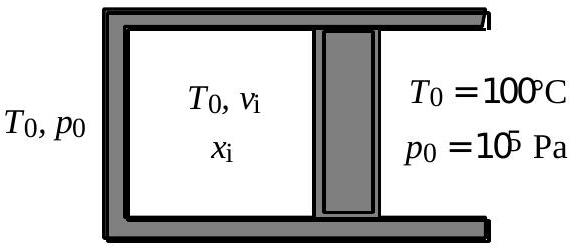
A l'instant , le piston est libéré. On bloque ce dernier lorsque le volume intérieur atteint la valeur (fig. 4b).
Fig. 4a : état initial
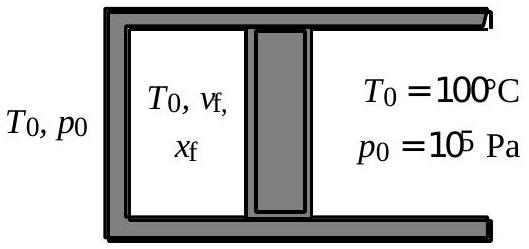
Fig. : état final
9 - Déterminer les titres molaires initial et final en vapeur d'eau. Il sera commode de formuler une hypothèse, que l'on vérifiera, sur l'état initial de l'eau dans le corps de pompe.
10 - Exprimer littéralement puis numériquement les variations d'énergie interne et d'entropie d'une mole d'eau se vaporisant à la température de . En déduire la variation entre les états initial et final. Commenter.
11 - Le piston est à nouveau débloqué. Que se passe-t-il ? On déplace alors très lentement le piston jusqu'à ce que le volume occupé par l'eau soit . Quelle est la nouvelle variation de la fonction ? Comparer cette variation à la variation d'enthalpie libre de l'eau au cours de la même transformation.

3. Thermodynamique du mouvement unidimensionnel d'une particule

En mécanique classique comme en mécanique relativiste, la loi fondamentale de la dynamique dans un référentiel galiléen appliqué à une particule en mouvement sur un axe sous l'action d'une force s'exprime sous la forme . On considère un gaz de particules identiques et équivalentes et on s'intéresse à l'une d'entre elles, représentative de l'ensemble. L'équation d'état de cette particule, c'est-à-dire la relation liant la quantité de mouvement à la vitesse est supposée, à ce stade, inconnue. La particule représentative est en interaction avec une source de chaleur de température et une source de vitesse (cette source peut échanger une quantité de mouvement finie sans changer de vitesse). La température de la particule est notée .
12 - Montrer que les différentielles des énergies internes de la particule, , et de la source (dont les grandeurs sont affectées de l'indice " s "), s’écrivent respectivement
13 - Par analogie avec les exemples précédents, on définit la fonction de la particule par : . Montrer que la variation de au cours de l'interaction parti-cule-source est reliée à l'entropie crée par la relation .
14 - On suppose à partir de maintenant que le mouvement est unidimensionnel ; les grandeurs et sont des scalaires. L'expression à l'ordre le plus bas de la variation élémentaire de pour des variations élémentaires et est
Exprimer dans le cas général et en fonction de , et ; en déduire les grandeurs et d'équilibre de la particule.
- Quelle est alors, à l'ordre le plus bas, la forme de l'expression de d autour de l'équilibre ? Exprimer et à l'équilibre en fonction de dérivées premières de et de .
-En déduire le sens de variation de l'entropie avec la température ainsi que le sens de variation de la quantité de mouvement avec la vitesse.
-En mécanique classique, l'équation d'état est évidemment compatible avec le sens de variation de la fonction établi à la question 16 ; qu’en est-il en mécanique relativiste où ?

Fin de ce problème

PROBLÈME II : UNE APPROCHE DE LA RÉVERSIBILITÉ

La mole de gaz parfait considérée dans cette partie est caractérisée par son coefficient , rapport des chaleurs massiques à pression et à volume constant, supposé indépendant de la température. La constante des gaz parfaits est notée . Pour chacune des évolutions du gaz, l'état initial sera l'état d'équilibre, caractérisé par les grandeurs ( ) pression, volume, température ; on cherchera chaque fois à limiter la production d'entropie associée à l'évolution.

3. Étude d'une transformation monotherme

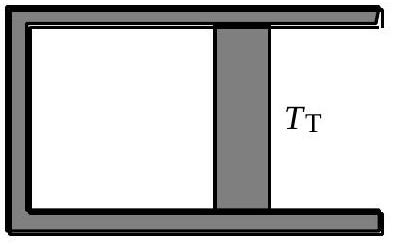
Fig. 5 : évolution monotherme
18 - Le gaz parfait est placé dans un récipient à parois fixes. Une des parois est mise en contact avec un thermostat dont la température est notée . Les autres parois sont calorifugées (fig. 5). Déterminer l'état final ( ) du gaz quand, à l'issue de la transformation, l'équilibre est atteint. Effectuer un bilan d'entropie. La transformation est-elle thermiquement réversible?
19 - On réalise la transformation précédente en mettant la paroi non calorifugée du récipient contenant le gaz avec une succession de sources dont les températures respectives sont (ce qui définit ). On a de la sorte et . Définir l'état final du gaz à l'issue de cet ensemble de transformations. Effectuer un bilan entropique pour la transformation élémentaire . En déduire, pour la transformation totale, l'expression de la quantité d'entropie liée à une éventuelle irréversibilité thermique de la transformation.
- Cette quantité d'entropie peut-elle s'annuler lorsque est assez grand (en toute rigueur, ) ? on rappelle que .

4. Étude d'une transformation monobare

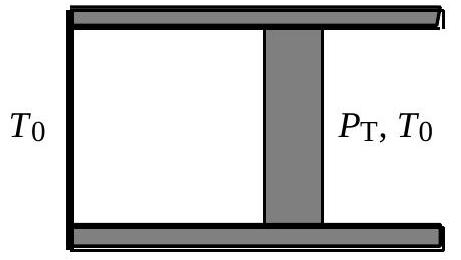
Fig. 6 : évolution monobare
21 - Le gaz parfait est initialement en contact avec une source à la température , dans un récipient dont les autres parois sont calorifugées (fig. 6). Une de ces parois, initialement bloquée, peut se déplacer sans frottement. On libère la paroi mobile, la pression extérieure, constante, est notée . Déterminer l'état final ( ) du gaz quand, à l'issue de la transformation, l'équilibre est atteint. Effectuer un bilan d'entropie. La transformation est-elle thermiquement réversible ?
22 - On réalise la transformation précédente en déplaçant la paroi mobile par étapes successives. À l'étape , la pression du gaz est , de sorte que et . Avec , cela définit l'incrément de pression . Définir l'état final du gaz à l'issue de la transformation complète. Effectuer un bilan entropique pour la transformation élémentaire . En déduire, pour la transformation totale, la quantité d'entropie liée à une éventuelle irréversibilité mécanique de la transformation.
23 - Cette quantité d'entropie peut-elle s'annuler?

5. Étude d'une transformation plus générale

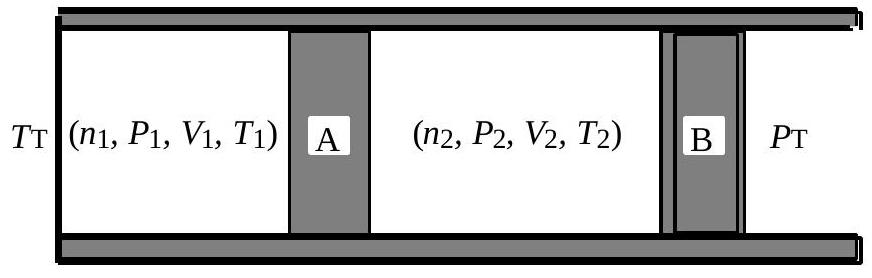
Fig. 7: Évolutions de gaz parfaits
La figure 7 illustre la situation initiale du système. La paroi A est diathermane. Les parois latérales et la paroi B sont calorifugées. Cette dernière, initialement bloquée, peut se déplacer sans frottement. La pression extérieure, notée , est constante. La transformation consiste à mettre le gaz 1 en contact avec la source à la tempé
rature et à libérer la paroi B .
  • 24 - Déterminer l’état final de chacun des deux gaz. Faire un bilan d’entropie.
    - Analyser la nature d'éventuelles irréversibilités.
  • 26 - Est-il possible, tout en arrivant aux mêmes états finaux, de diminuer l'entropie créée?

6. Au-delà du gaz parfait...

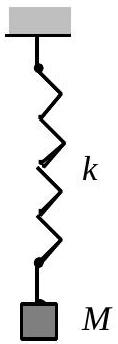
Un ressort élastique de raideur est chargé en étapes par une masse ; à chacune des étapes, une masse est ajoutée au système, et la longueur du ressort augmente de . Au total, la longueur du ressort a augmenté de . On rappelle la formule sommatoire : .
Fig. 8 : Ressort élastique
27 - Calculer la variation d'énergie potentielle associée au chargement progressif du ressort, calculer la variation d'énergie élastique et en déduire l'expression de l'énergie dissipée sous forme thermique.
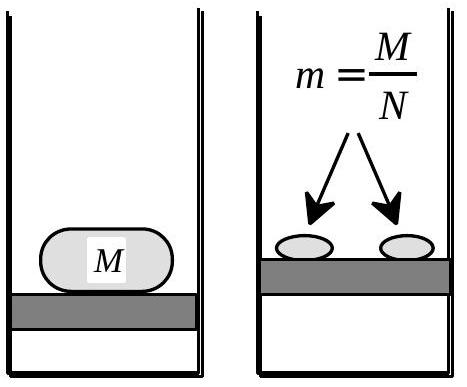
- La température du milieu est constante, calculer la variation d'entropie associée au processus.
- Un condensateur de capacité est chargé sous une différence de potentiel en étapes identiques. À chacune des étapes, la différence de potentiel entre les armatures est augmentée de , par le branchement d'une source d'alimentation supplémentaire. La température est constante. Calculer l'énergie totale perdue par les sources, l'énergie électrostatique accumulée dans le condensateur et montrer que l'augmentation d'entropie liée à ce processus est .
Fig. 9 : Compression d'un gaz parfait
Une mole de gaz parfait en contact avec un thermostat à la température est comprimée de la pression à la pression , son volume varie de à . Lorsque la transformation est soudaine, comme c'est le cas par exemple si l'on pose sur le piston un objet de masse appropriée, le système se stabilise après quelques oscillations amorties. L'énergie thermique dissipée dans le milieu extérieur est .
- Exprimer la variation d'entropie du thermostat, , et celle du gaz, . Exprimer la variation totale d'entropie en fonction de et des pressions initiale et finale.
-Exprimer la variation totale d'entropie lorsque le processus est réalisé en étapes.
- Dans le cas où , simplifier l'expression de la variation d'entropie établie à la question 31.
- Montrer que, désignant la charge du condensateur sous une tension et le volume du piston sous une pression , la relation et la relation analogue pour le piston peuvent être mises respectivement sous les formes
En comparant R1 et R2, proposer une analogie entre les deux systèmes et leurs variables caractéristiques ; étayer cette analogie par un argument énergétique et justifier qualitativement la différence des signes qui figurent dans ces deux relations.

Fin de ce problème

FIN DE L'ÉPREUVE

Mines Physique 1 PC 2000 - Version Web LaTeX | WikiPrépa | WikiPrépa