J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

Mines Physique 1 MP 2003

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo mines
🔗 Explorer
Banque
Mines
Année
2003
Filière
MP
Matière
Physique
Mines MPMines 2003MP PhysiquePhysique 2003
2025_09_04_74d9e7b799f78bdc0cdbg

ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURS DE L'AÉRONAUTIQUE ET DE L'ESPACE DE TECHNIQUES AVANCÉES, DES TÉLECOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE ÉCOLE POLYTECHNIQUE (FILIERE TSI) CONCOURS D'ADMISSION PREMIÈRE ÉPREUVE DE PHYSIQUE

Filière MP(Durée de l'épreuve : heures; l'usage de la calculatrice est autorisé)Sujet mis à disposition des concours : Cycle international, ENSTIM, INT, TPEEIVP

Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
Physique I - Filière MP
L'énoncé de cette épreuve, particulière aux candidats de la filière MP, comporte 6 pages.
  • Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
  • Il ne faudra pas hésiter à formuler tout commentaire qui vous semblera pertinent, même lorsque l'énoncé ne le demande pas explicitement. Le barème tiendra compte de ces initiatives ainsi que des qualités de rédaction de la copie.

La surface de la Lune

On se propose d'étudier deux aspects de la surface lunaire : la température de surface et le sol. Ces deux parties sont indépendantes entre elles.
Dans tout le problème, étoile et planètes seront considérées comme des sphères en équilibre thermique, et qui se comportent comme des corps noirs.
  • Important : on trouvera en pages 5 et 6 un ensemble de données relatives à ce problème; ces données complètent (ou, à l'occasion, répètent) celles de l'énoncé. Quelquesunes de ces données pourront servir plusieurs fois ; d'autres n'ont de valeur qu'informative. Quand l'énoncé ne les indique pas, il appartient aux candidats de repérer et d'utiliser les données utiles pour la résolution de certaines questions.
  • Les questions numérotées avec un astérisque (par exemple, *) sont de type essentiellement qualitatif ; elles demandent peu de calculs, voire pas du tout.

Partie I Températures de surface

Température terrestre

  • Un modèle bien fruste
  • 1 - On modélise la surface de la Terre par une coquille sphérique de température uniforme, en équilibre thermodynamique : puissance absorbée et puissance émise sont égales. Soit la puissance totale émise par le Soleil. Exprimer en fonction du rayon solaire et
    de la température solaire . Exprimer, en fonction de , la puissance reçue par la Terre, à la distance du Soleil, supposé ponctuel. Exprimer alors la température de surface de la Terre, .
    - En réalité, la puissance absorbée par la surface de la Terre n'est qu'une fraction de la puissance du rayonnement solaire incident : la surface terrestre réfléchit la fraction , nommée albédo, de ce rayonnement. L'albédo moyen de la Terre est égal à 0,35 , ce qui signifie que 65 % du rayonnement solaire incident est absorbé. Établir l'expression suivante de la température de surface de la Terre :
- Calculer alors la valeur numérique de ; ne pas s’offusquer de la valeur trouvée à partir de ce premier modèle.

- Influence de l'atmosphère terrestre

L'atmosphère joue un rôle essentiel dans le bilan thermique terrestre. Désormais, on entendra par « Terre» la planète proprement dite, de rayon , entourée d'une pellicule sphérique de gaz, qui constitue l'atmosphère.
L'atmosphère est modélisée par une couche d'épaisseur et de température uniforme ; elle absorbe la fraction du rayonnement solaire non réfléchi ; elle absorbe aussi la totalité du rayonnement du corps noir émis par la surface de la Terre. La Terre absorbe la totalité du rayonnement émis par l'atmosphère vers celle-ci (Fig. 1).
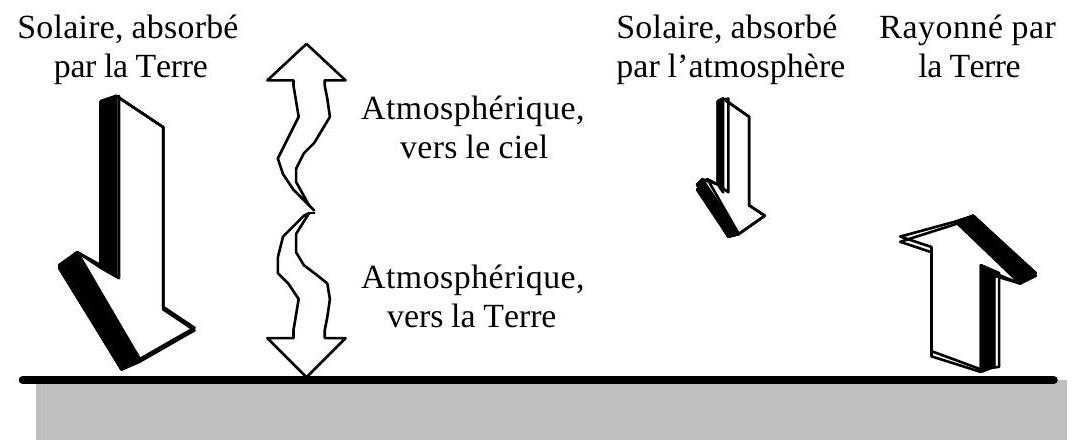
Fig. 1 : un bilan des rayonnements
4* - À quoi pourrait être due la différence d'absorption de l'atmosphère pour les rayonnements solaire et terrestre?
- Soit la température superficielle moyenne de la Terre calculée en tenant compte de l'influence de l'atmosphère. Exprimer , puissance solaire absorbée par la surface terrestre ; exprimer , puissance rayonnée par l'atmosphère vers la Terre. Effectuer un bilan thermique pour l'atmosphère. En déduire la relation .
- Application numérique : calculer pour (l'égalité est fortuite).
- Montrer que la température de l'atmosphère, , est égale à .

Température lunaire

- Température de la surface ensoleillée

L'albédo moyen de la Lune, , est égal à du flux solaire est absorbé par le sol. On suppose l'albédo uniforme sur toute la surface éclairée.
- Exprimer et calculer la valeur numérique de la température de surface de la Lune, , en ne tenant compte que du rayonnement solaire.
  • 9* - L'hypothèse d'une température uniforme pour la Lune n'est pas conforme à la réalité : la surface lunaire présente de gros écarts de température. Représenter sur un schéma la position, par rapport au Soleil, de la zone de températures les plus élevées.
    - Effectuer un bilan thermique pour une surface élémentaire de cette zone et en déduire , la température maximale à la surface de la Lune. La valeur expérimentale est de l'ordre de .
  • Le «clair de Terre».
Lorsque l'axe Soleil-Lune est perpendiculaire à l'axe Lune-Terre, on cherche à déterminer la température superficielle de la Lune en un point éclairé uniquement par la Terre. Ce point reçoit le rayonnement de deux corps noirs de nature différente, celui du Soleil, réfléchi par la Terre, et celui de l'atmosphère terrestre.
- Évaluer la puissance surfacique de chacun de ces rayonnements.
- Déterminer la température maximale à la surface de la Lune uniquement éclairée par la Terre : .
13* - Comment serait modifiée la température d'un point M' situé dans la zone éclairée par le Soleil si l'on tenait compte également du rayonnement terrestre?
14* - Un instrument situé à la surface de la Lune détecte un rayonnement visible et un rayonnement infrarouge. Indiquer le domaine de longueurs d'onde caractéristique de chacun de ces rayonnements. Le résultat sera donné en micromètres.
15* - À quel domaine de longueurs d'onde appartient le rayonnement thermique émis par la Lune ? quelle est l'origine du rayonnement visible provenant de la Lune ?
  • Influence de la radioactivité
La Lune contient des roches radioactives, essentiellement et . La puissance volumique moyenne libérée par les roches lunaires, , a été évaluée à .
16 - Exprimer la température superficielle de la Lune, , pour les zones à l'ombre du Soleil et de la Terre et en ne tenant compte que de l'apport énergétique radioactif.
17* - La radioactivité modifie-t-elle de façon significative la température dans les zones très éclairées ?

Partie II Le sol lunaire

Modélisations

Le sol lunaire est bombardé et réduit en poussière par les météorites et le vent solaire, constitué essentiellement de protons et d'électrons. La composition du sol lunaire est proche de celle des silicates, dont quelques caractéristiques physiques sont indiquées pages 5 et 6 . La couche supérieure, très fine, est représentée par un empilement compact de sphères de
silicates, de rayon et de température uniforme (Fig. 2). Le contact entre les sphères est supposé ponctuel. On note la distance verticale minimale entre deux sphères en positions semblables : . Dans une telle structure compacte, le volume occupé par les sphères est de l'ordre de 74 % du volume de l'empilement.
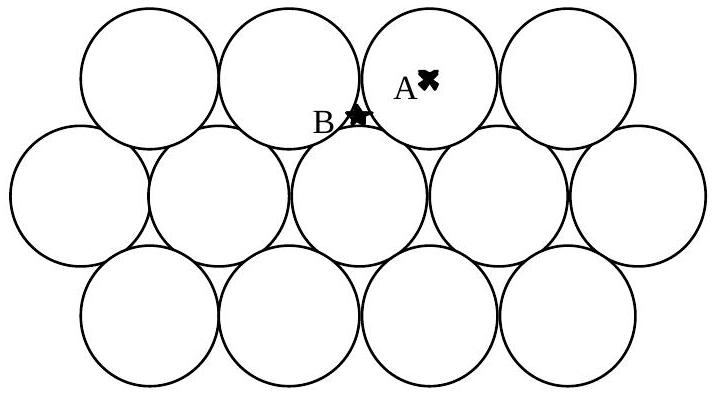
Fig. 2 : Le plan inférieur de l'empilement compact est constitué de sphères dont les centres sont notés . Une couche identique de sphères, dont les centres sont à l'à-pic des points de type B, est superposée à ce plan. Les centres des sphères de la troisième couche sont en sites de type , et ainsi de suite (empilement de type ).
18* - Justifier qu'avec un tel modèle les échanges thermiques entre les sphères soient limités au rayonnement.
19* - L’empilement précédent est maintenant modélisé par un ensemble de plans parallèles opaques, placés dans le vide, séparés par la distance . Que pensezvous de ce modèle ?
- On suppose que l'écart de température d'un plan à l'autre est très petit devant la température de ces plans. La puissance surfacique émise à l'équilibre thermodynamique par un corps de température est , où est la constante de Stefan. Exprimer à l'aide de ces hypothèses le flux thermique qui se propage de plan en plan dans la direction perpendiculaire à ces derniers. Montrer que l’on peut caractériser le milieu ainsi modélisé par un coefficient de conductivité thermique dépendant de la température de la forme ; trouver la valeur de et l'expression de .
- La dimension des grains de poussière est, en ordre de grandeur, ; comparer l'ordre de grandeur de obtenu avec ce modèle avec la valeur expérimentale de la conductivité des silicates : .
- Comparer la densité et la capacité calorifique massique de la couche supérieure avec et .
23* - Il est généralement admis que ce sont les couches les plus profondes qui ont les caractéristiques physiques les plus voisines de celles des modèles ci-dessus. Pourquoi ?

Influence de l'impact des météorites

On admet que les météorites heurtant la surface lunaire ont même composition que le sol lunaire. On rappelle que le référentiel de Copernic, ou référentiel héliocentrique, est lié au centre de masse du système solaire et que ses axes pointent vers des étoiles réputées fixes. Le référentiel de Copernic est supposé galiléen.
  • 24 - Vérifier que la vitesse d'impact d'une météorite frappant la surface lunaire et de vitesse négligeable dans le référentiel de Copernic est de l’ordre de .
  • 25 - Montrer que l'impact d'une météorite de masse peut dégager une énergie suffisante pour porter à l'état liquide une masse de la surface de la Lune. Déterminer puis calculer le rapport .
    - La solidification du matériau en fusion n'est pas sans effet sur la nature des transferts thermiques ultérieurs. Vers quelle valeur se rapproche alors la conductivité thermique calculée précédemment?

Fin de l'énoncé
Fin du problème

Données numériques (avec une précision variable)

Soleil

  • Rayon
  • Température de surface
  • L'angle solide sous lequel on voit la Terre depuis le Soleil est

Terre

  • Rayon terrestre
  • Distance Terre-Soleil
  • Masse terrestre
  • Albédo

Lune

  • Rayon lunaire
  • Masse lunaire
  • Distance Terre-Lune
  • Période du mouvement circulaire autour de la Terre jours (en restant dans le plan de l'orbite terrestre)
  • Période de rotation propre de la Lune jours . La Lune présente ainsi toujours la même face à la Terre.

Silicates

  • Densité
  • Conductivité thermique
  • Capacité calorifique massique
  • Ordre de grandeur du rayon
  • Température de fusion du silicate
  • Chaleur latente de fusion

Constantes physiques

  • Célérité de la lumière dans le vide
  • Constante de la gravitation
  • Constante de Planck
  • Constante de Boltzmann
  • Charge électrique élémentaire
  • Masse de l'électron
  • Constante de Stefan
  • Nombre d'Avogadro
  • Permittivité du vide F.
  • Constante des gaz parfaits

Données physiques

Loi de rayonnement du corps noir (loi de Planck)

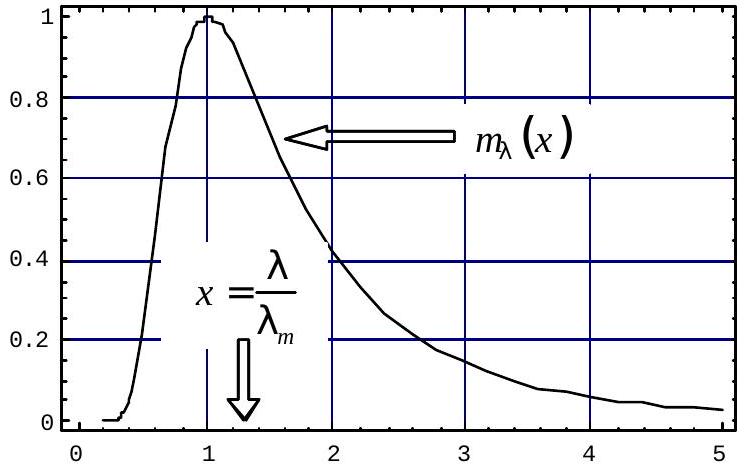
L'exitance (en W. ) d'une source est la puissance totale qu’elle émet par unité de surface, toutes directions et toutes longueurs d'onde confondues.
La loi de Stefan stipule que l'exitance d'un corps noir augmente comme la quatrième puissance de sa température : .
L'exitance spectrale est la puissance émise à la température par l'unité de surface du corps noir dans l'intervalle spectral .
Son expression est . L'exitance spectrale est maximale pour la longueur d'onde liée à la température par la relation . On a donc . Posons ; la figure ci-dessus représente la fonction .

Formule mathématique

.
Mines Physique 1 MP 2003 - Version Web LaTeX | WikiPrépa | WikiPrépa