Version interactive avec LaTeX compilé

Mines Option Informatique MP 2012

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

Mines MP Mines 2012 MP Info Info 2012

2025_08_29_0d3bfd2ef7dc20a224c9g

ECOLE DES PONTS PARISTECH, SUPAERO (ISAE), ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH, MINES DE SAINT-ETIENNE, MINES DE NANCY, TELECOM BRETAGNE, ENSAE PARISTECH (FILIERE MP) ECOLE POLYTECHNIQUE (FILIERE TSI)

CONCOURS 2012
EPREUVE d'INFORMATIQUE
Filière : MP
Durée de l'épreuve : 3 heures. L'utilisation d'une calculatrice est autorisée.

Sujet mis à la disposition des concours : Cycle International, ecoles des Mines, TELECOM SudParis, TPE-EIVP.

L'énoncé de cette épreuve comporte 14 pages.

Les candidats sont priés de mentionner de façon apparente
sur la première page de la copie :
INFORMATIQUE - MP

Recommandations aux candidats

Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Tout résultat fourni dans l'énoncé peut être utilisé pour les questions ultérieures même s’il n’a pas été démontré.
Il ne faut pas hésiter à formuler les commentaires qui semblent pertinents même lorsque l'énoncé ne le demande pas explicitement.

Composition de l'épreuve

L'épreuve comporte :

un exercice sur les langages rationnels : page 2
un problème d'algorithmique et programmation : pages 3 à 14

Exercice sur les langages rationnels

Un alphabet

est un ensemble fini non vide d'éléments appelés lettres. Un mot sur

est une suite finie de lettres de

; la longueur d'un mot

est le nombre de lettres composant

; le mot de longueur nulle est noté

. On désigne par

l'ensemble des mots sur

, y compris le mot

. Un langage sur

est une partie de

On dit qu'un mot

sur

, de longueur non nulle, est un facteur d'un mot

sur

s'il existe deux mots

sur

avec

; si

est le mot de longueur nulle, on dit que

est un préfixe de

; si

est le mot de longueur nulle, on dit que

est un suffixe de

Un mot peut posséder plusieurs occurrences d'un même facteur

. Supposons que l'on ait

. Le mot baabaabbaabaaa contient deux occurrences disjointes du facteur

, de même que le mot aabaaaabaaa. Le mot abaabaaabaabb contient deux occurrences non disjointes du facteur

, de même que le mot aabaabaa ; dans ce dernier cas, la première occurrence de

est un préfixe du mot aabaabaa alors que la seconde occurrence en est un suffixe.

Dans tout l'exercice,

désigne un alphabet et

désigne un mot de longueur non nulle sur

1 - Montrer que le langage

sur

des mots qui contiennent au moins une occurrence du facteur

est rationnel.
2 - Montrer que le langage

sur

des mots qui contiennent au moins deux occurrences disjointes du facteur

est rationnel.
3 - Montrer que le langage

sur

des mots qui contiennent au moins deux occurrences non disjointes du facteur

est rationnel.
4 - Montrer que le langage

sur

des mots qui contiennent exactement une occurrence du facteur

est rationnel.

Problème d'algorithmique et programmation

Préliminaire concernant la programmation

Il faudra écrire des fonctions ou des procédures à l'aide d'un langage de programmation qui pourra être soit Caml, soit Pascal, tout autre langage étant exclu. Indiquer en début d'épreuve le langage de programmation choisi; il est interdit de modifier ce choix au cours de l'épreuve. Certaines questions du problème sont formulées différemment selon le langage de programmation ; cela est indiqué chaque fois que cela est nécessaire. Lorsque le candidat écrira une fonction ou une procédure, il pourra faire appel à une autre fonction ou procédure définie dans les questions précédentes. Enfin, si les paramètres d'une fonction ou d'une procédure à écrire sont supposés vérifier certaines hypothèses, il ne sera pas utile dans l'écriture de cette fonction ou de cette procédure de tester si les hypothèses sont bien vérifiées.
Dans les énoncés du problème, un même identificateur écrit dans deux polices de caractères différentes désignera la même entité, mais du point de vue mathématique pour la police en italique (par exemple

) et du point de vue informatique pour celle en romain (par exemple n ).

Un graphe

est défini par deux ensembles

. L'ensemble

est un ensemble fini d'éléments appelés sommets. L'ensemble

est un ensemble de paires de sommets. Un élément

est appelé arête de

sont les extrémités de l'arête. L'ordre d'un graphe

est le nombre de sommets de

. Un graphe est représenté par un dessin où des cercles représentent les sommets et un trait joignant deux cercles représente une arête composée des deux sommets correspondant aux cercles. Si

est une arête de

, on dit que

sont voisins. Le degré d'un sommet

est le nombre de voisins de

.
On dit que deux arêtes d'un graphe

sont incidentes si elles ont une extrémité en commun. On appelle couplage dans

un ensemble d'arêtes de

deux à deux non incidentes.
Un graphe

est dit biparti si on peut partitionner son ensemble de sommets

en deux sous-ensembles

de sorte que toute arête ait une extrémité dans

et une extrémité dans

. Si les ensembles

ont même cardinal, on dit qu'il s'agit d'un graphe biparti équilibré. Dans tout le problème, on ne considère que des graphes bipartis équilibrés. On note

le cardinal commun aux ensembles

; l'ordre du graphe est donc égal à

. On suppose que l'on a toujours

. Les sommets de

sont numérotés de 0 à

et nommés

; les sommets de

sont numérotés de 0 à

et nommés

. Une arête de

est toujours écrite en mettant d'abord l'extrémité qui est dans

puis celle qui est dans

On représente les graphes bipartis équilibrés par des schémas comme on peut le voir dans la figure 1 avec le graphe

, en représentant les sommets de

à gauche et les sommets de

à droite.

Pour

vaut 4 et l'ordre de

vaut 8 . Les arêtes de

sont:

.
Le sommet

est de degré 3 .
Le sommet

est de degré 1 .
Le sommet

est de degré 4 .
Le sommet

est de degré 1 .
Les sommets

sont de degré 2 .
Le sommet

est de degré 3 .

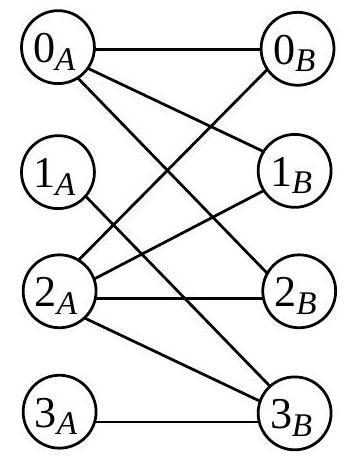
Figure 1 : le graphe

Dans le graphe

, les arêtes

étant non incidentes, elles forment un couplage, nommé

, dont les arêtes sont dessinées en gras ci-contre ; on dit alors que dans ce couplage :

le sommet est couplé au sommet , et réciproquement ;
le sommet est couplé au sommet , et réciproquement ;
les sommets et sont non couplés.

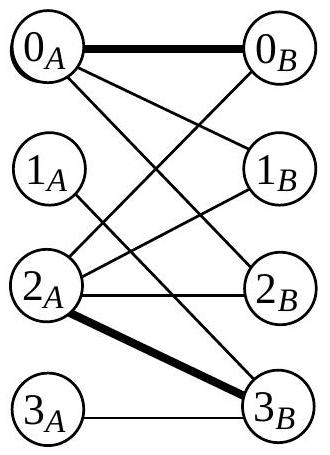
Figure 2 : le graphe

et le couplage

Le cardinal d'un couplage est le nombre d'arêtes de celui-ci ; par exemple le cardinal de

vaut 2.

Première partie : généralités

5 - Exhiber un couplage de cardinal 3 dans

.
6 - Indiquer s'il existe dans

un couplage de cardinal 4. Justifier la réponse.
Un graphe biparti équilibré d’ordre

est représenté par une matrice carrée de dimension

dont les lignes correspondent aux éléments de

et les colonnes aux éléments de

. Les cases de cette matrice sont indicées par (

) avec

et contiennent des valeurs booléennes: la case d'indice (

) contient la valeur «vrai» (ou true dans le langage de programmation) si

est une arête du graphe ; elle contient la valeur «faux» (ou false dans le langage de programmation) dans le cas contraire. Le graphe

ci-dessus est donc représenté par la matrice suivante :

	0	1	2	3
0	vrai	vrai	vrai	faux
1	faux	faux	faux	vrai
2	vrai	vrai	vrai	vrai
3	faux	faux	faux	vrai

Figure 3 : la matrice représentant

Un couplage est représenté par un tableau d'entiers indicé de 0 à

. Soit

vérifiant

; si le sommet

est couplé avec le sommet

, la case d'indice

contient la valeur

; si le sommet

n'est pas couplé, la case d'indice

contient une valeur égale à -1 . Le couplage

, formé des arêtes

, est représenté par le tableau cidessous :

	0	1	2	3
	0	-1	3	-1

Figure 4 : le tableau représentant

Indications pour la programmation

Caml : Un vecteur est par la suite nommé aussi tableau.
On nomme matrice un tableau à deux dimensions (un vecteur de vecteurs).
La matrice représentant un graphe biparti équilibré d'ordre

est codée en Caml par une matrice

de booléens. La matrice représentant

est ainsi codée par :

let G0 = [|[|true; true; true; false|];
    [|false; false; false; true|];
    [|true; true; true; true|];
    [|false; false; false; true|];|];;

Un couplage est codé par un vecteur de

entiers ; le couplage

est ainsi codé par :

let C0 = [|0; -1; 3; -1|];;

Une arête

est codée par un vecteur a de deux entiers, avec a . (0) dans

et a . (1) dans

Fin des indications pour Caml

Pascal : on utilise les définitions suivantes :

const MAX = 100;

type Matrice

of Boolean;
type Tableau = array[0 .. MAX - 1] of Integer;
type Arete = array[0 .. 1] of Integer;

La constante MAX donne une borne supérieure du cardinal des parties

des graphes bipartis équilibrés considérés, c'est-à-dire de la moitié de l'ordre du graphe ; il ne sera pas utile de vérifier cette condition dans la programmation.
Le type Matrice sert à coder les graphes bipartis équilibrés. La matrice représentant le graphe

est ainsi codée par G0 de type Matrice avec :

G0[0,0]:= true; G0[0,1]:= true; G0[0,2]:= true; G0[0,3]:= false;
G0[1,0]:= false; G0[1,1]:= false; G0[1,2]:= false; G0[1,3]:= true;
G0[2,0]:= true; G0[2,1]:= true; G0[2,2]:= true; G0[2,3]:= true;
G0[3,0]:= false; G0[3,1]:= false; G0[3,2]:= false; G0[3,3]:= true;

Le type Tableau a plusieurs usages. Il sert entre autres à coder un couplage ; le couplage

est ainsi codé par C0 de type Tableau avec :
C0[0] := 0; C0[1] := -1; C0[2] := 3; C0[3] := -1;
Une arête

est codée par un tableau a de type Arete, avec

dans

.
Fin des indications pour Pascal

7 - Soit

un graphe biparti équilibré d'ordre

. On considère un tableau

d'entiers de longueur

et contenant dans ses cases indicées de 0 à

soit la valeur -1 , soit une valeur comprise entre 0 et

. Il s'agit de savoir si ce tableau

représente ou non un couplage dans

.
Caml : Écrire en Caml une fonction verifie telle que,

si G est une matrice codant le graphe ,
si C est un vecteur codant le tableau ,
alors verifie G C renvoie true si le tableau représente un couplage dans et false sinon.
Indiquer la complexité de la fonction verifie.
Pascal : Écrire en Pascal une fonction verifie telle que,
si G , de type Matrice, code le graphe ,
si C, de type Tableau, code le tableau C,
si n , de type Integer, contient la valeur de ,
alors verifie(G, C, n) renvoie true si le tableau représente un couplage dans et false sinon.
Indiquer la complexité de la fonction verifie.
- On considère un tableau , de longueur , codant un couplage d'un graphe . Il s'agit d'écrire une fonction qui calcule le cardinal de ce couplage.
Caml : Écrire en Caml une fonction cardinal telle que, si C est un vecteur codant un couplage, alors cardinal C renvoie le cardinal de ce couplage.
Indiquer la complexité de la fonction cardinal.
Pascal : Écrire en Pascal une fonction cardinal telle que,
si C, de type Tableau, code un couplage C,
si n , de type Integer, contient la valeur de , alors cardinal( ) renvoie le cardinal de . Indiquer la complexité de la fonction cardinal.

Deuxième partie : un algorithme pour déterminer un couplage maximal

On dit qu'un couplage

dans un graphe

est maximal si toute arête de

n'appartenant pas à

est incidente à au moins une arête de

. Par exemple, le couplage

est maximal. Un couplage maximal de

n'est pas forcément de cardinal maximum parmi les couplages de

. On cherche à concevoir un algorithme qui détermine un couplage maximal dans un graphe biparti équilibré

L'algorithme, nommé algo_approche, est le suivant :

on commence avec un couplage vide ;
tant que possède au moins une arête :
on choisit une arête de dont la somme des degrés des extrémités soit minimum ;
on ajoute l'arête au couplage ;
on retire de l'arête et toutes les arêtes incidentes à .

On admettra que le résultat est, par construction, un couplage maximal.
9 - Appliquer algo_approche au graphe

(voir la figure 1 page 4).
On considère par la suite le graphe biparti équilibré

d’ordre 12 représenté sur la figure 5.

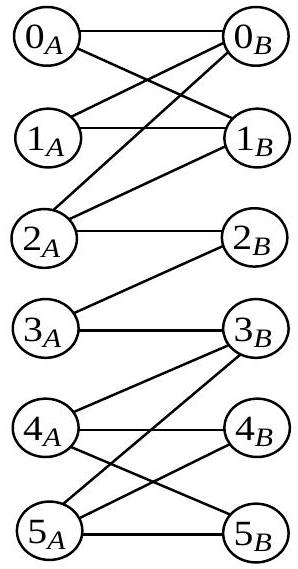
Figure 5 : le graphe

10 - On applique algo_approche au graphe

. Déterminer la première arête

choisie par algo_approche; tracer le graphe obtenu après suppression de

et des arêtes incidentes à

. Montrer que le couplage obtenu par algo_approche est de cardinal au plus 5 et indiquer s'il est de cardinal maximum parmi les couplages de

.
11 - Soit

un graphe biparti équilibré d'ordre

. Il s'agit d'écrire en langage de programmation une fonction arete_min qui détermine une arête de

dont la somme des degrés des extrémités soit minimum. Si le graphe possède au moins une arête, cette fonction modifie un tableau

de deux entiers reçu en paramètre pour mettre dans les deux cases de a les numéros des deux extrémités d'une arête qui atteint ce minimum ; dans ce cas, la fonction renvoie la valeur «vrai» (true) ; sinon, elle renvoie la valeur «faux» (false).
Caml : Écrire en Caml une fonction arete_min telle que :

si G est une matrice codant le graphe ,
si a est un vecteur de deux entiers,
alors arete_min G a effectue les opérations décrites ci-dessus, en modifiant le tableau a dans le cas où possède au moins une arête.
Indiquer la complexité de la fonction arete_min.

Pascal : Écrire en Pascal une fonction arete_min telle que :

si G , de type Matrice, code le graphe ,
si n , de type Integer, contient la valeur de ,
si a est de type Arete,
alors arete_min(G, n, a) effectue les opérations décrites ci-dessus en modifiant le tableau a dans le cas où possède au moins une arête.
Indiquer la complexité de la fonction arete_min.
12 - Il s'agit d'écrire en langage de programmation une fonction ou une procédure supprimer qui supprime d'un graphe biparti équilibré une arête donnée et toutes les arêtes incidentes à .
Caml : Écrire en Caml une fonction supprimer telle que :
si G est une matrice codant un graphe biparti équilibré ,
si a est un vecteur de deux entiers codant une arête de , alors supprimer G a modifie G pour que, après modifications, G code le graphe obtenu à partir de en supprimant et toutes les arêtes incidentes à .
Indiquer la complexité de la fonction supprimer.
Pascal : Écrire en Pascal une procédure supprimer telle que :
si G , de type Matrice, code un graphe biparti équilibré d'ordre ,
si n , de type Integer, contient la valeur de ,
si a, de type Arete, code une arête de , alors supprimer , a modifie G pour que, après l'appel à la procédure, G code le graphe obtenu à partir de en supprimant et toutes les arêtes incidentes à . Indiquer la complexité de la procédure supprimer.

13 - Il s'agit de définir en langage de programmation l'algorithme algo_approche décrit au début de la deuxième partie.
Caml : Écrire en Caml une fonction algo_approche telle que, si G est une matrice qui code un graphe biparti équilibré

, algo_approche

effectue algo_approche à partir d'une copie de G et renvoie un vecteur codant le couplage obtenu.
Indication : on pourra utiliser sans la définir une fonction dupliquer_matrice telle que, si G est une matrice codant un graphe biparti équilibré

, dupliquer_matrice G renvoie une matrice identique à G . Cette fonction sera utilisée pour que la fonction algo_approche ne modifie pas le contenu de la matrice reçue en paramètre.
Indiquer la complexité de la fonction algo_approche.
Pascal : Écrire en Pascal une fonction algo_approche telle que :

si G , de type Matrice, code un graphe biparti équilibré d'ordre ,
si n , de type Integer, contient la valeur de , alors algo_approche( ) effectue algo_approche et renvoie un tableau de type Tableau codant le couplage obtenu. On fera en sorte que la fonction ne modifie pas la matrice G .
Indiquer la complexité de la fonction algo_approche.

Troisième partie : recherche exhaustive d'un couplage de cardinal maximum

- Soit

un graphe biparti équilibré d'ordre

. Il s'agit d'écrire en langage de programmation une fonction nommée une_arete qui recherche une arête quelconque de

. Si

possède au moins une arête, la fonction mémorise la première arête rencontrée

dans un tableau (ou vecteur en Caml) de deux entiers reçu en paramètre ; elle arrête alors sa recherche et renvoie la valeur «vrai» (true) ; sinon, la fonction renvoie la valeur «faux» (false).
Caml : Écrire en Caml une fonction une_arete telle que :

si G est une matrice codant le graphe ,
si a est un vecteur de deux entiers destiné à coder l'arête , alors une_arete G a effectue les opérations décrites ci-dessus, en modifiant le vecteur a dans le cas où possède au moins une arête.

Pascal : Écrire en Pascal une fonction une_arete telle que :

si G , de type Matrice, code le graphe ,
si n , de type Integer, contient la valeur de ,
si a, de type Arete, est destiné à coder l'arête , alors une_arete(G, n, a) effectue les opérations décrites ci-dessus en modifiant le tableau a dans le cas où possède au moins une arête.

15 - On cherche à établir un algorithme récursif, nommé meilleur_couplage, qui permette de déterminer un couplage de cardinal maximum dans un graphe biparti équilibré. Le principe est le suivant.
Si le graphe courant ne contient aucune arête, le cardinal maximum d'un couplage est 0 et aucun sommet n'est couplé.
Dans le cas contraire, l'algorithme considère une arête quelconque

du graphe courant et recherche successivement :

un couplage de cardinal maximum parmi les couplages du graphe courant ne contenant pas a
un couplage de cardinal maximum parmi les couplages du graphe courant contenant .
L'algorithme déduit alors un couplage de cardinal maximum.
Caml : Écrire en Caml une fonction récursive meilleur_couplage telle que, si G est une matrice codant un graphe biparti équilibré , meilleur_couplage G renvoie un vecteur codant un couplage de cardinal maximum dans . La fonction utilisera le principe décrit plus haut.
Indication : on pourra utiliser sans la définir une fonction dupliquer_matrice telle que, si G est une matrice codant un graphe biparti équilibré , alors dupliquer_matrice G renvoie une matrice identique à G .

Pascal : Écrire en Pascal une fonction récursive meilleur_couplage telle que :

si G , de type Matrice, code un graphe biparti équilibré d'ordre ,
si n , de type Integer, contient la valeur de , alors meilleur_couplage( ) renvoie un tableau de type Tableau codant un couplage de cardinal maximum dans . La fonction utilisera le principe décrit plus haut.

Quatrième partie : l'algorithme hongrois

On considère un graphe biparti équilibré

et un couplage

. Une chaîne de

est une suite

de sommets distincts telle que, pour

compris entre 0 et

est une arête de

. Le sommet

s'appelle l'origine de la chaîne et le sommet

l'extrémité de la chaîne.

Une chaîne

, avec

, est dite alternée relativement à

si :

pour tout indice pair, est dans ,
pour tout indice impair, est dans ,
le sommet n'est pas couplé,
pour tout entier vérifiant , l'arête n'appartient pas à ,
pour tout entier vérifiant , l'arête appartient à .

Autrement dit :

l'origine de la chaîne est dans et n'est pas couplée,
la première arête de la chaîne n'est pas dans , la deuxième est dans , la troisième n'est pas dans et ainsi de suite.

Une chaîne

alternée relativement au couplage

est dite chaîne alternée augmentante relativement à

si on a

et si de plus

n'est pas couplé, ce qui entraîne que

est dans

. Par exemple, dire qu'une chaîne

constitue une chaîne alternée augmentante relativement à un couplage

signifie que :

et sont des sommets de et sont des sommets de ;
sont des arêtes de ;
'est pas couplé dans 'est pas couplé dans ;
est couplé avec n'est pas couplé avec et est couplé avec .
- On considère le graphe et le couplage constitué des arêtes , représentées sur la figure 6 en gras. Après avoir indiqué le seul sommet de qui puisse être l'origine d'une chaîne alternée augmentante relativement à et le seul sommet de qui puisse être l'extrémité d'une chaîne alternée augmentante relativement à , déterminer une chaîne alternée augmentante

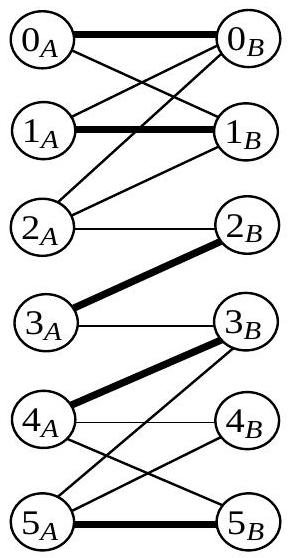
Figure 6 : le graphe

et le couplage

relativement à

17 - On considère un graphe biparti équilibré

et un couplage

dans

. Montrer que s'il existe une chaîne alternée augmentante relativement à

, alors il existe dans

un couplage dont le cardinal est égal au cardinal de

augmenté de 1 .

On admet le théorème suivant : un couplage C d'un graphe biparti équilibré G est de cardinal maximum si et seulement s'il n'existe pas dans

de chaîne alternée augmentante relativement à

Soit

un graphe biparti équilibré. L'algorithme hongrois s'appuie sur le théorème ci-dessus et détermine un couplage de cardinal maximum dans

. L'algorithme débute avec un couplage

de cardinal nul ; tant qu'il existe une chaîne augmentante relativement à

, l'algorithme modifie

pour incrémenter de 1 le cardinal du couplage en utilisant une telle chaîne augmentante.
La suite du problème a pour objectif de programmer cet algorithme. On commence par étudier la recherche d'une chaîne alternée augmentante.

On considère un graphe biparti équilibré

et un couplage

dans

. On va chercher s'il existe une chaîne alternée augmentante relativement à

. Pour cela, on recherche les sommets qui sont extrémités de chaînes alternées en procédant de proche en proche à partir des sommets de

non couplés.
Un sommet

est dit atteint si une chaîne alternée relativement à

et d'extrémité

est mise en évidence. Au départ, tous les sommets non couplés de

(un tel sommet est extrémité d'une chaîne alternée réduite à ce sommet) sont considérés comme atteints; aucun autre sommet n'est considéré comme atteint. Un sommet

non encore atteint peut être atteint à partir d'un de ses voisins

déjà atteint si on a:

soit est dans (et donc est dans ) et l'arête n'est pas dans le couplage ;
soit est dans (et donc est dans ) et l'arête est dans le couplage .

On utilise des marques attribuées aux sommets. Ces marques sont des entiers initialisés à -1 pour tous les sommets. Lorsqu'un sommet

est atteint à partir d'un sommet

, la marque de

devient égale au numéro de

(on rappelle que le numéro d'un sommet

ou d'un sommet

vaut

) ;

est alors l'avant-dernier sommet dans la chaîne alternée

d'extrémité

mise en évidence. La chaîne

peut être retrouvée à l'envers, de proche en proche, grâce aux marques ; dans cette chaîne, seule l'origine porte une marque de valeur -1 .
Si un sommet non couplé

est atteint,

est une chaîne alternée augmentante relativement à

.
Dans le cas où simultanément :

il n'y a plus de sommet non encore atteint qui puisse être atteint,
aucun sommet non couplé de n'est atteint, on admet qu'il n'existe pas de chaîne alternée augmentante relativement à .
Remarque: les valeurs des marques peuvent dépendre de l'ordre dans lequel on atteint les sommets, sans que cela n'ait d'importance pour la suite du problème.
- On considère le graphe et un couplage nommé constitué des arêtes , , en gras sur la figure 7 .
Certains sommets ont été atteints ; sur la figure 7, les marques attribuées sont portées à côté des sommets, les sommets atteints sont encadrés.
Utiliser les marques pour reconstituer la chaîne alternée arrivant dans le sommet et correspondant aux marques. Indiquer s'il s'agit d'une chaîne alternée augmentante relativement à .

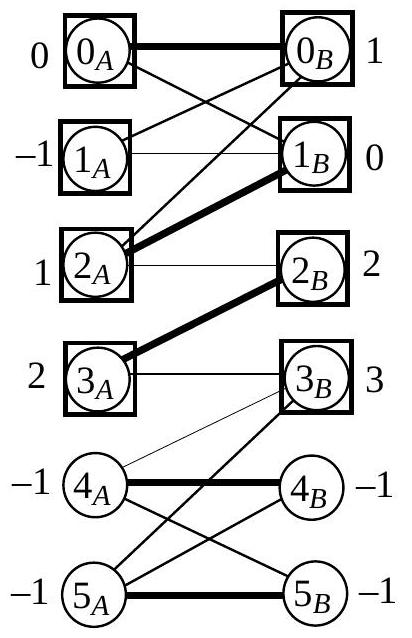
Figure 7 : le graphe

et le couplage

On considère quatre tableaux :

Un tableau nommé C codant un couplage .
Un tableau nommé R (pour réciproque) indicé par ; soit vérifiant ; si le sommet n'est pas couplé dans , la case d'indice du tableau R contient la valeur -1 ; si le sommet est couplé avec le sommet , la case d'indice du tableau comporte la valeur .
Un tableau nommé mA indicé par servant à contenir les marques des sommets de .
Un tableau nommé mB indicé par servant à contenir les marques des sommets de .
On suppose qu'une chaîne alternée augmentante relativement à un couplage a été déterminée et codée grâce aux marques. D’après la question , il existe un couplage de cardinal égal à celui de augmenté de 1 . La fonction ou procédure actualiser reçoit en paramètres les quatre tableaux décrits ci-dessus ainsi que le numéro de ; elle transforme alors les tableaux C et R pour qu'ils correspondent à un couplage, obtenu à partir de et de , dont le cardinal est celui du couplage augmenté de 1 .
Caml : Écrire en Caml une fonction actualiser telle que :
si sont des vecteurs de entiers qui correspondent à la description donnée plus haut,
si numero est un entier donnant le numéro de , alors actualiser CRmAmB numero modifie les vecteurs et pour obtenir un couplage de cardinal égal à celui de augmenté de 1 .

Pascal : Écrire en Pascal une procédure actualiser telle que :

si les tableaux , de type Tableau, correspondent à la description donnée plus haut,
si numero est un entier donnant le numéro de ,
alors actualiser( , numero) modifie les tableaux C et R pour obtenir un couplage de cardinal égal à celui de augmenté de 1 .

20 - On considère le graphe

ci-contre et un couplage, nommé

, constitué des arêtes

en gras sur la figure 8. Recopier la figure, encadrer tous les sommets qui peuvent être atteints et préciser à côté des sommets les marques obtenues. Indiquer s'il existe dans

une chaîne alternée augmentante relativement à

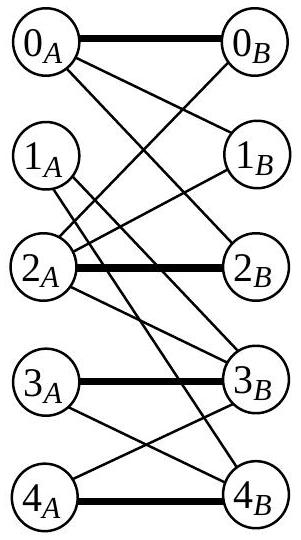
Figure 8 : le graphe

et le couplage

Indication : on procédera de proche en proche à partir du seul sommet non couplé de

, c'est-à-dire à partir du sommet

. L'ordre dans lequel on atteint les sommets n'a pas d'importance.

On suppose donnés un graphe biparti équilibré

et un couplage

dans

. Les chaînes alternées considérées dans la suite sont toujours des chaînes alternées relativement à

. Les questions

ont pour objectif de programmer un algorithme qui cherche une chaîne alternée augmentante en atteignant les sommets de proche en proche à partir des sommets non couplés de

- On suppose que certains sommets de

peuvent déjà avoir été atteints et les marques calculées en conséquence. On note

un sommet de

ou de

déjà atteint. On définit deux nouvelles fonctions, les fonctions chercherA et chercherB. Appliquée au sommet

, appelé sommet de départ, la fonction chercherA (si

est dans

) ou la fonction chercher

(si

est dans

) détermine des sommets non encore atteints qui peuvent être atteints, de voisin en voisin, récursivement, à partir de

, modifie les marques de ces sommets nouvellement atteints et s'arrête dans les cas suivants :

un sommet de non couplé a été atteint ; elle renvoie alors le numéro du sommet ;
tous les sommets qui peuvent être atteints de voisin en voisin à partir de l'ont été et aucun sommet non couplé de n'est atteint; elle renvoie alors la valeur -1 .
Il s'agit d'écrire les deux fonctions chercherA et chercherB en utilisant une récursivité croisée, chacune des deux fonctions pouvant faire appel à l'autre.
Caml : Définir ce qu’on appelle récursivité croisée et indiquer comment elle peut être implémentée en Caml.
Écrire en Caml les deux fonctions chercherA et chercherB ; chacune de ces deux fonctions reçoit en paramètres :
une matrice G codant le graphe ;
quatre vecteurs de longueur pour les quatre tableaux décrits plus haut : , mA et mB ;
un entier codant le numéro du sommet de départ de la recherche.

Ces deux fonctions modifient les vecteurs mA et mB conformément à la description cidessus. Elles renvoient le numéro d'un sommet atteint non couplé de

ou la valeur -1 selon le cas.

Pascal : Définir ce qu'on appelle récursivité croisée et indiquer comment elle peut être implémentée en Pascal.
Écrire en Pascal les deux fonctions chercherA et chercherB; chacune de ces deux fonctions reçoit en paramètres :

une matrice G , de type Matrice, codant le graphe ;
quatre tableaux de type Tableau pour les quatre tableaux décrits plus haut: et mB ;
un entier n contenant la valeur de donnant le cardinal commun à et ;
un entier codant le numéro du sommet de départ de la recherche.

Ces deux fonctions modifient les tableaux mA et mB conformément à la description cidessus. Elles renvoient le numéro d'un sommet atteint non couplé de

ou la valeur -1 selon le cas.

- On suppose donnés un graphe biparti équilibré

d'ordre

et un couplage

dans

. Tous les sommets de

possèdent une marque égale à -1 .
La fonction chaine_alternee cherche s'il existe une chaîne alternée augmentante en appliquant la fonction chercherA successivement à partir des sommets non couplés de

.
Caml : Écrire en Caml la fonction chaine_alternee telle que :

si G est une matrice codant le graphe ,
si et mB correspondent à la description donnée précédemment, toutes les cases de mA et mB étant initialisées à -1 , alors chaine_alternee G C R mA mB renvoie:
-1 s'il n'existe pas de chaîne alternée augmentante,
le numéro de l'extrémité d'une chaîne alternée augmentante dans le cas contraire.
De plus, la fonction modifie les vecteurs mA et mB pour qu'ils contiennent les marques des sommets à la fin de l'exécution de la fonction.

Pascal : Écrire en Pascal la fonction chaine_alternee telle que :

si G , de type Matrice, code le graphe ,
si et mB , de type Tableau, correspondent à la description donnée précédemment, les cases de mA et mB d'indices compris entre 0 et étant initialisées à -1 ,
si n , de type Integer, contient la valeur de , alors chaine_alternee( ) renvoie:
-1 s'il n'existe pas de chaîne alternée augmentante,
le numéro de l'extrémité d'une chaîne alternée augmentante dans le cas contraire.
De plus, la fonction modifie les tableaux mA et mB pour qu'ils contiennent les marques des sommets à la fin de l'exécution de la fonction.
- Dans cette question, on programme l'algorithme hongrois.
Caml : Écrire en Caml la fonction algorithme_hongrois telle que, si G est une matrice codant un graphe biparti équilibré , alors algorithme_hongrois G renvoie un vecteur codant le couplage obtenu par l'algorithme hongrois.

Pascal : Écrire en Pascal la fonction algorithme_hongrois telle que :

si G , de type Matrice, code un graphe biparti équilibré d'ordre ,
si n , de type Integer, contient la valeur de , alors algorithme_hongrois(G, n) renvoie un tableau de type Tableau codant le couplage obtenu par l'algorithme hongrois.