Version interactive avec LaTeX compilé
ÉCOLE NATIONALE DES PONTS ET CHAUSSÉES, ÉCOLES NATIONALES SUPÉRIEURES DE L'AÉRONAUTIQUE ET DE L'ESPACE, DE TECHNIQUES AVANCÉES, DES TÉLÉCOMMUNICATIONS, DES MINES DE PARIS, DES MINES DE SAINT-ÉTIENNE, DES MINES DE NANCY, DES TÉLÉCOMMUNICATIONS DE BRETAGNE, ÉCOLE POLYTECHNIQUE (FILIÈRE TSI)
CONCOURS D'ADMISSION 2009
ÉPREUVE D'INFORMATIQUE
ÉPREUVE D'INFORMATIQUE
Sujet mis à disposition des concours : ENSAE ParisTech, TELECOM SudParis (ex INT), TPE-EIVP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
INFORMATIQUE - MP
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
INFORMATIQUE - MP
L'énoncé de cette épreuve comporte 8 pages.
Recommandations aux candidats
- Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
- Tout résultat fourni dans l'énoncé peut être utilisé pour les questions ultérieures même s'il n'a pas été démontré.
- Il ne faut pas hésiter à formuler les commentaires qui semblent pertinents même lorsque l'énoncé ne le demande pas explicitement.
Composition de l'épreuve
L'épreuve comporte deux problèmes indépendants :
- un problème sur les automates, pages 2 et 3 ;
- un problème d'algorithmique, pages 4 à 8 .
Préliminaire pour l'ensemble de l'épreuve concernant la programmation
Il faudra écrire des fonctions ou des procédures à l'aide d'un langage de programmation qui pourra être soit Caml, soit Pascal, tout autre langage étant exclu. Indiquer en début d'épreuve le langage de programmation choisi; il est interdit de modifier ce choix au cours de l'épreuve. Certaines questions des problèmes sont formulées différemment selon le langage de programmation ; cela est indiqué chaque fois que cela est nécessaire. Lorsque le candidat écrira une fonction ou une procédure, il pourra faire appel à une autre fonction ou procédure définie dans les questions précédentes. Enfin, si les paramètres d'une fonction ou d'une procédure à écrire sont supposés vérifier certaines hypothèses, il ne sera pas utile dans l'écriture de cette fonction ou de cette procédure de tester si les hypothèses sont bien vérifiées.
Dans les énoncés des problèmes, un même identificateur écrit dans deux polices de caractères différentes désignera la même entité mais du point de vue mathématique pour une police (en italique ; par exemple
Problème 1. Automates
Les quelques rappels de définitions qui suivent permettent de fixer la terminologie et les notations.
Un alphabet
Un alphabet
Un automate fini
-
est un alphabet ; -
est un ensemble fini et non vide appelé ensemble des états de ; -
est appelé l'ensemble des transitions; étant donnée une transition , on dit qu'elle est d'origine , d'extrémité et qu'elle est d'étiquette ; on pourra la noter ; -
est appelé ensemble des états initiaux de ; -
est appelé ensemble des états finals de .
Dans ce problème, on considérera uniquement des automates ayant un seul état initial, noté
Un chemin de
Un chemin de
On rappelle le théorème de Kleene: un langage sur un alphabet
On ne considère dans tout ce problème que l'alphabet
On définit une application
-
; - si un mot
de longueur s'écrit où, pour appartient à , alors ; - si un mot
de longueur s'écrit où, pour , appartient à , alors .
La fonctionagit donc en échangeant chaque lettre d'indice pair avec la lettre (d'indice impair) qui la précède immédiatement. Ainsi, .
-Soit un mot dans . Établir une condition nécessaire et suffisante pour que, quel que soit le mot dans , l'égalité soit vérifiée.
On note
On note
On note
On se propose de montrer que si
Si
7 -Montrer que si
8 -On considère un automate fini
9 - On considère un automate fini
7 -Montrer que si
8 -On considère un automate fini
9 - On considère un automate fini
Soit
-
est un état utile ; -
n'est ni l'état initial, ni un état final ; - il n'existe dans
aucune transition dont l'origine et l'extrémité soient simultanément , c'est-à-dire aucune transition qui s'écrive quelle que soit l'étiquette considérée ; - il existe au moins deux transitions d'origine
ou au moins deux transitions d'extrémité .
On considère l'automate obtenu à partir de
10 -Soit
11 -Montrer que, si
Soit
12 -Montrer que si
13 -Soit
14 -Soit
15 -Soit
16 -Il s'agit d'écrire la fonction
Caml :
On utilise le type suivant pour représenter les lettres de l'alphabet
type lettre = a | b ;;
Un mot est codé par une liste de type lettre list ; par exemple, le mot
Écrire en Caml une fonction phi telle que, si un mot
Attention : l'emploi de références ou de vecteurs est interdit.
10 -Soit
11 -Montrer que, si
Soit
12 -Montrer que si
13 -Soit
14 -Soit
15 -Soit
16 -Il s'agit d'écrire la fonction
Caml :
On utilise le type suivant pour représenter les lettres de l'alphabet
type lettre = a | b ;;
Un mot est codé par une liste de type lettre list ; par exemple, le mot
Écrire en Caml une fonction phi telle que, si un mot
Attention : l'emploi de références ou de vecteurs est interdit.
Pascal :
On définit la constante et les types suivants :
const MAX = 100;
type Sigma = (a, b);
type Mot = array[1 .. MAX] of Sigma;
Écrire en Pascal une fonction phi telle que, si u de type Mot code un mot
const MAX = 100;
type Sigma = (a, b);
type Mot = array[1 .. MAX] of Sigma;
Écrire en Pascal une fonction phi telle que, si u de type Mot code un mot
Problème 2. Algorithmique
L'objectif de ce problème est de compter le nombre d'arbres enracinés, non ordonnés et étiquetés de nombre de nœuds donné. Pour cela, on étudie un codage particulier de ces arbres appelé codage de Prüfer.
Un arbre possède un nombre fini d'éléments appelés nœuds. Les arbres considérés dans ce problème possèdent tous au moins un nœud. Un arbre enraciné non ordonné
Un arbre est dit étiqueté si à chaque nœud est associé un entier positif ou nul, ces entiers étant deux à deux distincts; l'entier associé à un nœud est l'étiquette du nœud. On pourra nommer un nœud par son étiquette; si
Dans ce problème, le terme d'arbre désignera toujours un arbre enraciné non ordonné étiqueté.
Les deux dessins ci-dessous sont deux représentations graphiques d'un même arbre nommé
Les deux dessins ci-dessous sont deux représentations graphiques d'un même arbre nommé
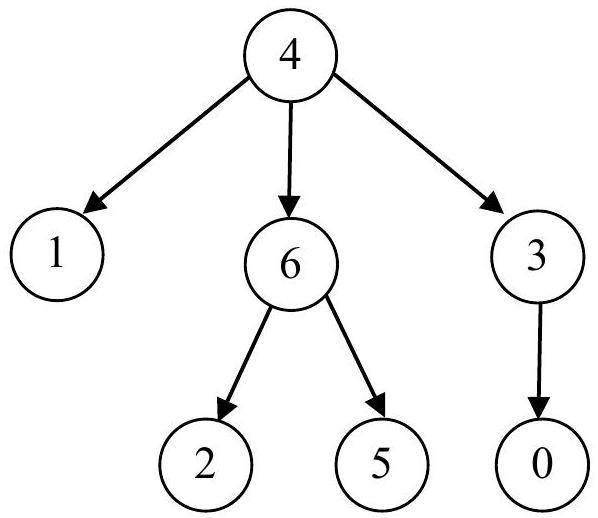
L'arbre
L'arbre
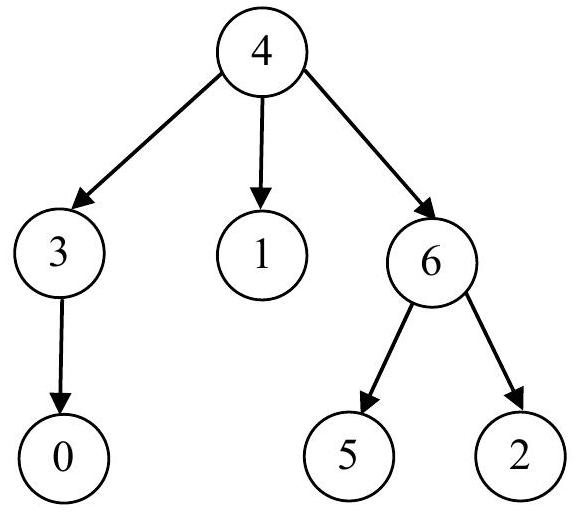
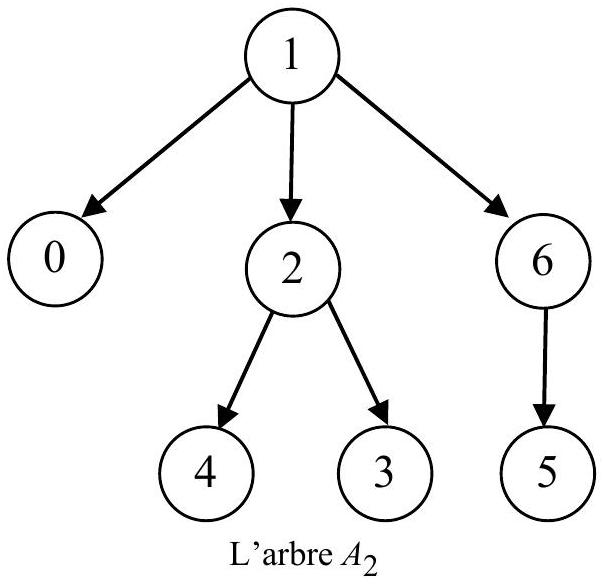
L'arbre
On dira qu'un arbre est un arbre étiqueté consécutivement s'il s'agit d'un arbre étiqueté et que l'ensemble de ses étiquettes forme un intervalle d'entiers de plus petite valeur 0 ; autrement dit, pour un arbre ayant
Première partie : d'un codage racine-fils-frères d'un arbre au codage de Prüfer
Soit
- l'étiquette de la racine (qui ne dépend pas de la représentation);
- un tableau nommé fils; pour
compris entre 0 et , la case d'indice du tableau fils contient la valeur -1 si le nœud est une feuille de l'arbre et, sinon, l'étiquette du fils du nœud se situant le plus à gauche dans la représentation graphique choisie ; - un tableau nommé freres; pour
compris entre 0 et , la case d'indice du tableau freres contient la valeur -1 si le nœud n'a aucun frère sur sa droite et, sinon, l'étiquette de son frère qui se trouve le premier sur sa droite.
Pour l'arbre
- la racine est le nœud 4 ;
- pour le tableau fils: les cases d'indices
et 5 contiennent la valeur -1 , la case d'indice 3 contient 0 , la case d'indice 4 contient 1 , la case d'indice 6 contient 2 ; - pour le tableau freres: les cases d'indices
et 5 contiennent la valeur -1 , la case d'indice 1 contient 6 , la case d'indice 2 contient 5 , la case d'indice 6 contient 3 .
Ainsi, l'arbre
| indice | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| fils | -1 | -1 | -1 | 0 | 1 | -1 | 2 |
| indice | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| freres | -1 | 6 | 5 | -1 | -1 | -1 | 3 |
On définit aussi deux tableaux qui peuvent être calculés à partir du codage racine-fils-frères :
- un tableau nommé peres ; pour
compris entre 0 et , la case d'indice contient la valeur -1 s'il s'agit de la racine de l'arbre et, dans les autres cas, l'étiquette du père du nœud ; pour l'arbre , la case d'indice 4 contient la valeur -1 , la case d'indice 0 contient 3 , les cases d'indices 1,3 et 6 contiennent 4 , les cases d'indices 2 et 5 contiennent la valeur 6 ; - un tableau nommé arites ; pour
compris entre 0 et , la case d'indice de ce tableau contient l'arité du nœud ; pour l'arbre , les cases d'indices et 5 contiennent la valeur 0 , la case d'indice 3 contient 1 , la case d'indice 4 contient 3 , la case d'indice 6 contient 2 .
Pour l'arbre, les tableaux peres et arites sont représentés ci-dessous :
| indice | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| peres | 3 | 4 | 6 | 4 | -1 | 6 | 4 |
| indice | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| arites | 0 | 0 | 0 | 1 | 3 | 0 | 2 |
Indications pour la programmation en Pascal
On définit la constante et le type suivant :
const MAX = 100;
type Tableau = array[0 .. MAX - 1] of Integer;
La constante MAX est un majorant du nombre de nœuds des arbres considérés.
const MAX = 100;
type Tableau = array[0 .. MAX - 1] of Integer;
La constante MAX est un majorant du nombre de nœuds des arbres considérés.
Fin des indications pour la programmation en Pascal
Caml : Écrire en Caml une fonction calculer_peres telle que, si on considère un arbre
- racine est un entier qui contient l'étiquette de la racine de
, - fils et freres sont deux vecteurs de longueur
qui représentent respectivement les tableaux fils et freres d'un codage racine-fils-frères de ,
alors calculer_peres racine fils freres renvoie un vecteur de longueurcorrespondant au tableau peres défini plus haut.
Pascal : Écrire en Pascal une fonction calculer_peres telle que, si on considère un arbre
- racine est un entier qui contient l'étiquette de la racine de
, - fils et freres sont de type Tableau et représentent respectivement les tableaux fils et freres d'un codage racine-fils-frères de
, - n est un entier qui contient le nombre de nœuds de
, alors calculer_peres(racine, fils, freres, n) renvoie un tableau de type Tableau contenant, entre les indices 0 et , le tableau peres défini plus haut.
-Indiquer, en fonction du nombre de nœuds de l'arbre considéré, la complexité de la fonction calculer_peres.
-Il s'agit d'écrire en langage de programmation une fonction nommée calculer_arites qui, à partir du codage racine-fils-frères d'un arbre étiqueté consécutivement, renvoie le tableau arites correspondant à cet arbre.
Caml : Écrire en Caml une fonction calculer_arites telle que, pour un arbrepossédant nœuds et étiqueté consécutivement, si fils et freres sont deux vecteurs de longueur qui représentent respectivement les tableaux fils et freres d'un codage racine-fils-frères de , alors calculer_arites fils freres renvoie un vecteur correspondant au tableau arites défini plus haut.
Pascal: Écrire en Pascal une fonction calculer_arites telle que, pour un arbre
- fils et freres sont de type Tableau et représentent respectivement les tableaux fils et freres d'un codage racine-fils-frères de
, - n est un entier qui contient le nombre de nœuds de
,
alors calculer_arites(fils, freres, n) renvoie un tableau de type Tableau contenant entre les indices 0 etles arités des nœuds de l'arbre.
-Indiquer, en fonction du nombre de nœuds de l'arbre considéré, la complexité de la fonction calculer_arites.
-Il s'agit d'écrire en langage de programmation une fonction inserer qui prend en arguments un tableau table d'entiers non nécessairement distincts triés par valeurs décroissantes et un entier ; cette fonction modifie le tableau table pour insérer l'entier en respectant l'ordre décroissant. L'entier est inséré même s'il figure déjà dans table.
Caml : Écrire en Caml une fonction inserer telle que, si : - table est un vecteur d'entiers,
- nb est un entier positif ou nul ne dépassant pas la dimension du vecteur table diminuée de 1 ,
- d est un entier,
- on suppose que le vecteur table contient des entiers classés par valeurs décroissantes dans les cases d'indices compris entre 0 et
, les autres cases du vecteur table étant ignorées, alors inserer table nb d insère la donnée d dans le vecteur table en respectant l'ordre décroissant. La fonction renvoie , c'est-à-dire le nouveau nombre de données figurant dans table.
Pascal : Écrire en Pascal une fonction inserer telle que, si :
- table est de type Tableau,
- nb est un entier positif ou nul ne dépassant pas MAX - 1 ,
- d est un entier ;
- on suppose que le tableau table contient entre les indices 0 et
des entiers classés par valeurs décroissantes, les autres cases du tableau table étant ignorées,
alors inserer(table, nb, d) insère la donnée d dans le tableau table en respectant l'ordre décroissant. La fonction renvoie, c'est-à-dire le nouveau nombre de données figurant dans table.
23 -Indiquer, en fonction du nombre
Soit
Ainsi, le codage de Prüfer de l'arbre
24 -Indiquer le codage de Prüfer de l'arbre
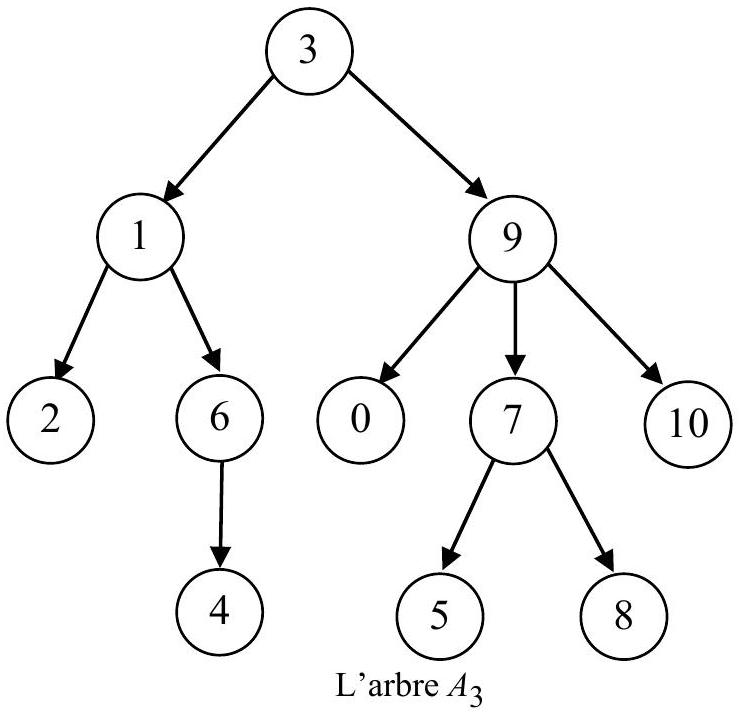
25 -On considère un arbre
Caml : Écrire en Caml une fonction calculer_Prufer telle que, si on considère un arbre
Caml : Écrire en Caml une fonction calculer_Prufer telle que, si on considère un arbre
- racine est un entier qui contient l'étiquette de la racine de
, - fils et freres sont deux vecteurs de longueur
qui représentent respectivement les tableaux fils et freres d'un codage racine-fils-frères de ,
alors calculer_Prufer racine fils freres renvoie un vecteur de longueurcontenant le codage de Prüfer de l'arbre .
Pascal : Écrire en Pascal une fonction calculer_Prufer telle que, si on considère un arbre
- racine est un entier qui contient l'étiquette de la racine de
, - fils et freres sont de type Tableau et représentent respectivement les tableaux fils et freres d'un codage racine-fils-frères de
, - n est un entier qui contient le nombre de nœuds de
,
alors calculer_Prufer(racine, fils, freres, n) renvoie un tableau, de type Tableau, contenant le codage de Prüfer de l'arbreentre les indices 0 et .
26 -Indiquer la complexité du calcul du codage de Prüfer d'un arbrepossédant nœuds, étiqueté consécutivement et codé avec le codage racine-fils-frères.
Seconde partie : d'un codage de Prüfer d'un arbre à un codage racine-fils-frères
27 - On suppose qu'on connaît le codage de Prüfer d'un arbre
Caml : Écrire en Caml une fonction calculer_arites_par_Prufer telle que, pour un arbre
Avant d'écrire la fonction calculer_arites_par_Prufer, on en donnera rapidement le principe.
Caml : Écrire en Caml une fonction calculer_arites_par_Prufer telle que, pour un arbre
Avant d'écrire la fonction calculer_arites_par_Prufer, on en donnera rapidement le principe.
Pascal : Écrire en Pascal une fonction calculer_arites_par_Prufer telle que, pour un arbre
- Prufer est de type Tableau et contient le codage de Prüfer de
, - n est un entier qui contient le nombre de nœuds de
,
alors calculer_arites_par_Prufer(Prufer, n) renvoie un tableau, de type Tableau, contenant les arités des nœuds de.
Avant d'écrire la fonction calculer_arites_par_Prufer, on en donnera rapidement le principe.
-Déterminer un arbre étiqueté consécutivement dont le codage de est: . On détaillera la démarche utilisée.
- On considère un arbre ; on suppose que l'ensemble des étiquettes de est l'arbre n'est donc pas étiqueté consécutivement ; on suppose enfin que le codage de Prüfer de est: 3, 10, 3, 7, 7, 5, 7, 5. Déterminer l'arbre . On décrira succinctement la démarche utilisée.
-Il s'agit d'écrire en langage de programmation une fonction calculer_arbre qui, à partir du codage de Prüfer d'un arbre étiqueté consécutivement, calcule un codage racine-fils-frères de .
Caml : Écrire en Caml une fonction calculer_arbre telle que, pour un arbrepossédant nœuds et étiqueté consécutivement, si : - Prufer est un vecteur de longueur
contenant le codage de Prüfer de , - fils et freres sont deux vecteurs de longueur
, alors calculer_arbre Prufer fils freres modifie les vecteurs fils et freres pour qu'ils correspondent respectivement aux tableaux fils et freres d'un codage racine-fils-frères de et renvoie l'étiquette de la racine de .
Pascal : Écrire en Pascal une fonction calculer_arbre telle que, pour un arbre
- Prufer est de type Tableau et contient le codage de Prüfer de
, - fils et freres sont de type Tableau,
- n est un entier qui contient le nombre de nœuds de
, alors calculer_arbre(Prufer, fils, freres, n) modifie les tableaux fils et freres pour qu'ils correspondent respectivement aux tableaux fils et freres d'un codage racine-fils-frères de et renvoie l'étiquette de la racine de .
Soit
