Version interactive avec LaTeX compilé
Mines Mathématiques 2 PC 2012
Équation de la chaleur
Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Calcul différentiel et fonctions à plusieurs variablesSuites et séries de fonctionsFonctions (limites, continuité, dérivabilité, intégration)Intégrales à paramètresSéries entières (et Fourier)
ÉCOLE DES PONTS PARISTECH. SUPAERO (ISAE), ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH MINES DE SAINT ÉTIENNE, MINES DE NANCY, TÉLÉCOM BRETAGNE, ENSAE PARISTECH (Filière PC). ÉCOLE POLYTECHNIQUE (Filière TSI).
CONCOURS 2012
SECONDE ÉPREUVE DE MATHÉMATIQUES
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
MATHÉMATIQUES II - PC
L'énoncé de cette épreuve comporte 4 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Equation de la chaleur
Dans ce texte on note
Le problème est consacré à l'équation de la chaleur monodimensionnelle; la fonction inconnue
où
La variable
1 Un problème aux valeurs propres
On cherche ici à déterminer les valeurs de
Question 1 Montrer que si
en déduire que si
Question 2 Pour
Question 3 Montrer que (5)-(6) possède une solution non nulle si et seulement si
Question 2 Pour
Question 3 Montrer que (5)-(6) possède une solution non nulle si et seulement si
2 La série de Fourier de la condition initiale
On note
Question 4 Tracer la courbe représentative de
On note
Question 5 Dessiner le graphe de la fonction
Soit
Soit
Question 6 Démontrer que
Question 7 Calculer
et donner l'expression de la série de Fourier de
Question 8 En déduire que la série de Fourier de
Question 8 En déduire que la série de Fourier de
3 Construction d'une solution de (1)-(2)-(3)
Pour tout
et on note
Question 9 Montrer que pour tout
Question 10 Montrer que la série de fonctions
Question 11 La série
Question 10 Montrer que la série de fonctions
Question 11 La série
converge-t-elle?.
Question 12 Soit
Question 12 Soit
Question 13 La série de fonctions
On admettra dans la suite (raisonnement analogue) que
Question 14 Montrer que u est solution de (1)-(2)-(3).
4 Unicité de la solution
Soit
Question 15 Quel est le signe de
Question 15 Quel est le signe de
On définit la dérivée à gauche
si la limite existe.
Question 16 Quel est le signe de
Question 16 Quel est le signe de
On choisit
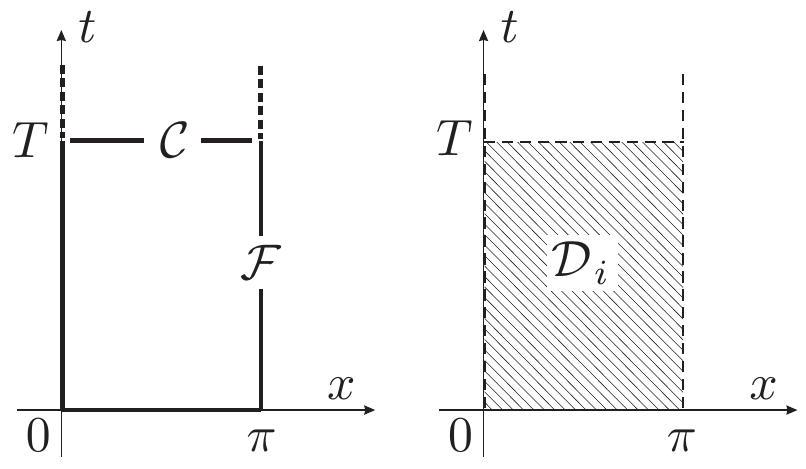
Figure 1 - Partition du domaine
Soit
Question 17 Montrer que
Notons
Question 18 Déduire de ce qui précède que u atteint son maximum sur
Question 19 Conclure que la solution de (1)-(2)-(3) est unique.
Si
Question 18 Déduire de ce qui précède que u atteint son maximum sur
Question 19 Conclure que la solution de (1)-(2)-(3) est unique.
Si
Question 20 Démontrer que
