Version interactive avec LaTeX compilé
Mines Mathématiques 2 MP MPI 2024
Notez ce sujet en cliquant sur l'étoile
5.0(1 vote)
Probabilités finies, discrètes et dénombrementRéductionAlgèbre linéaire
ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL.
Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).
CONCOURS 2024
DEUXIÈME ÉPREUVE DE MATHÉMATIQUES
L'usage de la calculatrice et de tout dispositif électronique est interdit.
L'énoncé de cette épreuve comporte 8 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Phénomènes de seuil dans les graphes
Dans ce problème,
On désigne par
Le groupe symétrique des permutations de
L'ensemble des matrices carrées d'ordre
Le cardinal d'un ensemble fini
Un graphe
On désigne par
Le groupe symétrique des permutations de
L'ensemble des matrices carrées d'ordre
Le cardinal d'un ensemble fini
Un graphe
-
désigne un ensemble fini non vide d'éléments appelés sommets du graphe -
désigne un ensemble éventuellement vide d'éléments appelés arêtes du graphe , une arête étant un ensemble où et sont des sommets distincts de .
Un sommet n'appartenant à aucune arête est dit isolé.
Par convention, le graphe vide est le couple d'ensembles vides ().
On peut représenter un graphe non vide dans un plan à l'aide : - de disques schématisant les sommets du graphe
- de segments reliant ces disques pour les arêtes du graphe.
Par exemple, on a représenté sur la Figure 1, le graphe
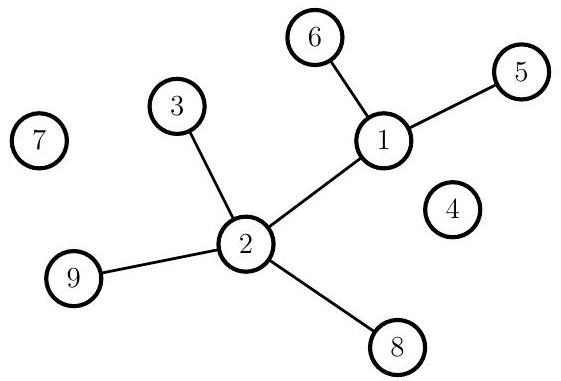
Figure 1 - un graphe à 9 sommets et 6 arêtes
On remarquera que les arêtes sont constituées de deux sommets distincts, ce qui interdit la présence de «boucles» reliant un sommet à lui-même.
De plus, une même arête ne peut être présente plusieurs fois dans un graphe.
Un type de graphe utilisé dans ce problème est l'étoile.
Une étoile de centre
Une étoile de centre
On a représenté Figure 2 une étoile de centre 4 à 5 branches avec
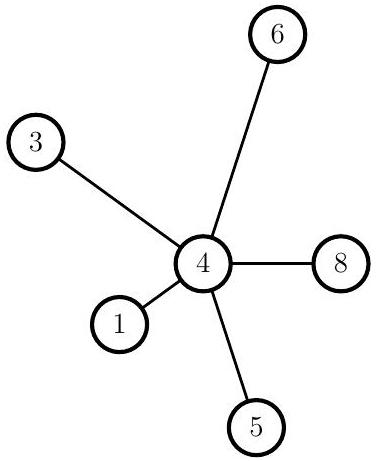
Figure 2 - une étoile à 5 branches
Soient
-
est inclus dans si et -
est une copie de s'il existe une bijection de dans telle que :
Par exemple, le graphe de la Figure 1 contient plusieurs copies d'étoiles à une branche (correspondant aux segments), plusieurs copies d'étoiles à deux branches, mais aussi une copie d'une étoile à 3 branches (de centre 1) et une copie d'une étoile à 4 branches (de centre 2).
Dans une première partie, on étudie quelques propriétés algébriques des matrices d'adjacence.
On introduit ensuite la notion de fonction de seuil en probabilité des graphes aléatoires.
Les deux parties qui suivent la première partie sont indépendantes de celle-ci, et sont consacrées à l'étude de deux exemples.
Les deux parties qui suivent la première partie sont indépendantes de celle-ci, et sont consacrées à l'étude de deux exemples.
Partie I - Quelques propriétés algébriques des matrices d'adjacence
Soit
où
Une indexation
Une indexation
On remarquera d'une part que la matrice
Voici par exemple la matrice d'adjacence
Soit
En déduire que si
En déduire que si
Si
On notera
Par convention, le polynôme caractéristique du graphe vide est le polynôme constant égal à 1 .
Donner la valeur de
Donner la valeur de
Déterminer alors les valeurs et vecteurs propres d'une matrice d'adjacence de ce graphe.
Si
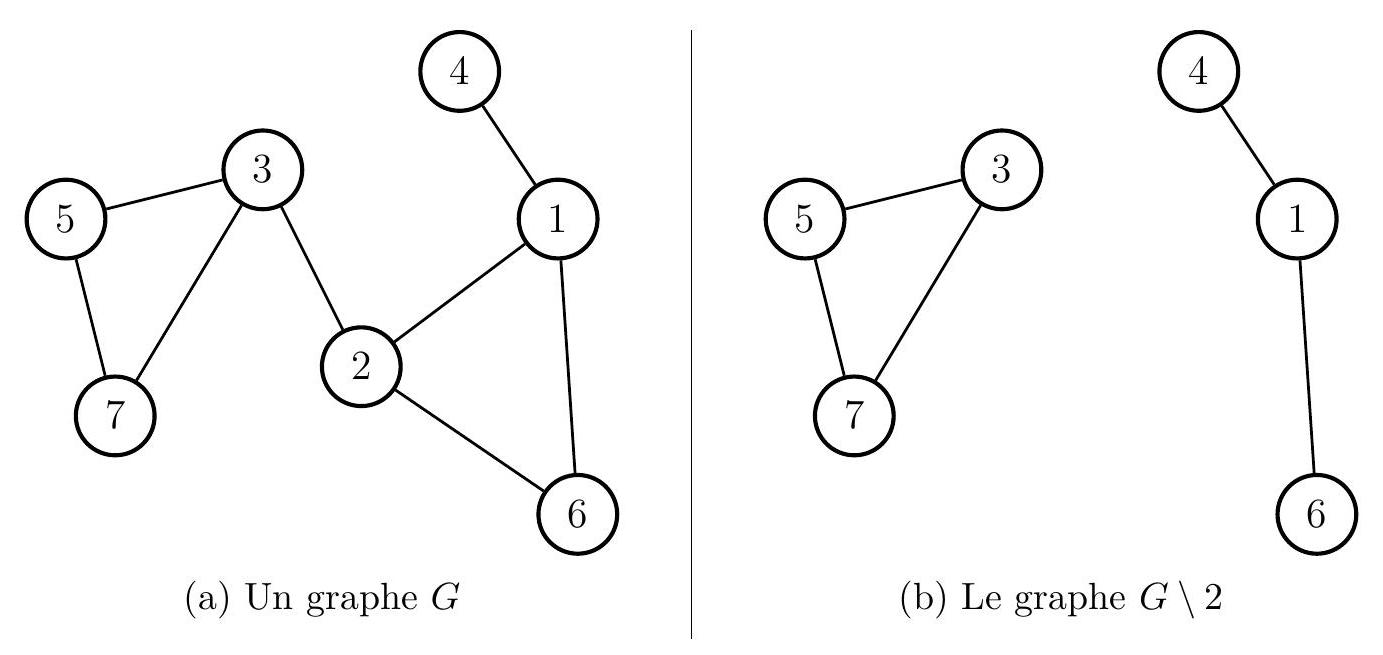
Figure 3 - un graphe
Soient
On définit le graphe
Quel est le rang de la matrice d'adjacence de cette double étoile?
Dans toute la suite de ce problème, on suppose que
-
l'ensemble des graphes de sommets -
un réel dépendant de appartenant à l'intervalle et .
Pour tous
Ainsi,
On admet l'existence d'une probabilité
Autrement dit, pour un graphe
Retrouver alors le fait que
Dans la suite du problème on étudie la notion de fonction de seuil pour une propriété
Une fonction de seuil pour la propriété
- si
alors la limite, lorsque tend vers , de la probabilité pour que la propriété soit réalisée vaut 0 - si
alors la limite, lorsque tend vers , de la probabilité pour que la propriété soit réalisée vaut 1 .
Partie II - Une première fonction de seuil
Section A - Deux inégalités
Soit
Indication : on remarquera que
Indication : on remarquera que
Section B - Une fonction de seuil
Partie III - Fonction de seuil de la copie d'un graphe
Si
Soit
Soit
On va étudier la fonction de seuil de la propriété
On note
On note
On introduit :
- l'ensemble
des copies de dont les sommets sont inclus dans :
- pour un graphe
avec , la variable aléatoire suivant une loi de Bernoulli définie par :
- le réel
défini par :
Exprimer le cardinal de
Indication : on pourra introduire
On suppose dorénavant que
Pour
et en déduire que pour
Fin du problème
- Les sujets sont la propriété du GIP CCMP. Ils sont publiés sous les termes de la licence
Creative Commons Attribution - Pas d'Utilisation Commerciale - Pas de Modification 3.0 France.
Tout autre usage est soumis à une autorisation préalable du Concours commun Mines Ponts.
