Version interactive avec LaTeX compilé
Mines Mathématiques 1 PC 2012
Le sinus lemniscatique
Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
GéométrieFonctions (limites, continuité, dérivabilité, intégration)Calcul différentiel et fonctions à plusieurs variablesIntégrales généraliséesSéries et familles sommables
A 2012 MATH I PC
ÉCOLE DES PONTS PARISTECH. SUPAERO (ISAE), ENSTA PARISTECH, TELECOM PARISTECH, MINES PARISTECH MINES DE SAINT ÉTIENNE, MINES DE NANCY, TÉLÉCOM BRETAGNE, ENSAE PARISTECH (Filière PC). ÉCOLE POLYTECHNIQUE (Filière TSI).
CONCOURS 2012
PREMIÈRE ÉPREUVE DE MATHÉMATIQUES
(Durée de l'épreuve : trois heures)
L'usage d'ordinateur ou de calculatrice est interdit.
Sujet mis à la disposition des concours : Cycle international, ENSTIM, TELECOM INT, TPE-EIVP.
L'usage d'ordinateur ou de calculatrice est interdit.
Sujet mis à la disposition des concours : Cycle international, ENSTIM, TELECOM INT, TPE-EIVP.
Les candidats sont priés de mentionner de façon apparente sur la première page de la copie :
MATHÉMATIQUES I - PC
L'énoncé de cette épreuve comporte 5 pages de texte.
Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.
Le sinus lemniscatique
Dans ce texte on note
1 La lemniscate de Bernoulli
La lemniscate de Bernoulli (voir la Figure 1) est une courbe elliptique particulièrement simple d'équation implicite
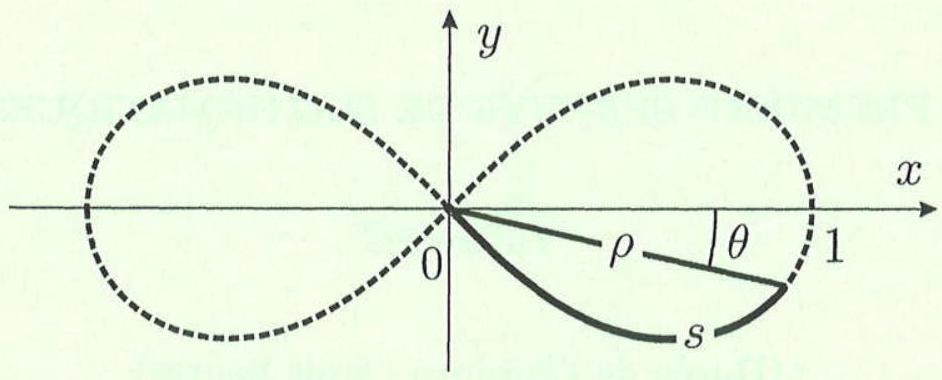
Figure 1 - La lemniscate de Bernoulli
Question 1 Déterminer dans le quart de plan
Question 2 Montrer que
Question 3 Déterminer les tangentes à la lemniscate en ( 0,0 )
Question 4 Déterminer dans le demi-plan
Question 2 Montrer que
Question 3 Déterminer les tangentes à la lemniscate en ( 0,0 )
Question 4 Déterminer dans le demi-plan
2 Le sinus lemniscatique
Question 5 Montrer que l'intégrale
On note
On note
Question 6 Que représente
On définit la fonction
Question 7 Montrer que la fonction
Question 8 Dessiner le graphe de
Question 9 Montrer que
Question 10 Donner l'expression des coefficients
Question 11 Montrer que la série de terme général
Question 12 Montrer que
Question 13 Montrer que
Question 8 Dessiner le graphe de
Question 9 Montrer que
Question 10 Donner l'expression des coefficients
Question 11 Montrer que la série de terme général
Question 12 Montrer que
Question 13 Montrer que
On prolonge la fonction
Question 14 Montrer que sl est de classe
Question 15 Tracer le graphe de sl sur
Question 15 Tracer le graphe de sl sur
3 Equation différentielle
Question 16 Montrer que sl est de classe
Soit
Question 17 Montrer que la fonction
Question 17 Montrer que la fonction
est constante sur
On choisit désormais de considérer le cas où
On choisit désormais de considérer le cas où
où
Question 18 Montrer que
Question 18 Montrer que
pour tout
Question 19 En déduire que
Question 20 Soit
Question 21 Démontrer l'existence de
Question 22 De même on pose
Question 19 En déduire que
Question 20 Soit
Question 21 Démontrer l'existence de
Question 22 De même on pose
4 Le calcul trigonométrique généralisé
La fonction cl est définie sur
Question 23 Montrer que pour tout
Question 24 Calculer la fonction dérivée
Question 25 Montrer que pour tout
Question 25 Montrer que pour tout
On définit la fonction
Question 26 Montrer que
en déduire que pour tout a dans
Question 27 Montrer que
et en déduire une formule d'addition pour la fonction sl, c'est-à-dire une expression de
Question 28 Démontrer la formule de Fagnano, valable dans un intervalle
