Cette épreuve est commune aux candidats des filières MP, PC et PSI.
Les candidats sont priés de mentionner de façon apparente
sur la première page de la copie :

INFORMATIQUE COMMUNE

L'énoncé de cette épreuve comporte 8 pages de texte.

Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

La typographie informatisée

Ce sujet explore quelques aspects de la typographie informatisée. Il aborde la gestion de polices vectorielles, leur manipulation, leur tracé, l'affichage de texte et la justification d'un paragraphe. Il va du texte à la page via le pixel. Les questions posées peuvent dépendre des questions précédentes. Toutefois, une question peut être abordée en supposant les fonctions précédentes disponibles, même si elles n'ont pas été implémentées. Les questions de programmation seront traitées en Python.

Partie I - Préambule

La typographie est l'art d'assembler des caractères afin de composer des pages en vue de leur impression ou de leur affichage sur un écran, en respectant des règles visuelles qui rendent un texte agréable à lire. Elle requiert des efforts importants, avantageusement simplifiés par le recours à l'outil informatique.

Donald Knuth, prix Turing 1974 notamment pour la monographie The Art of Computer Programming, en est un pionnier. Lassé de la piètre qualité de la typographie proposées pour son ouvrage, il développe les logiciels TEX pour la mise en page et METAFONT pour la gestion de polices. Leslie Lamport, prix Turing 2013 pour ses travaux sur les systèmes distribués, a écrit

qui facilite l'utilisation de

. IATEX est largement utilisé dans l'édition scientifique, y compris pour la composition du présent document.

Donald Knuth récompense toute personne qui signale une nouvelle erreur dans un de ses ouvrages par un chèque d'un montant de un hexa dollar, c'est-à-dire 100 cents où 100 est interprété en base hexadécimale (base 16).

Q1 Quel montant est effectivement versé en dollars par Donald Knuth pour une nouvelle erreur trouvée?
Voici la définition de quelques termes utiles pour la suite :

un caractère est un signe graphique d'un système d'écriture, par exemple le caractère latin a majuscule « A ». Le standard Unicode donne à chaque caractère un nom et un identifiant numérique, appelé point de code, que nous appellerons ci-après simplement code. Le code de « A » dans la représentation Unicode est 65 . La version 13.0 publiée en mars 2020 répertorie 143859 caractères couvrant 154 systèmes d'écriture, modernes ou historiques comme les hiéroglyphes;
un glyphe est un dessin particulier représentant un caractère, par exemple pour le caractère latin a majuscule : A (roman) (italique) (caligraphié) (gras), A (courrier)...
une police de caractères est un ensemble coordonné de glyphes incluant différentes variantes (style roman ou italique, graisse...) et permettant de représenter un texte complet dans un système d'écriture. La police de ce document est Computer Modern, la police par défaut de ;
une famille est un groupe de polices. La classification Vox-ATypI, proposée par Maximilien Vox en 1952 et adoptée par l'Association typographique internationale, contient 11 familles. La police Computer Modern fait partie de la famille Didone.
Le corps du glyphe est sa hauteur, la chasse est sa largeur. Le corps est décomposé en trois parties : l'œil qui contient typiquement les petites lettres, le jambage et la hampe qui recouvrent les dépassements en dessous ou au dessus de l'œil. La limite inférieure de l'œil est la ligne de base. Elle définit l'alignement des caractères. La chasse peut être fixe (polices

monospaces) ou variable.

La description vectorielle d'un glyphe est définie de la façon suivante :

un point p est repéré par ses coordonnées (abscisse, ordonnée) dans le plan orthonormé classique, et sera représenté par une liste de deux flottants ;
une multi-ligne 1 est une séquence de points reliés par des segments, représentée par une liste de points, éventuellement restreinte à un seul point ;
la description vectorielle v d'un glyphe est un ensemble non vide de multi-lignes, représenté par une liste de multi-lignes.
Les descriptions vectorielles seront supposées normalisées de sorte que la ligne de base corresponde à l'ordonnée 0 , que la hauteur de l'œil soit 1 , et enfin que le glyphe soit collé à l'abscisse 0 , sans dépassement vers les abscisses négatives.

Concrètement, la description vectorielle d'un glyphe est une liste de listes de listes de 2 flottants. À titre d'illustration, voici une description vectorielle d'un glyphe, composée de deux multi-lignes .

Q2 Dessiner ce glyphe. De quel caractère s'agit-il?

Partie II-Gestion de polices de caractères vectorielles

Une base de données stocke les informations liées aux polices de caractères dans 4 tables ou relations.
Famille décrit les familles de polices, avec fid la clé primaire entière et fnom leur nom.
Police décrit les polices de caractères disponibles, avec pid la clé primaire entière, pnom le nom de la police et fid de numéro de sa famille.
Caractere décrit les caractères, avec code la clé primaire entière, car le caractère lui-même, cnom le nom du caractère.
Glyphe décrit les glyphes disponibles, avec gid la clé primaire entière, code le code du caractère correspondant au glyphe, pid le numéro de la police à laquelle le glyphe appartient, groman un booléen vrai pour du roman et faux pour de l'italique et gdesc la description vectorielle du glyphe.

Voici un extrait du contenu de ces tables.

Famille
fid	fnom
1	Humane
2	Garalde
3	Réale
4	Didone
5	Mécane
6	Linéale

Police
pid	pnom	fid
1	Centaur	1
2	Garamond	2
3	Times New Roman	3
4	Computer Modern	4

21	Triangle	6

Caractere
code	car	cnom
65	A	lettre majuscule latine a
66	B	lettre majuscule latine b

97	a	lettre minuscule latine a
98	b	lettre minuscule latine b
99	c	lettre minuscule latine c

Glyphe
gid	code	pid	groman	gdesc
1	65	20	True	[ [ [0, 0], [1, 2], [2, 0] ], [ [0.5, 1], [1.5, 1] ] ]
2	65	20	False	[ [ [0, 0], [2, 2], [2, 0] ], [ [1, 1], [2, 1] ] ]
...
501	97	21	True	[ [ [0, 0], [0.5, 1], [1, 0], [0, 0] ] ]
502	98	21	True	[ [ [0, 2], [0, 0], [1, 0.5], [0, 1] ] ]
503	99	21	True	[ [ [1, 1], [0, 0.5], [1, 0] ] ]
504	100	21	True	[ [ [1, 2], [1, 0], [0, 0.5], [1, 1] ] ]

Q3 Proposer une requête en SQL sur cette base de données pour compter le nombre de glyphes en roman (cf. description précédente).

Q4 Proposer une requête en SQL afin d'extraire la description vectorielle du caractère

dans la police nommée Helvetica en italique.

Q5 Proposer une requête en SQL pour extraire les noms des familles qui disposent de polices et leur nombre de polices, classés par ordre alphabétique.

Pour la suite, la requête de la question 4 est supposée paramétrée et encapsulée dans une fonction glyphe (

) qui renvoie la description vectorielle du caractère c dans la police p en roman ou italique selon le booléen r , de sorte que l'appel à glyphe("a", "Helvetica", False) répond à la question 4.

Partie III - Manipulation de descriptions vectorielles de glyphes

L'avantage de la description vectorielle de glyphes est qu'il est possible de réaliser des opérations sur les glyphes sans perte d'information. On peut réaliser simplement un agrandissement des glyphes, une déformation de glyphe pour en créer un nouveau etc. Cette partie propose des fonctions pour analyser et modifier des descriptions vectorielles.

Dans un premier temps, des fonctions sont créées pour extraire des informations sur des glyphes. Deux fonctions utilitaires sont implémentées.

Q6 Implémenter la fonction utilitaire points(v:[[[float]]])->[float] qui renvoie la liste des points qui apparaissent dans les multi-lignes de la description vectorielle v d'un glyphe.

v = [ [ [ 0, 0 ], [ 1, 1 ] ], [ [ 0, 1 ], [ 1, 0 ] ] ]
print(points(v)) # affiche la liste [ [ 0, 0 ], [ 1, 1 ], [ 0, 1 ], [ 1, 0 ] ]

Q7 Implémenter la fonction utilitaire

qui renvoie la liste des éléments d'indice n (en commençant à 0 ) des sous listes de flottants, dont on supposera qu'ils existent toujours.

l = [ [ 1, 2 ], [ 3, 4 ], [ 5, 6 ], [ 7, 8 ] ]
print(dim(l, 1)) # affiche la liste [ 2, 4, 6, 8 ]

On cherche à déterminer les dimensions (largeur et hauteur) d'un glyphe donné de manière à pouvoir les modifier par la suite si nécessaire.

Q8 Implémenter la fonction largeur(v: [[[float]]])->float qui renvoie la largeur de la description vectorielle v. Il faudra utiliser les fonctions utilitaires précédentes ainsi que les fonctions max et min de Python appliquées à des listes.

Q9 Implémenter la fonction obtention_largeur(police:str)->[float] qui renvoie une liste de largeurs pour toutes les lettres minuscules romanes et italiques (uniquement les 26 lettres non accentuées de

) de la police police dans l'ordre a roman, a italique, b roman, b italique...

On souhaite dériver automatiquement de nouvelles représentations vectorielles de glyphes à partir de représentations existantes.

Python permet de passer simplement des fonctions en paramètre d'autres fonctions. Par exemple, la fonction applique ci-après renvoie une nouvelle liste constituée en appliquant la fonction

à tous les éléments de la liste 1 .

def applique(f:callable, l:[])->[]:
    return [ f(i) for i in l ]
def incremente(i:int)->int:
    return i + 1
print(applique(incremente, [ 0, 5, 8 ])) # affiche la liste [ 1, 6, 9 ]

Q10 En se basant sur l'exemple de la fonction applique, implémenter une fonction utilitaire transforme(f:callable, v :[[[float]]])->[[[float]]] qui prend en paramètres une fonction f , une description vectorielle v et qui renvoie une nouvelle description vectorielle construite à partir de v en appliquant la fonction

à chacun des points et en préservant la structure des multi-lignes. La fonction

passée en argument transforme un point en un autre point.

Soit la fonction

qui renvoie un nouveau point calculé de la façon suivante :

def zzz(p:[float])->[float]:
    return [ 0.5 * p[0], p[1] ]

Q11 Expliquer comment est modifiée une description vectorielle v par transforme (zzz, v). Préciser l'effet obtenu sur un glyphe.

Q12 Implémenter la fonction penche(v:[[[float]]])->[[[float]]] qui renvoie une nouvelle description vectorielle correspondant à un glyphe penché vers la droite, obtenue en modifiant comme suit les coordonnées des points

la nouvelle abscisse est ;
la nouvelle ordonnée reste .

Partic IV - Rasterisation

La rasterisation est la transformation d'une image vectorielle en image matricielle. Cette opération est indispensable notamment pour afficher à l'écran une image vectorielle.

Dans cette partie, il s'agit d'analyser comment représenter le segment entre deux points d'une représentation vectorielle par des pixels encrés dans une image bitmap.

Le module PIL (Python Image Library) fournit le sous module Image :

im = Image.new (mode, size, color=0) alloue une nouvelle image matricielle, de type bitmap si mode vaut " 1 "; le tuple size donne la largeur et la hauteur de l'image en pixels; le paramètre facultatif color précise la couleur par défaut des pixels, en bitmap 1 pour blanc et 0 pour noir ;
im.putpixel(( ), 1) attribue la valeur 1 au pixel de coordonnées ( ) de l'image im;
im.save(nom_fichier) sauvegarde l'image dans un fichier dont on donne le nom;
im.show() affiche l'image dans une fenêtre graphique.

Attention, dans le domaine graphique (images, impressions, écrans), et contrairement aux conventions mathématiques usuelles, le pixel ( 0,0 ) est le coin en haut à gauche de l'image, l'axe des ordonnées est dirigé vers le bas. Ainsi, le code suivant crée une image bitmap rectangulaire

blanche avec deux barres horizontales formant un signe

from PIL import Image
im = Image.new("1", (50, 100), color=1)
for y in range(60, 65):
    for x in range(5, 45):
        im.putpixel((x, y), 0)
        im.putpixel((x, y-20), 0)
im.save("egal.png")

La fonction trace_quadrant_est implémente une partie de l'algorithme de tracé continu de segment proposé par Jack E. Bresenham en 1962.

from PIL import Image
from math import floor # renvoie l'entier immédiatement inférieur
def trace_quadrant_est(im:img, p0:(int), p1:(int)):
    x0, y0 = p0
    x1, y1 = p1
    dx, dy = x1-x0, y1-y0
    im.putpixel(p0, 0)
    for i in range(1, dx):
        p = (x0 + i, y0 + floor(0.5 + dy * i / dx))
        im.putpixel(p, 0)
    im.putpixel(p1, 0)
im = Image.new("1", (10, 10), color=1)
trace_quadrant_est(im, (0, 0), (6, 2))
trace_quadrant_est(im, (9, 8), (1, 9))
trace_quadrant_est(im, (3, 0), (5, 8))
im.show()

Q13 Préciser les coordonnées des pixels de l'image encrés (pixels que l'on met en noir) par l'exécution de la ligne 15 ?

Q14 Préciser les coordonnées des pixels de l'image encrés par l'exécution de la ligne 16 ? Indiquer d'où vient le problème rencontré. Proposer une assertion à mettre en début de fonction pour éviter ce problème.

Q15 Préciser les coordonnées des pixels de l'image encrés par l'exécution de la ligne 17? Expliquer le problème rencontré et à quoi il est dû.

Q16 En s'inspirant du code de la fonction trace_quadrant_est, implémenter une nouvelle fonction trace_quadrant_sud qui règle le problème précédent.

Q17 Implémenter la fonction trace_segment(im:Image, p0:(int), p1:(int)) qui trace un segment continu entre les pixels p0 et p1 sur l'image im supposée assez grande. Cette fonction devra opérer correctement si les deux points passés en arguments sont égaux.

Partie V - Affichage de texte

La fonction trace_segment va maintenant permettre de tracer sur une page (comprendre une image matricielle) des glyphes à partir de leur description vectorielle.

Q18 Implémenter la fonction position(p:(float), pz:(int), taille:int)->(int) qui renvoie les coordonnées du point p (point d'un glyphe de coordonnées flottantes) en un point dans une page (pixel de coordonnées entières) de manière à ce que le point ( 0,0 ) de la description vectorielle soit en position pz sur la page, et que l'œil de taille normalisée 1 du glyphe fasse taille pixels de hauteur. Prendre garde à la bonne orientation du glyphe sur la page. Vérifier que, pour la taille limite 1, l'œil du glyphe fait bien 1 pixel de hauteur.

Q19 Implémenter la fonction affiche_car (page:Image, c:str, police:str, roman:bool, pz: (int), taille:int)->int qui affiche dans l'image page le caractère c dans la police police, en roman ou italique selon la valeur du booléen roman, et renvoie la largeur en pixel du glyphe affiché. Pour rappel, la fonction glyphe(c:str, police:str, roman:bool) charge la description vectorielle du caractère c dans la police police pour la variante roman.

from affiche import affiche_car
from PIL import Image
page = Image.new("1", (50, 50), color=1)
avance = affiche_car(page, "K", "Triangle", True, [ 10, 40 ], 16)
page.save("K.png")

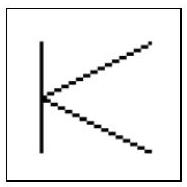
Q20 Implémenter la fonction affiche_mot(page:Image, mot:str, ic:int, police:str, roman:bool, pz: (int), taille:int)->int qui affiche la chaîne de caractères mot dans les mêmes conditions, chaque glyphe étant séparé du suivant par ic pixels, et renvoie la position du dernier pixel de la dernière lettre dans la page.

from affiche import affiche_mot
from PIL import Image
page = Image.new("1", (110, 50), color=1)
avance = affiche_mot(page, "Gödel...", 2, "Triangle", True, [ 10, 35 ], 13)
page.save("goedel.png")

De la même manière, on pourrait implémenter une fonction affiche_ligne(page:Image, ligne:[str], ic:int, im:int, police:str, roman:bool, pz:(int), taille:int) qui afficherait la liste de mots ligne en les séparant de im pixels.

Partie VI - Justification d'un paragraphe

L'objectif de cette dernière partie est d'afficher un paragraphe de manière harmonieuse en le justifiant, c'est-à-dire en alignant les mots sur les bords gauche et droit de la zone d'écriture de la page.

Lorem ipsum dolor sit amet, consectetur adipiscing elit. Sed non risus. Suspendisse lectus tortor, dignissim sit amet, adipiscing nec, ultricies sed, dolor. Cras elementum ultrices diam. Maecenas ligula massa, varius a, semper congue, euismod non, mi. Proin porttitor, orci nec nonummy molestie, enim est eleifend mi, non fermentum diam nisl sit amet erat. Duis semper. Duis arcu massa, scelerisque vitae, consequat in, pretium a, enim. Pellentesque congue. Ut in risus volutpat libero pharetra tempor. Cras vestibulum bibendum augue. Praesent egestas leo in pede. Praesent blandit odio eu enim. Pellentesque sed dui ut augue blandit sodales. Vestibulum ante ipsum primis in faucibus orci luctus et ultrices posuere cubilia Curae; Aliquam nibh. Mauris ac mauris sed pede pellentesque fermentum. Maecenas adipiscing ante non diam sodales hendrerit...

Figure 1 - Illustration de la justification de paragraphe pour différentes polices

Le paragraphe à justifier est constitué d'une liste de mots (chaînes de caractères). La difficulté est de placer des espaces entre les mots et de découper la liste en sous-listes pour que les lignes soient équilibrées (pas de ligne avec beaucoup d'espaces à la fin ou entre les mots par exemple). Pour simplifier le problème, on considère que le paragraphe est constitué d'une liste lmots d'entiers correspondant aux longueurs de chaque mot du paragraphe dans l'ordre d'apparition des mots (lmots[i] correspond au nombre de caractères du mot d'indice i). On note L le nombre de caractères et espaces que peut contenir une ligne au maximum. Il faut au minimum un espace entre deux mots d'une même ligne, on suppose que cet espace minimal correspond à un caractère.

On propose dans un premier temps l'algorithme glouton suivant :

def glouton(Lmots:[int],L:int)->[[int]]:
    lignes= []
    nligne=[]
    l=0
    for c in Lmots :
        if (c + l) > L:
            lignes.append(nligne)
            nligne=[c]
            l=c+1
        else:
            l=l+c+1
            nligne.append(c)
    lignes.append(nligne)
    return lignes

Q21 Expliquer en une ou deux phrases le principe de l'algorithme et pourquoi il est dit glouton.
Cet algorithme fournit une solution mais qui n'est pas nécessairement optimale. Si on teste cet algorithme sur le paragraphe suivant extrait du lorem ipsum : ut enim ad minima veniam pour une longueur de ligne maximale

, le résultat obtenu est le découpage noté a). Si on utilise une méthode de programmation dynamique, on obtient le découpage noté b).
a) Découpage obtenu par l'algorithme
b) Découpage obtenu par programmation glouton dynamique
ut enim ad
ut enim
minima ad minima
veniam veniam

Pour évaluer la pertinence du placement d'espaces et de retours à la ligne, on définit une fonction coût à minimiser pour que la répartition soit la plus harmonieuse possible.

Cette fonction coût correspond au nombre d'espaces disponibles sur une ligne élevé au carré, si on commence la ligne du mot

au mot

inclus sur cette même ligne :

Cette fonction prend la valeur

lorsque la somme des longueurs des mots de

est supérieure à

(ce qui signifie qu'on ne peut pas placer les mots

sur une même ligne).

La fonction python suivante correspond à l'implémentation de cette fonction coût.

def cout(i:int,j:int,lmots:[int],L:int)->int:
    res=sum(lmots[i:j+1])+(j-i)
    if res>L:
        return float("inf")
    else:
        return (L-res)**2

Q22 Évaluer pour les deux découpages a) et b) de l'exemple, ce que renvoie la fonction coût pour chacune des lignes en précisant les indices

pour chaque ligne (lmots=

). Conclure sur l'algorithme qui donne la solution la plus harmonieuse en sommant les différents coûts par ligne pour le découpage a) puis pour le découpage b).

La méthode de programmation dynamique consiste dans un premier temps à déterminer une équation de récurrence (équation de Bellman). Le problème peut être reformulé de la manière suivante :

Si on suppose connue la solution pour placer les mots jusqu'à un indice

, le nouveau problème consiste à placer correctement les changements de lignes du mot i jusqu'à la fin. La question est donc de savoir où placer le changement de ligne à partir du mot d'indice i, de manière à minimiser la fonction coût.

On note

le problème du placement optimal de changement de ligne jusqu'à l'indice i. L'équation de Bellman correspondante est alors :

Un algorithme récursif naïf correspondant à la résolution de ce problème est le suivant.

def algo_recursif(i:int,lmots:[int],L:int)->int:
    if i==len(lmots):
        return 0
    else:
        mini=float("inf")
        for j in range(i+1,len(lmots)+1):
            d=algo_recursif(j,lmots,L)+cout(i,j-1,lmots,L)
            if d<mini:
                mini=d
        return mini

Q23 Proposer une modification de la fonction algo_recursif pour rendre celle-ci plus efficace en introduisant une mémoïsation.
On définira la nouvelle fonction récursive progd_memo(i:int,lmots:[int],L:int,memo:{int:int}) avec la variable memo, dictionnaire initialisé en dehors de la fonction par memo={len(m):0}

On donne finalement une fonction utilisant la méthode de calcul de bas en haut. Cette fonction renvoie le coût optimal au problème de découpage de texte global de manière équivalente à la fonction progd_memo.

def progd_bashaut(lmots:[int],L:int)->int:
    M=[0]*(len(lmots)+1)
    for i in range(len(lmots)-1,-1,-1):
        mini,indi=float("inf"),-1
        for j in range(i+1,len(lmots)+1):
            d=M[j]+cout(i,j-1,lmots,L)
            if d<mini:
                mini,indi=d,j
        M[i]=mini
    return M[0]

Q24 Analyser, en fonction de

nombres de mots, la complexité temporelle asymptotique associée à l'algorithme récursif naïf (fonction algo_recursif) ainsi qu'à l'algorithme de programmation dynamique de bas en haut (fonction progd_bashaut) et conclure sur l'intérêt de l'algorithme de programmation dynamique. On ne comptera que les opérations de type additions/soustractions. Il n'est pas attendu de développements mathématiques poussés, les résultats peuvent être donnés sans justification.

On modifie légèrement la fonction progd_bashaut en ajoutant un argument t en plus des variables précédentes pour extraire les valeurs d'indices de découpe de lignes.

def progd_bashaut(lmots:[int],L:int,t:[int])->int:
    M=[0]*(len(lmots)+1)
    for i in range(len(lmots)-1,-1,-1):
        mini,indi=float("inf"),-1
        for j in range(i+1,len(lmots)+1):
            d=M[j]+cout(i,j-1,lmots,L)
            if d<mini:
                mini,indi=d,j
        t[i]=indi
        M[i]=mini
    return M[-1]

t[i] est la valeur de l'indice dans la liste lmots correspondant au placement optimisé sur une même ligne des mots d'indice i jusqu'à

exclus. Cette liste

est modifiée en place dans la fonction. Pour l'exemple étudié précédemment (cas b) ), on a ainsi obtenu la liste :

On dispose de la liste des mots (chaînes de caractères cette fois-ci) notée mots.
La fonction lignes (mots: [str], t : [int], L:int)->[[str]] doit renvoyer une liste de listes de mots (chaque sous-liste correspond à une ligne) en fonction de la liste t donnée par l'algorithme. La fonction lignes(["Ut","enim","ad","minima","veniam"], [2,3,4,4,5],10) renvoie:
[["Ut","enim"],["ad","minima"],["veniam"]].
De même, en prenant,

t=[2, 3, 5, 5, 5, 6, 7, 9, 11, 11, 11]
L=15
mots=["Lorem","ipsum","dolor","sit","amet,","consectetur","adipiscing",
"elit.","Sed","non","risus."]

la fonction lignes (mots,

) renvoie:

[["Lorem","ipsum"],
["dolor","sit","amet,"],
["consectetur"],
["adipiscing"],
["elit.","Sed"],
["non","risus."]]

Q25 Proposer une implémentation de cette fonction lignes(mots:[str], t : [int], L:int)
Il reste à écrire une fonction formatage(lignesdemots:[[str]],L:int) qui renvoie une chaîne de caractères correspondant à la justification du paragraphe à partir des listes de mots par ligne lignesdemots et de la longueur maximale L d'une ligne en termes de caractères et espaces. Les retours à la ligne seront représentés par le symbole "

". Les espaces devront être répartis équitablement entre les mots pour que la justification se fasse bien entre la marge gauche et la marge droite (en respectant la longueur

maximale imposée). On obtient par exemple pour

ut enim
ad minima
veniam

Q26 Proposer une implémentation de cette fonction formatage(lignesdemots: [[str]],L:int)->str qui renvoie la chaîne de caractères justifiée.

Mines Informatique Commune MP PC PSI 2023