Cette épreuve est commune aux candidats des filières MP, PC et PSI.
Les candidats sont priés de mentionner de façon apparente
sur la première page de la copie :

INFORMATIQUE COMMUNE

L'énoncé de cette épreuve comporte 12 pages de texte.

Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en expliquant les raisons des initiatives qu'il est amené à prendre.

Modélisation numérique d'un matériau magnétique

Certains matériaux particuliers peuvent acquérir des états magnétiques qualifiés de paramagnétique et ferromagnétique. Le matériau est dit paramagnétique lorsqu'il ne possède pas d'aimantation spontanée, mais acquiert une aimantation sous l'effet d'un champ magnétique extérieur. Il est dit ferromagnétique lorsqu'il possède une aimantation même en l'absence de champ magnétique extérieur. Dans ces matériaux, la température

joue un rôle crucial : si

est supérieure à une température particulière

, nommée température de Curie, le matériau adopte un état paramagnétique. Dans le cas contraire (

), il adopte un état ferromagnétique. C'est par exemple le cas du fer, pour lequel la transition entre les deux états se produit à

kelvin.

Dans un matériau magnétique, les divers éléments magnétiques (électrons, atomes) possédant un moment magnétique créent une aimantation moyenne à l'intérieur du matériau. Nous admettrons les principaux résultats de la théorie du paramagnétisme.

Ce sujet est constitué de 4 parties. Dans la première, on cherche à obtenir l'aimantation moyenne du matériau en fonction de la température à partir d'une formule théorique connue. Dans la seconde, on recherche dans une base de données les propriétés de matériaux magnétiques. Dans la troisième, on cherche à développer une modélisation microscopique d'un matériau magnétique à deux dimensions pour retrouver ce comportement (modèle d'Ising). Dans la quatrième, on s'intéresse aux domaines magnétiques du matériau (nommés domaines de Weiss).

Une courte documentation de quelques fonctions utiles est disponible à la fin du sujet.
Les candidats sont fortement incités à expliciter brièvement leurs programmes à l'aide de quelques commentaires bien placés.

L'utilisation du module numpy n'est pas autorisée.

Partie I : Transition paramagnétique/ferromagnétique sans champ magnétique extérieur

La théorie des matériaux indique que, dans un matériau ferromagnétique, l'aimantation volumique moyenne du matériau est donnée par :

où

est le nombre d'atomes par unité de volume,

est la valeur du champ magnétique à l'intérieur du matériau,

le moment magnétique des atomes ou des ions,

la constante de Boltzmann,

la température et

la fonction tangente hyperbolique.

On considère une situation sans champ magnétique extérieur. Le champ magnétique local à l'intérieur du matériau ferromagnétique est donc celui crée par la matériau lui-même. On admet que ce champ magnétique est proportionnel à l'aimantation moyenne dans le matériau (

), et on obtient alors :

En introduisant l'aimantation réduite

et la température réduite

, l'équation 1 devient :

Cette équation d'inconnue

ne possède pas de solution analytique : si on veut connaître une approximation de l'aimantation moyenne dans le matériau, il est donc nécessaire de la résoudre numériquement par une méthode de recherche de zéro.

Écrire les instructions nécessaires pour importer exclusivement les fonctions exponentielle (exp) et tangente hyperbolique (tanh) du module math, ainsi que les fonctions randrange et random du module random. Ces fonctions seront ainsi utilisables dans tous les programmes que vous écrirez ultérieurement.
A partir de l'équation 2 , indiquer une équation , d'inconnue que l'on doit résoudre et écrire en Python la définition de la fonction correspondante (paramètres et , valeur renvoyée ).
Écrire une fonction dicho(f, , , , eps) qui calcule une valeur approchée à eps près du zéro d'une fonction de variable x et de paramètre t fixé sur un intervalle . On supposera pour simplifier que la fonction dont on recherche le zéro est continue et s'annule une fois et une seule sur l'intervalle .
Établir l'expression de la complexité temporelle asymptotique de la fonction dicho en fonction de et eps.

Une étude mathématique simple permet de prouver que l'équation

n'a de solution

que pour

, ce qui revient à dire que le matériau ne possède une aimantation non nulle que pour une température inférieure à la température de Curie. On admet ainsi que si

alors

. De plus, pour

, on admet que la solution

ne doit pas être prise en compte car elle correspond à une solution instable.
5. En utilisant la fonction dicho, écrire une fonction construction_liste_m(t1, t2) qui construit et retourne une liste de 500 solutions de l'équation (1), pour

variant linéairement de

(bornes incluses). On cherchera les valeurs de

près avec un intervalle de recherche initial

.
En traçant l'aimantation

en fonction de la température

, on obtient le graphe de la figure 1 permettant de visualiser les domaines ferromagnétique (

) et paramagnétique (

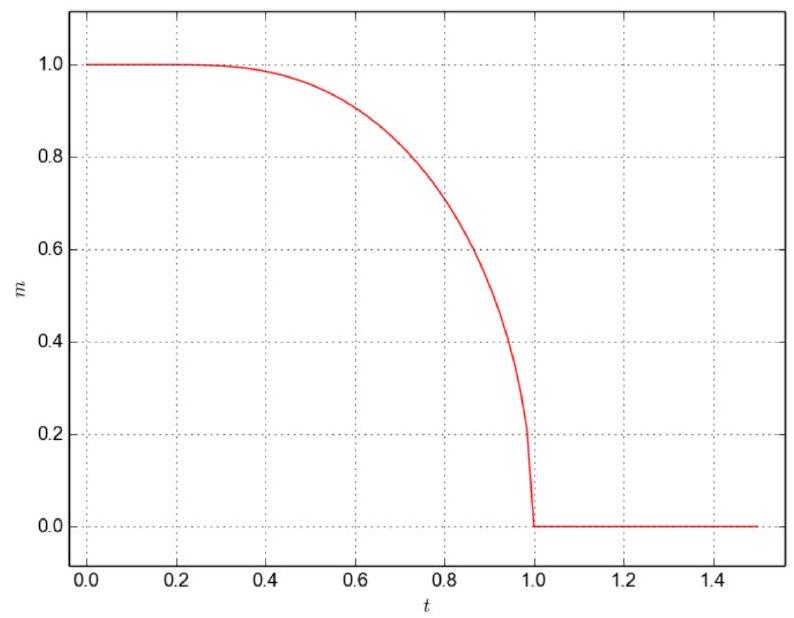
Figure 1 - aimantation réduite

en fonction de la température réduite

Partie II : Recherche dans une base de données de matériaux magnétiques

Il existe des bases de données contenant les propriétés de nombreux matériaux, dont des propriétés magnétiques. Dans cette partie, on donne un modèle simplifié d'une telle base, et on souhaite effectuer quelques requêtes sur celle-ci.

La base de données possède la structure suivante :

La table materiaux contient un champ id_materiau, clé primaire de la table de valeur entière, un champ nom de type chaîne de caractères pour le nom du matériau et un champ t_curie de valeur entière pour la température de Curie du matériau en kelvin.

id_materiau	nom	t_curie
4534	cobalt	1388
1254	dioxyde de chrome	386
8713	nickel	627
8284	YIG	560

La table fournisseurs, contenant un champ id_fournisseur, clé primaire de type entier qui précise le code de chaque fournisseur, et un champ nom_fournisseur de type chaîne de caractères pour le nom du fournisseur.

id_fournisseur	nom_fournisseur
145	Worldwide Materials
13	Materials Company

La table prix qui contient un champ id_prix, clef primaire de type entier, un champ id_mat dont les valeurs sont incluses dans l'ensemble des valeurs de la clé id_materiau de la table materiaux, un champ id_four dont les valeurs sont incluses dans l'ensemble des valeurs de la clé id_fournisseur de la table fournisseurs, et un champ prix_kg de type flottant qui précise le prix au kg que ce fournisseur propose pour ce matériau, en euros. Un fournisseur qui ne propose pas un matériau donné n'a pas d'entrée correspondante dans cette table.

id_prix	id_mat	id_four	prix_kg
1	4567	145	50.40
2	8671	13	1357.30
3	1763	145	52.75

Les requêtes demandées dans cette partie sont à écrire en langage SQL.
6. Écrire une requête permettant d'obtenir le nom de tous les matériaux qui ont une température de Curie strictement inférieure à 500 kelvins.

Un client potentiel souhaite acheter 4,5 kilogrammes de nickel (d'identifiant 8713, que l'on pourra utiliser directement dans les requêtes) et sélectionner le fournisseur le moins cher.
7. Écrire une requête permettant d'obtenir les noms de tous les fournisseurs proposant du nickel et le prix proposé par chacun pour 4,5 kilogrammes de nickel.
8. Modifier ou compléter la requête précédente afin d'obtenir le nom du fournisseur de nickel le moins cher ainsi que le prix à payer chez ce fournisseur pour ces 4,5 kilogrammes de nickel. En cas d'égalité du prix optimal entre plusieurs fournisseurs, on obtiendra les noms de tous les fournisseurs possibles.
9. Écrire une requête permettant d'obtenir le nom de tous les matériaux et le prix moyen pour un kilogramme de chacun de ces matériaux (la moyenne étant calculée pour tous les fournisseurs proposant ce matériau), en se limitant aux prix moyens strictement inférieurs à 50 euros par kilogramme.

Partie III : Modèle microscopique d'un matériau magnétique

Pour étudier l'effet du champ magnétique sur un matériau magnétique, on adopte une modélisation microscopique. On modélise les atomes par des sites portant chacun une grandeur physique, nommée spin, dont il n'est pas nécessaire de connaître les propriétés.

L'échantillon modélisé est une zone carrée à deux dimensions possédant

spins régulièrement répartis dans chaque direction, donc formant une grille carrée de

spins. Chaque spin ne possède que deux états down ou up, ce que l'on modélise par une variable

Figure 2 - Modèle des spins dans un matériau ferromagnétique

Pour implémenter cette configuration de spins décrivant l'état microscopique du matériau, on choisit de travailler sur une liste

, contenant

entiers, chacun valant -1 ou 1 . On notera le choix d'implémentation adoptée, qui impose de travailler sur une simple liste de

éléments pour modéliser une grille de taille

, dans l'ordre suivant : première ligne puis deuxième ligne, etc.

Un domaine d'aimantation uniforme (cf. figure 2) sera donc représenté par une liste contenant

fois

Le début du programme, outre les imports de module Python déjà réalisés à la question 1, est défini par :

h = 100
n = h**2

ce qui définit deux variables globales utilisables dans tout le programme.
10. Écrire une fonction initialisation() renvoyant une liste d'initialisation des domaines contenant n spins de valeur 1 comme sur la figure 2 .
L'antiferromagnétisme est une propriété de certains milieux magnétiques. Contrairement aux matériaux ferromagnétiques, dans les matériaux antiferromagnétiques, l'interaction d'échange entre les atomes voisins conduit à un alignement antiparallèle des moments magnétiques atomiques (cf. figure 3). L'aimantation totale du matériau est alors nulle (on se limite au cas où

est pair).

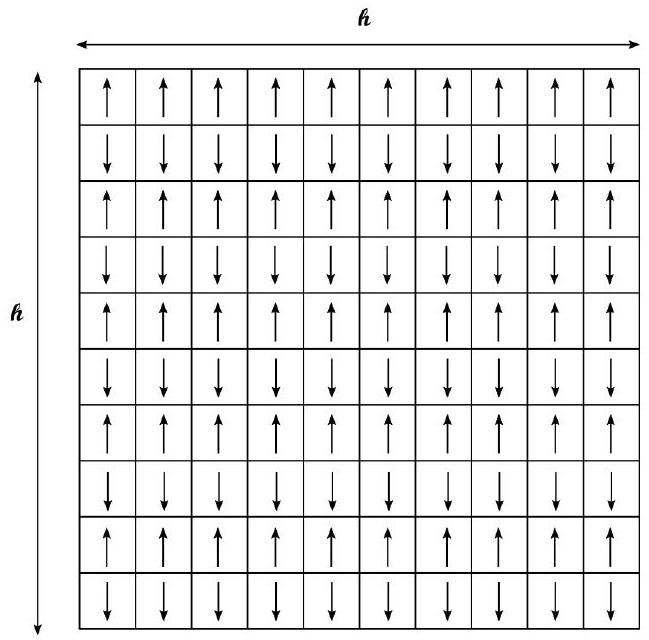
Figure 3 - Modèle des spins d'un matériau antiferromagnétique

Écrire une fonction initialisation_anti() renvoyant une liste s d'initialisation des domaines contenant spins en largeur et en hauteur en alternant les 1 et -1 comme sur la figure 3 .
Pour afficher l'état global du matériau, il est nécessaire de convertir la liste utilisée en un tableau de taille représenté par une liste de listes. Écrire une fonction repliement(s) qui prend en argument la liste de spins s et qui renvoie une liste de listes de taille représentant le domaine.
Attention : dans la suite, l'utilisation de la fonction repliement n'est pas autorisée : on travaille exclusivement sur une liste unidimensionnelle .

Dans la modélisation adoptée (sans champ magnétique extérieur), l'énergie d'une configuration, définie par l'ensemble des valeurs de tous les spins, est donnée par :

avec

l'ensemble des voisins du spin

.
On suppose que seuls les quatre spins situés juste au dessus, en dessous, à gauche et à droite de

sont capables d'interagir avec lui.

est nommée intégrale d'échange et modélise l'interaction entre deux spins voisins. Pour simplifier, on considérera dans les programmes que

Malgré le caractère fini de l'échantillon, on peut utiliser une modélisation très utile pour faire comme s'il était infini en utilisant les conditions aux limites périodiques. Lorsque l'on considère un spin dans la colonne située la plus à droite (resp. gauche), il ne possède pas de plus proche voisin à droite (resp. gauche) : on convient de lui en affecter un, qui sera situé sur la même ligne complètement à gauche (resp. droite) de l'échantillon . De même, le plus proche voisin manquant d'un spin situé sur la première (resp. dernière) ligne sera situé sur la dernière (resp. première) ligne de l'échantillon (voir la figure 4).

Figure 4 - Voisinage d'un spin (les voisins des spins sur les cases noires sont indiqués en gris)

Définir une fonction liste_voisins(i) qui renvoie la liste des indices des plus proches voisins du spin d'indice i dans la liste s (dans l'ordre gauche, droite, dessous, dessus). On pourra utilement utiliser les opérations % et // de Python, qui renvoient le reste et le quotient de la division euclidienne.
Définir la fonction energie(s) qui calcule l'énergie d'une configuration donnée (cf. équation .
Pour trouver une configuration stable pour les spins, il faut faire évoluer la liste vers une situation d'équilibre conformément aux principes de la physique statistique. On adopte une méthode probabiliste connue sous le nom de méthode de Monte-Carlo, dont le principe de fonctionnement est le suivant. À chaque étape :

on choisit un spin au hasard dans l'échantillon,
on calcule la variation d'énergie qui résulterait d'un changement d'orientation de ce spin,
si , ce spin change de signe,
si , ce spin change de signe avec la probabilité donnée par la loi de Boltzmann :

Dans la suite,

seront désignées par les variables delta_e et T correspondantes dans le programme.
15. Définir une fonction test_boltzmann(delta_e, T) qui renvoie True si le spin change de signe, et False sinon.
16. Juste après avoir sélectionné au hasard l'indice i d'un spin de la liste s à basculer éventuellement, pour évaluer l'écart d'énergie delta_e entre les deux configurations avant/après, on propose deux solutions sous forme des fonctions calcul_delta_e1 et calcul_delta_e2 :

def calcul_delta_e1(s, i):
    s2 = s[:]
    s2[i] = -s[i]
    delta_e = energie(s2)-energie(s)
    return delta_e
def calcul_delta_e2(s, i):
    delta_e = 0
    for j in liste_voisins(i):
        delta_e = delta_e + 2*s[i]*s[j]
    return delta_e

où

est le spin choisi pour être éventuellement retourné. Indiquer la solution qui vous paraît la plus efficace pour minimiser le temps de calcul en justifiant votre réponse.
17. En utilisant la fonction test_boltzmann, définir une fonction monte_carlo(s, T, n_tests) qui applique la méthode de Monte-Carlo et qui modifie la liste

où l'on a choisi successivement n_test spins au hasard, que l'on modifie éventuellement suivant les règles indiquées dans les explications.
18. Écrire la fonction aimantation_moyenne(n_tests, T) qui :

initialise une liste des spins (avec la fonction initialisation par exemple),
la fait évoluer en effectuant n_tests tests de Boltzmann et les inversions éventuelles qui en découlent,
calcule et renvoie l'aimantation moyenne de la configuration à la température T (définie ici comme la somme des valeurs des spins divisée par le nombre total de spins).

Évaluer la complexité asymptotique de la fonction aimantation_moyenne(n_tests, T) en fonction de n, nombre de spins dans le système, et de n_tests.
Cette complexité asymptotique serait-elle modifiée si on avait voulu prendre en compte toutes les interactions entre deux spins quelconques dans le système, et plus seulement entre les plus proches voisins? Justifier.

On réalise plusieurs simulations en faisant varier la température

autour de la température de Curie (ici

compte-tenu du choix des valeurs de

). On représente alors les spins orientés vers le haut par une case foncée et les spins orientés vers le bas par une case claire. On obtient les résultats de la figure 5.

Figure 5 - Évolution du domaine en fonction de la température

Indiquer l'influence de l'augmentation de la température sur le comportement du matériau ferromagnétique.

Partie IV : Exploration des domaines de Weiss

Une observation microscopique des matériaux magnétiques nous apprend que les zones magnétiques du matériau sont organisées en domaines, nommés domaines de Weiss. Dans un domaine de Weiss donné, tous les spins ont la même valeur.

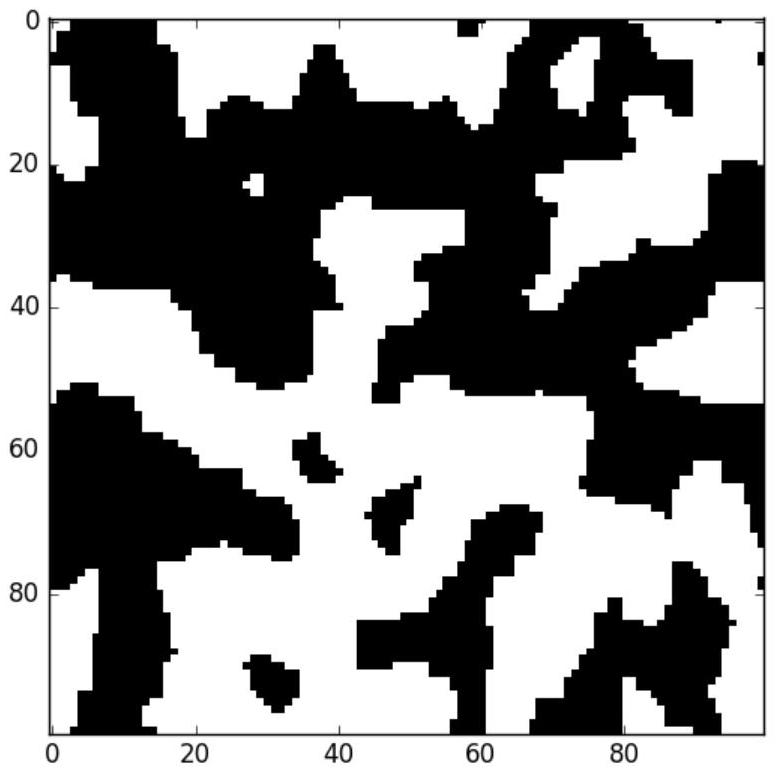
Figure 6 - Représentation des domaines de Weiss

On souhaite dans la suite décrire les différents domaines de Weiss afin, par exemple, de les colorier d'une manière différente. Pour cela, on va construire une liste, nommée weiss, possédant exactement la même taille que s (soit n ) contenant initialement des -1 (cette valeur signifiant que le spin correspondant n'a encore été affecté à aucun domaine de Weiss).

On souhaite alors écrire une fonction récursive explorer_voisinage(s, i, weiss, num) qui, à partir d'une configuration donnée

, d'un indice de départ i (repérant le spin dans

), ainsi qu'un entier num qui précise le numéro du domaine auquel appartient

, construit récursivement la liste weiss par effet de bord. Cette fonction doit réaliser les opérations suivantes :

Pour chaque spin voisin du spin , elle doit vérifier si les spins sont identiques, et s'il n'a pas déjà été affecté à un domaine de Weiss précédemment.
Dès qu'un tel spin est ajouté, on inscrit son numéro de domaine dans la liste weiss, et on explore récursivement son voisinage.

Écrire le code de la fonction récursive explorer_voisinage(s, i, weiss, num) conforme à la description ci-dessus.

Avec la fonction précédente, la pile de récursion peut devenir de taille très importante dans le cas d'un domaine de grande taille. Afin de mieux contrôler ce parcours, on choisit de l'effectuer avec une structure de pile explicite. Cette pile sera représentée par une liste nommée pile sur laquelle on peut ajouter un élément (avec append) ou récupérer l'élément du dessus (via pile.pop() qui renvoie l'élément sur le dessus de la pile et le retire de la pile). Il s'agit donc, tant qu'il reste des spins à explorer, de :

récupérer l'indice d'un spin à explorer dans la pile et le marquer dans la liste weiss,
regarder dans son voisinage si des spins possèdent la même valeur et n'ont pas encore été affectés à un domaine, puis ajouter leurs indices dans la pile si c'est le cas.

Écrire le code de la fonction itérative explorer_voisinage_pile(s, i, weiss, num, pile) conforme à la description ci-dessus.

Enfin, la fonction précédente va permettre de construire la liste weiss contenant les numéros des domaines auxquels appartiennent tous les spins (le numéro du domaine auquel appartient le spin d'indice 0 sera pris à 0 , le domaine suivant à 1 , etc.).
24. Écrire le code de la fonction weiss=construire_domaines_weiss(s) qui construit et renvoie la liste weiss contenant le numéro des domaines de Weiss de chaque spin du domaine.

L'intérêt de la construction précédente est de disposer d'un marqueur différent pour chaque domaine de Weiss, permettant par exemple de les visualiser dans deux dimensions avec des couleurs différentes, comme dans l'image de la figure 7 :

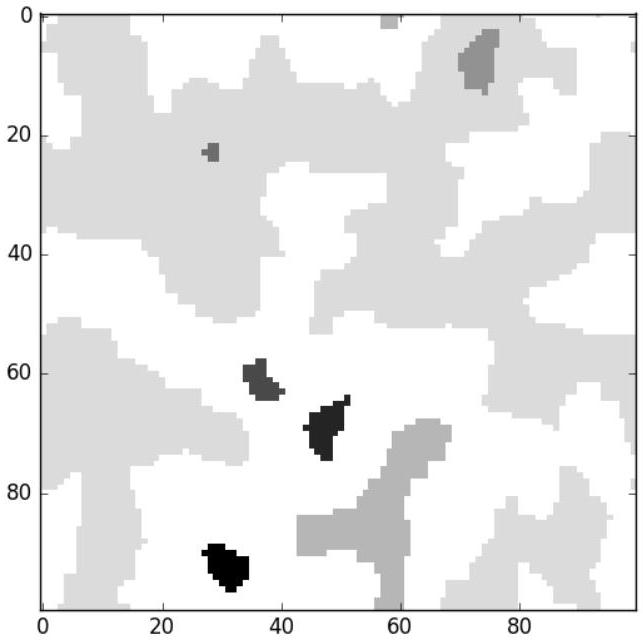
Figure 7 - Domaines de Weiss après marquage en nuances de gris

Fin de l'épreuve

Annexe : Documentation sommaire

Les fonctions présentées ci-dessous pourront être utilisées sous réserve de l'import du module Python auquel elles appartiennent.

Module math : les fonctions exp et tanh permettent de calculer l'exponentielle et la tangente hyperbolique d'un entier ou d'un flottant.
Module random :
randrange(n) permet de renvoyer un entier aléatoirement choisi parmi
random() permet de renvoyer un flottant aléatoire entre 0 et 1 suivant une densité de probabilité uniforme.
On admet que ces deux fonctions sont de complexité constante.

Mines Informatique Commune MP PC PSI 2022

Modélisation numérique d'un matériau magnétique

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL. Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).

CONCOURS 2022

ÉPREUVE D'INFORMATIQUE COMMUNE

Durée de l'épreuve : 2 heures

INFORMATIQUE COMMUNE

Modélisation numérique d'un matériau magnétique

Partie I : Transition paramagnétique/ferromagnétique sans champ magnétique extérieur

Partie II : Recherche dans une base de données de matériaux magnétiques

Partie III : Modèle microscopique d'un matériau magnétique

Partie IV : Exploration des domaines de Weiss

Fin de l'épreuve

Annexe : Documentation sommaire

ÉCOLE DES PONTS PARISTECH, ISAE-SUPAERO, ENSTA PARIS, TÉLÉCOM PARIS, MINES PARIS, MINES SAINT-ÉTIENNE, MINES NANCY, IMT ATLANTIQUE, ENSAE PARIS, CHIMIE PARISTECH - PSL.
Concours Mines-Télécom, Concours Centrale-Supélec (Cycle International).