L'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé. Cependant, une seule calculatrice à la fois est autorisée sur la table ou le poste de travail, et aucun échange n'est autorisé entre les candidats.

Les cinq parties du problème sont totalement indépendantes. Un résultat utile à une autre partie est toujours donné dans l'énoncé.

Le candidat est prié d'accorder un soin particulier à la clarté et à la concision de ses réponses et aux applications numériques demandées.

L'attention du candidat est attirée sur le fait que pour des raisons de lisibilité, les figures de l'énoncé ne sont pas nécessairement à l'échelle : en particulier, les déplacements et les déviations angulaires des différents oscillateurs considérés sont toujours grandement exagérés.

La représentation graphique demandée à la question 4.4.2 doit être effectuée sur une des deux feuilles fournies avec le sujet.

Étude de la force de Casimir

Le problème porte sur l'étude d'un effet découvert théoriquement en 1948 par Hendrik Casimir et qui porte son nom : la force de Casimir. Cette force s'exerce entre deux plans parallèles conducteurs non chargés. Cet effet étant extrêmement faible, il a fallu attendre ces dernières années pour le mesurer avec une précision relative de l'ordre d'un pour cent.
L'existence de cette force est liée aux propriétés quantiques du rayonnement : son étude est donc hors programme. De nombreux aspects des expériences la mesurant peuvent néanmoins être traités.

La première partie propose une introduction au problème de la précision d'une mesure : description théorique, influence du nombre de mesures et un modèle microscopique simple pour décrire l'exemple important que constitue le mouvement d'agitation thermique.
La seconde partie propose une première approche de la force de Casimir : explication qualitative du signe de la force et dépendance avec la distance entre les plans.
Les troisième, quatrième et cinquième parties s'intéressent chacune à une expérience récente sur le sujet : mesure de la force dans une configuration plan-plan (la plus simple à décrire théoriquement), mesure dans une géométrie plan-sphère (la plus simple à mettre en oeuvre expérimentalement) et étude de l'influence de la force de Casimir sur le comportement dynamique d'un micro-oscillateur mécanique.

Dans tout le problème, on néglige la force de pesanteur.

Constantes physiques

Nom	Symbole	Valeur	Unité
Constante de Planck
Constante de Boltzmann
Vitesse de la lumière dans le vide
Permittivité diélectrique du vide

Notation

Les grandeurs vectorielles comme le champ électrique

sont notées en gras.

Définition

On définit la fonction erf par :

Formulaire

1 Préambule : précision d'une mesure

Toute mesure d'une grandeur physique est entachée d'une incertitude expérimentale, qu'il convient d'estimer et de contrôler. Dans cette partie, on s'intéresse à l'influence du nombre de mesures sur la précision avec laquelle on peut déterminer une grandeur physique, ainsi qu'à un modèle microscopique simple du mouvement d'agitation thermique.

1.1 Précision combinée de plusieurs mesures

La mesure expérimentale d'une grandeur physique

est généralement décrite par la donnée de deux grandeurs caractéristiques : sa valeur moyenne

et son écart-type

, définis par :

où les

représentent la valeur moyenne sur l'ensemble des mesures effectuées.

Montrer que si l'on mesure une grandeur , où et sont deux grandeurs indépendantes l'une de l'autre, alors l'incertitude expérimentale vérifie :

En déduire qu'en effectuant mesures indépendantes de la même grandeur, on peut diminuer l'influence de l'incertitude expérimentale par un facteur .
Pourquoi une erreur systématique telle qu'une erreur de calibration d'un appareil ne vérifie-t-elle pas cette loi?

1.2 Exemple du mouvement d'agitation thermique

Cette section propose une approche simple d'un exemple important de facteur pouvant limiter la précision d'une mesure: le mouvement d'agitation thermique.
Dans toute cette section, on se limite à des mouvements à une dimension.
On s'intéresse à un gaz mixte de particules, contenant à la fois des particules (1) (de masse

) et des particules ( 2 ) (de masse

). On ne prend en compte que les collisions élastiques mettant en jeu une particule de type (1) et une de type (2). La durée des collisions est supposée infinimente courte.

1.2.1 Étude d'une collision

On note

(respectivement

) les composantes des vitesses des particules (1) et (2) juste avant (resp. juste après) la collision.

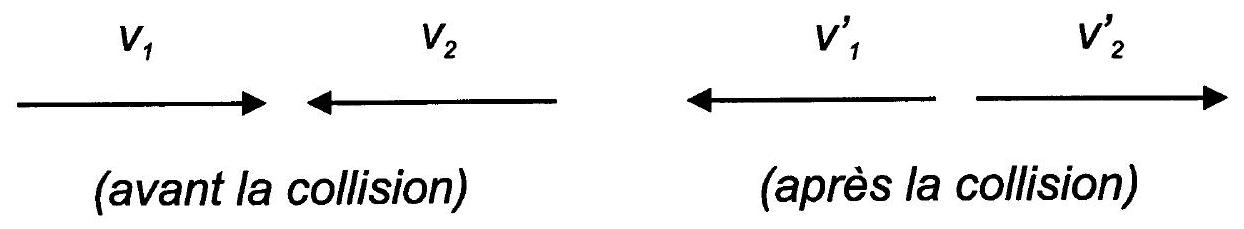
Fig. 1 - Schéma de la collision.

Écrire en les justifiant deux relations reliant ces grandeurs entre elles.
En déduire et en fonction des vitesses initiales et des masses des particules.
Montrer que la variation d'énergie cinétique de la particule (1) au cours de la collision s'écrit :

1.2.2 Établissement d'un équilibre

Å

, on met en contact un grand nombre de particules de type (1) initialement sans vitesse initiale avec le même nombre de particules (2), qui présentent une distribution isotrope de vitesses

et une énergie cinétique moyenne

. Pendant un intervalle de temps

, on suppose que chaque particule subit une collision et une seule avec une particule de l'autre espèce.
On note

l'énergie cinétique moyenne des particules (i) après

intervalles de temps

Montrer que sur l'ensemble des collisions, a une valeur moyenne nulle.
Établir une relation de récurrence entre et pour .
En déduire que les deux suites tendent vers une limite commune .
Exprimer en fonction des données du problème. À quoi est-il alors naturel de la poser égale?
Comment qualifieriez-vous la convergence? Estimer le nombre de collisions nécessaire pour atteindre l'équilibre.
La prise en compte des collisions entre particules de même type a-t-elle une incidence sur le raisonnement précédent?

1.2.3 Mouvement d'agitation thermique d'un oscillateur harmonique

On s'intéresse maintenant à la conséquence de ce mouvement d'agitation thermique sur un oscillateur harmonique au contact de ce gaz de particules. On modélise cet oscillateur comme un ressort de masse nulle et de raideur

, fixé à une paroi à une de ses extrémités, et auquel une masse

est fixée à l'autre.

Quelle est la fréquence de résonance de cet oscillateur?
L'oscillateur harmonique est supposé initialement au repos.
(a) Pourquoi peut-on analyser les collisions entre les particules du gaz et la masse sans tenir compte du ressort, c'est-à-dire comme au paragraphe précédent?

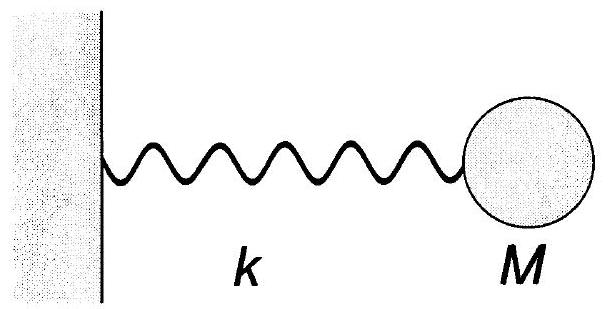
Fig. 2 - Modélisation de l'oscillateur harmonique de fréquence de résonance

: une masse

reliée à un ressort de masse nulle et de raideur

(b) Dans la limite

, montrer que l'énergie potentielle élastique moyenne de l'oscillateur tend également vers

.
3. Quel théorème retrouve-t-on?

2 Force de Casimir

Dans cette partie, on s'intéresse à un système constitué de deux plans parallèles identiques, supposés parfaitement conducteurs et portés au même potentiel électrostatique. Les deux plans sont espacés d'une distance

. On note

leur surface. On néglige les effets de bord liés à leur extension transverse finie dans le plan

. On cherche à établir quelques propriétés simples de la force de Casimir qui s'exerce entre eux.

2.1 Modes d'une cavité linéaire

On s'intéresse ici au système que forment les deux plans du point de vue de l'électromagnétisme, c'est-à-dire à la cavité électromagnétique associée.

Quelles sont les conditions aux limites qu'impose le métal parfaitement réfléchissant au champ?
Quelle conséquence cela a-t-il pour une onde électromagnétique incidente de façon normale sur un plan métallique?
On se limite à des ondes électromagnétiques planes se propageant selon l'axe ( ) de la cavité formée par les deux plans métalliques.
(a) Quelle équation de propagation le champ électrique vérifie-t-il?
(b) En tenant compte des conditions aux limites, déterminer les fréquences propres de la cavité, c'est-à-dire les fréquences pour lesquelles il existe une solution en onde stationnaire vérifiant à la fois l'équation de propagation et les conditions aux limites et donner la forme générale du champ dans la cavité.

2.2 Interprétation qualitative de la force

À chaque mode du champ électromagnétique est associée une force de pression de radiation dont on montre en électromagnétisme classique qu'elle est proportionnelle à l'intensité lumineuse. En électrodynamique quantique, cette force ne s'annule jamais, même pour une intensité nulle, c'est-à-dire en l'absence de tout photon. C'est cette pression de radiation du vide qui est à l'origine de la force de Casimir : le nombre supérieur de modes à l'extérieur de la cavité formée par les deux

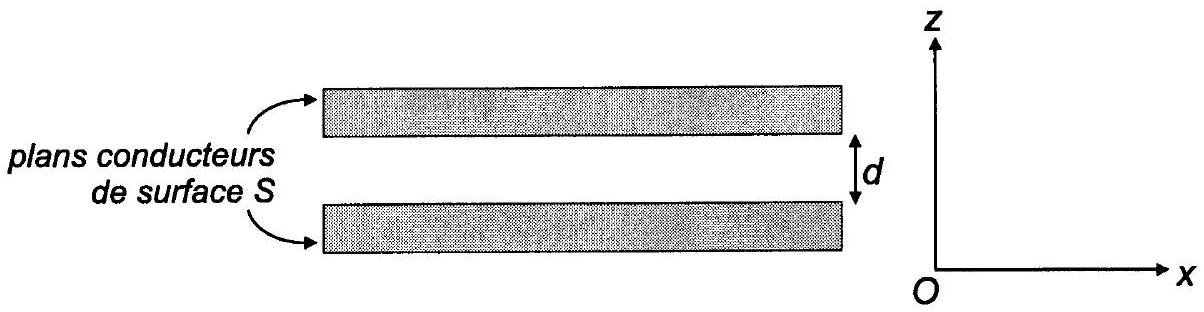
Fig. 3 - Géométrie considérée dans l'article original de Casimir : deux plans métalliques parallèles portés au même potentiel.

plans conducteurs entraîne un déséquilibre de la pression de radiation et une force attractive entre eux.

D'après cette interprétation, le module de la force augmente-t-il ou diminue-t-il quand on diminue la distance

2.3 Dépendance avec les grandeurs du problème

Montrer que la force est proportionnelle à la surface des plans.
En déduire que la pression de Casimir entre deux plans conducteurs séparés d'une distance peut se mettre sous la forme :

où

est une constante sans dimension, dont on admettra la valeur

.
3. Application numérique : pour quelle distance de séparation cette pression est-elle du même ordre de grandeur que la pression atmosphérique?

2.4 Effets correctifs

En pratique, aucun métal n'est parfaitement réfléchissant à toutes les longueurs d'onde. Dans quel sens cela corrige-t-il la valeur de la force de Casimir?
À l'échelle microscopique, toutes les surfaces présentent des irrégularités.
(a) On représente ces irrégularités par un profil à deux dimensions, avec :

étant appelée la rugosité de la surface, qu'on suppose égale pour les deux surfaces. En sommant les forces de Casimir sur des surfaces élémentaires, montrer qu'on obtient une correction à la force au second ordre en

.
(b) Quelle rugosité maximale peut-on tolérer pour un miroir optique utilisé en laboratoire?
(c) Quelle rugosité minimale peut-on espérer atteindre en polissant une surface?
(d) Ces rugosités sont-elles compatibles avec l'objectif de mesurer la force de Casimir avec une précision de

pour des distances

de l'ordre du micron?

3 Expérience d'Onofrio

On s'intéresse dans cette partie à une expérience réalisée en 2001 par Roberto Onofrio et ses collaborateurs, qui a permis de mesurer directement la force de Casimir entre deux plans métalliques pour des séparations de l'ordre du micron.

Un plan est ici constitué d'une micro-poutre en silicium (

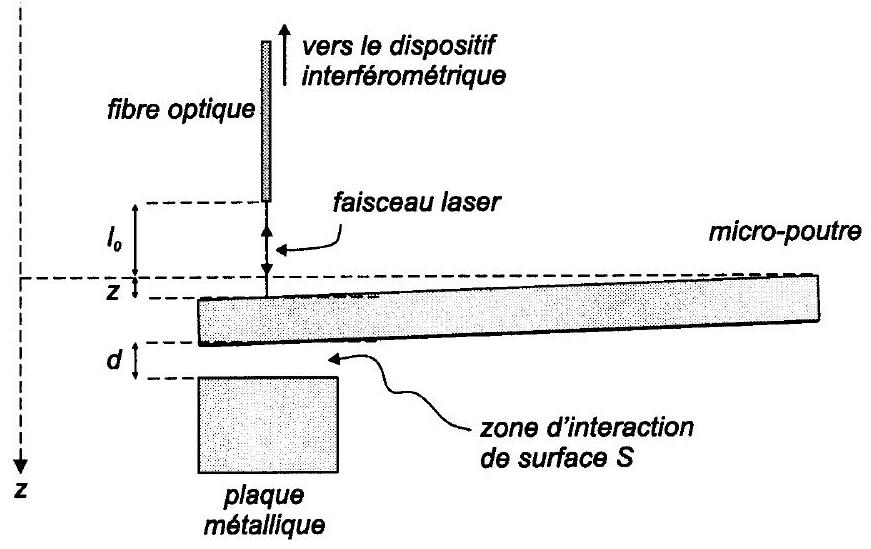
), sur laquelle on a réalisé un dépôt métallique. Une cale piézo-électrique permet de contrôler la distance d'approche

Fig. 4 - Schéma du dispositif expérimental utilisé par Onofrio. La force de Casimir entre deux plans séparés d'une distance

entraîne une flexion de la micro-poutre et un déplacement de son extrémité, qui est mesuré par un dispositif interférométrique.

du second plan métallique. Les deux plans sont parallèles et présentent une surface d'interaction

. Le parallélisme de l'ensemble est contrôlé en faisant pivoter le second plan avec un moteur pas-à-pas. L'autre face de la micro-poutre est polie de façon à pouvoir réfléchir un faisceau laser utilisé pour mesurer son déplacement.

On s'intéresse successivement au principe de la mesure de force employée dans cette expérience et au capteur interférométrique qui permet de suivre les mouvements de l'extrémité de la micropoutre.

3.1 Principe de la mesure de force

En pratique, le mouvement de l'extrémité de la micro-poutre peut être décrit par celui d'un oscillateur harmonique de fréquence propre

et de masse

. Sauf indiqué expressément, on néglige l'amortissement de cet oscillateur.

Écrire l'équation du mouvement de l'extrémité de la poutre autour de sa position d'équilibre sous l'effet combiné de la force de rappel élastique et de la force de Casimir.
La linéariser en faisant l'hypothèse que .
En déduire que sous l'effet de la force de Casimir, la fréquence de résonance de l'oscillateur est décalée. Donner l'expression de la fréquence de résonance modifiée en fonction des données du problème.
Calculer un ordre de grandeur du décalage de fréquence pour une distance de l'ordre du micron.
En supposant qu'on est capable de détecter le mouvement de la micro-poutre, proposer brièvement un protocole de mesure des variations de la force de Casimir avec la distance.
La prise en compte de l'amortissement, et donc de la largeur de la résonance de l'oscillateur, entraîne-t-elle des contraintes expérimentales supplémentaires?
Comment serait-il judicieux de représenter les résultats expérimentaux pour vérifier la loi établie à la question 3.1.3?

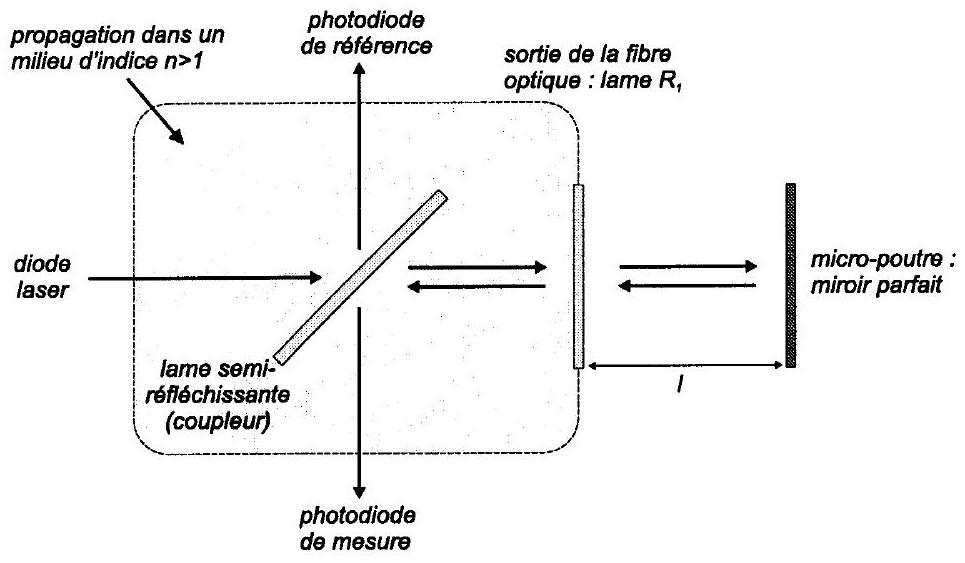
Fig. 5 - Schéma optique équivalent du dispositif interférométrique utilisé pour la mesure de la force de Casimir entre deux plans.

3.2 Capteur interférométrique

Le faisceau émis par une diode laser (longueur d'onde moyenne dans le vide

) est envoyé à travers une fibre optique (d'indice optique

) sur un coupleur directionnel qui est l'équivalent d'une lame semi-réfléchissante pour des faisceaux se propageant dans des fibres. Le faisceau est alors séparé en deux faisceaux de même intensité : l'un est envoyé (toujours à travers une fibre) sur une photodiode (photodiode de référence) qui mesure son intensité, le second est envoyé dans la fibre optique de mesure. À la sortie de cette fibre, une fraction

de l'intensité du faisceau est réfléchie directement dans la fibre. La partie transmise se propage dans l'air (d'indice optique unité), se réfléchit sur la surface réfléchissante de la micro-poutre, considérée comme un miroir parfait, et repart dans la fibre optique. Le signal d'interférence est détecté sur une photodiode (photodiode de mesure). On négligera d'éventuelles réflexions multiples entre la sortie de la fibre et la surface de la micro-poutre.

Montrer que l'intensité détectée se met sous la forme :

où

est la distance entre l'extrémité de la fibre et la micro-poutre, et

la visibilité des franges dont on donnera l'expression simplifiée dans la limite

.
2. (a) Représenter l'allure de

en fonction de

.
(b) Montrer que ce montage permet de détecter de très petites variations de

. A quelle plage de variation est-on par contre limité?
(c) À quel point de fonctionnement

doit-on se placer afin d'avoir le maximum de sensibilité sur un éventuel déplacement

(tel que

)? On suppose dans la suite que cette condition est remplie.
3. En l'absence de tout déplacement, on constate des fluctuations du signal de sortie, dont l'amplitude dépend linéairement de la distance

entre l'extrémité de la fibre et la surface réfléchissante.
(a) À quoi cela peut-il être lié? Montrer que cet effet peut limiter la sensibilité

de l'interféromètre, c'est-à-dire le plus petit déplacement qu'il permet de mesurer.
(b) Expérimentalement, la sensibilité

est de l'ordre de quelques angströms pour un écartement

de l'ordre de quelques dizaines de microns. Que peut-on en conclure sur la source laser utilisée?
(c) Pour minimiser cet effet, on a intérêt à prendre

le plus petit possible. Voyez-vous une analogie avec une expérience effectuée en travaux pratiques?
4. A quoi peut servir la photodiode de référence?

4 Expérience de Mohideen

Pour s'affranchir des contraintes liées au parallélisme entre les deux surfaces planes, l'équipe d'Umar Mohideen a mesuré dès 1997 la force de Casimir entre un plan métallique et une sphère de polystyrène (rayon

) métallisée et collée à l'extrémité d'une micro-poutre triangulaire de

. L'expérience est réalisée à température ambiante

Fig. 6 - Vue au microscope électronique de la sphère de polystyrène collée à l'extrémité d'une micro-poutre, utilisée dans l'expérience de Mohideen, reproduite de l'article original.

4.1 Calcul de la force dans une géométrie plan-sphère

Dans cette géométrie, représentée sur la figure 7 , on admettra que l'on peut sommer les forces sur des surfaces élémentaires de la sphère, même si elles ne sont pas parallèles au plan conducteur, avec une distance locale

qui varie avec l'angle de la surface annulaire considérée.

Donner l'expression de .
En sommant sur la demi-sphère en regard du plan métallique, montrer que dans cette configuration et dans la limite , le module de la force se met sous la forme :

En déduire l'énergie d'interaction dont dérive cette force.

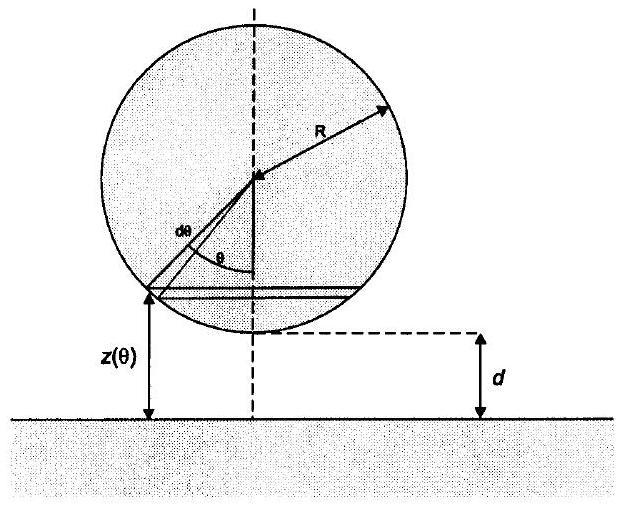
Fig. 7 - Géométrie plan-sphère utilisée dans l'expérience de Mohideen, et notations utilisées pour le calcul de la force de Casimir dans cette configuration.

4.2 Principe de la mesure de force

Dans cette expérience, on mesure directement la force à travers la déflexion statique de la micropoutre. On peut montrer que pour le régime de force considéré, le déplacement vertical de l'extrémité de la micro-poutre (supposée indéformable) est proportionnel à la force appliquée, et on notera

(

étant homogène à une constante de raideur) le coefficient de proportionnalité. La déflexion statique est mesurée grâce à la déviation d'un faisceau laser, qui se réfléchit sur la micro-poutre avant d'être détecté sur une photodiode à quadrants, c'est-à-dire un ensemble de deux photodiodes accolées et de mêmes caractéristiques. Le signal expérimental est la différence des intensités détectées sur les deux quadrants.
Quand le plan conducteur est à grande distance de la sphère, la micro-poutre est horizontale, le faisceau laser incident avec un angle de

et la photodiode à quadrants centrée sur le faisceau réfléchi de façon à annuler le signal. On néglige les effets liés à la taille finie de la photodiode et suppose que chacun des quadrants couvre un demi-plan.

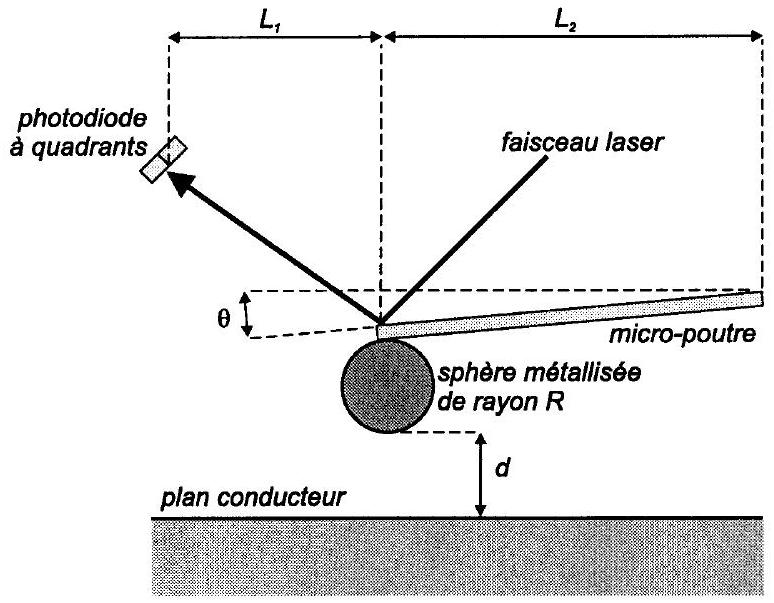
Fig. 8 - Schéma du dispositif expérimental utilisé par Mohideen (pas à l'échelle).

Le faisceau laser a une distribution transverse d'intensité gaussienne, c'est-à-dire qu'à une distance

de l'axe du faisceau, l'intensité surfacique est de la forme :

où

est l'intensité totale du faisceau et

sa taille caractéristique, appelée waist, au niveau de la photodiode à quadrants.

Relier le déplacement vertical de l'extrémité de la micro-poutre à l'angle que fait la micro-poutre avec sa position en l'absence de force appliquée.
Exprimer le signal expérimental en fonction de l'angle . On ne tient compte dans ce calcul que de la variation d'orientation de la micro-poutre et on suppose donc que le point d'impact du faisceau sur la micro-poutre reste fixe.
Donner l'allure des variations du signal avec l'angle .
À quelle condition le signal détecté dépend-il linéairement de la force appliquée à la micropoutre?

4.3 Calibration

Pour calibrer la mesure de force, c'est-à-dire relier le déplacement mesuré à la force appliquée, on utilise une calibration électrostatique, en mesurant directement la force subie par les armatures quand elles sont placées à des potentiels électrostatiques différents.

Montrer que la force exercée entre le plan et la sphère chargés est proportionnelle à , où et sont les potentiels électrostatiques de la sphère et du plan. En pratique, la sphère est mise au potentiel de la terre : .
Proposer succintement une procédure de calibration.
La procédure fournit comme valeur pour la constante de raideur : . Vérifier que le mouvement d'agitation thermique ne modifie la valeur de la force de Casimir qu'à un niveau inférieur à un pour cent.

4.4 Résultats expérimentaux

Le tableau suivant fournit quelques résultats expérimentaux, adaptés de l'article de Mohideen (Physical Review A 62, 052109). Pour chaque distance

, le résultat fourni est la valeur moyenne de la force sur 25 mesures indépendantes.


70
100
150
200
300

Comment est-il adapté de représenter les résultats expérimentaux pour vérifier la loi établie dans la section 4.1?
Effectuer cette représentation graphique.
Pour le point , comment devrait-on représenter l'incertitude expérimentale, sachant que les 25 mesures sont caractérisées par un écart-type de ?
Conclure.

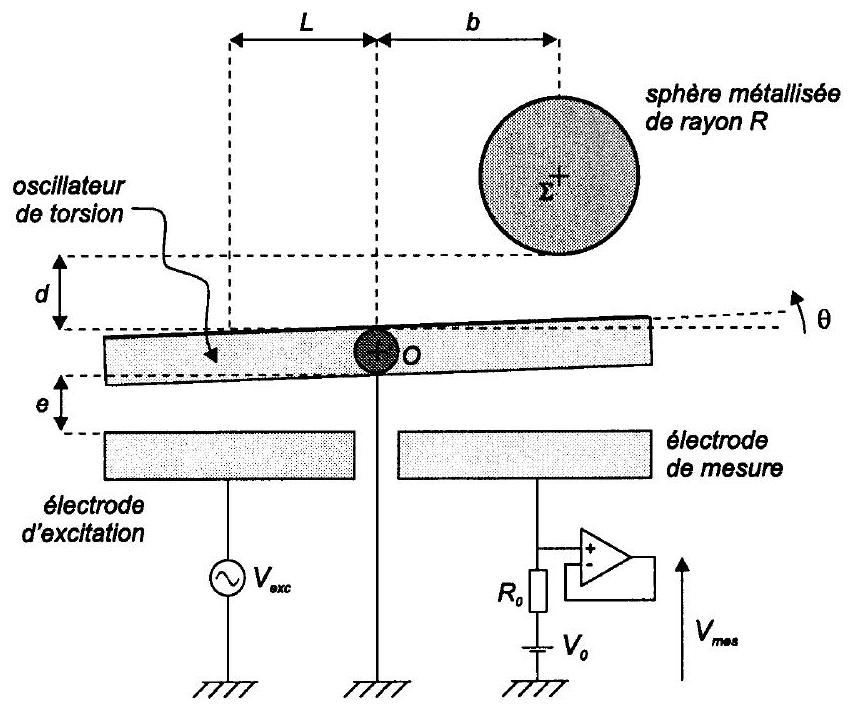
Fig. 9 - Schéma du dispositif expérimental utilisé par Capasso (pas à l'échelle).

5 Expérience de Capasso

Les progrès effectués en micro-mécanique ont permis de réaliser des capteurs ayant des dimensions de l'ordre du micron et en-dessous, qui sont par exemple utilisés dans les dispositifs intégrés qui déclenchent les airbags. De nouveaux progrès permettraient d'aborder un domaine où la force de Casimir est susceptible de modifier sensiblement le comportement mécanique du capteur. C'est pour mettre en évidence de tels effets que l'équipe de Federico Capasso a réalisé en 2001 un oscillateur ad hoc, constitué d'un micro-oscillateur de torsion en silicium métallisé, positionné à proximité d'une sphère semblable à celle utilisée dans l'expérience de Mohideen.

Le dispositif expérimental est représenté sur la figure 9. Un oscillateur de torsion métallisé (et mis au potentiel de la terre) est placé en regard de deux autres électrodes qui sont utilisées pour exciter son mouvement angulaire (électrode d'excitation) ou détecter celui-ci (électrode de mesure). On néglige dans les calculs l'épaisseur de l'oscillateur de torsion.

L'objet de cette partie est l'étude de l'influence de la force de Casimir exercée par la sphère sur la réponse de l'oscillateur à une force extérieure.

5.1 Détection du mouvement

L'oscillateur de torsion est mis à la masse. La variation de capacité du condensateur formé par l'électrode de mesure et le demi-oscillateur en regard est mesurée à l'aide d'un montage électronique simple utilisant un amplificateur opérationnel qu'on supposera parfait.

Montrer que pour de petits angles de déviation, la variation de la capacité du condensateur dépend linéairement de l'angle . Donner l'expression de dans cette approximation. On note la capacité obtenue pour et la distance entre l'axe de rotation et celui du condensateur.
On pose , où est la tension continue mesurée à la sortie du montage en l'absence de mouvement de l'oscillateur. On suppose .
(a) Écrire l'équation électrique du système.
(b) La linéariser. En déduire .
(c) Montrer que la tension est solution de :

(d) Donner

quand

oscille à une pulsation

et en déduire à quelle condition sur les paramètres la tension de sortie reflète fidèlement le mouvement de l'oscillateur.

5.2 Excitation du mouvement

Quelle force subit l'oscillateur si on applique à l'électrode d'excitation une tension , où est une tension continue et une tension alternative?
Quelle relation doit-il y avoir entre et pour exciter le mouvement à une seule fréquence?
On note la force appliquée au résonateur grâce à cette électrode. On s'intéresse dans la suite à la réponse de l'oscillateur à une force appliquée grâce à l'électrode d'excitation, en présence de la sphère qui exerce une force .

5.3 Réponse linéaire

L'oscillateur a un moment d'inertie

. Il est relié à un fil de torsion qui exerce un couple de rappel (avec une constante de torsion

) et il subit également un couple de frottement visqueux

(avec

). On suppose dans la suite que l'oscillateur a sa position d'équilibre en

quand on applique uniquement une force

non nulle.
La sphère a un rayon

et elle est placée à une distance

de l'axe de rotation de l'oscillateur de torsion. La distance

varie de 100 nm à quelques microns.

En développant , montrer que sous l'action de la force , l'équation régissant les petits mouvements de l'oscillateur autour de sa position d'équilibre est de la forme :

où

est une pulsation et

un couple dont on donnera l'expression.
2. Application numérique : calculer

successivement pour une distance d'approche

et de 100 nm .
3. Calculer l'amplitude complexe

de la réponse angulaire en fonction de la fréquence de l'excitation

. Montrer qu'au voisinage de la résonance :

où

est le désaccord.
4. Représenter l'allure de la réponse en fréquence de l'oscillateur.

5.4 Réponse non linéaire

On cherche à déterminer l'équation du mouvement de l'oscillateur au troisième ordre en

(a) En introduisant l'angle entre l'horizontale et la droite , montrer que la distance entre le plan et la sphère est égale à :

(b) Développer

au troisième ordre en

. Evaluer l'ordre de grandeur des différents termes pour une amplitude d'oscillation

rad et une distance

de 100 nm . Justifier qu'il suffit de prendre

pour obtenir l'équation du mouvement au troisième ordre en

.
2. En poursuivant le développement de

, montrer que dans les mêmes conditions que précédemment, cette équation se met sous la forme :

où

sont des constantes qu'on exprimera en fonction des dérivées spatiales de

.
3. On cherche à déterminer la fréquence propre de l'oscillateur et la forme de ses oscillations libres. Pour cela, on néglige dans cette partie son amortissement et on cherche des solutions sous la forme :

avec

et une fréquence

de la forme :

(a) En reportant (16) et (17) dans l'équation du mouvement libre, déterminer les coefficients

, et montrer que :

(b) Est-il étonnant de trouver une valeur moyenne non nulle pour le déplacement?
4. On cherche maintenant à déterminer le profil de la réponse en fréquence de l'oscillateur non linéaire.
(a) Evaluer le coefficient

pour une distance d'approche de la sphère d'une centaine de nm et montrer qu'il est négatif.
(b) En supposant que l'équation (13) est toujours valable, justifier qu'au voisinage de la résonance, l'amplitude de la réponse angulaire est solution de :

5.5 Résultats expérimentaux

Commenter les courbes de résonance obtenues expérimentalement par Capasso, et notamment :

l'ordre de grandeur de l'amplitude des oscillations observées,
le fait que la fréquence de résonance diminue quand on approche la sphère,
le fait que la courbe de réponse, initialement symétrique, se déforme quand les non linéarités augmentent,
le comportement bistable de l'oscillateur, observé sur les deux dernières courbes expérimentales.

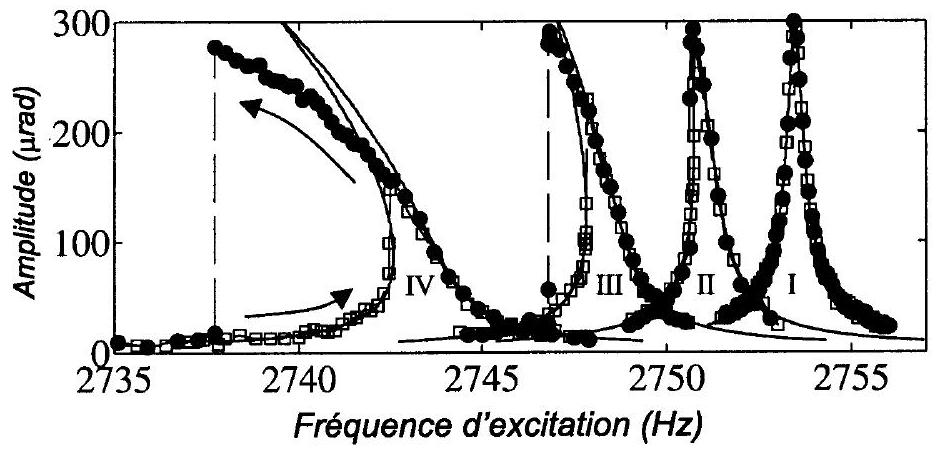
Fig. 10 - Courbes expérimentales obtenues par Capasso, reproduites de Physical Review Letters

. L'amplitude d'excitation est maintenue constante. Les résultats expérimentaux correspondent à une distance

d'approche de la sphère décroissante :

et 98 nm pour les courbes I à IV. Les carrés vides correspondent aux mesures effectuées en augmentant la fréquence d'excitation, les cercles pleins à celles effectuées en la diminuant. Les courbes en traits pleins correspondent à un ajustement des résultats expérimentaux par l'équation (19).