J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

ENS Physique PC 2002

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ens
🔗 Explorer
Banque
X-ENS
Année
2002
Filière
PC
Matière
Physique
X-ENS PCX-ENS 2002PC PhysiquePhysique 2002
2025_09_04_0b29053e9cfdd222b509g
Les correcteurs accorderont une importance particulière à la rigueur des raisonnements et aux représentations graphiques demandées.
Ce sujet aborde le phénomène d'instabilité dans des systèmes dynamiques à deux degrés de liberté couplés. Il se compose de trois parties pouvant être largement traitées de manière indépendante. Dans la première partie, les effets de couplages passif et réactif sont étudiés dans le cas de circuits électriques. La seconde et la troisième partie ont pour objet l'étude des mouvements de la travée centrale d'un pont suspendu, en absence puis en présence d'un vent régulier.

1 Instabilités dans les systèmes dynamiques à deux degrés de liberté couplés : exemples électriques

1.1 Cas d'un couplage passif symétrique

On considère le circuit électrique couplé de la Figure 1.
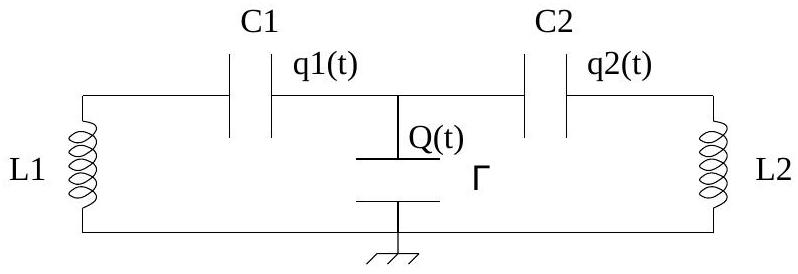
Fig. 1 - Schéma du circuit électrique couplé.
A l'instant initial, .
  1. Etablir les équations qui régissent la dynamique des charges et portées par les armatures droites des condensateurs et .
On s'intéresse désormais aux modes propres d'oscillation, c'est à dire à des solutions complexes de la forme
  1. Montrer que les modes propres des circuits découplés, représentés sur la Figure 2, sont périodiques et donner les expressions des pulsations propres et associées.
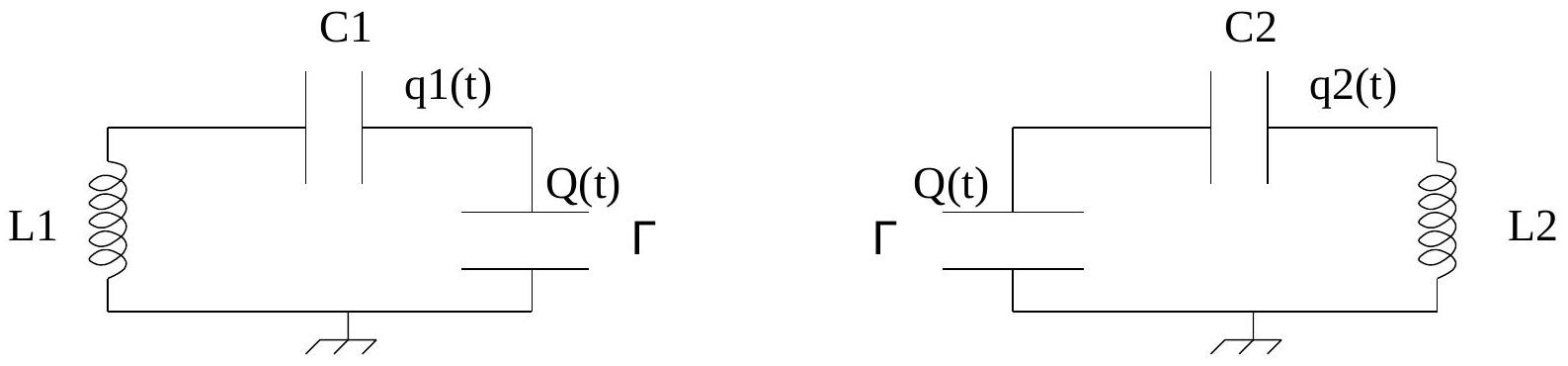
Fig. 2 - Schéma des circuits électriques découplés. A l'instant initial, et respectivement.
On introduit le coefficient de couplage passif défini par l'équation
  1. Montrer que .
  2. Exprimer en fonction de et l'équation satisfaite par les modes propres du circuit couplé.
  3. Représenter graphiquement pour réel et montrer que les modes propres du circuit couplé sont périodiques.
On note et les pulsations propres du circuit couplé.
6) Etablir que le couplage écarte les pulsations propres, c'est à dire que
en convenant que .

1.2 Couplage réactif asymétrique

On considère le circuit électrique de la Figure 3.
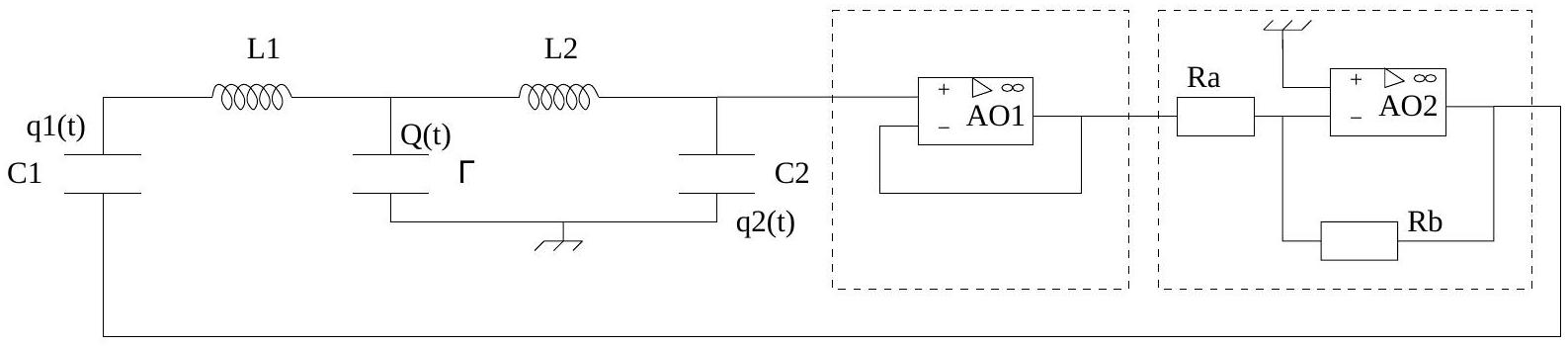
Fig. 3 - Schéma du circuit électrique avec couplage réactif.
A l'instant initial, .
Les amplificateurs opérationnels AO1 et AO2 sont supposés idéaux et fonctionnant en régime linéaire. Les caractéristiques d'un amplificateur opérationnel idéal fonctionnant en régime linéaire sont rappelées sur la Figure 4.
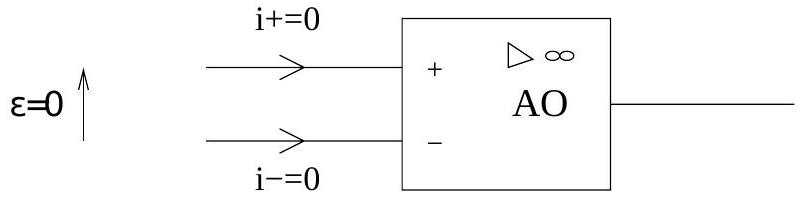
Fig. 4 - Caractéristiques d'un amplificateur opérationnel idéal fonctionnant en régime linéaire. Les courants d'entrée et sont nuls. La différence de potentiel entre les bornes d'entrée + et - est nulle.
  1. Quelles sont les fonctions respectives des éléments de circuit (encadrés) impliquant les amplificateurs opérationnels AO1 et AO2?
On introduit le coefficient de couplage réactif
  1. Déterminer, en fonction de défini par l'équation (1), et l'équation en satisfaite par les modes propres du circuit.
  2. Représenter graphiquement dans le plan complexe (Figure 5) les trajectoires des solutions de l'équation précédente lorsque le coefficient de couplage réactif croît, c'est à dire lorsque l'on augmente le rapport des deux résistances.
Fig. 5 - Plan complexe de .
  1. A partir du graphique de la question précédente, déduire qu'il existe une valeur critique du coefficient de couplage réactif, que l'on explicitera en fonction de , et , pour laquelle les deux pulsations propres du circuit se confondent, et que si l'on pousse au delà ce couplage les oscillations propres du système se font à une fréquence unique, mais avec des amplitudes pouvant diverger exponentiellement avec le temps. On se contentera pour ce dernier point d'une justification qualitative.

2 Modes propres d'oscillation verticale de la travée centrale d'un pont suspendu

2.1 Etude de l'équilibre mécanique

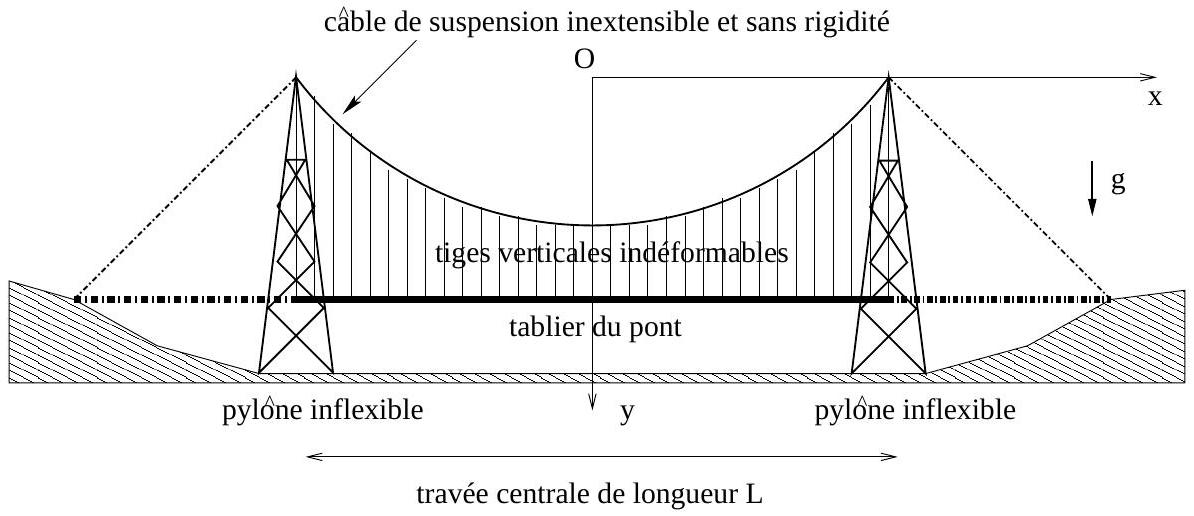
Fig. 6 - Schéma du pont suspendu à l'équilibre. La structure du pont est symétrique par rapport à l'axe Oy. Le pont est soumis à la gravité terrestre de constante . Le référentiel , associé au repère d'espace cartésien Oxy, est supposé Galiléen.
La travée centrale du pont, c'est à dire la partie du tablier (dalle porteuse du pont) comprise entre les deux pylônes, est suspendue au câble de suspension par des tiges verticales indéformables régulièrement espacées (Figure 6). Les extrémités de la travée centrale sont fixées aux pylônes.
Le câble de suspension est supposé inextensible et sans rigidité. L'absence de rigidité signifie que, non tendu, le câble peut être déformé par une action négligeable. Le câble de suspension est attaché à ses extrémités aux sommets des deux pylônes considérés inflexibles. La longueur des tiges est telle qu'à l'équilibre, la travée centrale du pont est parfaitement horizontale, sans contrainte mécanique interne.
On suppose que la masse du tablier du pont est uniformément répartie. Les masses (non nulles) du câble de suspension et des tiges verticales seront négligées devant la masse du tablier.
On note la forme du câble à l'équilibre dans le repère cartésien . On suppose que l'on peut négliger la courbure du câble sur la distance qui sépare deux tiges verticales successives.
11) En écrivant, en coordonnées cartésiennes, que la résultante des forces qui s'exercent sur un élément infinitésimal du câble, de longueur de l'ordre de la distance entre tiges verticales, est nulle, établir que la dérivée seconde de par rapport à est constante le long du câble.
12) Déduire que
Le coefficient est appelé la flèche du câble.
Soit l'amplitude de la force horizontale de retenue du câble aux sommets des pylônes.
13) Montrer que
où désigne la masse linéique (par unité de longueur) du tablier, est l'accélération gravitationnelle.

2.2 Equations dynamiques des oscillations verticales de la travée centrale

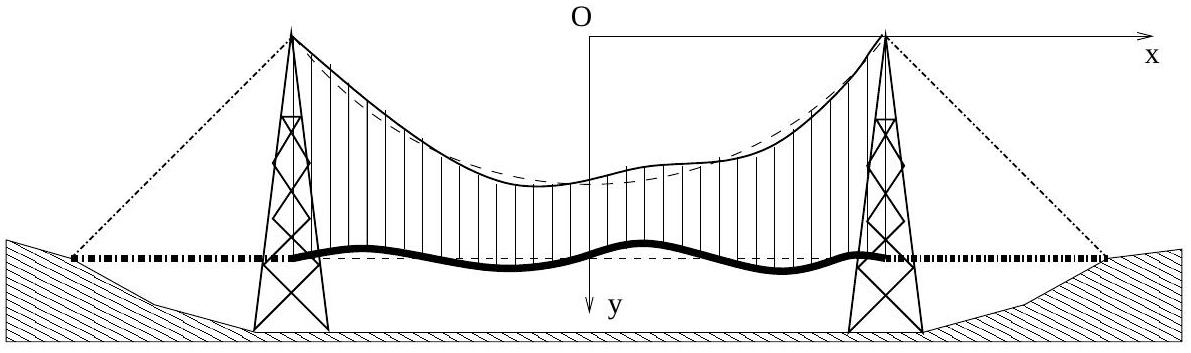
Fig. 7 - Schéma du pont suspendu en oscillation.
On considère maintenant que la travée centrale du pont, et par conséquent le câble de suspension, sont en mouvement d'oscillation verticale (Figure 7). On néglige les mouvements horizontaux du câble et de la travée centrale du pont. On désigne par la déformation verticale du câble par rapport à sa position d'équilibre, c'est à dire que la forme du câble est désormais donnée par . Enfin, on se place dans le cadre de petites oscillations régulières qui modifient peu la courbure du câble de suspension.
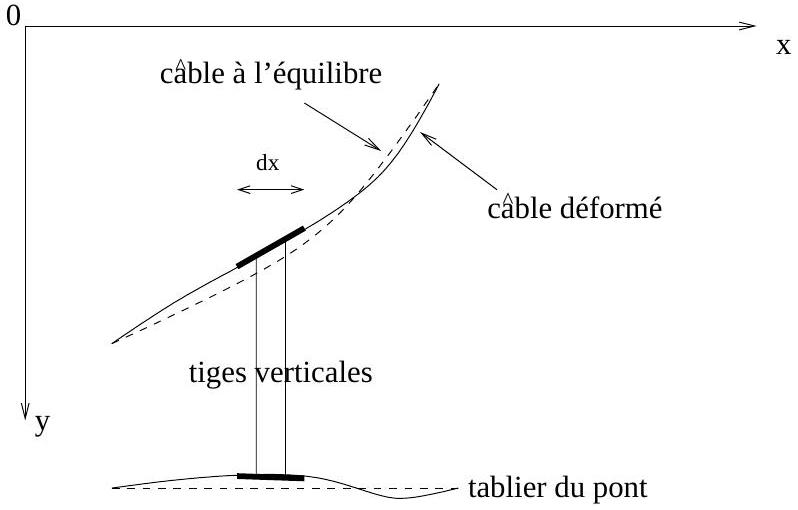
Du fait de l'inertie des mouvements du tablier du pont, le câble de suspension supporte une charge variable verticale supplémentaire par unité de longueur suivant , par rapport à la situation d'équilibre, notée . La force horizontale de retenue du câble au sommet des pylônes a maintenant pour amplitude .
Fig. 8 - Schéma de la déformation du câble et du tablier.
  1. Appliquer la relation fondamentale de la dynamique à un élément de câble de largeur dans le référentiel (Figure 8), et établir une première équation dynamique reliant et .
On suppose qu'un élément du tablier du pont de largeur n'est soumis à aucune autre force à composante verticale que son propre poids et la force de traction des tiges. On néglige donc la rigidité du tablier.
15) Dans le référentiel , appliquer la relation fondamentale de la dynamique à l'élément du tablier du pont correspondant à l'élément du câble de la question précédente, et établir une seconde relation entre et .
16) Eliminer dans le système d'équations précédent. En déduire l'équation différentielle satisfaite par la déformation :

2.3 Modes propres d'oscillation verticale

On s'intéresse aux modes propres d'oscillation, c'est à dire aux ondes stationnaires de déformation qui peuvent s'établir à certaines fréquences d'oscillation. Dans ce cadre, on cherche des solutions sous la forme
  1. Montrer que pour une telle solution , où est une constante.
On utilise dans la suite le paramètre défini par
  1. Quelle est la dimension de ?
  2. Etablir l'équation différentielle satisfaite par et donner l'expression de la solution générale de cette équation.
  3. En supposant que la flèche du câble est petite devant la longueur de la travée centrale du pont, montrer que l'inextensibilité du câble impose la condition
On considère tout d'abord les modes symétriques pour lesquels la fonction vérifie .
21) Donner l'expression analytique des modes symétriques.
22) Montrer que les pulsations propres des modes symétriques sont solutions de l'équation transcendante
  1. Représenter graphiquement, l'allure des deux premiers modes symétriques.
  2. Comparer la période propre du mode symétrique de plus basse fréquence à la période d'un pendule simple de longueur en régime de petites oscillations.
On s'intéresse maintenant aux modes anti-symétriques, pour lesquels la fonction vérifie .
25) Montrer que pour les modes anti-symétriques . Analyser simplement ce résultat par un argument physique.
26) Donner l'expression analytique des modes anti-symétriques, en précisant les pulsations propres.
27) Représenter graphiquement, l'allure des deux premiers modes anti-symétriques.

3 Oscillations de flexion et torsion de la travée centrale d'un pont suspendu sous l'action d'un vent régulier

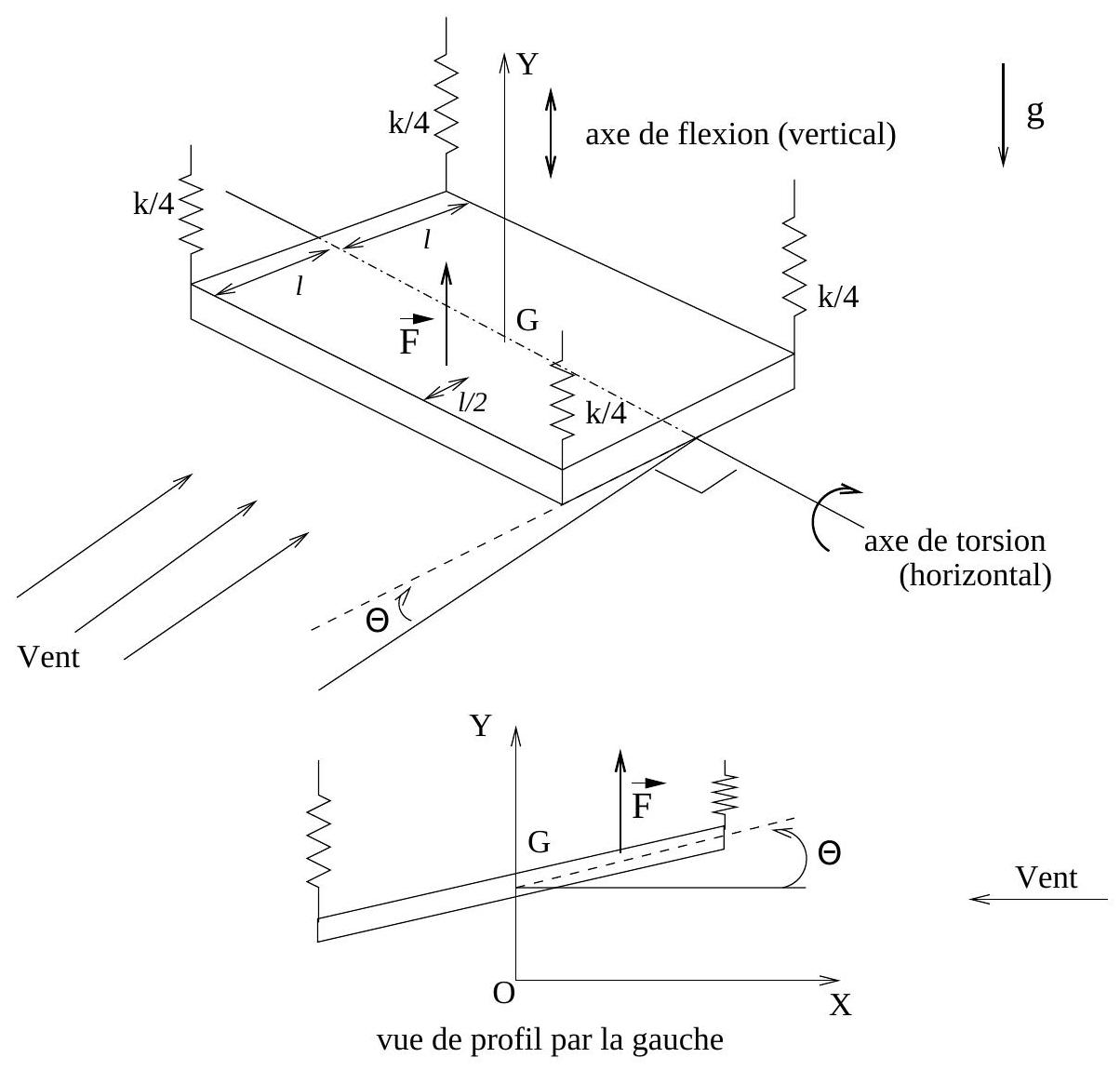
Fig. 9 - Modèle mécanique d'un élément de la travée centrale d'un pont suspendu soumis à l'action d'un vent régulier.
On s'intéresse à un élément de la travée centrale du pont. L'étude précédente nous permet de modéliser l'action du reste de la travée et du câble de suspension, sur cet élément, par une force élastique de rappel verticale. On considère par ailleurs un degré de liberté de mouvement supplémentaire; la torsion du tablier.
On modélise ainsi un élément de la travée centrale par une plaque homogène de masse , de profondeur dans le sens du vent et d'épaisseur négligeable, soutenue par quatre ressorts verticaux de même raideur fixés aux quatres coins (Figure 9). Les extrémités supérieures des ressorts sont fixes.
Sous l'effet du vent, de vitesse , cette plaque est soumise à un mouvement de flexion, repéré par le déplacement vertical de son centre de gravité , et de torsion, repéré par l'angle de rotation . A l'équilibre, lorsque la vitesse du vent est nulle, la plaque est horizontale : et .
On se place dans l'approximation des petits mouvements de flexion et torsion, c'est à dire que et restent très petits devant 1 .
On désigne par le moment d'inertie de la plaque par rapport à son axe de symétrie perpendiculaire au vent (axe de torsion). La force verticale désigne la résultante des forces de portance du vent sur le pont. On admet que cette force résultante s'applique à la distance du bord d'attaque du vent (Figure 9 ).
28) En absence de vent, établir l'expression de la pulsation d'oscillation verticale de la plaque en fonction de et .
29) En identifiant cette pulsation à la pulsation propre des modes d'oscillation étudiés dans la partie précédente, établir une relation entre et .
On cherche maintenant à établir les équations qui régissent la dynamique des variables et .
30) Appliquer la relation fondamentale de la dynamique à la plaque en mouvement dans le référentiel Galiléen , associé au repère d'espace cartésien , et établir l'équation satisfaite par .
31) Appliquer le théorème du moment cinétique à la plaque dans le référentiel et établir l'équation satisfaite par .
On admet dans ce qui suit que la composante de la résultante des forces de portance du vent, qui couple les variables et , a pour expression
où est une constante positive.
On étudie d'abord séparément les mouvements de flexion et torsion.
32) Décrire le mouvement de flexion ( ). Est-il stable?
33) Montrer qu'il existe une vitesse critique du vent, que l'on explicitera, au dessus de laquelle le mouvement de torsion devient instable.
On s'intéresse maintenant au mouvement géneral de flexion et torsion couplées, décrit par les équations obtenues précédemment. On cherche des solutions sous la forme de modes propres
On introduit les pulsations caractéristiques
  1. Déterminer l'équation du quatrième degré satisfaite par .
On réécrit cette équation sous la forme
On peut montrer qu'une condition nécessaire pour que toutes les racines (complexes) de cette équation du quatrième degré aient une partie réelle négative s'écrit
  1. Déduire de la troisième condition que les ponts suspendus, dans le cadre de ce modèle, sont fondamentalement instables dans le vent par suite du couplage entre flexion et torsion induit par les forces de portance aérodynamiques.
Ce résultat permet de comprendre l'instabilité des premiers grands ponts suspendus en présence de vent régulier.
Fig. 10 - Photographie de l'instabilité qui a conduit à la destruction du pont de Tacoma le 7 Novembre 1940.
ENS Physique PC 2002 - Version Web LaTeX | WikiPrépa | WikiPrépa