Version interactive avec LaTeX compilé
SESSION 2003
Filière MP
PHYSIQUE
Épreuve commune aux ENS de Lyon et Cachan
Durée : 4 heures
L'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé. Cependant, une seule calculatrice à la fois est admise sur la table ou le poste de travail, et aucun échange n'est autorisé entre les candidats.
Les correcteurs accorderont une importance particulière à la clarté et à la précision des raisonnements.
Le problème de l'adhérence de deux solides en contact adhésif, c'est-à-dire collés l'un sur l'autre, serait plus simple si les solides étaient indéformables, auquel cas la distension et la rupture des seules liaisons d'adhésion seraient à prendre en compte lors de la séparation. En réalité, la séparation ne se fait pas d'un bloc mais par réduction progressive de l'aire de contact et elle s'accompagne d'une déformation élastique des solides.
Nous étudions dans ce problème la thermodynamique du phénomène de rupture du contact entre deux solides. Le formalisme thermodynamique est abordé dans la première partie. Dans la seconde partie, les états d'équilibre thermodynamique du système sont étudiés et le concept de rupture contrôlée est introduit. La troisième partie traite un exemple concret de décollement de deux solides.
La quatrième partie présente une méthode de mesure optique de l'épaisseur du contact adhésif entre deux solides transparents. Cette dernière partie peut être traitée de manière indépendante.
1 Formalisme thermodynamique du phénomène de rupture du contact adhésif entre deux solides
Pour décrire le phénomène de rupture du contact entre deux solides, supposé à température constante, il est judicieux de considérer la grandeur thermodynamique
où
- L'énergie libre de Helmholtz est-elle une fonction d'état thermodynamique?
- Enoncer les premier et second principes de la thermodynamique.
- Etablir que lors d'une transformation élémentaire réversible, la variation de l'énergie libre d'Helmholtz est égale au travail reçu par le système:
- Dans le cas d'une transformation élémentaire irréversible, établir que la variation de l'énergie libre d'Helmholtz est strictement inférieure au travail reçu par le système:
Dans notre cas, le système thermodynamique considéré est constitué de deux solides en contact adhésif sur une surface d'aire
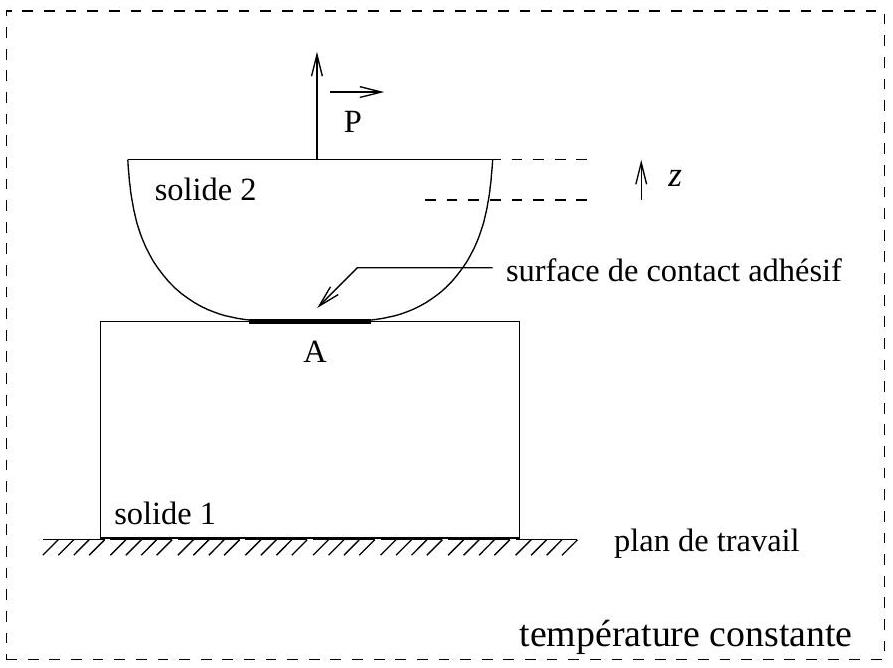
Fig. 1 - Système thermodynamique de deux solides en contact adhésif. Le solide inférieur est fixé au plan de travail supposé immobile.
Au cours d'une transformation élémentaire réversible correspondant à une variation
La constante
5) Quel est le signe de la constante
5) Quel est le signe de la constante
Il faut considérer d'autre part l'énergie potentielle élastique du système, notée
- Qualifieriez-vous la variable thermodynamique
d'intensive ou d'extensive? Préciser votre raisonnement. - Exprimer la variation élémentaire d'énergie potentielle élastique
, relative à une variation de l'aire de contact et une variation du déplacement. - Déduire des questions précédentes que le travail total reçu par le système au cours d'une transformation élémentaire réversible correspondant à une variation
de l'aire de contact et une variation du déplacement, est
Préciser la signification physique des différents termes de cette expression.
2 Etats d'équilibre thermodynamique du système
Dans la pratique, le dispositif expérimental de la figure 2 est utilisé pour étudier l'adhérence de deux solides. La variation de l'aire de la surface de contact s'effectue à déplacement constant
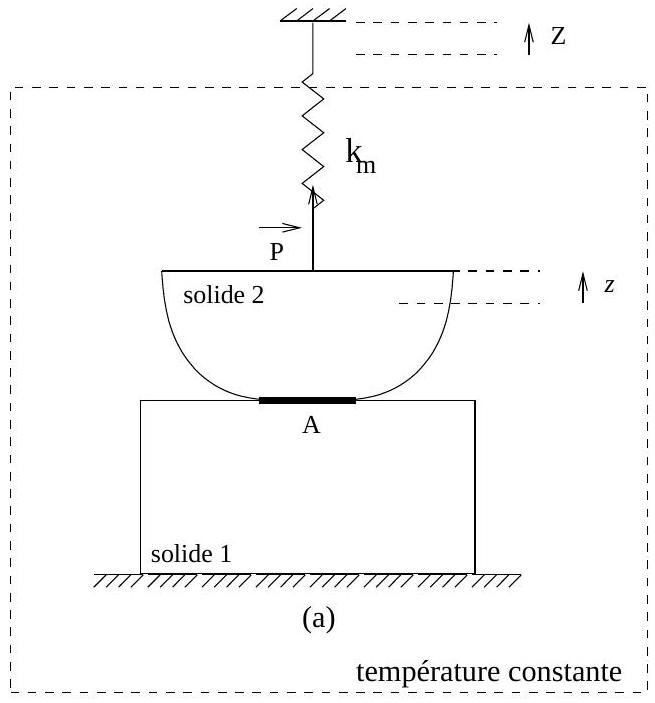
Fig. 2 - Dispositif expérimental de l'étude de l'adhérence, à déplacement constant
- Relier les variables
et . - Dans quelle limite, nulle ou infinie, doit-on prendre la constante de raideur
du ressort pour que le dispositif soit à déplacement constant ? On considérera tout d'abord cette situation dans la suite du problème. - Quel est l'analogue d'une transformation à déplacement constant
en thermodynamique des gaz?
2.1 Conditions d'équilibre thermodynamique
On impose un déplacement constant
12) L'évolution spontanée du système vers son état d'équilibre est-elle réversible? Justifier alors que l'énergie libre de Helmholtz décroît au cours de cette évolution.
13) En déduire que
14) Au cours de l'évolution spontanée du système que se passe-t-il lorsque
15) En déduire qu'à l'équilibre thermodynamique, on a nécessairement
12) L'évolution spontanée du système vers son état d'équilibre est-elle réversible? Justifier alors que l'énergie libre de Helmholtz décroît au cours de cette évolution.
13) En déduire que
14) Au cours de l'évolution spontanée du système que se passe-t-il lorsque
15) En déduire qu'à l'équilibre thermodynamique, on a nécessairement
Cette condition s'appelle le critère de Griffith.
Un état qui satisfait le critère de Griffith n'est pas forcément un état d'équilibre thermodynamique.
16) Montrer qu'il s'agit d'un état d'équilibre thermodynamique si la condition supplémentaire
16) Montrer qu'il s'agit d'un état d'équilibre thermodynamique si la condition supplémentaire
est vérifiée.
On considère désormais que la raideur
17) Etablir que le travail reçu par le système constitué des deux solides en contact et du ressort de traction, au cours d'une transformation élémentaire réversible correspondant à une variation
On considère désormais que la raideur
17) Etablir que le travail reçu par le système constitué des deux solides en contact et du ressort de traction, au cours d'une transformation élémentaire réversible correspondant à une variation
- En considérant le système constitué des deux solides en contact et du ressort de traction, déduire que le critère de Griffith établi précédemment reste valable lorsque le système évolue à déplacement constant
. - Montrer que le critère de Griffith définit un état d'équilibre thermodynamique si la condition supplémentaire
est vérifiée.
20) Démontrer que
20) Démontrer que
- Quelle est la signification du terme
? Quel est son signe?
2.2 Concept de rupture contrôlée
On parle de rupture contrôlée lorsqu'en augmentant très lentement, par incréments successifs de très faible amplitude, le déplacement
22) Quelles conditions sur
23) Que se passe t-il lorsque le déplacement imposé atteint une valeur critique telle que
22) Quelles conditions sur
23) Que se passe t-il lorsque le déplacement imposé atteint une valeur critique telle que
3 Exemple de rupture du collage entre deux lamelles de bois
On considère deux lamelles identiques de largeur
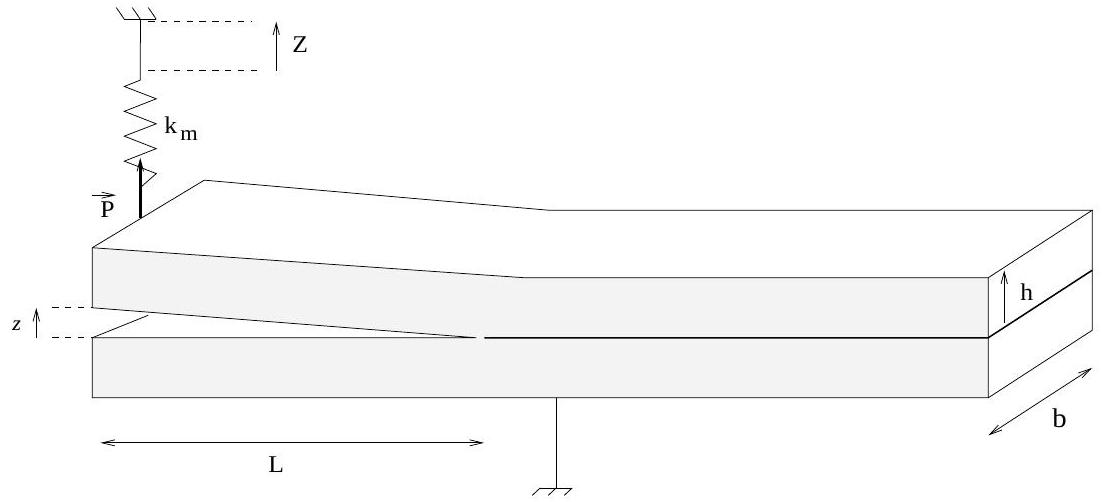
Fig. 3 - Schéma du dispositif de décollement de deux lamelles en contact adhésif.
On admet que l'équation qui relie l'ouverture
24) Etablir que l'énergie potentielle élastique
25) Démontrer que le taux de restitution de l'énergie élastique peut s'écrire
On représente sur la figure 4, l'allure du taux de restitution de l'énergie élastique
26) Quelle est la signification de la longueur critique
27) Etablir la relation que doivent satisfaire
26) Quelle est la signification de la longueur critique
27) Etablir la relation que doivent satisfaire
Considérons deux lamelles de bois de largeur
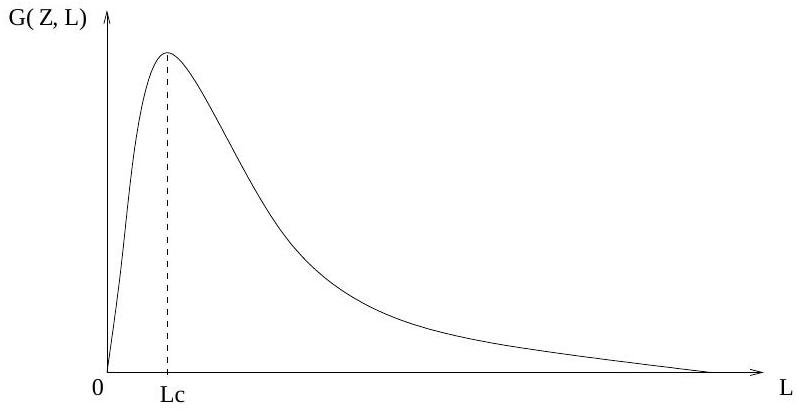
Fig. 4 - Allure du taux de restitution de l'énergie élastique
- Calculer la longueur critique
.
Afin d'amorcer le décollement, on pratique une entaille très fine de longueur
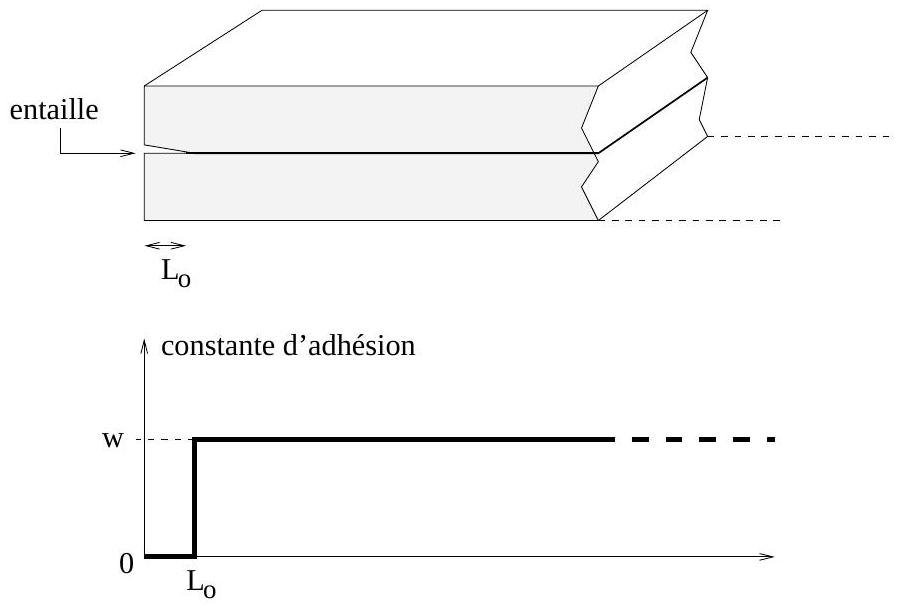
Fig. 5 - Pour amorcer le décollement on pratique une entaille très fine.
On réalise une expérience de rupture en augmentant lentement, par incréments de très faible amplitude, le déplacement imposé
29) Que se passe-t-il au début de l'expérience?
30) Montrer qu'il est nécessaire d'atteindre un déplacement
31) Déterminer
32) Que se passe-t-il lorsque l'on atteint le déplacement
33) Décrire qualitativement, et si besoin illustrer par des courbes et des schémas, la progression du décollement lorsque l'on continue d'augmenter le déplacement
29) Que se passe-t-il au début de l'expérience?
30) Montrer qu'il est nécessaire d'atteindre un déplacement
31) Déterminer
32) Que se passe-t-il lorsque l'on atteint le déplacement
33) Décrire qualitativement, et si besoin illustrer par des courbes et des schémas, la progression du décollement lorsque l'on continue d'augmenter le déplacement
4 Mesure optique de l'épaisseur de la zone de contact adhésif entre deux solides transparents
On suppose que le contact adhésif peut être représenté par un film mince transparent, d'épaisseur

Fig. 6 - Système optique réalisé par deux solides identiques transparents en contact adhésif. Le contact adhésif est représenté par un film mince transparent. On a déposé une fine pellicule d'argent sur les faces externes des deux solides.
Le système est éclairé par la gauche, sous incidence normale, par une onde lumineuse plane monochromatique de longueur d'onde
A l'intérieur du système, l'onde lumineuse se divise par suite de multiples réflexions et transmissions (partielles) sur les surfaces de séparation des trois couches. On étudie l'interférence des ondes émergeant finalement par la droite. On montrera qu'il n'y a interférence constructive entre ces ondes que pour certaines valeurs de la longueur d'onde
34) A quel dispositif optique classique, ce système fait-il penser? Préciser un usage de ce dispositif classique.
34) A quel dispositif optique classique, ce système fait-il penser? Préciser un usage de ce dispositif classique.
A l'interface solide - film adhésif, on désigne par
35) Exprimer les coefficients de réflexion et de transmission (
35) Exprimer les coefficients de réflexion et de transmission (
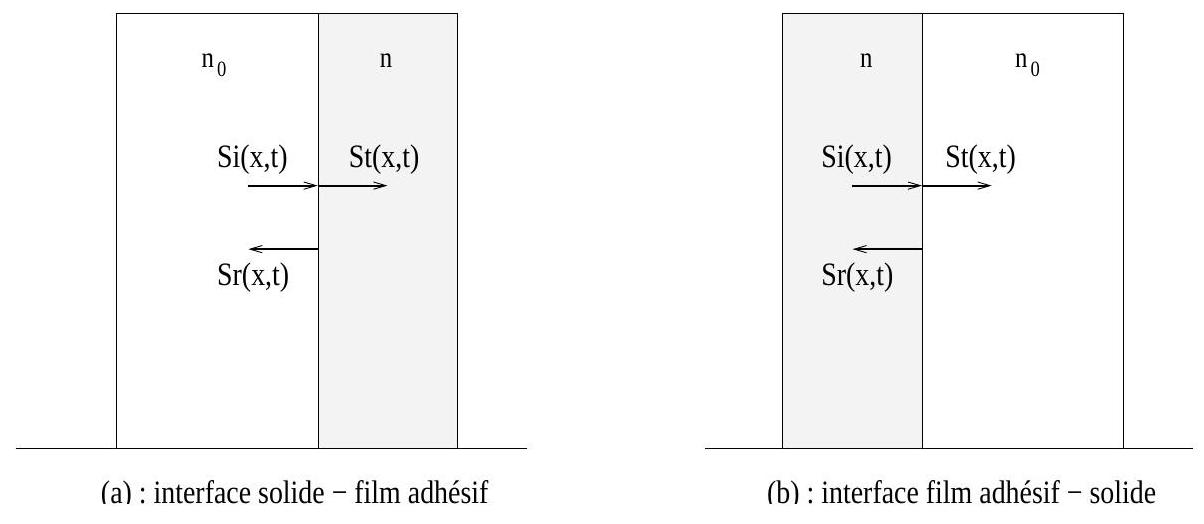
Fig. 7 - Une onde lumineuse incidente
- Vérifier que
Que traduisent ces deux équations?
On suppose que les faces externes des deux solides sont recouvertes d'une fine pellicule d'argent (figure 6). Cette pellicule d'argent réfléchit fortement la lumière et ne transmet qu'une très faible intensité lumineuse. On pourra ainsi considérer, en première approximation, que son facteur de réflexion, défini comme le rapport des intensités de la lumière réfléchie et de la lumière incidente, est égal à 1 . Enfin on négligera les déphasages induits par les réflexions sur les faces argentés.
On suppose que les faces externes des deux solides sont recouvertes d'une fine pellicule d'argent (figure 6). Cette pellicule d'argent réfléchit fortement la lumière et ne transmet qu'une très faible intensité lumineuse. On pourra ainsi considérer, en première approximation, que son facteur de réflexion, défini comme le rapport des intensités de la lumière réfléchie et de la lumière incidente, est égal à 1 . Enfin on négligera les déphasages induits par les réflexions sur les faces argentés.
En raison de la symétrie du système, on peut montrer que la condition d'interférence constructive des ondes lumineuses émergeant du système est équivalente à la condition de résonance suivante:
soit une onde lumineuse d'amplitude unité et de phase nulle issu du plan
soit une onde lumineuse d'amplitude unité et de phase nulle issu du plan
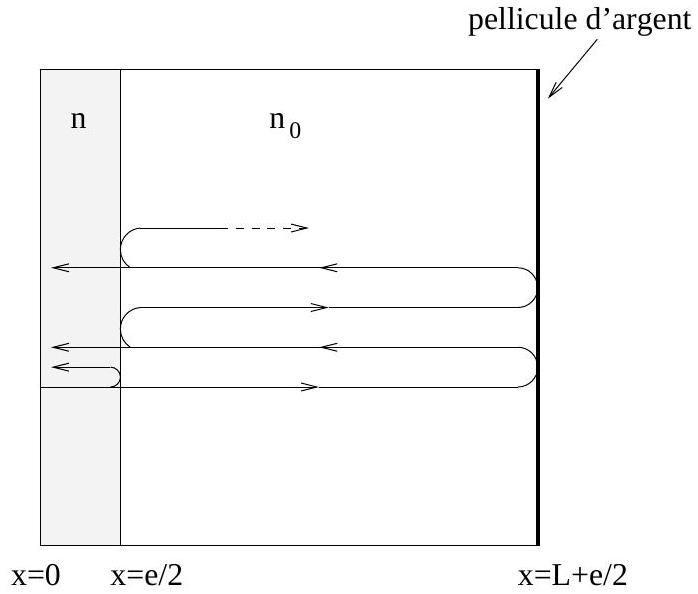
Fig. 8 - En raison de la symétrie du problème, on peut considérer une condition de résonance équivalente.
- Montrer que la condition d'interférence constructive peut s'écrire sous la forme
On s'intéresse tout d'abord au cas où l'épaisseur
38) Etablir qu'il n'y a interférence constructive que pour certaines longueurs d'onde
38) Etablir qu'il n'y a interférence constructive que pour certaines longueurs d'onde
On considère maintenant que l'épaisseur
39) Exprimer le déphasage
39) Exprimer le déphasage
On fait l'hypothèse que l'épaisseur
40) En déduire que la condition d'interférence constructive s'écrit
40) En déduire que la condition d'interférence constructive s'écrit
et
En mesurant le décalage en longueur d'onde, on peut ainsi accéder à l'épaisseur du film adhésif ainsi qu'à son indice de réfraction.
Dans la pratique, cette méthode de mesure est utilisée en éclairant le système interférométrique par une onde plane de lumière blanche. Le spectre du faisceau lumineux émergeant de l'interféromètre est visualisé à l'aide d'un spectrographe imageur à réseau (figure 9). Le spectrographe sépare spatialement les différentes longueurs d'onde du faisceau et fixe l'image du spectre au moyen d'une barrette CCD (Charge Coupled Device qui se traduit en français par Dispositif à Transfert de Charges).
Une barrette CCD est un composant opto-électrique constitué d'une matrice de photoéléments capables de produire des charges électriques sous l'action de la lumière et de les conserver dans un puits de potentiel. La lecture de la charge de chaque photo-élément permet de reconstruire le profil spatial de l'intensité lumineuse éclairant la barrette.
41) Expliquer qualitativement l'image observée au moyen de la barrette CCD du spectrographe.
41) Expliquer qualitativement l'image observée au moyen de la barrette CCD du spectrographe.
On considère deux solides en mica. Lorsque les solides sont en contact non-adhésif trois franges lumineuses successives sont observées, correspondant aux longueurs d'onde
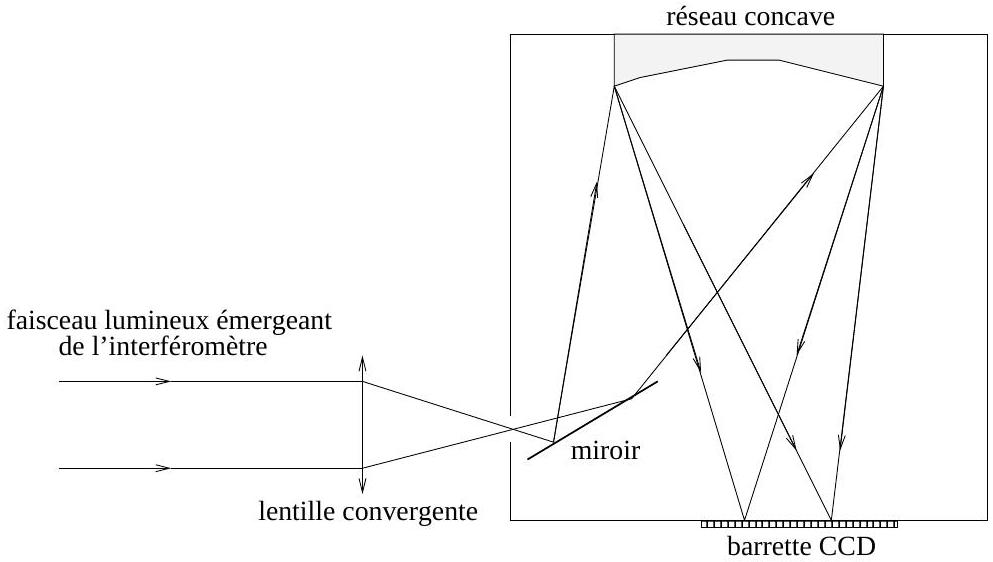
Fig. 9 - Le spectre du faisceau émergeant de l'interféromètre est obtenu à l'aide d'un spectrographe imageur. Le spectre est fixé au moyen d'une barrette CCD.
- Déterminer l'ordre d'interférence
. - Déterminer l'épaisseur
et l'indice de réfraction du film adhésif sachant que l'indice de réfraction pour le mica est . Commenter vos résultats.
FIN DU PROBLEME
