J-0
00m
00j
00h
00min
00s

Version interactive avec LaTeX compilé

Télécharger PDF

ENS Informatique MP PC 2004

Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Logo ens
🔗 Explorer
Banque
X-ENS
Année
2004
Filière
MP/PC
Matière
Info
X-ENS MP/PCX-ENS 2004MP/PC InfoInfo 2004
2025_08_29_60ab060ae3ebae17bda9g

Filière MP (groupes MPI/MI)
Épreuve commune aux ENS de Paris et Cachan

Filière MP (groupe I)Épreuve commune aux ENS de Paris, Lyon et Cachan

Filière PC (groupe I)Épreuve commune aux ENS de Paris et Lyon

INFORMATIQUE

Durée : 4 heures
L'usage de calculatrices électroniques de poche à alimentation autonome, non imprimantes et sans document d'accompagnement, est autorisé. Cependant, une seule calculatrice à la fois est admise sur la table ou le poste de travail, et aucun échange n'est autorisé entre les candidats.
Le problème comporte 13 questions. Il est conseillé de traîter les questions dans l'ordre de l'énoncé, cependant on pourra aborder une question en admettant les résultats des précédentes. Les algorithmes demandés pourront être écrits dans un langage aux choix du candidat, en utilisant les structures de contrôle usuelles. On pourra par exemple utiliser un langage semblable à celui qui est décrit dans l'annexe A.
Un graphe est un triplet ( ) où est un ensemble fini (les sommets), est un sous-ensemble de (les arêtes) et est une application de dans . La taille d'un graphe est la somme du nombre de sommets et du nombre d'arêtes . La taille d'une liste est sa longueur. On pourra supposer que les sommets sont numérotés et donc que . Les éléments de sont de taille 1 .
Si est un ensemble, on note l'ensemble des sous-ensembles de . On pourra choisir de représenter un ensemble d'éléments de par une liste de taille ou par un tableau de booléens de taille .
On utilisera la structure de donnée des tableaux indicés par à valeurs dans un type de donnée (tableaux de en abrégé) qui représentent les applications de dans . On dispose pour de telles données
  • d'une fonction d'accès : est la valeur de en si est un tableau de et . Un tel accès s'effectue en temps unitaire
  • d'une fonction d'initialisation init qui, étant donné , renvoie un tableau représentant la fonction constante égale à . Le coût de cette fonction est .
  • de primitives de modification : modifie le tableau en remplaçant sa valeur en par . Cette opération a un coût unitaire. (Dans un langage fonctionnel, on pourra supposer l'existence d'une fonction de coût unitaire qui renvoie le tableau modifié).
    Le temps nécessaire à l'exécution d'un algorithme sur la donnée sera supposé être le nombre d'opérations élémentaires effectuées : accès à un tableau, test d'égalité sur les données atomiques (éléments de ), test de vide d'une liste, accès au premier élément d'une liste (car), accès au reste d'une liste (cdr), ajout d'un élément à une liste (cons, : :), ajouter ou retrancher 1 à un entier, test à 0 d'un entier, or, and sur des données Booléennes. On utilisera la notation : par exemple, la complexité d'un algorithme est si son temps d'exécution ne dépend pas de la donnée; il est si son temps d'exécution est, dans le cas le pire, linéaire dans la taille de la donnée .

1 Accessibilité dans les graphes ET/OU

Dans cette partie, désignera un graphe . Si est une application de dans , on dira que est compatible avec si, pour tout
  • ou bien et
  • ou bien et

Question 1

Montrer que l'application qui à tout sommet de associe est compatible avec .

Question 2

Montrer que, si et sont deux applications compatibles avec , l'application définie par :
est compatible avec

Question 3

Montrer qu'il existe une unique application compatible avec telle que pour toute application compatible avec et pour tout sommet de
L'application est appelée relation d'accessibilité de . L'objet de cette partie est de construire des algorithmes qui permettent de calculer
On représente les graphes ET/OU à l'aide de deux tableaux G et f indicés par les sommets du graphe : est l'ensemble des sommets de tels que et est égal à .
Les ensembles de sommets seront représentés par des listes sans répétition ou des tableaux de Booléens, au choix du candidat.

Question 4

Donner des algorithmes (ou programmes) qui réalisent les fonctions suivantes :
  1. le test d'appartenance à un ensemble de sommets
  2. le test d'égalité de deux ensembles de sommets
  3. l'union de deux ensembles de sommets
  4. étant donné un ensemble de sommets et un tableau indicé par à valeurs dans les ensembles de sommets, calcule l'union des pour .
  5. étant donné un tableau indicé par , à valeurs dans les ensembles de sommets, et un graphe (donné par G et f ), le test de compatibilité de avec .
    Dans chaque cas, justifier brièvement la correction de l'algorithme et donner sa complexité.

Question 5

On définit la suite d'applications qui associent à chaque sommet un ensemble de sommets :
  • pour tout
  • Si
  • Si
  1. Calculer la suite pour chacun des 9 sommets du graphe donné dans la figure 1 , dans lequel pour les sommets représentés par des cercles et pour les sommets représentés par des carrés.
  2. Montrer que, pour tout graphe , il existe un entier que l'on précisera tel que, pour tout , pour tout . On notera alors la limite ainsi obtenue.
  3. Montrer que
  4. En déduire un algorithme de calcul de dont on précisera la complexité.

Question 6

Si est un ensemble de sommets de , on note (ensemble des sommets desquels on peut accéder à un sommet de ). Donner un algorithme qui, étant donnés et , calcule et préciser sa complexité.

Question 7

On associe à chaque sommet la liste de ses prédecesseurs prec( ) et le nombre qui est égal au nombre de successeurs de si et égal à 1 sinon.
Soient des listes de sommets. Initialement est vide et . On considère l'algorithme donné dans la figure 2.
  1. Montrer que la complexité de cet algorithme est
  2. Montrer que, après éxecution, . (Ind : on pourra montrer que, si , à chaque entrée dans la boucle externe).
  3. Donner un algorithme qui calcule toutes les listes sans répétitions prec et tous les entiers , pour , en temps (total) .
  4. En déduire qu'il existe un algorithme linéaire qui résoud le problème d'accessibilité : étant donnés et , l'algorithme répond true si et false sinon.
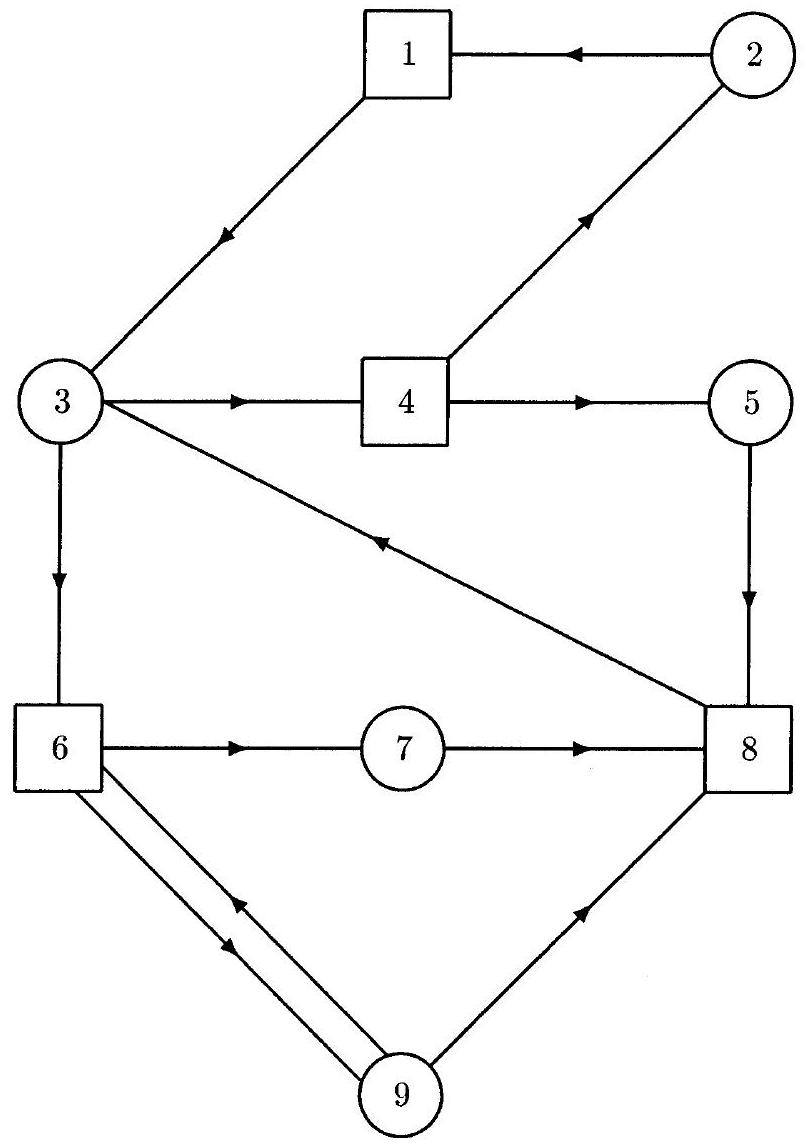
Fig. 1 - Un graphe ET/OU
Pour faire
Tant que non vide faire
Tant que non vide faire
Fin Tq
Fin Tq
Fig. 2 - Un algorithme sur les graphes ET/OU

2 Automates alternants

Un automate alternant est donné par un ensemble fini d'états , un état initial , un ensemble d'états finaux , un alphabet d'entrée , une fonction de transition et une fonction de type . On écrira en abrégé (resp. ) si resp. . On écrira de plus false (resp. true ) lorsque et (resp. ). Dans toute la suite, on supposera que .
désignera le mot vide, la concaténation des mots et la ième lettre du mot (si elle est définie) et la longueur de .
Un calcul de l'automate sur le mot est un arbre étiqueté par et tel que:
  • La racine de l'arbre est étiquetée par . (C'est le noeud de l'arbre de profondeur 0 ).
  • Si un noeud de l'arbre, de profondeur , est étiqueté par et si , et , alors a exactement un fils (de profondeur ) étiqueté par l'un des états . Noter que l'on doit avoir et donc qu'un calcul ne peut pas utiliser de transition false .
  • Si un noeud de l'arbre, de profondeur , est étiqueté par et si , et , alors a exactement fils (de profondeur ), étiquetés respectivement par . Noter que, si (c'est à dire true ), est une feuille.
  • Tous les noeuds de sont de profondeur inférieure ou égale à .
Un calcul de sur est réussi si, toute feuille de de profondeur est étiquetée par un état final. (Noter que, si le calcul ne comprend aucune feuille de profondeur , il est toujours réussi). Le langage accepté par est l'ensemble des mots de tels qu'il existe un calcul réussi de sur .

Question 8

On considère l'automate alternant dont la fonction de transition est donnée par :
0 1
true
false true
false
0 1
L'état initial est . Il n'y a pas d'état final.
Donner des calculs réussis de l'automate sur les mots 0101, 0110, 0111.
La taille d'un automate non-déterministe est égale à la somme de son nombre d'états et de son nombre de transitions. La taille d'un automate alternant est la somme, pour tous les états et pour toutes les lettres de l'alphabet , du cardinal de et du nombre d'états :

Question 9

Montrer que tout langage reconnu par un automate fini non-déterministe est aussi reconnu par un automate alternant de taille

Question 10

Démontrer que, étant donné un automate alternant , on peut calculer en temps un automate alternant qui accepte le complémentaire du langage accepté par . (Ind : on pourra considérer l'automate dual obtenu en échangeant et d'une part et les états finaux et non finaux d'autre part)

Question 11

Donner un algorithme de complexité qui, étant donnés un mot et un automate alternant détermine si est accepté par .

Question 12

Montrer que tout langage reconnu par un automate alternant est aussi reconnu par un automate non-déterministe .
Quelle est la complexité d'un algorithme calculant à partir de ?

Question 13

  1. On considère le langage qui contient le mot unique . Montrer que tout automate non-déterministe acceptant comporte au moins états.
  2. Donner un automate alternant qui accepte , et de taille . (Ind : on pourra considérer les états à partir desquels sont acceptés les mots de la forme où le ième bit dans l'écriture en base 2 de est 0 .).

A Exemple d'un petit langage algorithmique

instructions élémentaires : l'affectation , l'affichage print , les appels de procédures , l'identité skip .
structures de contrôle :
: composition séquentielle des instructions
begin end : parenthèsage (on peut aussi utiliser une indentation)
if then else : conditionnelle
if then : abréviation de if then else skip.
for to do : itération (dont les bornes sont calculées avant entrée dans la boucle;
sont de type entier)
Tant que faire Fin Tq : boucle, le test d'arrêt étant évalué à chaque itération.
ENS Informatique MP PC 2004 - Version Web LaTeX | WikiPrépa | WikiPrépa