Version interactive avec LaTeX compilé
CONCOURS ENSAM - ESTP - ECRIN - ARCHIMEDE
Epreuve de Physique PC durée 4 heures
L'utilisation de la calculatrice est autorisée
Gouttes et flaques : formes et déformations
Lorsqu'un liquide est déposé sur une surface plane horizontale, il forme généralement une goutte ou, si son volume est important, une flaque. La ligne où se coupent les trois interfaces solide/liquide, liquide/vapeur et vapeur/solide est appelée ligne triple: par exemple pour une goutte ayant la symétrie de révolution cette ligne triple est un cercle de rayon
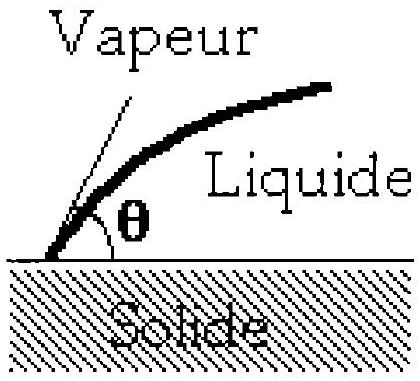
Figure 1
Dans la partie A on étudie une méthode optique de mesure de l'angle de contact. Dans la partie
Tournez la page S.V.P.
à l'équilibre des gouttes sphériques. Le profil d'une flaque sera étudié dans la partie C. Dans la partie
à l'équilibre des gouttes sphériques. Le profil d'une flaque sera étudié dans la partie C. Dans la partie
Aucune connaissance préalable sur les forces de tension superficielle n'est requise: les quelques notions utiles sont introduites au fur et à mesure des besoins. Les différentes parties du problème sont indépendantes.
Partie A: Mesure optique d'un angle de contact
On envisage le dispositif représenté sur la figure 2 : une goutte de liquide ayant la symétrie de révolution autour de l'axe Oz est posée sur le plan solide
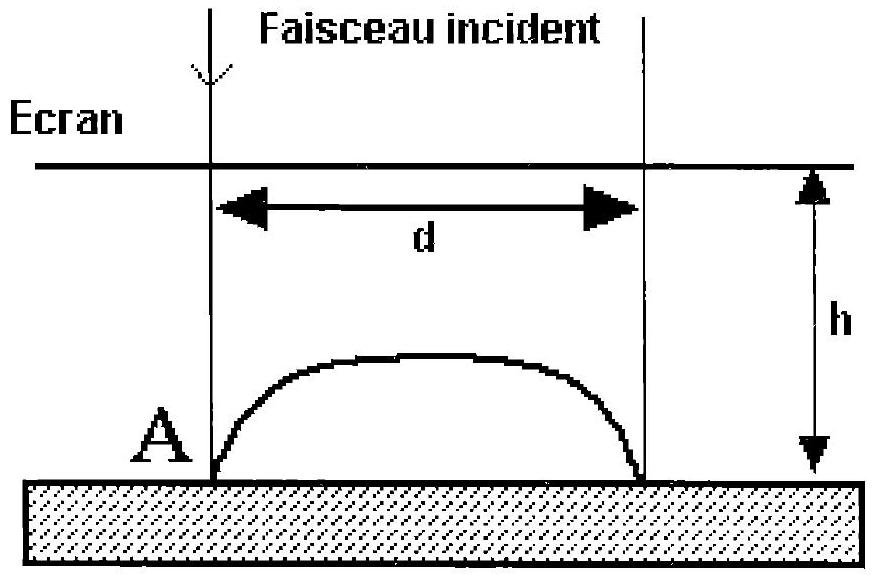
Figure 2
A. I Le faisceau réellement issu du laser possède un diamètre
A.II Soit un rayon incident arrivant sur la goutte en un point
A.III Soit un rayon lumineux frappant la goutte ailleurs que sur la ligne triple ; soit l'angle
A.IV En déduire le diamètre D de la tache observée en fonction de
A.V En donnant l'ordre de grandeur de l'angle sous lequel le faisceau est diffracté par la goutte de diamètre
A.II Soit un rayon incident arrivant sur la goutte en un point
A.III Soit un rayon lumineux frappant la goutte ailleurs que sur la ligne triple ; soit l'angle
A.IV En déduire le diamètre D de la tache observée en fonction de
A.V En donnant l'ordre de grandeur de l'angle sous lequel le faisceau est diffracté par la goutte de diamètre
Partie B : Une goutte posée sur un solide peut elle être sphérique ?
B.I On envisage une goutte de liquide
normes respectives
normes respectives
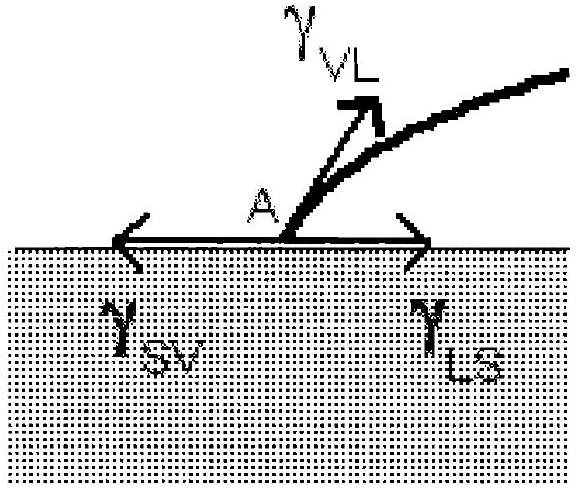
Figure 3
B.I. 1 On envisage une évolution de la ligne triple au cours duquel son rayon passerait spontanément de la valeur
B.I. 2 En déduire que le travail total sur toute la ligne triple vaut :
B.I. 2 En déduire que le travail total sur toute la ligne triple vaut :
où
B.I.3. A l'équilibre, le système n'évolue plus spontanément; on admettra que cette situation correspond à
B.I.3. A l'équilibre, le système n'évolue plus spontanément; on admettra que cette situation correspond à
B.I. 4 : Lorsque
B.II.1: Considérons maintenant une surface plane hétérogène constituée par deux types de surfaces caractérisées respectivement par les angles de contact
B.II.1: Considérons maintenant une surface plane hétérogène constituée par deux types de surfaces caractérisées respectivement par les angles de contact
B.II. 2 : On constate expérimentalement que sur une surface hydrophobe (
B.II. 3 : En appliquant la relation de Cassie-Baxter, en déduire le cosinus de l'angle de contact apparent
B.II.4: Pour que la goutte soit sphérique, quelle doit être la valeur de l'angle de contact apparent
B.II. 5 : Quelle valeur de
B.II. 3 : En appliquant la relation de Cassie-Baxter, en déduire le cosinus de l'angle de contact apparent
B.II.4: Pour que la goutte soit sphérique, quelle doit être la valeur de l'angle de contact apparent
B.II. 5 : Quelle valeur de
Partie C : Forme d'une flaque
Lorsque les dimensions d'une goutte déposée sur une surface sont suffisamment grandes, les effets gravitationnels l'aplatissent, on parle alors de «flaque». On cherche ici la forme d'une flaque sur un plan solide horizontal d'équation
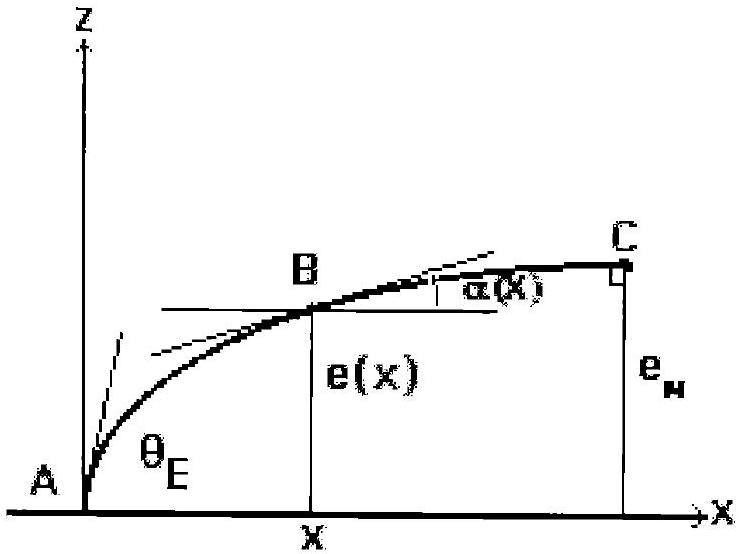
Figure 4
C.I. 1 : L'eau, de masse volumique
C.I. 2 : En considérant un élément dS de l'interface Liquide/Vapeur au voisinage de B (correspondant à la partie du liquide comprise entre les cotes
abscisses x et
C.I. 3 : En déduire l'expression de la composante selon Ox de la somme des forces de pression subies par la partie de l'interface comprise entre
C.II L'interface
C.III. 1 : En considérant que l'interface est à l'équilibre, montrer que le profil
C.I. 2 : En considérant un élément dS de l'interface Liquide/Vapeur au voisinage de B (correspondant à la partie du liquide comprise entre les cotes
abscisses x et
C.I. 3 : En déduire l'expression de la composante selon Ox de la somme des forces de pression subies par la partie de l'interface comprise entre
C.II L'interface
C.III. 1 : En considérant que l'interface est à l'équilibre, montrer que le profil
où
C.III. 2 : En déduire l'expression de
C.IV On suppose
C.III. 2 : En déduire l'expression de
C.IV On suppose
Déterminer l'expression de
C.V A quelle condition sur le rapport
C.V A quelle condition sur le rapport
Partie D : Déformations de la ligne de contact
Lorsque la ligne triple est perturbée par un défaut, se comporte-t-elle comme une corde élastique? Cette partie est consacrée à l'étude de cette question dans le cas d'une flaque (
Lorsque la perturbation due à un défaut de la surface, situé à l'origine des espaces, est localisée sur une distance très petite devant toutes les autres dimensions du problème, l'interface liquide-vapeur au voisinage de la ligne triple, qui à l'équilibre apparaîtrait comme une portion du plan vertical
D.I : Rappeler les deux équations locales de Maxwell de l'électrostatique. En déduire l'équation aux dérivées partielles (équation de Poisson) dont est solution le potentiel électrique
D.II: Ecrire l'équation de Poisson que devrait vérifier le potentiel électrostatique créé par un fil cylindrique, d'axe
D.III En utilisant le théorème de Gauss, établir l'expression du champ électrostatique en fonction de la distance
admettra que la solution électrostatique obtenue pour tout l'espace est applicable au problème de la flaque dans le demi-espace
D.IV: En déduire la forme
D.V : Comparer cette forme avec celle qui serait prise par un élastique fixé par ses extrémités et pincé en son milieu. La ligne triple se comporte-t-elle comme une corde élastique?
D.I : Rappeler les deux équations locales de Maxwell de l'électrostatique. En déduire l'équation aux dérivées partielles (équation de Poisson) dont est solution le potentiel électrique
D.II: Ecrire l'équation de Poisson que devrait vérifier le potentiel électrostatique créé par un fil cylindrique, d'axe
D.III En utilisant le théorème de Gauss, établir l'expression du champ électrostatique en fonction de la distance
admettra que la solution électrostatique obtenue pour tout l'espace est applicable au problème de la flaque dans le demi-espace
D.IV: En déduire la forme
D.V : Comparer cette forme avec celle qui serait prise par un élastique fixé par ses extrémités et pincé en son milieu. La ligne triple se comporte-t-elle comme une corde élastique?
Partie E: Dynamique de l'étalement d'une goutte
Lorsqu'on dépose une petite goutte sur une surface propre, on constate expérimentalement que si
Figure 5
E.I On rappelle que pour prendre en compte la viscosité
E.II On envisage dans cette seule question un écoulement modèle: un liquide visqueux de masse volumique
E.II. 1 Montrer que l'accélération des particules de fluide est nulle.
E.II. 2 Montrer que
E.II. 3 En déduire que la plaque (1) (respectivement (2)) exerce une force surfacique de viscosité
E.II. 4 On envisage le système fermé ( S ) constitué du liquide contenu à l'instant t entre deux éléments de surface dS se faisant face sur les deux plaques, centrés en deux points
E.II. 5 En appliquant le théorème de l'énergie cinétique à (
E.III. On revient désormais à l'étude de l'écoulement dans la goutte qui s'étale. On admet que l'expression de la puissance des forces intérieures de viscosité dans un élément de volume
E.III. 1 Exprimer la puissance totale des forces intérieures de viscosité pour toute la goutte en fonction de
E.III. 2 En utilisant la puissance des forces de tension superficielle donnée dans le préambule de cette partie et en négligeant tout autre terme dans le bilan énergétique (notamment toute variation d'énergie cinétique), en déduire une équation différentielle reliant
E.III. 3 Le volume constant
E.II On envisage dans cette seule question un écoulement modèle: un liquide visqueux de masse volumique
E.II. 1 Montrer que l'accélération des particules de fluide est nulle.
E.II. 2 Montrer que
E.II. 3 En déduire que la plaque (1) (respectivement (2)) exerce une force surfacique de viscosité
E.II. 4 On envisage le système fermé ( S ) constitué du liquide contenu à l'instant t entre deux éléments de surface dS se faisant face sur les deux plaques, centrés en deux points
E.II. 5 En appliquant le théorème de l'énergie cinétique à (
E.III. On revient désormais à l'étude de l'écoulement dans la goutte qui s'étale. On admet que l'expression de la puissance des forces intérieures de viscosité dans un élément de volume
E.III. 1 Exprimer la puissance totale des forces intérieures de viscosité pour toute la goutte en fonction de
E.III. 2 En utilisant la puissance des forces de tension superficielle donnée dans le préambule de cette partie et en négligeant tout autre terme dans le bilan énergétique (notamment toute variation d'énergie cinétique), en déduire une équation différentielle reliant
E.III. 3 Le volume constant
