Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.

L'usage de calculatrices est interdit.

AVERTISSEMENT

L'épreuve est composée de 5 exercices, totalement indépendants. Le langage à utiliser pour un exercice est indiqué à côté du numéro de l'exercice.

Un candidat pourra toujours admettre le résultat des questions qu'il n'a pas faites pour faire les questions suivantes.

La présentation, la lisibilité, l'orthographe, la qualité de la rédaction, la clarté et la précision des raisonnements entreront pour une part importante dans l'appréciation des copies. En particulier, les résultats non justifiés ne seront pas pris en compte. Les candidats sont invités à encadrer les résultats de leurs calculs.

Exercice 1 (Python)

On dit qu'une fonction termine si elle renvoie une valeur ou si elle lève une exception (par exemple ZeroDivisionError). Une fonction peut terminer ou continuer à calculer à l'infini. Ainsi, la fonction fun1 (voir ci-dessous), pour un entier n , termine pour n inférieur ou égal à 10 (elle renvoie None) et ne termine pas pour

strictement plus grand que 10. En outre, cette fonction termine pour une chaîne de caractères n (en levant l'exception TypeError).

Pour quelles valeurs de n dans la fonction fun2 termine-t-elle? Même question pour fun3.

def fun1 (n): def fun2 (n): def fun3 (n):
    while n != 10: if n % 2 == 0: S = 0
        n = n + 1 return 0 while n != 0 :
            else : S = S + n
                while True: n = n - 2
                    n = n + 1 return S

Détailler l'exécution de fun3(10).
Écrire en Python une fonction ForEver (n) qui ne termine jamais.

Le module dis permet, à partir du nom d'une fonction, de trouver quel est le bytecode Python qu'elle exécute, et d'analyser ce bytecode. On se demande quelles propriétés sur la fonction peuvent être déduites de cette analyse. Plus précisément, nous souhaitons répondre au problème suivant.

Problématique

Est-il possible d'écrire en Python une fonction arret, qui termine toujours, et telle que arret (

) renvoie True si le calcul de

termine et False sinon?
4. Dans cette question, nous supposons qu'une telle fonction arret existe.
(a) Écrire en Python une fonction strange (

) qui termine si et seulement si le calcul de

ne termine pas.
(b) Écrire en Python une fonction paradox (f) qui termine si et seulement si le calcul de

ne termine pas.
5. Le calcul de paradox(paradox) termine-t-il ? Qu'en déduire quant à l'existence de arret?

Exercice 2 (Caml)

Tout entier naturel non nul

s'écrit de manière unique

avec

un entier naturel (qui peut valoir zéro) et

un entier naturel impair. Dans la suite de cet exercice, nous appelons valuation de

l'entier

et résidu de

l'entier

. Par convention, le résidu de zéro est zéro.

Expliquer succintement comment, à partir de l'écriture en base deux de , on peut lire la valuation et le résidu de .
L'entier 192 s'écrit en base deux 11000000 . Donner sa valuation et son résidu.
Écrire en Caml une fonction residu : int -> int qui prend en argument un entier positif ou nul et renvoie son résidu.

Pour calculer le pgcd (plus grand commun diviseur) de deux entiers, nous pouvons utiliser l'algorithme des soustractions successives décrit ci-après.

1 Entrées : deux entiers naturels non nuls

2 Tant que

est non nul :
3 Remplacer

par

.
4 Remplacer

par le minimum de

et de l'ancienne valeur de

.
5 Fin du "Tant que".
6 Renvoyer

4. Écrire en Caml une fonction pgcd1 : int -> int -> int qui calcule le pgcd de deux entiers naturels non nuls en utilisant cet algorithme et pas un autre. Cette fonction ne doit pas être récursive ni faire appel à une ou des fonctions auxiliaires récursives.
5. Écrire en Caml une fonction récursive pgcd2 : int

int

int qui calcule le pgcd de deux entiers naturels non nuls en utilisant la méthode des soustractions successives.
6. Estimer (en justifiant) la complexité de cet algorithme en fonction de

La méthode chinoise, mentionnée dans Les Neuf Chapitres sur l'art mathématique écrit aux débuts de la dynastie Han, consiste à remplacer la ligne 3 par la ligne suivante :

Remplacer

par le résidu de

On admet que cette méthode permet de calculer le pgcd de

est impair. Ce résultat peut notamment être utilisé pour répondre à la question suivante.
7. Que calcule la méthode chinoise lorsque

sont pairs ? Le démontrer laconiquement.
Indication : On peut distinguer le cas

du cas

.
8. Estimer (en justifiant) la complexité de cette méthode en fonction de

, dans le cas où

sont tous les deux impairs.
9. En déduire une fonction pgcd_chinois : int -> int -> int qui calcule le pgcd de deux entiers (pairs ou impairs) avec une complexité du même ordre de grandeur que la complexité calculée la question précédente. Justifier la complexité de pgcd_chinois.

Exercice 3 (Caml)

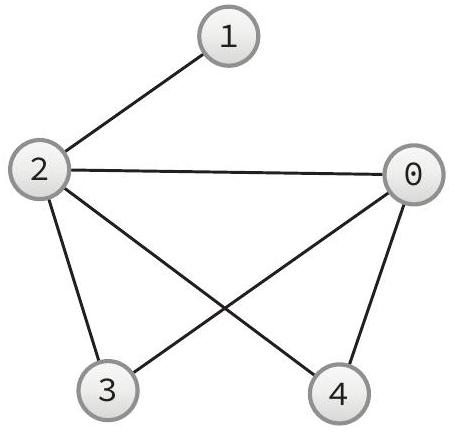
Écrire la matrice d'adjacence du graphe ci-dessus.
Écrire en Caml une fonction chemin : int vect vect -> int list -> bool qui prend en entrée la matrice d'adjacence d'un graphe et un chemin (une liste de sommets du graphe) et qui vérifie si ce chemin est possible dans le graphe. Par exemple, sur le graphe ci-dessus, avec le chemin [ ] la fonction chemin doit renvoyer false car les sommets 1 et 0 ne sont pas connectés. Avec le chemin [ ] la fonction chemin doit renvoyer true car les sommets 1 et 2 sont connectés, ainsi que les sommets 2 et 3.

Exercice 4 (SQL)

Nous nous intéressons à une base de données des zoos qui contient deux tables. La première table, zoos, a quatre colonnes dont id, un identifiant unique pour chaque zoo. Quelques lignes sont données ci-après.

id	nom	pays	continent
FR42	Zoo de La Flèche	France	Europe
RU12	Parc zoologique de Novossibirsk	Russie	Asie
RU5	Parc zoologique de Saint-Pétersbourg	Russie	Europe

La seconde table, animaux, a 6 colonnes, notamment un identifiant unique pour chaque animal (id) et l'identifiant du zoo qui héberge l'animal (zoo).

id	nom	espece	sexe	naissance	zoo
ke860	Kaiko	Chameau	F	2013	FR42
ic431	Jeffrey	Python royal	M	2016	RU12
gz599	Antaeus	Annaconda vert	M	2016	RU12

Les questions suivantes demandent d'écrire des requêtes SQL. À chaque fois quelques lignes de la table attendue sont données en exemple.

Écrire une requête SQL renvoyant la table des chamelles (chameaux femelles).

id	nom	naissance	zoo
ke860	Kaiko	2013	FR42
md375	Aimy	2012	CG01

Écrire une requête renvoyant la table des bonobos mâles vivant en Asie.

id	nom	naissance	zoo
yv919	Finn	2008	CN33
qv139	Proteus	2013	KR08

Écrire une requête renvoyant la liste des pays ayant des zoos sur plusieurs continents.

pays

Russie

Exercice 5 (Caml)

Une formule positive est une formule propositionnelle n'utilisant comme connecteurs logiques que "ou" et "et". Ces connecteurs sont notés, respectivement,

. On représente les formules positives en Caml par le type suivant :
type

of string ;;

Considérons la formule " " et notons-la .
(a) Dessiner l'arbre correspondant à .
(b) Écrire en Caml en utilisant le type fp.

On définit par récurrence les disjonctions de variables propositionnelles (DVP) ainsi :

Si est une variable propositionnelle, alors est une DVP.
Si et sont des DVP alors est aussi une DVP.

Écrire en Caml une fonction dvp : fp -> bool prenant en argument une formule positive et renvoyant true si et seulement si est une DVP.

On appelle forme normale conjonctive positive (FNCP) une conjonction de DVP. Ainsi

est une forme normale conjonctive positive, mais pas

. Plus précisément, on définit les FNCP par récurrence comme suit :

Si est une DVP alors est une FNCP.
Si et sont des FNCP, alors aussi.

Écrire en Caml une fonction fncp de type fp -> bool prenant en argument une formule positive et renvoyant true si et seulement si est une FNCP.

On définit la fonction norm qui, étant donné une formule positive

, renvoie une FNCP logiquement équivalente à

let rec norm f = match f with 0
    VAR _ -> f
    1
    | OU ET (norm a, norm b) -> E)
    | | | | | | | | | | (a,c) ) ) , norm (OU }
    | OU (a,b) -> let c = OU( norm a, norm b) in 5
        if f=c

        else norm c;; 8

Expliquer brièvement pourquoi si est une FNCP alors norm termine et renvoie f.
Montrer que si norm termine, alors elle renvoie une FNCP.
Exhiber, sans démonstration, une fonction simple de l'ensemble des formules dans telle que pour toutes formules et :

,
,
Si et alors .

On introduit la fonction

de l'ensemble des formules dans

est la profondeur minimale d'un nœud ET dans la formule

. Plus précisément,

est définie comme suit :

si est une variable propositionnelle,
pour toutes formules et ,
pour toutes formules et .

On considère une formule telle que :

correspond au cas de filtrage (pattern matching en anglais) de la ligne 5 mais ne correspond à aucun des cas des lignes 1 à 4,
Le calcul de à la ligne 5 termine.
(a) Montrer que si alors .
(b) Montrer que .

Démontrer soigneusement que norm termine sur toutes les formules positives.