CONCOURS ARTS ET MÉTIERS ParisTech - ESTP - ARCHIMEDE

Épreuve d'Informatique MP

Durée 3 h

L'usage de calculatrices est interdit.

Exercice 1

verification_liste
    données L:liste d'entiers naturels
    résultat b:booléen

tri_tableau
    données N: entier naturel
        T:tableau d'entiers naturels de longueur N
    résultat U:tableau d'entiers naturels de longueur N

Exercice 2

Exercice 3

1. On considère le programme suivant qui prend en entrée une liste contenant des listes de longueur fixée ne contenant que des 0 ou des 1 et retourne une liste de même type. On remarquera qu'une liste de listes peut contenir uniquement la liste vide.

$\operatorname{PROG}(L$ : liste de listes, $k$ : entier naturel non nul )
variables : $x$ : entier, $U$ : liste de listes, $V 0$ : liste de listes, $V 1$ : liste de listes.
$W 0$ : liste de listes, $W 1$ : liste de listes, $L 1$ : liste d'entiers,
$U \leftarrow L$
$V 0 \leftarrow$ liste_vide
$V 1 \leftarrow$ liste_vide
$W 0 \leftarrow$ liste_vide
$W 1 \leftarrow$ liste_vide
tant que test_liste_vide $(U)=0$ faire
        $L 1 \leftarrow$ tête $(U)$
        $x \leftarrow$ tête $(L 1)$
        si ( $x=0$ ) alors ajouter(supprimer_tête( $L 1$ ), $V 0$ )
        sinon ajouter(supprimer_tête(L1), V1)
        fin si
        supprimer_tête $(U)$
        fin faire
si $(k>1)$ faire $V 1 \leftarrow P R O G(V 1, k-1)$
    $V 0 \leftarrow P R O G(V 0, k-1)$
fin si
tant que test_liste_vide $(V 1)=0$ faire
        $L 1 \leftarrow$ tête $(V 1)$
        ajouter $(1, L 1)$
        ajouter( $L 1, W 1$ )
        supprimer_tête(V1)
        fin faire
tant que test_liste_vide $(V 0)=0$ faire
        $L 1 \leftarrow$ tête $(V 0)$
        ajouter $(0, L 1)$
        ajouter( $L 1, W 0$ )
        supprimer_tête( $V 0$ )
        fin faire
tant que test_liste_vide $(W 0)=0$ faire
        ajouter(tête( $W 0$ ), $U$ )
        supprimer_tête( $W 0$ )
        fin faire
tant que test_liste_vide $(W 1)=0$ faire
        ajouter(tête( $W 1$ ), $U$ )
        supprimer_tête( $W 1$ )
        fin faire
retourner $(U)$

FONCTION1( $n$ : entier naturel, $k$ : entier naturel)
variables : $x$ : entier, $y$ : entier, $i$ : entier, $L$ : liste d'entiers.
$L \leftarrow$ liste_vide
$x \leftarrow n$
pour $i$ de 1 à $k$ faire
    $y \leftarrow x$ MOD 2
    ajouter $(y, L)$
    $x \leftarrow(x-y) / 2$
    fin faire
retourner $L$

3. Qu'effectue la fonction ci-dessous :

FONCTION2( $L:$ liste d'entiers naturels, $k:$ entier nature)
variables : $x$ : entier, $y$ : entier, $i$ : entier, $L 1$ : liste d'entiers, $L 2$ : liste d'entiers, $U$ : liste de listes.
$L 1 \leftarrow L$
$U \leftarrow$ liste_vide
tant que test_liste_vide $(L 1)=0$ faire
    $x \leftarrow$ tête $(L 1)$
    $L 2 \leftarrow \operatorname{FONCTION1}(x, k)$
    ajouter $(L 2, U)$
    supprimer_tête(L1)
    fin faire
retourner $U$

4. a) Décrire l'éxécution de la fonction FONCTION2 sur la liste et l'entier ? Quel est le résultat de ?
   b) On souhaite utiliser la fonction FONCTION1, la FONCTION2 et le programme PROG pour trier par ordre croissant des listes d'entiers naturels. Quelle(s) fonction(s) faut-il ajouter? Quel est le domaine de validité de ce programme de tri ?

Exercice 4

1. Dans cette question, est l'alphabet à deux lettres . Déterminer l'ensemble des sous-mots du mot xyxyx. Combien y-en a t'il?
2. Dans le cas général, démontrer que l'ensemble des sous-mots du mot est fini et proposer une majoration de son cardinal en fonction de .
3. On suppose que est un sous-mot de . Soit l'ensemble des applications application strictement croissante de dans telle que , pour tout entier compris entre 1 et .
   a) Soit le plus petit indice dans tel que . Démontrer que toute application dans vérifie .
   b) Démontrer qu'il existe une application dans telle que, pour toute application dans et tout indice dans .
   c) Ecrire un algorithme qui prend en entrée les listes et et qui renvoie la liste .
   d) Ecrire un algorithme qui prend en entrée les listes et et qui renvoie un booléen égal à 1 si est un sous-mot de sinon. L'algorithme ne doit parcourir qu'une fois chacune des listes et . Estimer la complexité de votre algorithme en fonction des entiers et .
4. Le cardinal de l'ensemble est noté . Soient et les mots tels que et .
   a) Lorsque , démontrer l'égalité .
   b) Lorsque , démontrer l'égalité .
   c) Proposer un algorithme récursif qui prend en entrée les listes et et qui renvoie la valeur de .
5. Dans cette partie, le mot est fixé. On considère le langage formé par les mots de tels que est un sous-mot de .
   a) Dans le cas particulier où est l'alphabet à deux lettres et , on remarquera que le langage est le langage reconnu par l'automate représenté dans la figure 1 ci-dessous. Proposer une expression rationnelle de .
   b) Dans le cas général, démontrer que le langage est un langage rationnel et en proposer une expression rationnelle.
   c) Représenter graphiquement un automate déterministe qui reconnait le langage . On démontrera précisément que le langage reconnu est .

Figure 1: Automate

Exercice 5

1. Ecrire la table de vérité de la fonction .
2. Démontrer la propriété d'associativité de la fonction , c'est-à-dire :

3. Ecrire avec une formule booléenne.
4. Construire un circuit logique implémentant la fonction utilisant uniquement des portes XOR (ou exclusif).
5. Etant donné un entier naturel non nul, construire un circuit logique qui prend en entrée bits et donne en sortie la parité du nombre de ces bits égaux à 1 en utilisant au plus portes XOR.

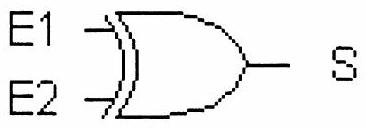
Figure 2: Porte XOR (ou exclusif)