Version interactive avec LaTeX compilé

E3A Option Informatique MP 2006

Notez ce sujet en cliquant sur l'étoile

0.0(0 votes)

🔗 Explorer

E3A MP E3A 2006 MP Info Info 2006

2025_08_29_2ce0088c4881c3d9e5c8g

CONCOURS ENSAM - ESTP - EUCLIDE - ARCHIMEDE

Epreuve d'Informatique MP
durée 3 heures

Si, au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, d'une part il le signale au chef de salle, d'autre part il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.

L'usage de la calculatrice est interdit

Indiquer en tête de copie ou de chaque exercice le langage utilisé.
On utilisera la notation pour accéder à l'élément d'un tableau .
On indicera les tableaux à partir de 1, quitte à ne jamais prendre en compte l'élément d'indice 0 dans un langage où les tableaux sont indicés à partir de 0 .

1. Le tri par sélection

Le tri (croissant) par sélection d'un tableau

éléments consiste à rechercher le plus grand élément, le permuter avec l'élément situé en fin de tableau, et à itérer le traitement avec un élément de moins, jusqu'à ce qu'il n'y ait plus qu'un seul élément.

1.1. Écrire la fonction

indiceMaxi données t : tableau d'entiers,
    n : entier;
    résultat : entier;

qui recherche dans un tableau

entiers le plus grand entier et retourne son
indice. S'il y a plusieurs maxima égaux, elle retourne l'indice du premier de ceux-ci.

1.2. Écrire la fonction ITÉRATIVE

triSelec1 donnée-résultat t : tableau d'entiers ;
    donnée n : entier;
    résultat : sans retour
qui trie par sélection le tableau t de n entiers.

1.3. Écrire la fonction RÉCURSIVE

triSelec2 donnée-résultat t : tableau d'entiers ;
    donnée n: entier;
    résultat : sans retour
qui trie par sélection le tableau t de n entiers.

1.4. Donner la complexité de ce tri.

2. Tri par insertion

Le tri (croissant) par insertion d'un tableau

éléments consiste à rechercher itérativement la place d'insertion de l'élément

dans le sous-tableau précédent (indicé de 1 à

) supposé trié et à l'insérer à sa place. On commence à partir du deuxième élément et on termine quand tous les éléments ont été placés.

La recherche de la place d'insertion peut se faire séquentiellement ou par dichotomie.
2.1. Expliquer brièvement les deux principes de recherche (séquentielle et dichotomique) et donner leurs complexités (en moyenne et au pire).

2.2. Écrire la fonction

    posInser1 données t : tableau d'entiers,
        n: entier,
        x : entier;
        résultat : entier;
    qui recherche séquentiellement dans un tableau t trié de n entiers la place
d'insertion de x.

2.3. Écrire la fonction

    posInser2 données t : tableau d'entiers,
        n: entier,
        x : entier;
        résultat : entier;
    qui recherche par dichotomie dans un tableaut trié de n entiers la place d'insertion
de x.

2.4. Écrire la fonction

    decale donnée-résultat t : tableau d'entiers ;
        données i : entier,
            j : entier;
        résultat : sans retour
    qui décale d'une position vers la droite tous les éléments du tableau t depuis
l'indice i jusqu'à l'indice j (compris)

2.5. Écrire la fonction ITÉRATIVE

triInser donnée-résultat t : tableau d'entiers ;
    donnée n: entier ;
    résultat : sans retour
qui trie par insertion le tableau t de n entiers.

3. Tri rapide (quick sort)

Le principe du quick sort est de partitionner le tableau à trier (s'il a au moins deux éléments) en trois sous-tableaux, le premier comprenant tous les éléments inférieurs ou égaux à un élément (l'élément pivot), le deuxième ne contenant qu'un seul élément ('élément pivot) et le troisième contenant tous les éléments supérieurs ou égaux à l'élément pivot. Puis on réapplique récursivement le quick sort sur les premier et troisième sous-tableaux (l'élément pivot, lui, est à sa place définitive).

Soit les fonctions
partition donnée-résultat

: tableau d'entiers ;
données

: entier,

: entier;
résultat : entier
qui opère sur le sous-tableau

compris entre les indices

, prend

comme élément pivot, déplace les éléments inférieurs ou égaux au pivot en début de soustableau, les éléments supérieurs ou égaux au pivot en fin de sous-tableau, positionne le pivot à sa place définitive et retoume la valeur de cette place
et
quicksort donnée-résultat

: tableau d'entiers ;
données

: entier,

: entier;
résultat: sans retour
qui trie le tableau

entre les indices

(compris)
Soit le tableau suivant :

	5	1	12	3	24	8	10	2	14	7	2	9	4	17
indice	1	2	3	4	5	6	7	8	9	10	11	12	13	14

3.1. Donner un contenu possible de t après l'appel à partition(

), et la valeur de retour de la fonction
3.2. Avec quels paramètres doit-on appeler quicksort pour continuer le tri après cette partition ?

3.3. Écrire la fonction quicksort

3.4. Écrire la fonction partition

On pourra utiliser deux parcours, l'un allant du début du sous-tableau vers la fin, et l'autre allant de la fin vers le début. Le parcours montant sera suspendu quand un élément sera supérieur au pivot ; le parcours descendant sera suspendu quand un élément sera inférieur au pivot. Les éléments seront alors échangés et les parcours reprendront jusqu'à ce qu'ils se rejoignent. La place du pivot sera alors déterminée, le pivot y sera mis, et sa place retournée.

4. Le tri par tas (heap sort)

Le tri par tas consiste à interpréter le tableau comme un arbre binaire presque parfait, à le transformer en tas, puis itérativement, à permuter la racine de l'arbre avec la dernière feuille, puis, à reconstituer le tas avec un élément de moins et ce jusqu'à ce qu'il n'y ait plus qu'un élément à traiter.

Définitions

Arbre :Un arbre est soit un arbre atomique (une feuille), soit un nœud (père) et une suite de sous-arbres (ses fils). Chaque nœud ou feuille de l'arbre est associé à une valeur. Graphiquement, on peut représenter un arbre comme suit:

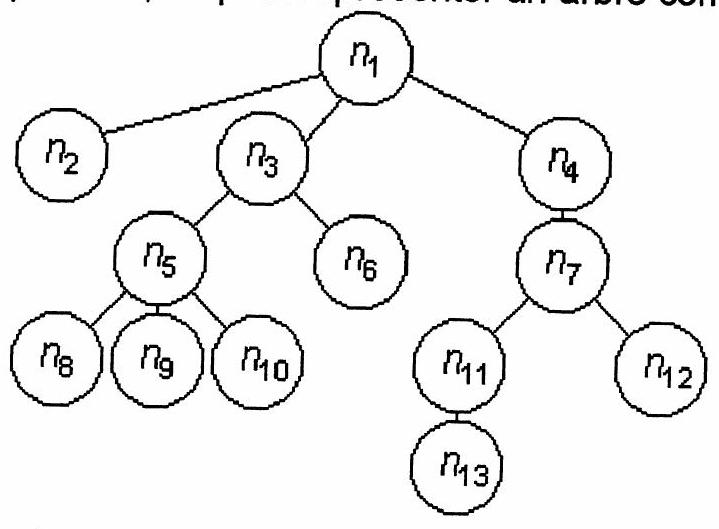
Ici, par exemple, le nœud

a pour fils

et pour père

est appelé la racine de l'arbre et les feuilles en sont

Arbre binaire : arbre où chaque nœud est associé au maximum à deux sousarbres
Arbre binaire presque complet (ABPC) : arbre binaire dans lequel tous les niveaux de profondeur, sauf peut-être le dernier contiennent le maximum de nœuds, et les feuilles du dernier niveau sont toutes à gauche. Exemple d'arbre binaire presque complet

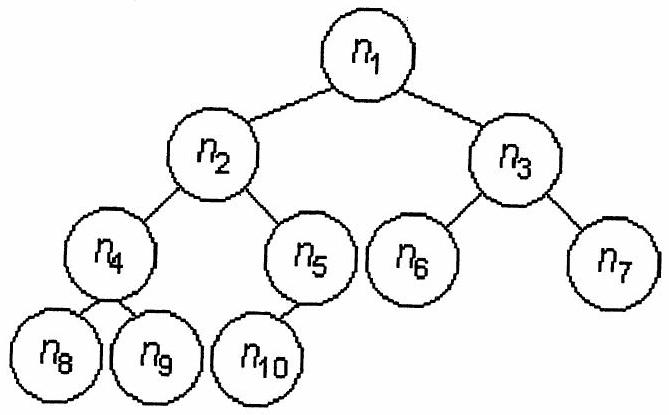
Un ABPC peut être représenté par un tableau (représentation tabulaire) et réciproquement, un tableau peut être interprété comme un arbre binaire presque complet.

Ici, le tableau

indice


1	2	3	4	5	6	7	8	9	10

peut être interprété comme l'ABPC de la figure.

Tas: Un tas est ABPC dans lequel chaque nœud est dominant (valeur supérieure ou égale à celles de son ou ses fils).

4.1. Dessiner l'arbre représenté par le tableau suivant:

	9	5	8	9	7	6	7	3	6	4
indice	1	2	3	4	5	6	7	8	9	10

4.2. Écrire la fonction

indiceFilsG	donnée	entier,
	résultat	: entier

retourne l'indice du fils gauche (supposé existant) d'un nœud d'indice

dans la représentation tabulaire d'un ABPC

4.3. Écrire la fonction

indiceFilsD donnée i : entier,
    résultat : entier

retourne l'indice du fils droit (supposé existant) d'un nœud d'indice

dans la
représentation tabulaire d'un ABPC

4.4. Écrire la fonction

indicePere donnée i : entier,
    résultat : entier

retourne l'indice du père (supposé existant) d'un nœud d'indice

dans la
représentation tabulaire d'un ABPC

4.5. Écrire la fonction

estFeuille données i : entier,
    n : entier;
    résultat : booléen

qui retourne Vrai si

est l'indice d'une feuille (nœud sans fils) dans la représentation
tabulaire d'un ABPC de taille

, et Faux sinon.

4.6. Écrire la fonction

estPere1 données i : entier,
    n : entier;
    résultat : booléen

qui retourne Vrai si

est l'indice d'un nœud n'ayant qu'un seul fils dans la représentation tabulaire d'un

de taille

, et Faux sinon.

4.7. Écrire la fonction

estPere2 données i : entier,
    n : entier;
    résultat : booléen

qui retourne Vrai si

est l'indice d'un nœud ayant deux fils dans la représentation tabulaire d'un ABPC de taille

, et Faux sinon.

4.8. Écrire la fonction

estDominant données t : tableau d'entiers;
    i : entier,
    n : entier;
        : booléen

qui retourne Vrai si

est l'indice d'une feuille ou d'un nœud dominant (nœud de valeur supérieure ou égale à celles de son ou ses fils) dans la représentation tabulaire

d'un ABPC de taille

, et Faux sinon.

4.9. Écrire la fonction

retablirTas donnée-résultat t : tableau d'entiers;
    données i : entier,
        n : entier;
    résultat : sans résultat

qui opère sur le sous-arbre de

(représentation tabulaire d'un ABPC) à partir de l'indice

pour en faire un tas, avec comme hypothèse que les fils de

(s'ils existent) sont des tas.

Par exemple:

	9	5	8	9	7	6	7	3	6	4
indice	1	2	3	4	5	6	7	8	9	10

retablirTas(

) transformera l'arbre en

	9	9	8	6	7	6	7	3	5	4
indice	1	2	3	4	5	6	7	8	9	10

4.10. Écrire la fonction

construireTas donnée-résultat

: tableau d'entiers;
donnée

: entier;
résultat: sans résultat
qui opère sur

(représentation tabulaire d'un

) pour en faire un tas.
Par exemple:

	1	2	3	4	5	6	7	8	9	10
indice	1	2	3	4	5	6	7	8	9	10

construireTas(

) transformera l'arbre en

	10	9	7	8	5	6	3	1	4	2
indice	1	2	3	4	5	6	7	8	9	10

4.11. Écrire la fonction

heapSort	donnée-résultat	t
donnée	n	tableau d'entiers;
	résultat
		sans résultat

qui trie par tas le tableau

entiers.