Si , au cours de l'épreuve, un candidat repère ce qui lui semble être une erreur d'énoncé, il le signale sur sa copie et poursuit sa composition en indiquant les raisons des initiatives qu'il est amené à prendre.

Indiquer en tête de copie ou de chaque exercice le langage utilisé.

Exercice 1
a) Ecrire la procédure

indicesMax donnée T:tableau d'entiers
    l:entier
    résultat m:entier
    n: entier

qui retourne le plus petit et le plus grand des indices correspondant à la valeur maximale d'un tableau de longueur

.
b) Ecrire la fonction

moyenneNotesMinorées données $L$ :liste d'entiers
        $a$ : entier
    résultat $x$ : réel

qui retourne la moyenne des notes supérieures ou égales à l'entier a dans une liste de notes. Cette liste contient des notes, qui sont des nombres compris entre 0 et 20 , et se termine par la valeur -1 . Dans le cas où cette liste ne comporte aucune note supérieure ou égale à l'entier

, la fonction moyenneNotesMinorées retournera la valeur -1 et affichera un message d'avertissement.

Exercice 2

a) Que calcule le programme suivant :

$u \leftarrow 0$
$v \leftarrow 50$
tant que $v>0$ faire
    $u \leftarrow u+v^{2}$
    $v \leftarrow v-1$
fin tant que
afficher(u)

b) Que calculent les fonctions suivantes :

    A( $n$ : entier )
            si $(n \geq 0) \quad$ faire $\mathrm{A}(n) \leftarrow n$
            sinon faire $\mathrm{A}(n) \leftarrow-n$
P ( $n$ : entier)
    $n \leftarrow \mathrm{~A}(n)$
    si $(n=0) \quad$ faire $\mathrm{P}(n) \leftarrow 0$
    sinon, $\quad$ si $(n=1) \quad$ faire $\mathrm{P}(n) \leftarrow 1$
        sinon $\quad$ faire $\mathrm{P}(n) \leftarrow \mathrm{P}(n-2)$
$\mathrm{S}(m:$ entier $, n:$ entier $)$
        si $(\mathrm{A}(m) \leq \mathrm{A}(n)) \quad$ faire $\mathrm{S}(m, n) \leftarrow \mathrm{A}(m)$
        sinon $\quad$ faire $\mathrm{S}(m, n) \leftarrow \mathrm{A}(n)$

    D( $m:$ entier $, n:$ entier )
si $(m=0) \quad$ faire $\mathrm{D}(m, n) \leftarrow \mathrm{A}(n)$
si $(n=0) \quad$ faire $\mathrm{D}(m, n) \leftarrow \mathrm{A}(m)$
si $(m \neq 0)$ et si $(n \neq 0)$ faire
si $(\mathrm{P}(m)=0)$ et $(\mathrm{P}(n)=0)$ faire $\mathrm{D}(m, n) \leftarrow 2 * \mathrm{D}(m / 2, n / 2)$
si $(\mathrm{P}(m)=0)$ et $(\mathrm{P}(n)=1) \quad$ faire $\mathrm{D}(m, n) \leftarrow \mathrm{D}(m / 2, n)$
si $(\mathrm{P}(m)=1)$ et $(\mathrm{P}(n)=0)$ faire $\mathrm{D}(m, n) \leftarrow \mathrm{D}(m, n / 2)$
si $(\mathrm{P}(m)=1)$ et $(\mathrm{P}(n)=1) \quad$ faire $\mathrm{D}(m, n) \leftarrow \mathrm{D}(\mathrm{A}(n)-\mathrm{A}(m), \mathrm{S}(m, n))$

Exercice 3

Soit

un entier naturel. On dit que c'est un 2 -palindrome si son écriture en base 2 est la même qu'elle soit écrite de gauche à droite ou de droite à gauche. Plus précisément, si

, avec

dans

est un 2-palindrome si

, pour tout entier

dans

. Par exemple, les entiers 3 (11), 5 (101), 7 (111), 9 (1001), et 15 (1111) sont des 2-palindromes. Ecrire un programme qui calcule les 2-palindromes

tels que

Exercice 4

On considère l'alphabet à deux lettres:

.
Dans toute la suite, on fixe

un mot non vide sur l'alphabet

; on note

la longueur de

(c'est à dire son nombre de lettres) et

ses

lettres lues de gauche à droite, c'est à dire que

.
Soit

un automate sur l'alphabet

défini par :

, l'ensemble des états de , est l'ensemble ,
, l'ensemble des transitions de , est l'ensemble :
1 est l'état initial de ,
est l'unique état final de .

On note

le langage reconnu par l'automate

On suppose que est la lettre . Donc .
(a) Représenter l'automate et justifier que est le langage des mots se terminant par un .
(b) Donner une expression rationnelle de .
(c) On considère l'automate représenté sur la figure 1 .

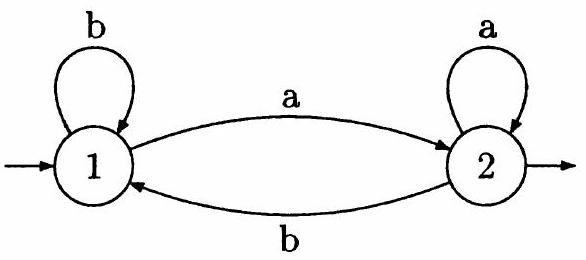
Figure 1: Automate

i. Démontrer que l'automate

est déterministe.
ii. Démontrer que le langage reconnu par l'automate

est égal à

.
2. On suppose ici que

et que les lettres de

sont toutes égales à

(

).
(a) Représenter l'automate

et décrire le langage

dans ce cas.

On se propose de déterminiser l'automate

On applique à

l'algorithme de déterminisation et on note

l'automate ainsi obtenu.
(b) Montrer que les états de

sont :

, et que les transitions de

sont alors :

({1}, ),
({1}, ,
, pour tout dans ,
, pour tout dans ,
.
(c) Quel est l'état initial de ?
(d) Quels sont les états finaux de ?
(e) Représenter .

On suppose que est pair et que lorsque est impair, lorsque est pair, c'est à dire que . Construire un automate déterministe qui reconnait l'ensemble des mots finis sur l'alphabet qui se terminent par .

Exercice 5

Soient trois fonctions booléennes. Justifier l'égalité : .
Une fonction booléenne est dite affine si elle se décompose comme une somme de variables. Par exemple, et sont des fonctions affines des variables . On considère la fonction booléenne des 5 variables , définie par :

Décomposer

comme un produit de fonctions booléennes affines (on pourra utiliser la question 1.).
3. Le directeur d'une banque souhaite, qu'en son absence, certains de ses collaborateurs, regroupés par deux ou trois selon un protocole établi précisément, puissent ouvrir le coffre. Pour cela, la porte du coffre est munie de

serrures et les

clés correspondantes sont nécessaires à l'ouverture de la porte. Le directeur dispose des clés des serrures en nombre suffisant et il en distribue certaines à ses collaborateurs de façon à ce que les seules possibilités soient :

Ulysse et Victoire peuvent à eux deux ouvrir le coffre
Victoire, Xavier et Yves peuvent à eux trois ouvrir le coffre,
Victoire, Xavier et Zoé peuvent à eux trois ouvrir le coffre,
Ulysse, Yves et Zoé peuvent à eux trois ouvrir le coffre.

Déterminer le nombre minimal de serrures du coffre et une distribution convenable des clés.