Version interactive avec LaTeX compilé
Les frottements de glissement
Diverses valeurs numériques sont regroupées à la fin de l'énoncé. On y trouvera aussi un formulaire fournissant quelques intégrales utiles et deux expressions d'analyse vectorielle.
Cet énoncé aborde quelques phénomènes associés aux frottements de deux solides
I Effets thermiques aux jonctions
Lorsque
I.A - Diffusion thermique dans un milieu semi-infini
On considère pour l'instant un solide indilatable, homogène et semi-infini, situé dans le domaine
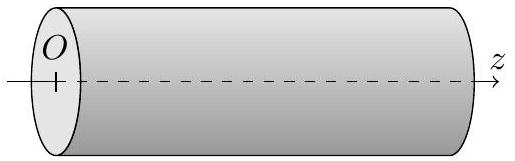
Figure 1
lieu, présentant préalablement une température uniforme
I.A.1) Montrer que l'élévation de température
I.A.1) Montrer que l'élévation de température
Que devient cette équation lorsque
I.A.2) Milieu chauffé brièvement
Dans cette question, le solide n'est chauffé que pendant une durée extrêmement brève entre les instants
a) Que vaut
b) On note
c) Exprimer la variation de l'énergie interne
d) Plaçons-nous maintenant dans la situation où le très bref échange thermique
a) Que vaut
b) On note
c) Exprimer la variation de l'énergie interne
d) Plaçons-nous maintenant dans la situation où le très bref échange thermique
I.A.3) Milieu chauffé continument
a) Le système est maintenant chauffé sans interruption à partir de l'instant initial avec une densité de flux thermique
Quelle quantité de chaleur
b) Dans le cas particulier où
Quelle quantité de chaleur
b) Dans le cas particulier où
où
Exprimer l'élévation de température
La profondeur
Exprimer l'élévation de température
La profondeur
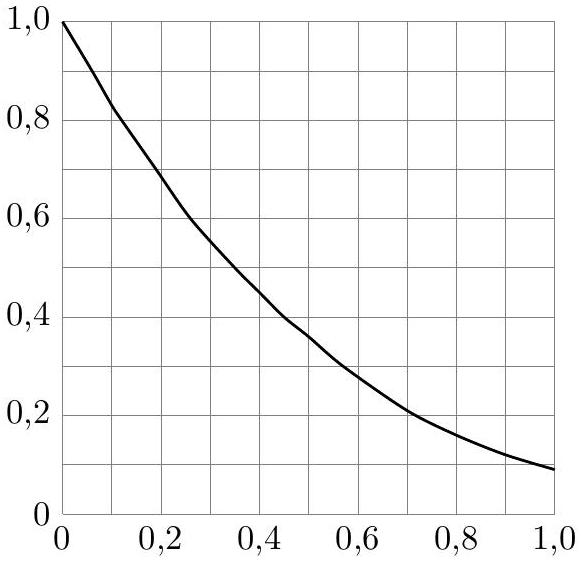
Figure 2 Graphe de la fonction
I.B - Production d'énergie thermique par les frottements
On étudie dorénavant la situation où deux cylindres
I.B.1) On note
I.B.2) Appliquer le premier principe à l'ensemble des deux solides.
I.B.3) En déduire une relation entre
I.B.1) On note
I.B.2) Appliquer le premier principe à l'ensemble des deux solides.
I.B.3) En déduire une relation entre
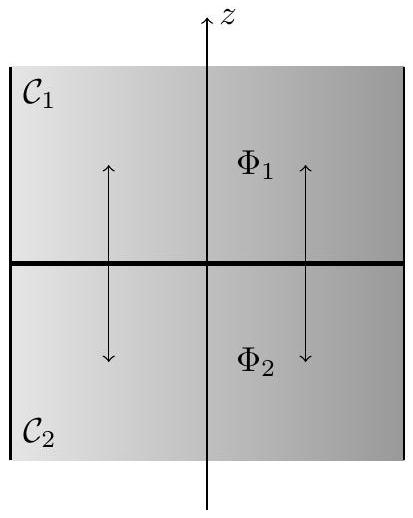
Figure 3
I.C - Application aux jonctions
Le modèle développé dans les questions précédentes permet d'estimer l'échauffement des jonctions décrites dans l'introduction lorsque
I.C.1) Quand
I.C.2) Les jonctions ont un diamètre de l'ordre de
I.C.3) Pour estimer les effets thermiques au niveau des jonctions, on utilise les résultats de I.A.3.b à l'instant
a) Comparer quantitativement les propriétés de l'acier, du granit et du Téflon en calculant l'élévation de température de l'interface et la profondeur
b) Analyser la pertinence de l'approximation qui consiste à supposer les deux milieux semi-infinis pour étudier la diffusion thermique dans chaque jonction (hypothèse introduite au début de I.A).
I.C.1) Quand
I.C.2) Les jonctions ont un diamètre de l'ordre de
I.C.3) Pour estimer les effets thermiques au niveau des jonctions, on utilise les résultats de I.A.3.b à l'instant
a) Comparer quantitativement les propriétés de l'acier, du granit et du Téflon en calculant l'élévation de température de l'interface et la profondeur
b) Analyser la pertinence de l'approximation qui consiste à supposer les deux milieux semi-infinis pour étudier la diffusion thermique dans chaque jonction (hypothèse introduite au début de I.A).
II Un système auto-lubrifié
Les forces de frottement associées au glissement d'un solide sur la glace ou la neige sont fréquemment étudiées en raison de leur importance pour diverses pratiques récréatives ou pour les moyens de transport dans les régions froides. À des températures de l'ordre de
Dans les parties II et III, il est question des forces s'exerçant sur
Dans les parties II et III, il est question des forces s'exerçant sur
II.A - Mécanisme de fusion
Deux hypothèses ont été émises pour expliquer la fusion superficielle de la glace:
- selon Reynolds, la fusion s'explique par la surpression exercée par le patin sur la glace ;
- selon Bowden, la fusion s'explique par l'élévation de température provoquée par les frottements.
Les questions ci-dessous apportent des éléments pour trancher parmi ces deux propositions.
II.A.1) Considérons une paire de skis d'aire apparente
II.A.2) Rappeler l'allure du diagramme d'état de l'eau dans le plan (
II.A.3) Considérons maintenant l'échauffement associé aux frottements pour un patin glissant à la vitesse
II.A.4) Pour un patin isolant, toute la chaleur produite par les frottements diffuse vers la glace. En utilisant le résultat de la question I.A.3.b, exprimer l'échauffement de la surface de la glace pendant la durée
II.A.5) Calculer numériquement le temps nécessaire à un échauffement de
II.A.6) L'expérience montre que les forces de frottement augmentent énormément si
II.A.1) Considérons une paire de skis d'aire apparente
II.A.2) Rappeler l'allure du diagramme d'état de l'eau dans le plan (
II.A.3) Considérons maintenant l'échauffement associé aux frottements pour un patin glissant à la vitesse
II.A.4) Pour un patin isolant, toute la chaleur produite par les frottements diffuse vers la glace. En utilisant le résultat de la question I.A.3.b, exprimer l'échauffement de la surface de la glace pendant la durée
II.A.5) Calculer numériquement le temps nécessaire à un échauffement de
II.A.6) L'expérience montre que les forces de frottement augmentent énormément si
II.B - Frottements visqueux et dissipation dans la couche lubrifiante
Au niveau d'une jonction entre la glace immobile et le patin de vitesse
II.B.1) Justifier que
II.B.2) Dans la situation étudiée ici, la force surfacique s'exerçant vers les
II.B.1) Justifier que
II.B.2) Dans la situation étudiée ici, la force surfacique s'exerçant vers les
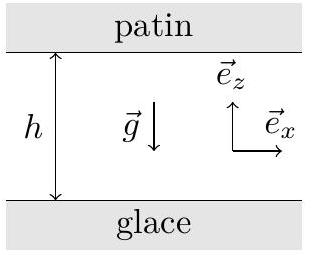
Figure 4
au travers d'une surface de cote
II.B.3) On rappelle l'équation de Navier-Stokes régissant la dynamique des fluides visqueux newtoniens :
II.B.3) On rappelle l'équation de Navier-Stokes régissant la dynamique des fluides visqueux newtoniens :
Aucun gradient de pression n'est appliqué selon
II.B.4) Exprimer la composante tangentielle
II.B.5) Exprimer la puissance
II.B.6) Pour une épaisseur de film
II.B.7) On considère le système fermé constitué par l'eau contenue à l'instant
a) Justifier que le travail des forces de pression sur ce système est nul.
b) Montrer que la puissance thermique sortant du système vaut
II.B.4) Exprimer la composante tangentielle
II.B.5) Exprimer la puissance
II.B.6) Pour une épaisseur de film
II.B.7) On considère le système fermé constitué par l'eau contenue à l'instant
a) Justifier que le travail des forces de pression sur ce système est nul.
b) Montrer que la puissance thermique sortant du système vaut
III Détermination de l'épaisseur de la couche lubrifiante
La détermination de l'épaisseur
III.A - Croissance du film d'eau contrôlée par les frottements seuls
Toute l'énergie thermique produite par la dissipation visqueuse avec la puissance calculée en II.B.7.b est supposée disponible pour la fusion de la glace. L'eau liquide formée, de masse volumique
Soit d
Soit d
III.B - Expulsion du film d'eau
En réalité, l'eau liquide présente dans les jonctions en est expulsée sous l'effet des forces verticales, ce qui limite la croissance du film lubrifiant. Dans toute la partie III.B, on se concentre sur ce phénomène d'expulsion pour évaluer la décroissance de
On adopte un modèle à symétrie cylindrique (figure 5), le patin et la glace étant assimilés près d'une jonction à des disques de diamètre
On adopte un modèle à symétrie cylindrique (figure 5), le patin et la glace étant assimilés près d'une jonction à des disques de diamètre
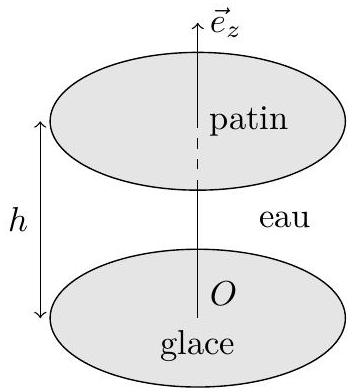
Figure 5
III.B.1) On procède à une analyse d'ordres de grandeurs pour résoudre l'équation de Navier-Stokes dont la projection sur
On note
a) En exploitant l'incompressibilité de l'écoulement, relier
b) Analyser l'ordre de grandeur des quatre termes diffusifs. Montrer numériquement que l'un est dominant. On néglige dans la suite les trois autres.
c) Montrer de la même manière qu'on peut négliger les termes convectifs devant celui associé aux forces visqueuses.
d) Faire de même pour le terme instationnaire proportionnel à
e) En déduire l'écriture simplifiée de l'équation III.1.
a) En exploitant l'incompressibilité de l'écoulement, relier
b) Analyser l'ordre de grandeur des quatre termes diffusifs. Montrer numériquement que l'un est dominant. On néglige dans la suite les trois autres.
c) Montrer de la même manière qu'on peut négliger les termes convectifs devant celui associé aux forces visqueuses.
d) Faire de même pour le terme instationnaire proportionnel à
e) En déduire l'écriture simplifiée de l'équation III.1.
Des analyses similaires, non demandées, permettent de montrer que les gradients axiaux de pression sont négligeables ce qui revient à considérer que
III.B.2) Exprimer le champ de vitesse
III.B.3) Exprimer le débit volumique
III.B.4) Relier d'autre part ce débit à
III.B.5) En déduire l'expression suivante du champ de pression :
III.B.2) Exprimer le champ de vitesse
III.B.3) Exprimer le débit volumique
III.B.4) Relier d'autre part ce débit à
III.B.5) En déduire l'expression suivante du champ de pression :
III.B.6) Calculer la résultante des forces de pression
III.B.7) Les termes indépendants de
III.B.8) Calculer numériquement
III.B.7) Les termes indépendants de
III.B.8) Calculer numériquement
III.C - Croissance isotherme du film d'eau limitée par expulsion
En poursuivant les calculs de III.B, on obtient une expression du débit expulsé de la jonction :
On reprend ici l'analyse des variations de
III.C.1) Montrer que dans ce modèle,
On reprend ici l'analyse des variations de
III.C.1) Montrer que dans ce modèle,
où
III.C.2) Exprimer la hauteur limite
III.C.3) Des résultats expérimentaux suggèrent qu'à des températures pas trop basses, la résultante des forces de frottement tangentielles exercées sur le patin est proportionnelle à
III.C.2) Exprimer la hauteur limite
III.C.3) Des résultats expérimentaux suggèrent qu'à des températures pas trop basses, la résultante des forces de frottement tangentielles exercées sur le patin est proportionnelle à
IV Frottement entre solides non lubrifiés
Lorsque deux solides glissent l'un contre l'autre sans couche liquide intermédiaire, les forces de frottement qu'ils exercent l'un sur l'autre présentent un comportement très différent de celui étudié dans les parties II et III. Pour les décrire, on conserve cependant les notations
Dès le XVII
Dès le XVII
-
est proportionnelle à , le facteur de proportionnalité dépendant de la nature des matériaux en contact ; -
est indépendante de la surface apparente de contact .
L'interprétation de ces observations date de 1950 environ et repose sur l'analyse des phénomènes ayant lieu au niveau des jonctions. En effet, ces jonctions se déforment sous l'effet des efforts perpendiculaires à l'interface et un contact intime s'y crée entre les deux solides. Pour déplacer les uns contre les autres les atomes de
Deux types de déformation des jonctions sont envisagés tour à tour dans la suite : les déformations plastiques d'une part et les déformations élastiques d'autre part.
Deux types de déformation des jonctions sont envisagés tour à tour dans la suite : les déformations plastiques d'une part et les déformations élastiques d'autre part.
IV.A - Cas des déformations plastiques
Dans ce premier cas, on admet que
IV.A.1) Quelle relation existe-t-il entre
IV.A.2) Calculer numériquement la valeur de
IV.A.3) En supposant qu'il y a glissement d'un solide sur l'autre et que toutes les jonctions glissent en même temps, établir le lien entre
IV.A.4) Cette modélisation permet-elle d'expliquer les deux propriétés introduites dans le préambule de la partie IV ? Pourquoi ?
IV.A.1) Quelle relation existe-t-il entre
IV.A.2) Calculer numériquement la valeur de
IV.A.3) En supposant qu'il y a glissement d'un solide sur l'autre et que toutes les jonctions glissent en même temps, établir le lien entre
IV.A.4) Cette modélisation permet-elle d'expliquer les deux propriétés introduites dans le préambule de la partie IV ? Pourquoi ?
IV.B - Cas des déformations élastiques
Dans ce second cas nous supposons pour simplifier que la surface de
où
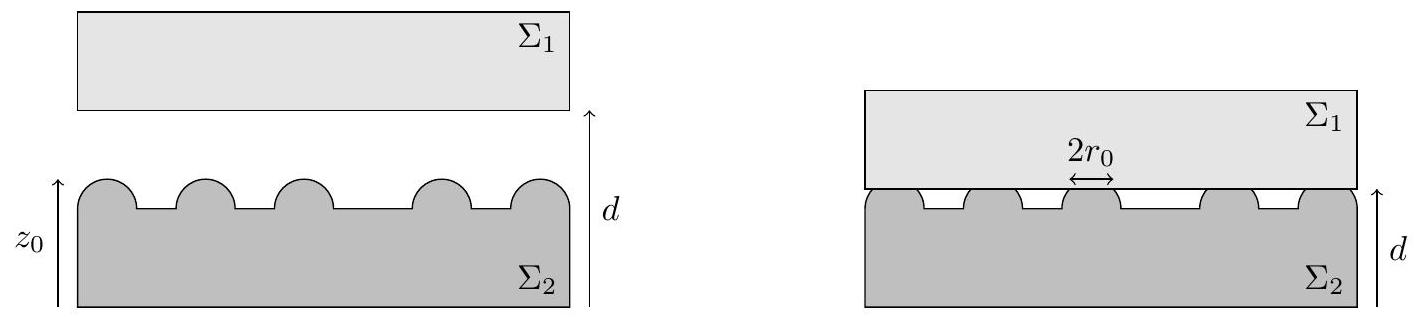
Figure 6 Contact sur une surface modélisée par une série de bosses sphériques
IV.B.1) Relier l'aire de contact
IV.B.2) Cette modélisation permet-elle d'expliquer les deux propriétés introduites dans le préambule de la partie IV? Pourquoi?
IV.B.3) En réalité, les sommets des aspérités de surface, ici représentées par les protubérances sphériques, ne se trouvent pas tous à la même hauteur avant le contact avec
a) Avec un nombre d'aspérités
b) Lorsque
c) Donner dans les mêmes conditions une expression intégrale de l'aire de contact
d) Faire de même pour
e) Fréquemment, la fonction
f) Le modèle de Greenwood permet-il d'expliquer les deux propriétés introduites dans le préambule de la partie IV ? Pourquoi ?
IV.B.2) Cette modélisation permet-elle d'expliquer les deux propriétés introduites dans le préambule de la partie IV? Pourquoi?
IV.B.3) En réalité, les sommets des aspérités de surface, ici représentées par les protubérances sphériques, ne se trouvent pas tous à la même hauteur avant le contact avec
a) Avec un nombre d'aspérités
b) Lorsque
c) Donner dans les mêmes conditions une expression intégrale de l'aire de contact
d) Faire de même pour
e) Fréquemment, la fonction
f) Le modèle de Greenwood permet-il d'expliquer les deux propriétés introduites dans le préambule de la partie IV ? Pourquoi ?
Données numériques
| Matériau |
|
|
|
|
| acier |
|
|
75 |
|
| granit |
|
|
2,2 |
|
| Téflon |
|
|
2,3 |
|
| cuivre |
|
|
|
|
| chêne |
|
|
0,2 | |
| glace |
|
|
2,3 |
Échelles de température :
Pression atmosphérique :
Coordonnées du point triple de l'eau:
Viscosité dynamique de l'eau à
Masse volumique de l'eau liquide:
Enthalpie massique de fusion de la glace
Dureté de l'acier:
Accélération de la pesanteur
Pression atmosphérique :
Coordonnées du point triple de l'eau:
Viscosité dynamique de l'eau à
Masse volumique de l'eau liquide:
Enthalpie massique de fusion de la glace
Dureté de l'acier:
Accélération de la pesanteur
Formulaire
En coordonnées cylindriques,
