Version interactive avec LaTeX compilé
Les données sont regroupées en fin d'énoncé. Les résultats numériques seront donnés avec un nombre de chiffres significatifs compatible avec celui utilisé pour les données.
Du minerai aux applications : le cuivre
Le cuivre est un des métaux les plus anciennement utilisés par l'homme (depuis sans doute dix millénaires), d'abord en parallèle avec des outils de pierre puis, allié à l'étain, sous forme de bronze, par exemple dans l'Égypte ancienne, à l'époque du sphinx et des pyramides de Gizeh. L'actualité a récemment mis en évidence la forte augmentation du cours commercial du cuivre : en effet, avec une production annuelle mondiale de l'ordre de 15 à 20 millions de tonnes, les réserves de minerai connues devraient être épuisées dans peu de temps.
Le cuivre a pris le nom de l'île de Chypre, où il fut d'abord extrait. Métal de couleur rouge, caractérisé par d'excellentes conductivités thermique et électrique, assez peu oxydable dans les conditions ordinaires de son emploi, le cuivre est aussi relativement peu toxique ; il est logiquement utilisé pour de nombreuses applications, pur ou sous forme d'alliage. Ce sujet illustre diverses étapes de la fabrication et de la caractérisation d'un élément métallique à base de cuivre, depuis l'extraction du minerai jusqu'à la caractérisation physico-chimique de la structure cristalline du métal fini.
Le cuivre a pris le nom de l'île de Chypre, où il fut d'abord extrait. Métal de couleur rouge, caractérisé par d'excellentes conductivités thermique et électrique, assez peu oxydable dans les conditions ordinaires de son emploi, le cuivre est aussi relativement peu toxique ; il est logiquement utilisé pour de nombreuses applications, pur ou sous forme d'alliage. Ce sujet illustre diverses étapes de la fabrication et de la caractérisation d'un élément métallique à base de cuivre, depuis l'extraction du minerai jusqu'à la caractérisation physico-chimique de la structure cristalline du métal fini.
Le problème comporte de nombreuses parties et questions indépendantes.
I Du minerai au métal
I.A - Un minerai de cuivre, la chalcopyrite
La chalcopyrite est un minerai mixte de cuivre et de fer qui constitue une des principales sources de la production industrielle de cuivre. La formule brute décrivant sa stœchiométrie est
I.A.1) Une analyse massique grossière du minerai montre qu'il est composé pour un peu plus d'un tiers de soufre et pour un peu moins d'un tiers de fer (proportions en masse,
I.A.2) La structure cristalline de la chalcopyrite peut être décrite à partir d'un réseau cubique à faces centrées d'ions sulfure
I.A.3) Dans la chalcopyrite, les ions du fer et du cuivre occupent respectivement chacun une certaine fraction des sites tétraédriques de la structure cubique à faces centrées formée par les ions sulfure. Quelle est cette proportion? Quelle est la coordinence des cations fer et cuivre dans cette structure ?
I.A.4) Avant l'étude détaillée de la structure du cristal de chalcopyrite (par diffraction de faisceaux de neutrons), deux structures concurrentes ont été proposées :
I.A.1) Une analyse massique grossière du minerai montre qu'il est composé pour un peu plus d'un tiers de soufre et pour un peu moins d'un tiers de fer (proportions en masse,
I.A.2) La structure cristalline de la chalcopyrite peut être décrite à partir d'un réseau cubique à faces centrées d'ions sulfure
I.A.3) Dans la chalcopyrite, les ions du fer et du cuivre occupent respectivement chacun une certaine fraction des sites tétraédriques de la structure cubique à faces centrées formée par les ions sulfure. Quelle est cette proportion? Quelle est la coordinence des cations fer et cuivre dans cette structure ?
I.A.4) Avant l'étude détaillée de la structure du cristal de chalcopyrite (par diffraction de faisceaux de neutrons), deux structures concurrentes ont été proposées :
- dans la structure (
), les ions du fer sont tous au nombre d'oxydation +III; - dans la structure (
), les ions du fer sont tous au nombre d'oxydation +II.
Quel est, dans chacun des deux cas, le nombre d'oxydation des ions du cuivre ?
On a en fait identifié la structure (
On a en fait identifié la structure (
I.B - Obtention du cuivre métallique
Le passage de la chalcopyrite au cuivre métallique peut être réalisé par plusieurs procédés. L'un d'eux débute par le grillage de la chalcopyrite, produisant des sulfures de cuivre solides
I.B.1) Écrire l'équation-bilan de la réaction passant de
I.B.1) Écrire l'équation-bilan de la réaction passant de
La réaction est menée industriellement sous une pression partielle d'oxygène
I.B.2) On se place dans le cadre de l'approximation d'Ellingham. Tracer le diagramme donnant la valeur, à l'équilibre chimique, de
I.B.3) Pour quelle pression partielle de
I.B.2) On se place dans le cadre de l'approximation d'Ellingham. Tracer le diagramme donnant la valeur, à l'équilibre chimique, de
I.B.3) Pour quelle pression partielle de
I.
Le procédé de synthèse du cuivre métallique se poursuit par électroraffinage : le cuivre Cu obtenu par la réaction précédente, qui contient encore diverses impuretés métalliques (fer Fe , zinc Zn , argent Ag ), est disposé dans une solution aqueuse électrolytique de sulfate de cuivre acidifiée et sert d'électrode (
Du fait de l'existence de la tension
I.C.1) La tension
I.C.2) Quelle masse maximale de cuivre peut-on espérer récupérer par heure de fonctionnement par mètre carré de surface d'électrode ? Sur quelle électrode récupère-t-on ce cuivre ?
I.C.3) À l'issue d'une telle opération, on cherche à récupérer et valoriser le fer, le zinc et l'argent qui étaient contenus dans l'électrode (
Du fait de l'existence de la tension
I.C.1) La tension
I.C.2) Quelle masse maximale de cuivre peut-on espérer récupérer par heure de fonctionnement par mètre carré de surface d'électrode ? Sur quelle électrode récupère-t-on ce cuivre ?
I.C.3) À l'issue d'une telle opération, on cherche à récupérer et valoriser le fer, le zinc et l'argent qui étaient contenus dans l'électrode (
II Le cuivre, conducteur de l'électricité
II.A - Modèle microscopique de la conduction électrique
C'est en tant que conducteur de l'électricité que le cuivre trouve la plupart de ses applications industrielles. On veut proposer dans cette question un modèle microscopique pour la bonne conductivité électrique du cuivre cristallin. Dans le cristal de cuivre, un unique électron périphérique par atome de cuivre est délocalisé sur l'ensemble du volume du cristal ; on notera
La conduction électrique est due au déplacement des électrons de conduction (masse
II.A.1) On étudie un électron qui a subi un choc à l'instant
II.A.2) On notera
II.A.3) En déduire l'expression de la conductivité électrique
II.A.4) À température ambiante,
II.A.5) À très haute fréquence
II.A.6) Les chocs des électrons de conduction sur les autres particules du matériau sont largement dus à l'agitation thermique des particules dans le volume du cristal. Expliquer brièvement si la conductivité électrique est une fonction croissante ou décroissante de la température
La conduction électrique est due au déplacement des électrons de conduction (masse
II.A.1) On étudie un électron qui a subi un choc à l'instant
II.A.2) On notera
II.A.3) En déduire l'expression de la conductivité électrique
II.A.4) À température ambiante,
II.A.5) À très haute fréquence
II.A.6) Les chocs des électrons de conduction sur les autres particules du matériau sont largement dus à l'agitation thermique des particules dans le volume du cristal. Expliquer brièvement si la conductivité électrique est une fonction croissante ou décroissante de la température
II.B - Caténaire d'alimentation ferroviaire
La bonne conductivité électrique du cuivre explique son emploi dans les fils de contact (caténaires) d'alimentation de puissance des locomotives, mais aussi dans les câbles de signalisation des installations ferroviaires. Du fait de l'augmentation spectaculaire du prix du métal, ces câbles font l'objet de vols fréquents.
Nous nous intéresserons ici à l'alimentation électrique d'une ligne TGV, en haute tension alternative à la fréquence
Nous nous intéresserons ici à l'alimentation électrique d'une ligne TGV, en haute tension alternative à la fréquence
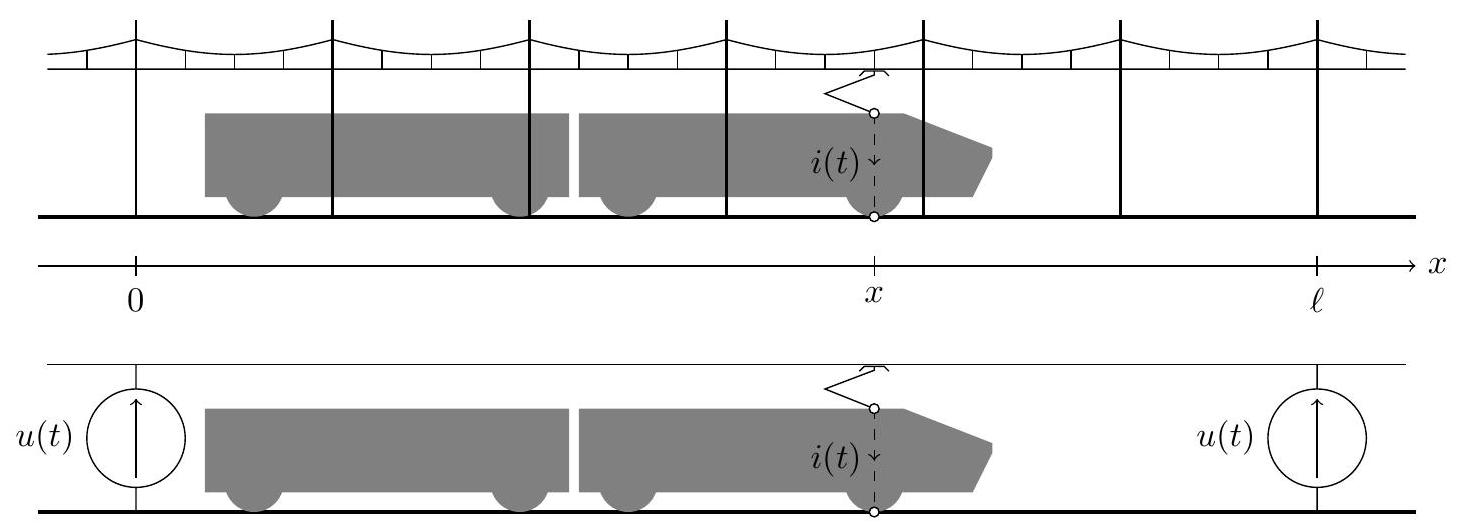
Figure 1 Caténaire d'alimentation ferroviaire
II.B.1) En fonctionnement normal, on mesure
Ces deux relations seront supposées vérifiées dans toute la suite.
II.B.2) On suppose que les valeurs du courant efficace et du facteur de puissance de la rame restent les mêmes ; montrer que la puissance moyenne consommée par la rame à l'abscisse
Application numérique.
Pour déterminer le meilleur choix économique lors de l'installation d'une ligne TGV, on prendra en compte le coût total annuel (amortissement en entretien compris) d'une sous-station (noté
II.B.3) Tous les poteaux de support ont les mêmes caractéristiques. Expliquez pourquoi le coût unitaire
II.B.4) Exprimer le coût total annuel de la ligne TGV, de longueur totale
Compte tenu de la valeur importante du courant efficace
II.B.5) Déterminer la valeur de la puissance moyenne qui peut être reçue par unité de longueur de caténaire en fonction de
II.B.6) Le coefficient surfacique de transfert conducto-convectif au niveau de la surface latérale est noté
Ces deux relations seront supposées vérifiées dans toute la suite.
II.B.2) On suppose que les valeurs du courant efficace et du facteur de puissance de la rame restent les mêmes ; montrer que la puissance moyenne consommée par la rame à l'abscisse
Application numérique.
Pour déterminer le meilleur choix économique lors de l'installation d'une ligne TGV, on prendra en compte le coût total annuel (amortissement en entretien compris) d'une sous-station (noté
II.B.3) Tous les poteaux de support ont les mêmes caractéristiques. Expliquez pourquoi le coût unitaire
II.B.4) Exprimer le coût total annuel de la ligne TGV, de longueur totale
Compte tenu de la valeur importante du courant efficace
II.B.5) Déterminer la valeur de la puissance moyenne qui peut être reçue par unité de longueur de caténaire en fonction de
II.B.6) Le coefficient surfacique de transfert conducto-convectif au niveau de la surface latérale est noté
III La structure du cristal de cuivre
L'analyse de la structure cristalline des métaux comme le cuivre est réalisée par des expériences de diffraction, soit de faisceaux de rayon
III.A - Diffraction par un cristal
III.A.1) Proposer un ordre de grandeur de la longueur d'onde
III.A.2) La longueur d'onde
III.A.3) Expliquer ce qui, à votre avis, justifie ce choix des valeurs de
III.A.2) La longueur d'onde
III.A.3) Expliquer ce qui, à votre avis, justifie ce choix des valeurs de
III.B - Production d'un faisceau polychromatique de rayons
La conduite d'études de plus en plus détaillées de structures cristallines par diffraction des rayons X a nécessité la mise au point de sources de rayons X monochromatiques et très intenses, mais de longueur d'onde réglable. Une telle source est constituée par l'accélérateur de particules SOLEIL (Source Optimisée de Lumière d'Énergie Intermédiaire au Laboratoire). Dans cet accélérateur, des électrons (charge
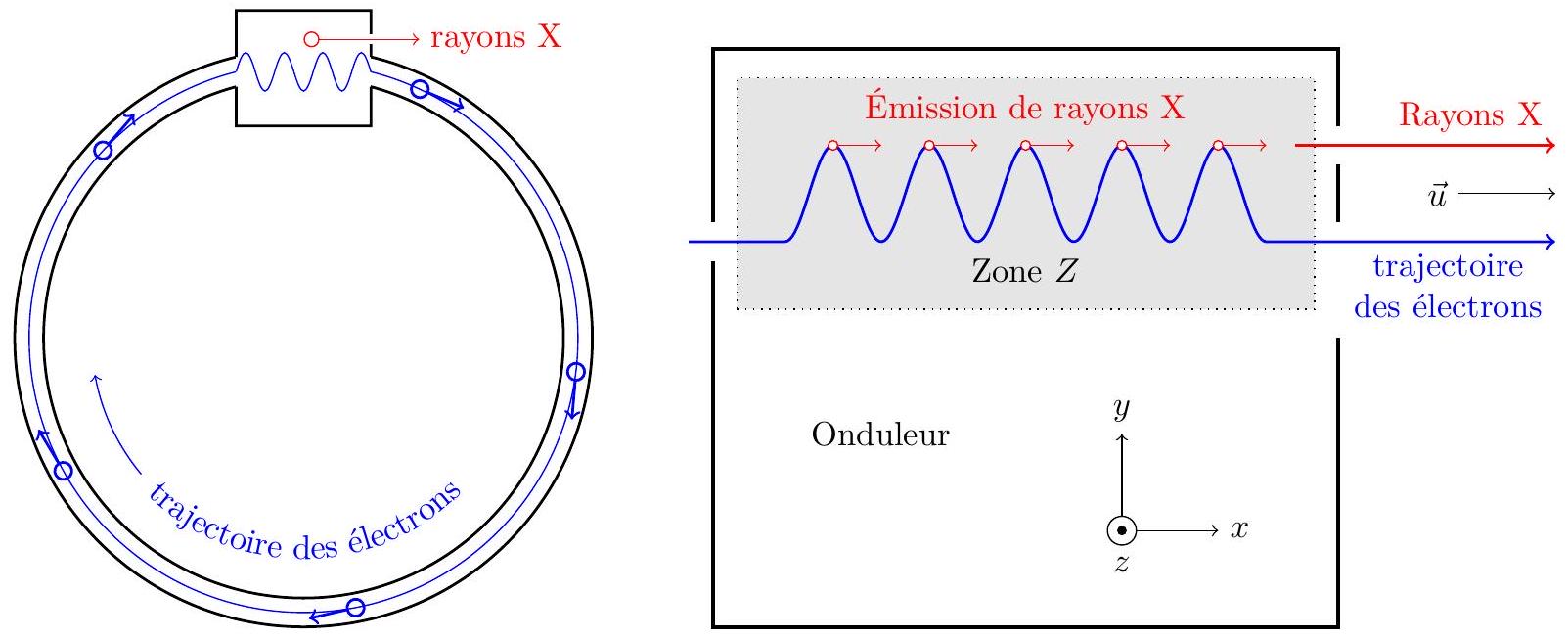
Figure 2 Schéma général du synchrotron SOLEIL (à gauche) et d'un onduleur (à droite)
III.B.1) Préciser, sur un schéma clair, le sens du champ magnétostatique
Application numérique. En admettant que la relation établie ci-dessus reste vraie pour
Application numérique. En admettant que la relation établie ci-dessus reste vraie pour
Un électron entre dans l'onduleur à la vitesse
III.B.2) Exprimer le principe fondamental de la dynamique pour un électron.
III.B.2) Exprimer le principe fondamental de la dynamique pour un électron.
Dans toute la suite, on suppose
Montrer que la trajectoire de l'électron dans le référentiel du laboratoire est sinusoïdale et déterminer les caractéristiques (amplitude et période) de cette sinusoïde.
Montrer que la trajectoire de l'électron dans le référentiel du laboratoire est sinusoïdale et déterminer les caractéristiques (amplitude et période) de cette sinusoïde.
On rappelle qu'une particule chargée accélérée rayonne un champ électromagnétique proportionnel à son accélération. C'est le cas de l'électron qui traverse l'onduleur. Cet électron a une vitesse
- exclusivement aux points où son accélération est maximale, donc où son déplacement transversal
est extrémal ; - dans la direction
de sa vitesse à l'instant d'émission ; - et que les rayonnements qu'il émet en tous les maximums de sa trajectoire (cf. figure 2 à droite) sont en phase. Par conséquent, ces rayonnements interfèrent constructivement à l'infini.
Ainsi l'onde émise par l'électron et qui se propage dans l'onduleur dans la directionest en phase avec les passages de l'électron aux maximums de sa trajectoire.
III.B.3) En utilisant cette dernière propriété, exprimer la longueur d'ondede cette onde électromagnétique en fonction de et d'un nombre entier et montrer que .
Exprimeren fonction de et de (on rappelle que ).
Calculer numériquementpour et et montrer qu'on a ainsi réalisé une source polychromatique de rayons X .
IV Étude thermodynamique d'un alliage du cuivre
Les alliages de cuivre Cu et de nickel Ni (cupronickels), très résistants à la corrosion, ont été utilisés depuis très longtemps, notamment pour la production de pièces de monnaie (voir figure 3), mais aussi pour des applications en construction navale. Cet alliage présente la particularité d'une miscibilité complète des deux métaux l'un dans l'autre, à l'état liquide mais aussi à l'état solide (les deux métaux cristallisent dans le même système cubique à faces centrées, et présentent des rayons atomiques voisins).

Figure 3 Pièces de monnaie (grecque antique et suisse moderne) en cupronickel (
Les masses molaires atomiques de ces deux éléments sont notées
IV.A - Potentiels chimiques dans des solutions idéales
IV.A.1) La solution liquide de nickel et de cuivre est considérée comme une solution idéale ; on note
IV.A.2) On note aussi
IV.A.2) On note aussi
et on précisera la fonction
IV.A.3) On note enfin
IV.A.3) On note enfin
IV.B - Fusion d'alliages de cupronickel
IV.B.1) On étudie à la température
IV.B.2) Une étude expérimentale de la fusion d'alliages de cupronickel permet la mesure, sous 1 bar et pour plusieurs compositions différentes de l'alliage solide, des températures de début de fusion
IV.B.2) Une étude expérimentale de la fusion d'alliages de cupronickel permet la mesure, sous 1 bar et pour plusieurs compositions différentes de l'alliage solide, des températures de début de fusion
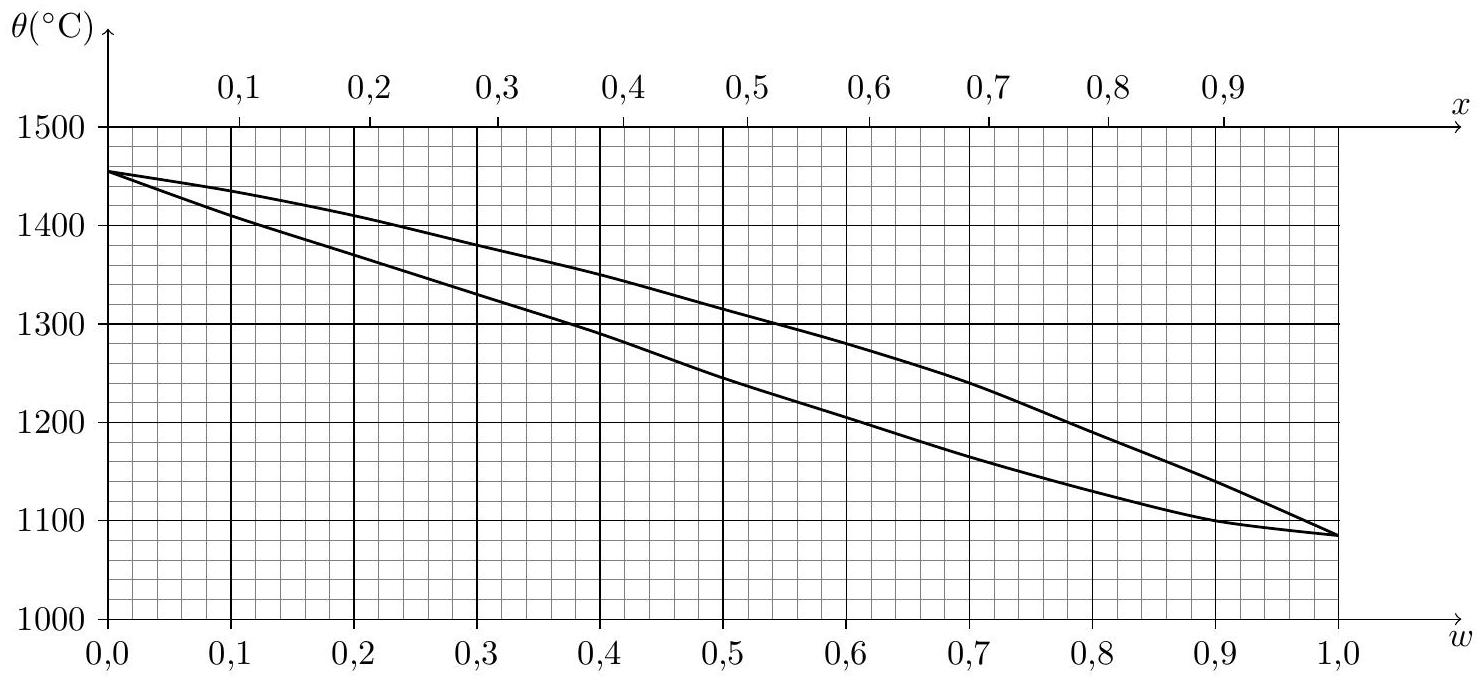
Figure 4 Fusion d'un alliage de cupronickel
IV.B.3) On considère une masse
On choisit une température égale à
On choisit une température égale à
IV.C - Grandeurs caractéristiques de fusion du cuivre
IV.C.1) À partir du diagramme figure 4, déterminer les températures absolues de fusion sous 1 bar du nickel pur
IV.C.2) Pour une transformation physico-chimique caractérisée par les grandeurs standard de réaction
IV.C.3) On considère l'équilibre entre une phase solide de cupronickel (fraction massique de cuivre
IV.C.2) Pour une transformation physico-chimique caractérisée par les grandeurs standard de réaction
IV.C.3) On considère l'équilibre entre une phase solide de cupronickel (fraction massique de cuivre
où le coefficient
IV.C.4) En expliquant soigneusement la méthode adoptée et les mesures effectuées, déduire des courbes de la figure 4 une estimation des valeurs numériques des enthalpie et entropie molaires de fusion
Ces valeurs diffèrent assez sensiblement de celles usuellement tabulées à partir de mesures relatives au cuivre pur. Pouvez-vous proposer une explication à cet écart ?
IV.C.4) En expliquant soigneusement la méthode adoptée et les mesures effectuées, déduire des courbes de la figure 4 une estimation des valeurs numériques des enthalpie et entropie molaires de fusion
Ces valeurs diffèrent assez sensiblement de celles usuellement tabulées à partir de mesures relatives au cuivre pur. Pouvez-vous proposer une explication à cet écart ?
Données numériques
- Propriétés des éléments et matériaux soufre, fer et cuivre.
| Soufre | Numéro atomique |
|
| Masse molaire atomique |
|
|
| Fer | Numéro atomique |
|
| Masse molaire atomique |
|
|
| Masse volumique (
|
|
|
| Cuivre | Numéro atomique |
|
| Masse molaire atomique |
|
|
| Masse volumique (
|
|
- Grandeurs physiques et constantes universelles.
| Masse d'un électron |
|
| Masse d'un neutron |
|
| Charge élémentaire |
|
|
|
|
| Constante d'Avogadro |
|
| Constante de Planck |
|
| Célérité de la lumière dans le vide |
|
| Perméabilité magnétique du vide |
|
| Constante molaire des gaz parfaits |
|
| Constante de Boltzmann |
|
| Accélération de la pesanteur |
|
- Données thermodynamiques : enthalpies de formation, entropies molaires standard à 298 K .
| Espèce chimique | État |
|
|
| Cu | solide | +33 | |
|
|
solide | -80 | +121 |
|
|
gaz | +205 | |
|
|
gaz | -297 | +248 |
- Données électrochimiques : potentiels standard à 298 K .
| Couple rédox |
|
Couple rédox |
|
|
|
|
|
|
|
|
|
|
|
