Version interactive avec LaTeX compilé
Quelques facettes d'un aquarium
Dans le but de sensibiliser le grand public à l'importance de la sauvegarde de la biodiversité et le respect de l'environnement,on peut visiter de nombreux aquariums dans le monde.Ils sont également importants en recherche,par exemple,dans le cadre de la survie des récifs coralliens.
Ce sujet comporte 3 parties indépendantes et propose d'étudier :
-la vidange et l'approvisionnement en eau de mer d'un aquarium ;
-le contrôle de la qualité de l'eau de l'aquarium ;
-les déperditions thermiques à travers les parois de l'aquarium ;
Toutes les réponses doivent être dûment justifiées.Les résultats doivent être encadrés.La qualité de la rédaction, a précision des raisonnements et le soin apporté à la copie sont des éléments d'évaluation de la composition du candidat.
Un ensemble de données,nécessaires à la résolution du problème,sont regroupées en fin d'énoncé.
Certaines questions,peu ou pas guidées,demandent de l'initiative de la part du candidat.Leur énoncé est repéré par une barre en marge.Il est alors demandé d'expliciter clairement la démarche et les choix effectués et de les illustrer,le cas échéant,par un schéma.Le barème valorise la prise d'initiative et tient compte du temps nécessaire à la résolution de ces questions.
Certaines données et formules utiles sont regroupées en fin d'énoncé.
Ce sujet comporte 3 parties indépendantes et propose d'étudier :
-la vidange et l'approvisionnement en eau de mer d'un aquarium ;
-le contrôle de la qualité de l'eau de l'aquarium ;
-les déperditions thermiques à travers les parois de l'aquarium ;
Toutes les réponses doivent être dûment justifiées.Les résultats doivent être encadrés.La qualité de la rédaction, a précision des raisonnements et le soin apporté à la copie sont des éléments d'évaluation de la composition du candidat.
Un ensemble de données,nécessaires à la résolution du problème,sont regroupées en fin d'énoncé.
Certaines questions,peu ou pas guidées,demandent de l'initiative de la part du candidat.Leur énoncé est repéré par une barre en marge.Il est alors demandé d'expliciter clairement la démarche et les choix effectués et de les illustrer,le cas échéant,par un schéma.Le barème valorise la prise d'initiative et tient compte du temps nécessaire à la résolution de ces questions.
Certaines données et formules utiles sont regroupées en fin d'énoncé.
I Vidange et approvisionnement en eau de mer d'un aquarium
I.A-Vidange d'un aquarium
Q 1.On souhaite vidanger par gravité un aquarium cubique d'arête
I.B-Pompage de l'eau de mer
Pour s'approvisionner en eau peu polluée,un musée puise cette ressource dans la mer à une profondeur de 50 m pour l'acheminer jusqu'à une citerne.
On choisit pour le repérage des altitudes un axe vertical ascendant(
On choisit pour le repérage des altitudes un axe vertical ascendant(
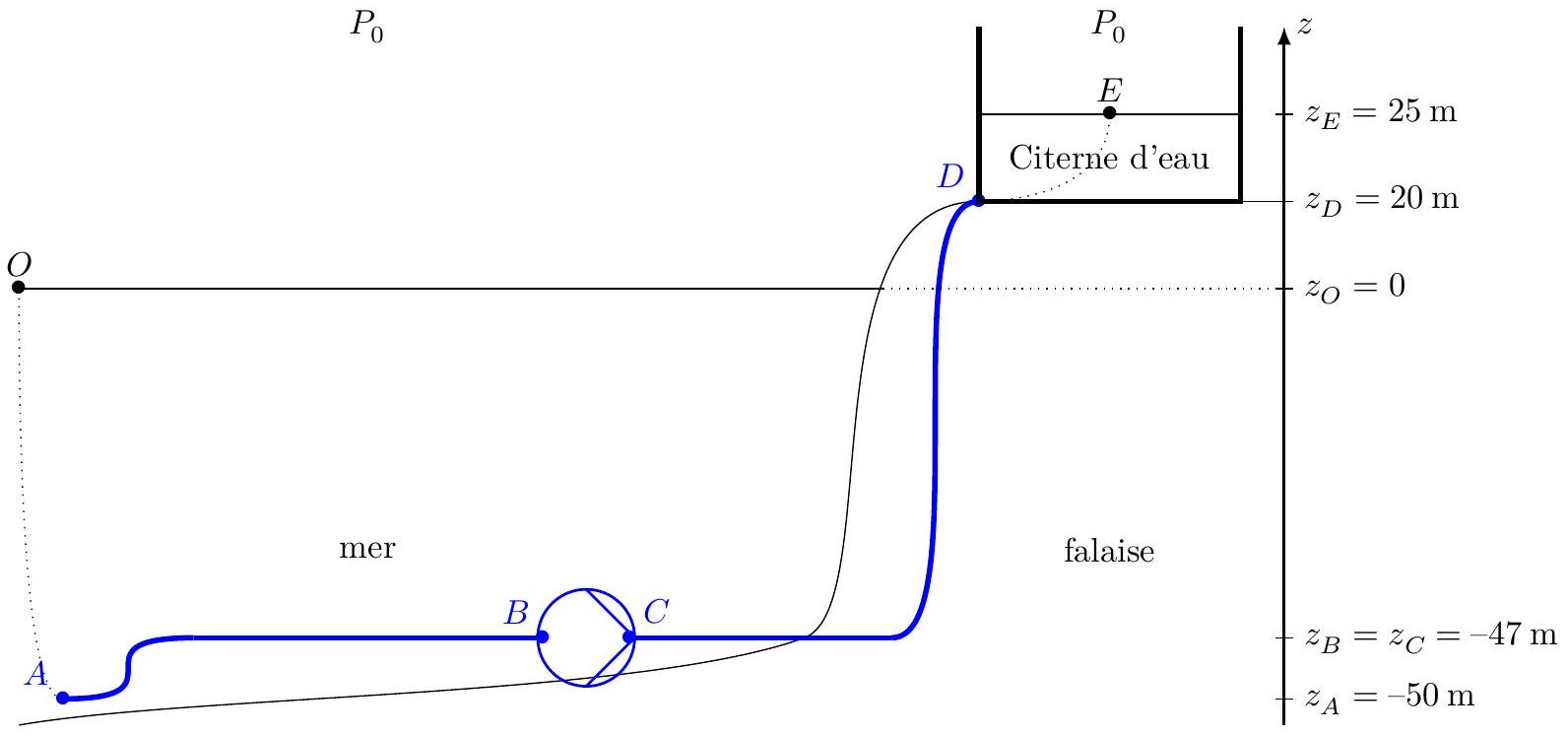
Figure 1 Pompage de l'eau de mer
Une pompe immergée fonctionne en permanence avec un débit volumique
On appelle circuit d'aspiration le tuyau reliant le point
On appelle circuit de refoulement le tuyau reliant le point
Le remplissage de la citerne se fait au point
On appelle circuit d'aspiration le tuyau reliant le point
On appelle circuit de refoulement le tuyau reliant le point
Le remplissage de la citerne se fait au point
avec
avec
Q 2. Aurait-il été possible de positionner la pompe au point
Q 3. Calculer
Q 4. Calculer Re, le nombre de Reynolds associé à l'écoulement de l'eau dans les canalisations. En déduire la nature du régime d'écoulement.
Q 5. En expliquant la démarche, déduire à l'aide du diagramme de Moody (figure 7), le coefficient de pertes de charge régulières
Q 6. Proposer une expérience permettant de mettre en évidence le phénomène de pertes de charge régulières.
Q 7. Calculer les pertes de charge régulières dans le tuyau d'aspiration
Q 8. Déterminer les expressions puis les valeurs des pertes de charge singulières dans le tuyau d'aspiration
Q 9. Rappeler les hypothèses nécessaires à l'application de la relation de Bernouilli.
Q 10. Déterminer l'expression de la différence de pression
Q 11. Déterminer l'expression de la différence de pression
Q 12. En déduire la puissance mécanique
Q 2. Aurait-il été possible de positionner la pompe au point
Q 3. Calculer
Q 4. Calculer Re, le nombre de Reynolds associé à l'écoulement de l'eau dans les canalisations. En déduire la nature du régime d'écoulement.
Q 5. En expliquant la démarche, déduire à l'aide du diagramme de Moody (figure 7), le coefficient de pertes de charge régulières
Q 6. Proposer une expérience permettant de mettre en évidence le phénomène de pertes de charge régulières.
Q 7. Calculer les pertes de charge régulières dans le tuyau d'aspiration
Q 8. Déterminer les expressions puis les valeurs des pertes de charge singulières dans le tuyau d'aspiration
Q 9. Rappeler les hypothèses nécessaires à l'application de la relation de Bernouilli.
Q 10. Déterminer l'expression de la différence de pression
Q 11. Déterminer l'expression de la différence de pression
Q 12. En déduire la puissance mécanique
II Contrôle de la qualité de l'eau de l'aquarium
II.A - Étude préliminaire de diagrammes
La figure 2 ci-dessous représente plusieurs diagrammes E-pH superposés.
- le diagramme
de l'élément manganèse, représenté en ligne pleine, est limité aux espèces chimiques suivantes: et ; - le diagramme
simplifié de l'élément iode, représenté en tirets, est limité aux espèces chimiques suivantes: et ; - le diagramme E-pH de l'eau est tracé en pointillés.
Pour les diagramme E-pH des éléments manganèse et iode, la convention de tracé utilisée est la suivante : sur une frontière, seules les deux formes du couple oxydant-réducteur sont considérées et chaque espèce dissoute contenant le manganèse (ou l'iode) a une concentration de valeur égale à
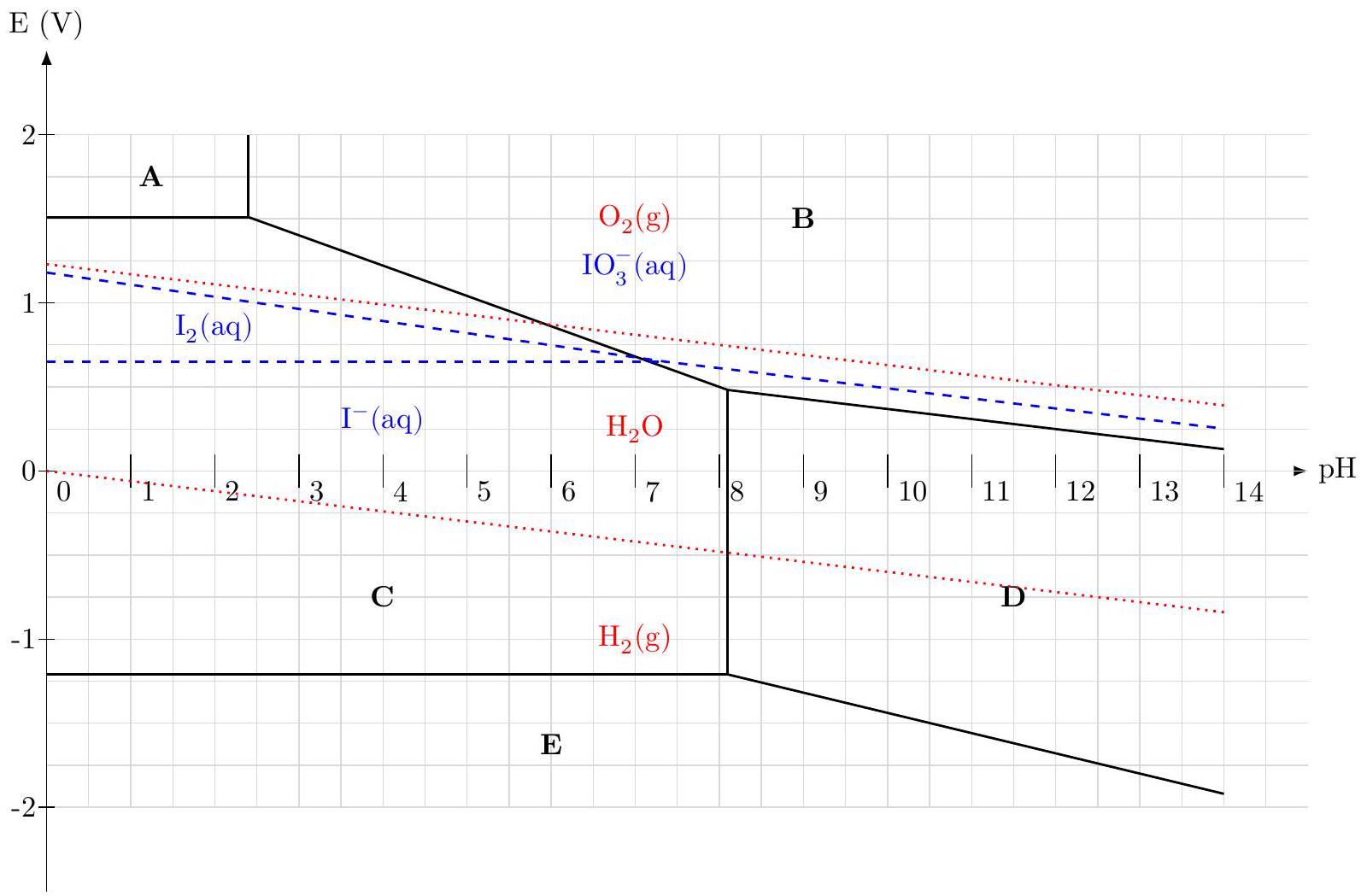
Figure 2 Diagrammes E-pH simplifiés de l'élément manganèse (en ligne pleine), de l'élément iode (en tirets) et de l'eau (en pointillés)
Q 13. Pour chacun des deux couples oxydant-réducteur de l'eau, préciser quelle espèce chimique est l'oxydant et laquelle est le réducteur.
Q 14. Déterminer le nombre d'oxydation de l'élément manganèse dans l'hydroxyde de manganèse (II)
Q 15. Attribuer, en justifiant la réponse, les différents domaines du diagramme E-pH de l'élément manganèse, repérés par les lettres
Q 16. En utilisant les diagrammes
Q 14. Déterminer le nombre d'oxydation de l'élément manganèse dans l'hydroxyde de manganèse (II)
Q 15. Attribuer, en justifiant la réponse, les différents domaines du diagramme E-pH de l'élément manganèse, repérés par les lettres
Q 16. En utilisant les diagrammes
II.B - Dosage du dioxygène dissous dans l'eau par la méthode de Winkler
Pour déterminer la concentration en dioxygène dissous dans l'eau, on utilise la méthode de Winkler dont le protocole est décrit ci-après :
Protocole
- Étape 1 : placer
de chlorure de manganèse (II), de la soude en excès sous forme de pastilles solides et un barreau aimanté dans un erlenmeyer de 250 mL . Dans un grand cristallisoir, remplir l'erlenmeyer à ras bord avec l'eau à analyser (le cristallisoir permet de prévenir tout débordement de la solution). Boucher rapidement l'erlenmeyer et éviter de maintenir de l'air à l'intérieur. - Étape 2 : agiter jusqu'à dissolution complète des réactifs et attendre environ trente minutes. On observe un précipité brun.
- Étape 3 : peser 3 g d'iodure de potassium. Verser le contenu de l'erlenmeyer dans un grand bécher contenant de l'acide sulfurique concentré et ajouter très rapidement les 3 g d'iodure de potassium (l'ajout d'acide sulfurique permet de ramener le pH de la solution à une valeur voisine de 1). Homogénéiser et agiter jusqu'à disparition totale du précipité brun et persistance d'une couleur jaune limpide.
Étape 4 : prélever un volumede la solution et la doser avec une solution de thiosulfate de sodium de concentration . Un indicateur coloré indique la fin du dosage.
Q 17. Expliquer pourquoi il est nécessaire de se placer initialement (étapes 1 et 2 du protocole) en milieu fortement basique. On pourra justifier la réponse en prenant appui sur les diagrammes
Q 19. Écrire les équations qui modélisent les transformations chimiques qui interviennent lors du passage en milieu acide et de l'ajout d'iodure de potassium (étape 3 du protocole). On pourra justifier la réponse en prenant appui sur les diagrammes E-pH de la figure 2.
Q 20. Expliquer pourquoi l'iodure de potassium est ajouté en large excès.
Q 21. L'équation de la réaction support du titrage qui intervient lors de l'étape 4 est la suivante :
Q 20. Expliquer pourquoi l'iodure de potassium est ajouté en large excès.
Q 21. L'équation de la réaction support du titrage qui intervient lors de l'étape 4 est la suivante :
En déduire que la concentration en dioxygène dissous dans l'eau analysée, exprimée en
où
Q 22. Exprimer, en micromoles par kilogramme d'eau, la valeur de la concentration
Q 23. Commenter la valeur de la concentration obtenue à la question 22 au regard de la figure 3 et sachant qu'on considère que la vie marine devient difficile lorsque la valeur de la concentration en dioxygène dissous devient inférieure à 90 micromoles de dioxygène par kilogramme d'eau.
Q 22. Exprimer, en micromoles par kilogramme d'eau, la valeur de la concentration
Q 23. Commenter la valeur de la concentration obtenue à la question 22 au regard de la figure 3 et sachant qu'on considère que la vie marine devient difficile lorsque la valeur de la concentration en dioxygène dissous devient inférieure à 90 micromoles de dioxygène par kilogramme d'eau.
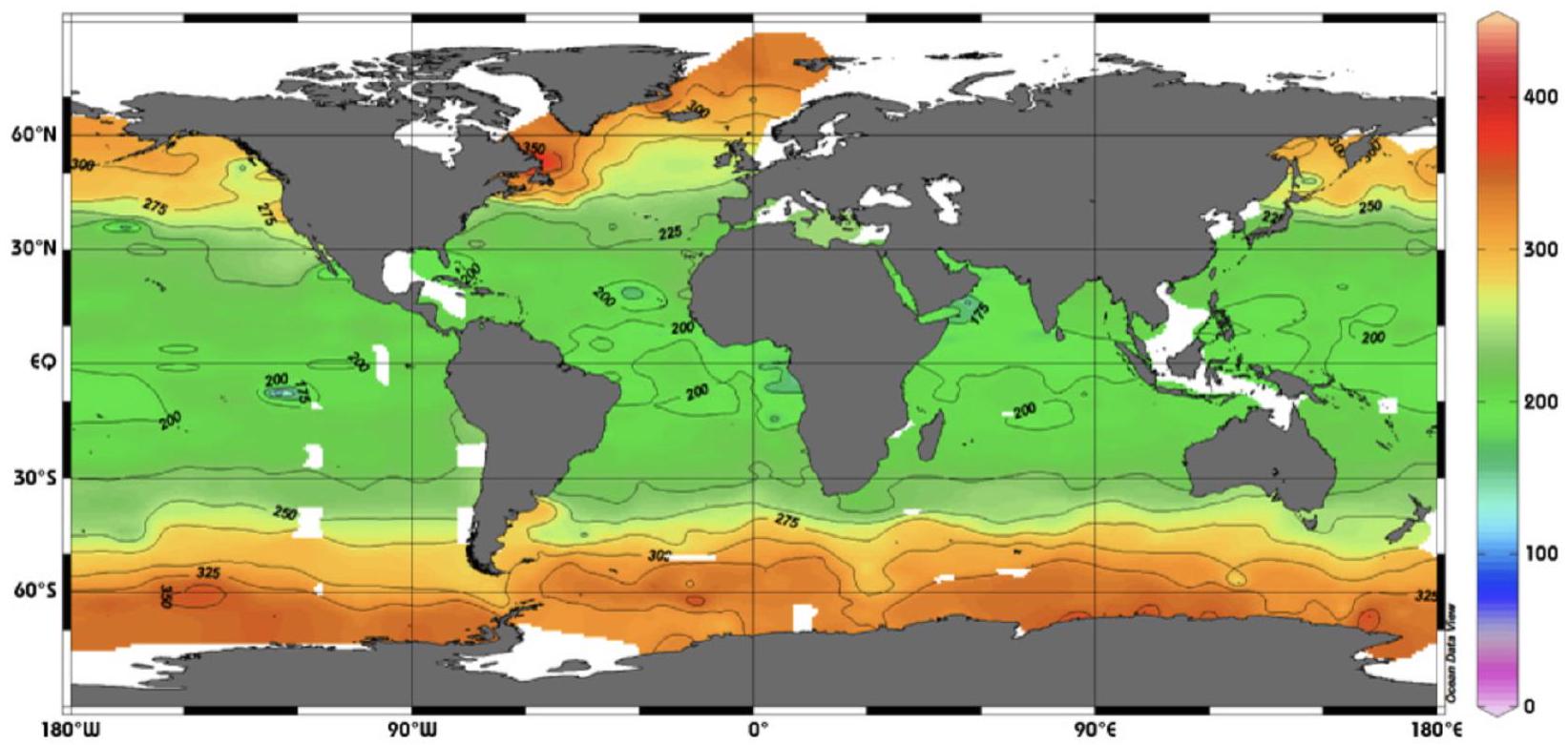
Figure 3 Concentration en dioxygène dissous dans les eaux de surface océaniques. L'échelle à droite de la figure indique les valeurs de concentration en micromoles de dioxygène par kilogramme d'eau (données eWOCE - https://www.ewoce.org/)
III Déperditions thermiques à travers les parois de l'aquarium
On considère un aquarium cubique ayant une longueur d'arête
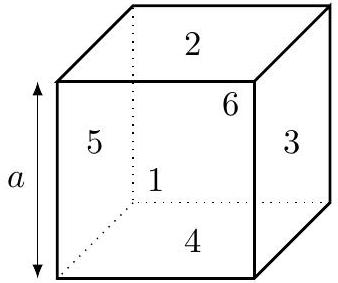
Figure 4 Numérotation des faces de l'aquarium
III.A - Renouvellement de l'eau
Dans un premier temps, on s'intéresse uniquement à la paroi 1 de l'aquarium. Elle est constituée de verre d'épaisseur
L'eau issue de la citerne d'approvisionnement est à la température initiale
On suppose que le flux thermique dans la paroi de verre s'effectue totalement dans la direction
L'eau issue de la citerne d'approvisionnement est à la température initiale
On suppose que le flux thermique dans la paroi de verre s'effectue totalement dans la direction
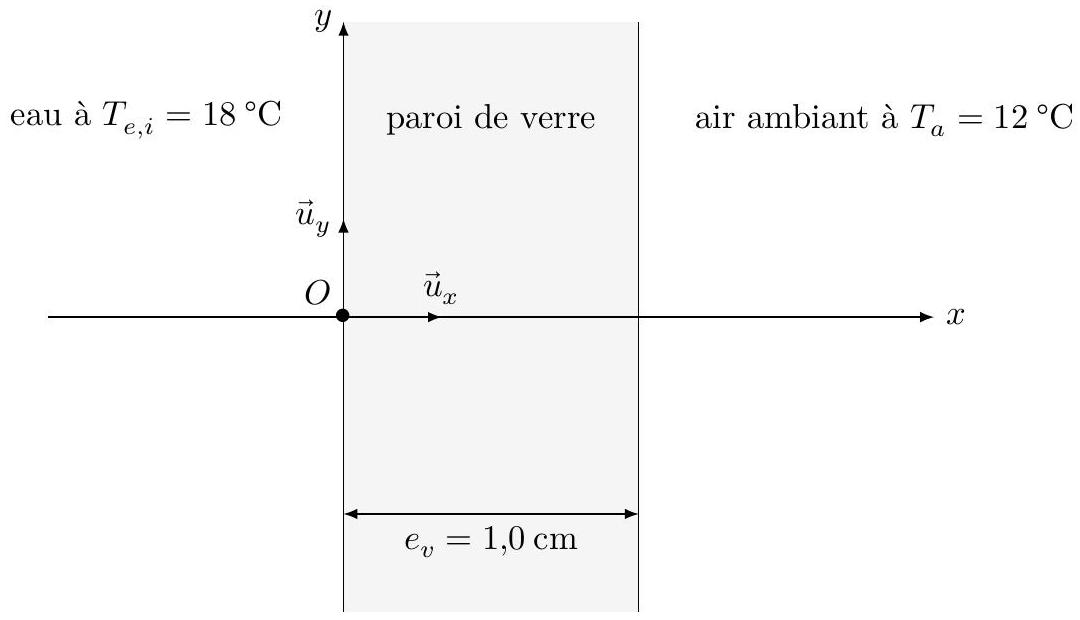
Figure 5 Représentation de la paroi 1
Q 24. Justifier que le vecteur densité de flux thermique ne dépende que de la coordonnée
Q 25. Comment appelle-t-on le coefficient
Q 26. Exprimer la durée
Q 26. Exprimer la durée
III.B - Régime stationnaire
On se place désormais dans le cas où le régime stationnaire est atteint.
Q 27. Déterminer l'évolution de la température
Q 28. Donner une représentation graphique de
Q 27. Déterminer l'évolution de la température
Q 28. Donner une représentation graphique de
III.C - Pertes de puissance thermique
Les poissons de cet aquarium ont besoin d'une température d'eau constante
III.C.1) Pertes par conduction thermique
On suppose que les autres parois (
On ne tient compte dans cette section que du transfert thermique par conduction.
Q 29. En raisonnant sur une analogie électrique, exprimer la résistance thermique de conduction
On s'intéresse à une seule des cinq parois modélisées par une couche de tartre et une couche de béton.
Q 30. Déterminer l'expression puis la valeur de la résistance thermique de conduction
On ne tient compte dans cette section que du transfert thermique par conduction.
Q 29. En raisonnant sur une analogie électrique, exprimer la résistance thermique de conduction
On s'intéresse à une seule des cinq parois modélisées par une couche de tartre et une couche de béton.
Q 30. Déterminer l'expression puis la valeur de la résistance thermique de conduction
III.C.2) Prise en compte de pertes convectives et du rayonnement
Les transferts convectifs entre la paroi de béton et l'air sont modélisés par la loi de Newton donnant le flux convectif
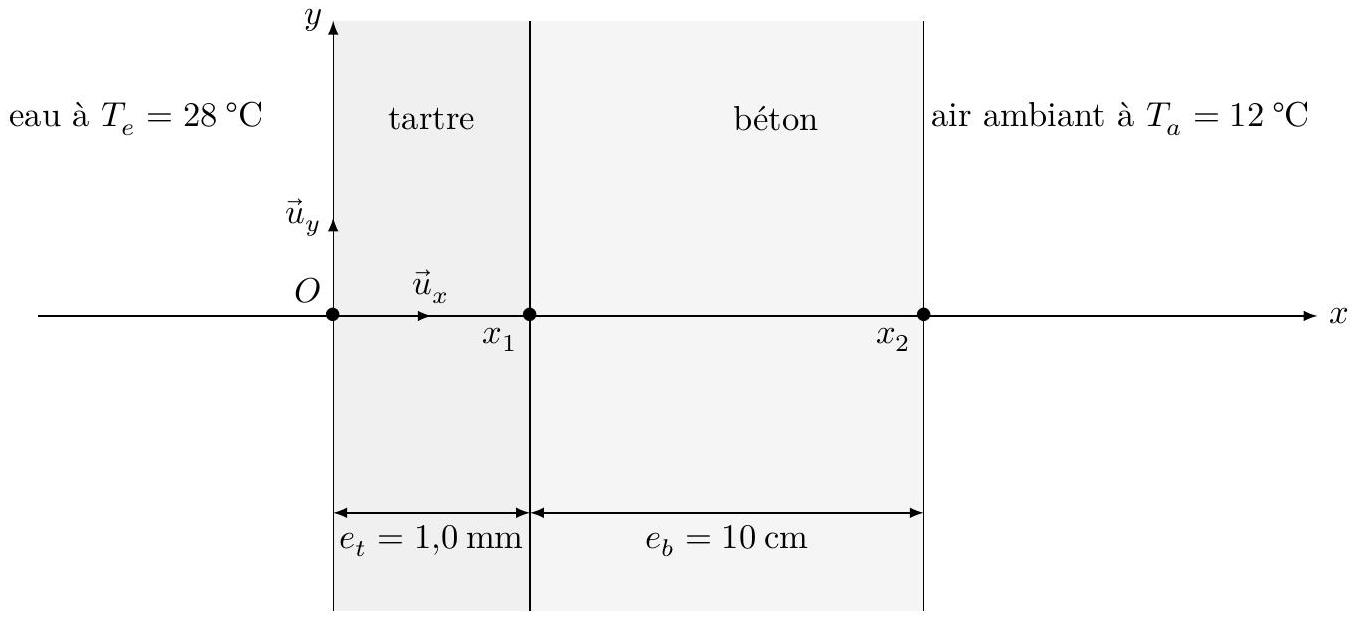
Figure 6 Représentation des parois 2 à 6
où
On note
Le transfert thermique par rayonnement entre la paroi de béton et l'extérieur est modélisé par le flux de rayonnement total
On note
Le transfert thermique par rayonnement entre la paroi de béton et l'extérieur est modélisé par le flux de rayonnement total
où
On note
Q 31. Pour une seule des cinq parois modélisées par une couche de tartre et une couche de béton, exprimer
Q 32. Pour une seule des cinq parois modélisées par une couche de tartre et une couche de béton, exprimer la résistance thermique
Q 33. On suppose que la température du tartre à l'interface eau-tartre est égale à celle de l'eau
On note
Q 31. Pour une seule des cinq parois modélisées par une couche de tartre et une couche de béton, exprimer
Q 32. Pour une seule des cinq parois modélisées par une couche de tartre et une couche de béton, exprimer la résistance thermique
Q 33. On suppose que la température du tartre à l'interface eau-tartre est égale à celle de l'eau
III.C.3) Bilan des pertes thermiques
Q 34. Calculer la résistance thermique de la paroi de verre 1 en tenant compte des transferts thermiques par conduction, convection et rayonnement. On donne, pour l'interface verre-air,
Q 35. Estimer la puissance thermique perdue à travers l'ensemble des parois de l'aquarium. Quelle solution peut-on envisager pour limiter ces pertes ?
Q 35. Estimer la puissance thermique perdue à travers l'ensemble des parois de l'aquarium. Quelle solution peut-on envisager pour limiter ces pertes ?
Données et formulaire
| Accélération de la pesanteur |
|
| Masse volumique de l'eau |
|
| Viscosité de l'eau |
|
| Masse volumique du verre |
|
| Conductivité thermique du verre |
|
| Capacité thermique massique du verre |
|
Couples oxydant-réducteur et potentiels standards À 298 K et pour
| Couple oxydant-réducteur | Valeur du potentiel standard |
|
|
|
|
|
|
|
|
|
|
|
|
Masses molaires
| Espèce chimique | Valeur de la masse molaire |
| Soude
|
|
| Chlorure de manganèse (II) |
|
| Dioxygène
|
|
| Iodure de potassium (KI) |
|
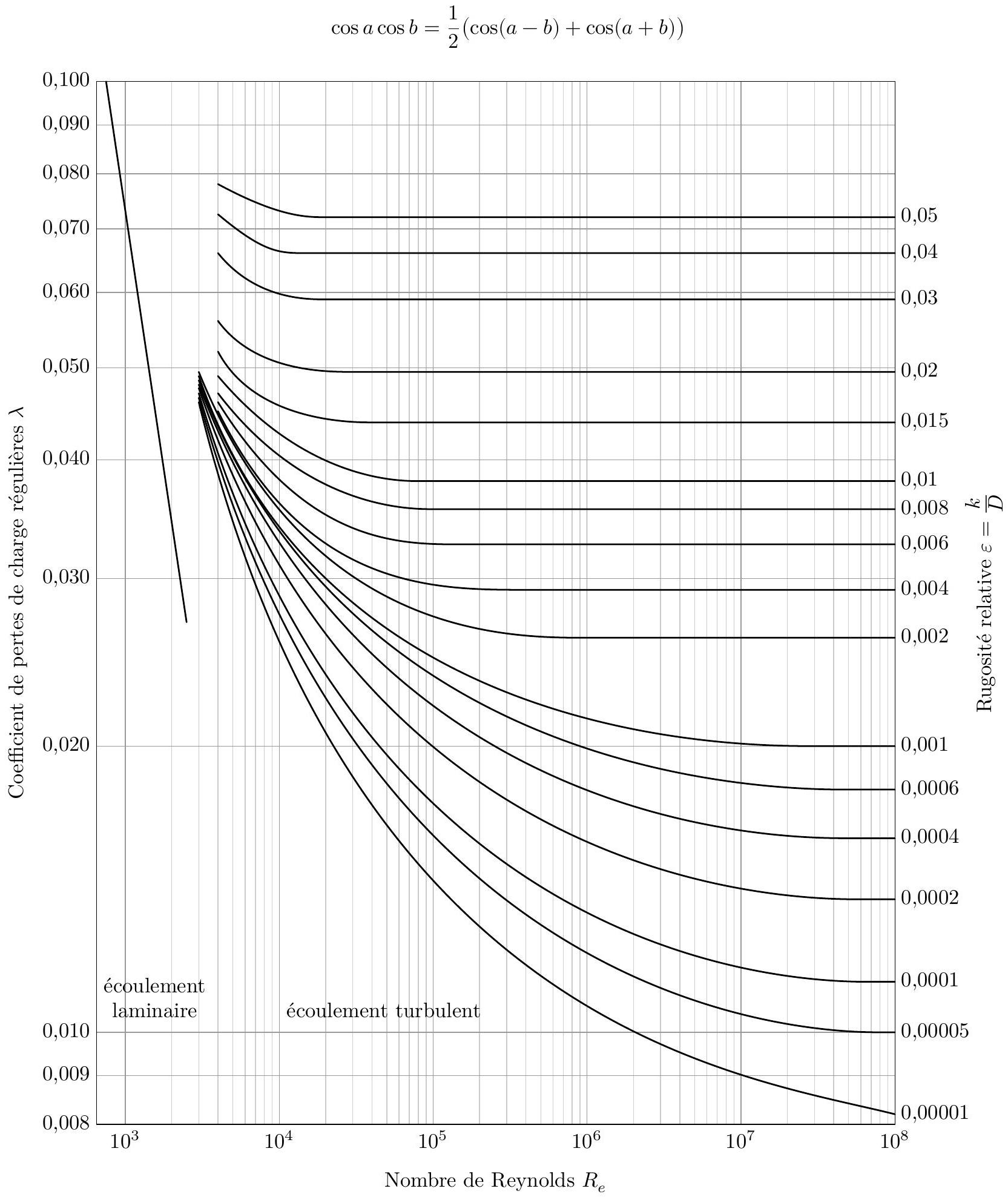
Figure 7 Diagramme de Moody

