Version interactive avec LaTeX compilé
Le projet Hyperloop
Le projet de transport commun terrestre Hyperloop
Ce projet étudie la possibilité de relier Los Angeles à San Francisco, villes californiennes distantes d'environ 600 km , en 35 minutes. Les passagers sont transportés dans des capsules, propulsées par un moteur à induction, qui se déplacent sur coussin d'air dans un tube à pression réduite. L'ensemble est alimenté par des cellules solaires disposées le long du tube. Les capsules sont équipées d'un compresseur utilisé pour produire le coussin d'air et une force de poussée additionnelle. L'alimentation électrique des éléments de la capsule est assurée par des batteries au lithium, rechargées à l'aide des cellules solaires.
Certaines données et formules sont données en fin de sujet.
Ce projet étudie la possibilité de relier Los Angeles à San Francisco, villes californiennes distantes d'environ 600 km , en 35 minutes. Les passagers sont transportés dans des capsules, propulsées par un moteur à induction, qui se déplacent sur coussin d'air dans un tube à pression réduite. L'ensemble est alimenté par des cellules solaires disposées le long du tube. Les capsules sont équipées d'un compresseur utilisé pour produire le coussin d'air et une force de poussée additionnelle. L'alimentation électrique des éléments de la capsule est assurée par des batteries au lithium, rechargées à l'aide des cellules solaires.
Certaines données et formules sont données en fin de sujet.
I L'air dans le tube
Le tube, de volume
I.A - Modélisation du fonctionnement d'une pompe à palette
Une pompe à palette simple étage est constituée
- d'un stator cylindrique creux muni d'un orifice d'aspiration et d'un orifice de refoulement équipé d'une soupape qui ne peut se soulever pour libérer l'air que si la pression sous celle-ci atteint la pression atmosphérique ;
- d'un rotor excentré par rapport au stator afin de modifier le volume offert au fluide lors de la phase de compression ;
- de deux palettes coulissantes installées dans le rotor, plaquées au stator par des ressorts (non représentés) et par la force centrifuge.
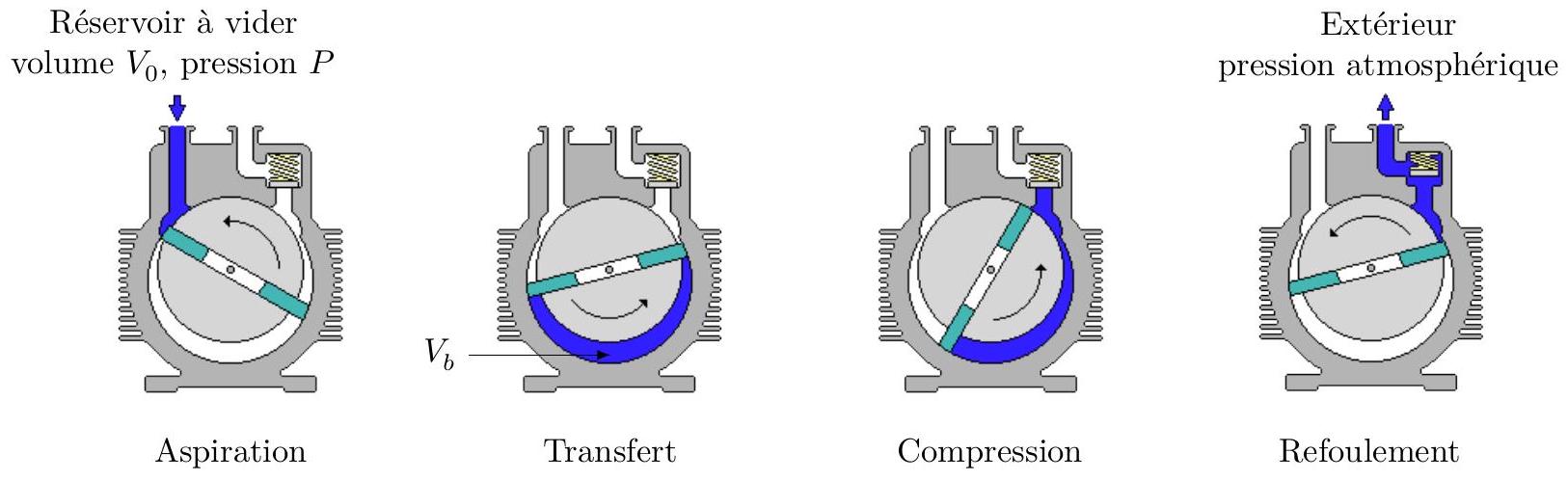
Figure 1 Cycle de fonctionnement d'une pompe à palette
L'air est aspiré dans la pompe, transféré, comprimé, puis refoulé. On note
I.A.1) Cette pompe est raccordée à un réservoir à vider, de volume
a) Déterminer la pression
I.A.1) Cette pompe est raccordée à un réservoir à vider, de volume
a) Déterminer la pression
b) De la même façon, déterminer la pression
c) Déterminer la pression minimale
d) Le débit volumique
I.A.2) La figure 2 présente la caractéristique (c'est-à-dire le débit volumique
c) Déterminer la pression minimale
d) Le débit volumique
I.A.2) La figure 2 présente la caractéristique (c'est-à-dire le débit volumique
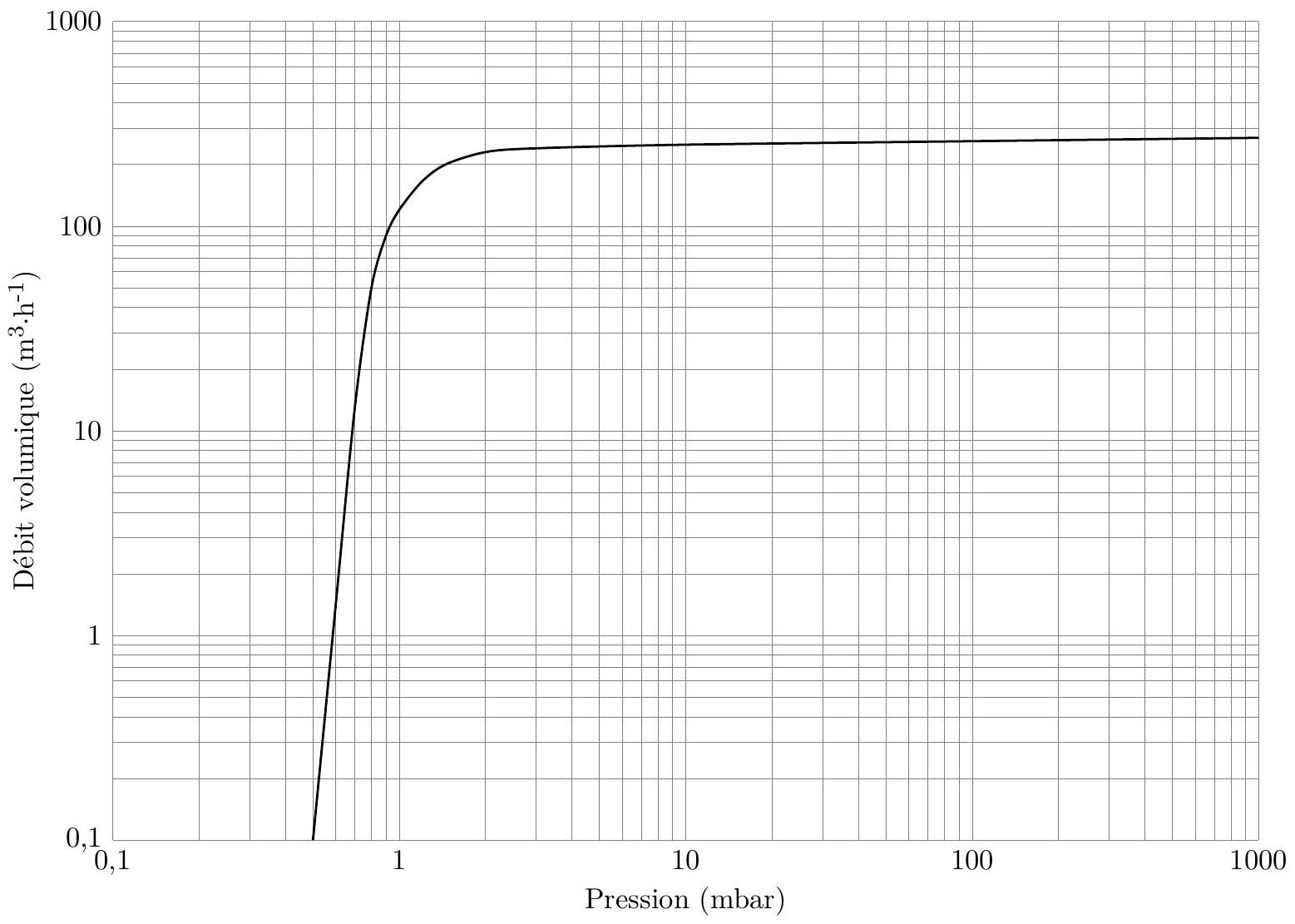
Figure 2 Caractéristique de la pompe Becker U
a) Pour quelles valeurs de la pression
b) On fait l'hypothèse qu'un volume d'air
c) Quelle est alors la pression minimale
d) Quels processus peuvent conduire à rajouter une certaine quantité d'air dans le réservoir à chaque cycle de pompage?
e) Est-ce que la modélisation du fonctionnement de la pompe à palette faite à la question b) permet de rendre compte correctement de la caractéristique présentée à la figure 2 ?
b) On fait l'hypothèse qu'un volume d'air
c) Quelle est alors la pression minimale
d) Quels processus peuvent conduire à rajouter une certaine quantité d'air dans le réservoir à chaque cycle de pompage?
e) Est-ce que la modélisation du fonctionnement de la pompe à palette faite à la question b) permet de rendre compte correctement de la caractéristique présentée à la figure 2 ?
I.B - Faire le vide
On installe
On souhaite évaluer le temps nécessaire pour atteindre une pression de 2 mbar dans le tube du projet Hyperloop, à partir de la pression atmosphérique.
I.B.1) Compte tenu de la pression à atteindre, justifier qu'on peut raisonnablement faire confiance à la modélisation effectuée à la question I.A.1. En déduire l'expression du débit volumique total
On souhaite évaluer le temps nécessaire pour atteindre une pression de 2 mbar dans le tube du projet Hyperloop, à partir de la pression atmosphérique.
I.B.1) Compte tenu de la pression à atteindre, justifier qu'on peut raisonnablement faire confiance à la modélisation effectuée à la question I.A.1. En déduire l'expression du débit volumique total
I.B.2) En utilisant le résultat de la question I.A. 1 et en considérant que
I.B.3) Déterminer les valeurs numériques du volume
I.B.3) Déterminer les valeurs numériques du volume
I.C - Déplacer l'air restant
Compte tenu de l'espace occupé par les capsules dans le tube et malgré la faible pression, à la vitesse de déplacement souhaitée, il se forme en avant de la capsule un coussin d'air produisant une force de pression importante. Il est donc prévu de disposer un compresseur à l'avant de la capsule afin de transporter l'air vers l'arrière. Ce dispositif réduit le frottement, apporte une force de poussée supplémentaire et permet de générer un coussin d'air pour assurer la sustentation de la capsule.
I.C.1)
a) Exprimer le premier principe de la thermodynamique pour un écoulement stationnaire. On prendra soin de définir les notations utilisées.
b) Compte tenu des conditions, on peut considérer que la compression est adiabatique, réversible, sans variation d'énergie cinétique ni d'énergie potentielle. Appliquer le premier principe au compresseur en tenant compte de ces conditions.
I.C.2) Dans le tube, l'air est à la température
I.C.3) Rappeler l'expression d'une variation d'enthalpie massique de l'air dans le tube en fonction d'une variation de la température.
b) Compte tenu des conditions, on peut considérer que la compression est adiabatique, réversible, sans variation d'énergie cinétique ni d'énergie potentielle. Appliquer le premier principe au compresseur en tenant compte de ces conditions.
I.C.2) Dans le tube, l'air est à la température
I.C.3) Rappeler l'expression d'une variation d'enthalpie massique de l'air dans le tube en fonction d'une variation de la température.
I.C.4)
a) Définir le débit massique
b) En considérant que la surface d'entrée du compresseur est de forme circulaire, de rayon
I.C.5) À l'aide de l'équation obtenue au I.C. 1 et en faisant intervenir le débit massique
I.C.6) Le document de présentation d'Hyperloop indique que le compresseur fournira une puissance mécanique de 328 kW à l'air. Déterminer littéralement puis numériquement la température
I.C.7) Déterminer la pression en sortie du compresseur
I.C.8) La valeur de la température obtenue à la question I.C. 6 est élevée. Pour cette raison, le projet prévoit de refroidir l'air à l'aide d'un échangeur à deux fluides. D'une part, l'air issu du compresseur, d'autre part de l'eau issue d'un réservoir embarqué. L'air se refroidit en circulant dans un tube autour duquel circule l'eau qui se réchauffe puis se vaporise. Après passage dans l'échangeur, l'eau est stockée dans un réservoir dans la capsule. On considère que l'échangeur est globalement calorifugé, c'est-à-dire que les seuls échanges thermiques qui se produisent se font entre les deux fluides. Il n'y a pas de partie mobile et les évolutions dans l'échangeur sont isobares. En entrée d'échangeur la température de l'eau est
a) Appliquer le premier principe de la thermodynamique pour un fluide en écoulement stationnaire à chacun des deux fluides entre son entrée et sa sortie de l'échangeur.
b) Donner les variations d'enthalpie massique de chacun des deux fluides en fonction de leurs capacités thermiques massiques, des températures d'entrée et sortie, de l'enthalpie de vaporisation de l'eau et de
c) En déduire les transferts thermiques massiques reçus par l'eau et par l'air dans l'échangeur en fonction des capacités thermiques massiques, des températures, de l'enthalpie de vaporisation de l'eau et de
I.C.9) Exprimer les puissances thermiques reçues par chaque fluide à sa traversée de l'échangeur.
I.C.10) L'échangeur étant calorifugé, quelle relation lie ces puissances ? En déduire la température de l'air en sortie de l'échangeur littéralement puis numériquement.
En réalité, pour des raisons pratiques, le projet prévoit une compression en deux étages, avec deux échangeurs.
b) En considérant que la surface d'entrée du compresseur est de forme circulaire, de rayon
I.C.5) À l'aide de l'équation obtenue au I.C. 1 et en faisant intervenir le débit massique
I.C.6) Le document de présentation d'Hyperloop indique que le compresseur fournira une puissance mécanique de 328 kW à l'air. Déterminer littéralement puis numériquement la température
I.C.7) Déterminer la pression en sortie du compresseur
I.C.8) La valeur de la température obtenue à la question I.C. 6 est élevée. Pour cette raison, le projet prévoit de refroidir l'air à l'aide d'un échangeur à deux fluides. D'une part, l'air issu du compresseur, d'autre part de l'eau issue d'un réservoir embarqué. L'air se refroidit en circulant dans un tube autour duquel circule l'eau qui se réchauffe puis se vaporise. Après passage dans l'échangeur, l'eau est stockée dans un réservoir dans la capsule. On considère que l'échangeur est globalement calorifugé, c'est-à-dire que les seuls échanges thermiques qui se produisent se font entre les deux fluides. Il n'y a pas de partie mobile et les évolutions dans l'échangeur sont isobares. En entrée d'échangeur la température de l'eau est
a) Appliquer le premier principe de la thermodynamique pour un fluide en écoulement stationnaire à chacun des deux fluides entre son entrée et sa sortie de l'échangeur.
b) Donner les variations d'enthalpie massique de chacun des deux fluides en fonction de leurs capacités thermiques massiques, des températures d'entrée et sortie, de l'enthalpie de vaporisation de l'eau et de
c) En déduire les transferts thermiques massiques reçus par l'eau et par l'air dans l'échangeur en fonction des capacités thermiques massiques, des températures, de l'enthalpie de vaporisation de l'eau et de
I.C.9) Exprimer les puissances thermiques reçues par chaque fluide à sa traversée de l'échangeur.
I.C.10) L'échangeur étant calorifugé, quelle relation lie ces puissances ? En déduire la température de l'air en sortie de l'échangeur littéralement puis numériquement.
En réalité, pour des raisons pratiques, le projet prévoit une compression en deux étages, avec deux échangeurs.
II L'alimentation électrique du compresseur
Pour alimenter le compresseur embarqué dans la capsule, le projet prévoit de recourir à des batteries rechargeables de type lithium-ion.
II.A - Le choix du lithium
L'isotope le plus abondant du lithium est le
II.A.1) Quelle est la composition d'un tel atome?
II.A.2) Donner sa configuration électronique dans l'état fondamental.
II.A.3) Où le lithium se situe-t-il dans la classification périodique des éléments ? À quelle famille appartient-il ?
II.A.4) Comment l'électronégativité des éléments évolue-t-elle si l'on se déplace dans la classification périodique de la gauche vers la droite ? Que peut-on en déduire concernant l'électronégativité du lithium ?
II.A.5) Justifier le caractère réducteur du lithium. Quel ion le lithium peut-il former ?
II.A.6) À température ambiante, le lithium possède une structure cubique centrée. Sa maille élémentaire est cubique, les atomes occupant les sommets du cube et le centre du cube. On caractérise cet arrangement par le côté du cube élémentaire, nommé paramètre de maille, noté
II.A.7) Le paramètre de maille vaut
II.A.8) Justifier l'intérêt de l'utilisation du lithium pour la constitution d'accumulateurs de forte énergie massique.
II.A.1) Quelle est la composition d'un tel atome?
II.A.2) Donner sa configuration électronique dans l'état fondamental.
II.A.3) Où le lithium se situe-t-il dans la classification périodique des éléments ? À quelle famille appartient-il ?
II.A.4) Comment l'électronégativité des éléments évolue-t-elle si l'on se déplace dans la classification périodique de la gauche vers la droite ? Que peut-on en déduire concernant l'électronégativité du lithium ?
II.A.5) Justifier le caractère réducteur du lithium. Quel ion le lithium peut-il former ?
II.A.6) À température ambiante, le lithium possède une structure cubique centrée. Sa maille élémentaire est cubique, les atomes occupant les sommets du cube et le centre du cube. On caractérise cet arrangement par le côté du cube élémentaire, nommé paramètre de maille, noté
II.A.7) Le paramètre de maille vaut
II.A.8) Justifier l'intérêt de l'utilisation du lithium pour la constitution d'accumulateurs de forte énergie massique.

Figure 3
II.B - Accumulateur Li-ion
Un accumulateur lithium-ion fonctionne par l'échange réversible d'ions lithium entre une électrode négative et une électrode positive.
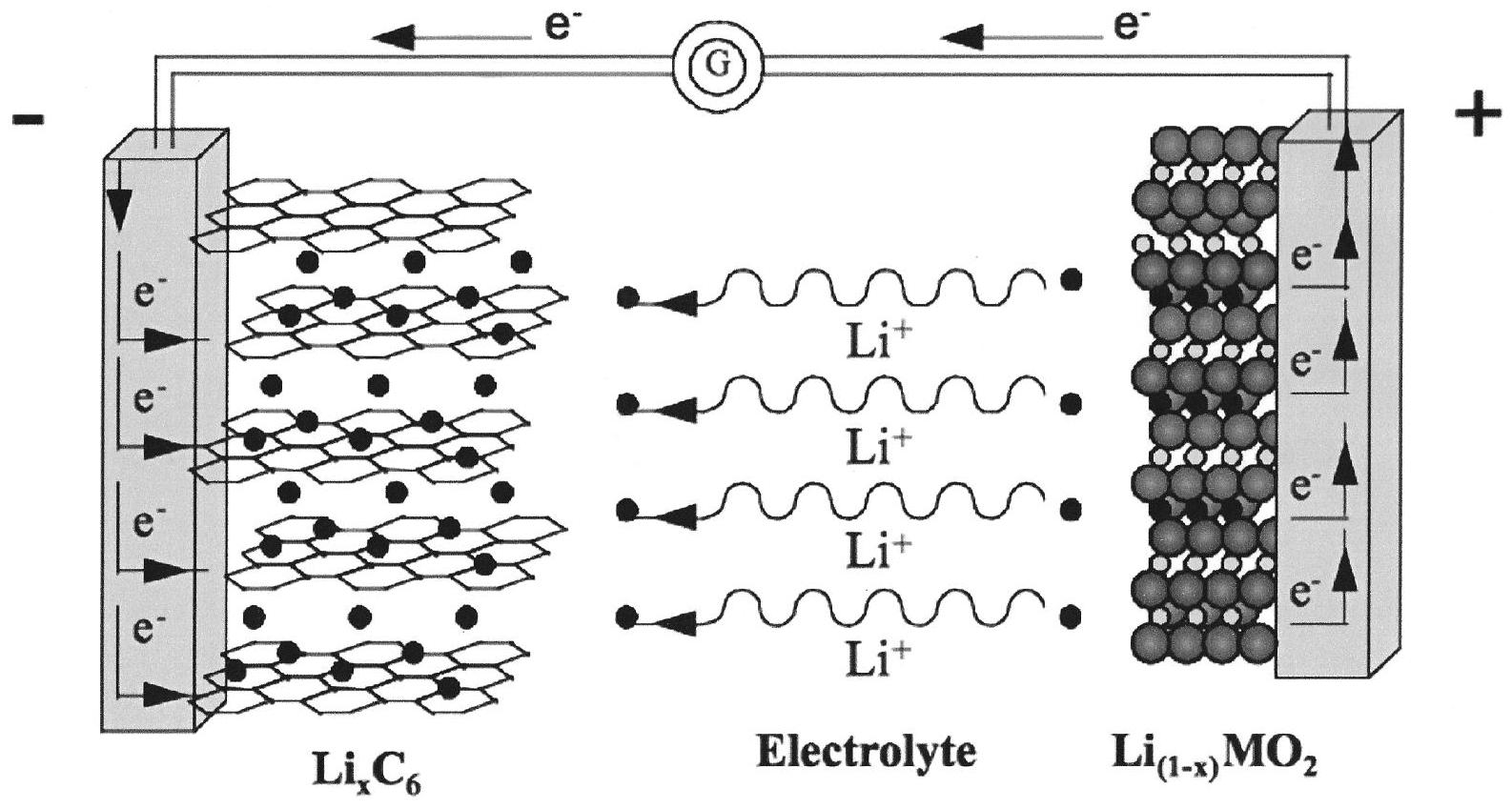
Figure 4 Schéma de fonctionnement du générateur lithium-ion représenté lors de sa charge
II.B.1) L'électrode négative
L'utilisation d'une électrode en lithium pour constituer l'électrode négative d'un accumulateur pose de nombreux problèmes, c'est la raison pour laquelle on a choisi d'utiliser le lithium en insertion dans une structure hôte. Les atomes de lithium sont insérés dans une structure carbonée, par exemple du graphite, on parle d'électrode au graphite lithié. Lors de la charge, la réaction électrochimique qui se produit est la réduction des ions lithium qui s'accompagne de l'insertion des atomes de lithium dans le graphite. Lors de la décharge, les atomes de lithium sont oxydés et les ions lithium se désinsèrent.
a) La formule chimique du composé d'insertion est
i. Rappeler la demi-équation de réduction des ions
ii. Écrire la réaction d'insertion des atomes de lithium dans le graphite.
iii. Les deux réactions se produisent simultanément, écrire la demi-équation bilan traduisant ces phénomènes pendant la charge.
a) La formule chimique du composé d'insertion est
i. Rappeler la demi-équation de réduction des ions
ii. Écrire la réaction d'insertion des atomes de lithium dans le graphite.
iii. Les deux réactions se produisent simultanément, écrire la demi-équation bilan traduisant ces phénomènes pendant la charge.
b) On souhaite déterminer la quantité maximale d'électricité que peut stocker cette électrode.
i. Déterminer le nombre maximum
ii. Lors de la décharge, chaque atome de lithium peut libérer un électron. Déterminer la charge électrique maximale
i. Déterminer le nombre maximum
ii. Lors de la décharge, chaque atome de lithium peut libérer un électron. Déterminer la charge électrique maximale
II.B.2) L'électrode positive
L'électrode positive est constituée d'un cristal d'oxyde de cobalt (
a) En considérant que le nombre d'oxydation de l'oxygène dans
b) Écrire la demi-équation qui se produit à cette électrode lors de la charge en tenant compte de l'insertion des ions lithium.
II.B.3) Écrire l'équation bilan du fonctionnement de l'accumulateur lors de la charge et lors de la décharge.
II.B.4) Le document de présentation de l'Hyperloop indique que la batterie lithium-ion utilisée devra fournir une puissance de 328 kW au compresseur pendant une durée de 45 minutes. La masse totale de cette batterie est de 1500 kg .
a) Déterminer l'énergie nécessaire au fonctionnement du compresseur pendant le trajet (en joule) puis convertir cette énergie en watt heure.
b) Déterminer la puissance massique que doit pouvoir fournir la batterie prévue, c'est-à-dire la puissance fournie par kg de batterie.
c) Déterminer l'énergie massique que doit pouvoir emmagasiner la batterie.
d) La figure 5 présente les puissances et énergies massiques accessibles en fonction des différentes technologies d'accumulateurs.
a) En considérant que le nombre d'oxydation de l'oxygène dans
b) Écrire la demi-équation qui se produit à cette électrode lors de la charge en tenant compte de l'insertion des ions lithium.
II.B.3) Écrire l'équation bilan du fonctionnement de l'accumulateur lors de la charge et lors de la décharge.
II.B.4) Le document de présentation de l'Hyperloop indique que la batterie lithium-ion utilisée devra fournir une puissance de 328 kW au compresseur pendant une durée de 45 minutes. La masse totale de cette batterie est de 1500 kg .
a) Déterminer l'énergie nécessaire au fonctionnement du compresseur pendant le trajet (en joule) puis convertir cette énergie en watt heure.
b) Déterminer la puissance massique que doit pouvoir fournir la batterie prévue, c'est-à-dire la puissance fournie par kg de batterie.
c) Déterminer l'énergie massique que doit pouvoir emmagasiner la batterie.
d) La figure 5 présente les puissances et énergies massiques accessibles en fonction des différentes technologies d'accumulateurs.
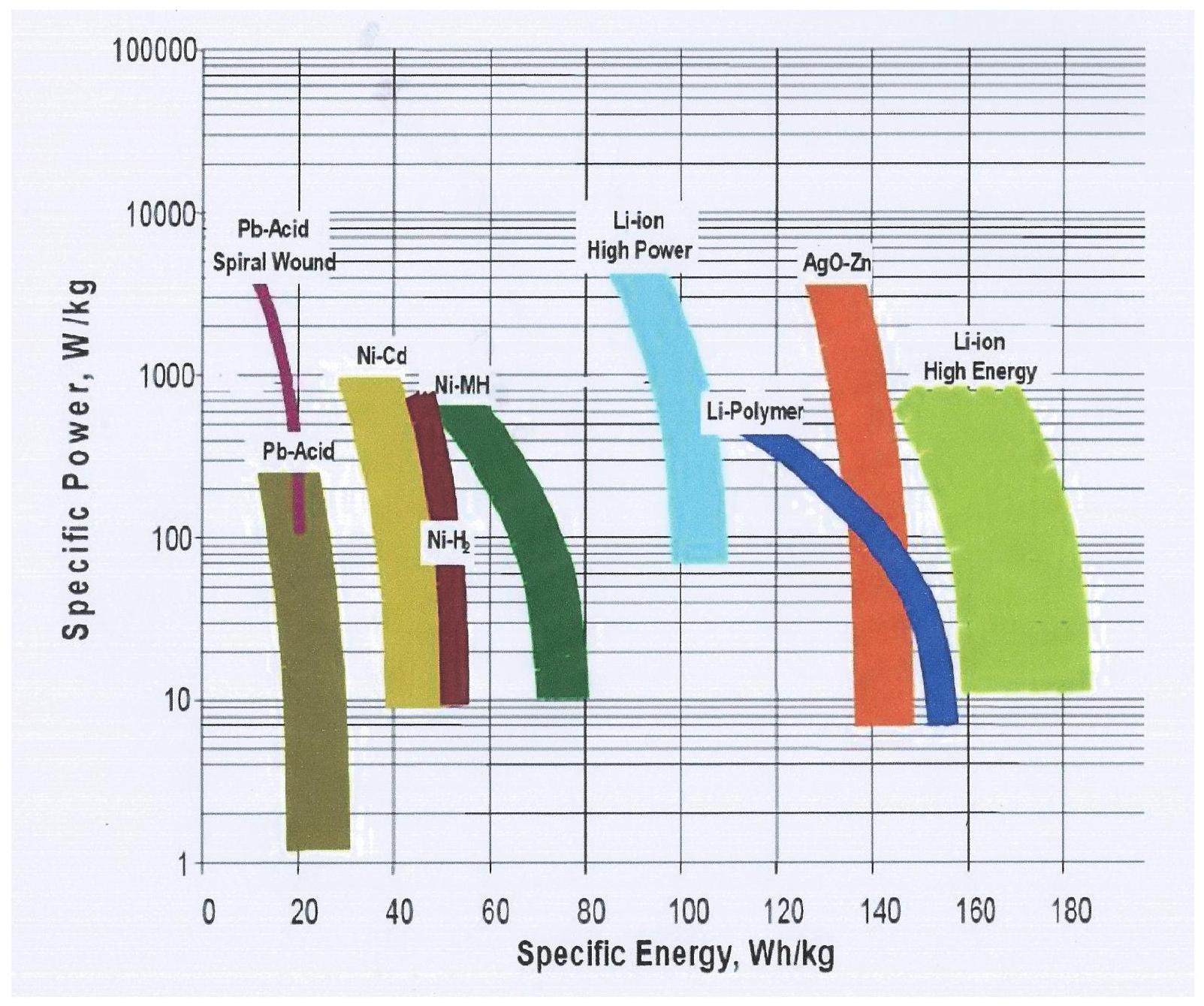
Figure 5 Puissance massique en fonction de l'énergie massique pour différentes technologies d'accumulateurs
Existe-t-il une technologie d'accumulateur compatible avec les indications données par le document de présentation. Si oui, laquelle?
II.C - Le choix de l'électrolyte
II.C.1)
a) Écrire la réaction entre le lithium et l'eau.
b) Justifier que cette réaction est très exothermique.
c) Justifier pourquoi on doit choisir un électrolyte non aqueux dans un accumulateur utilisant le lithium.
II.C.2) Dans les accumulateurs au lithium, on utilise des électrolytes organiques non aqueux. Un électrolyte couramment utilisé est constitué de sel de lithium
b) Justifier que cette réaction est très exothermique.
c) Justifier pourquoi on doit choisir un électrolyte non aqueux dans un accumulateur utilisant le lithium.
II.C.2) Dans les accumulateurs au lithium, on utilise des électrolytes organiques non aqueux. Un électrolyte couramment utilisé est constitué de sel de lithium
|
|
0 | 10 | 20 | 30 | 40 |
|
|
5 | 6,3 | 7,6 | 9,1 | 10,4 |
Tableau 1 Conductivité du LiPF 6
On souhaite comparer sa conductivité à celle d'un électrolyte aqueux couramment utilisé, le chlorure de potassium KCl à
Déterminer la conductivité du chlorure de potassium. La comparer à celle de l'électrolyte étudié à
Déterminer la conductivité du chlorure de potassium. La comparer à celle de l'électrolyte étudié à
III La propulsion de la capsule
Il est prévu d'assurer les accélérations et freinages de la capsule par un moteur linéaire à induction. Ce moteur est constitué d'un stator, fixe par rapport au tube et produisant un champ magnétique variable et d'une partie mobile, appelée «rotor», solidaire de la capsule (cf figure 7). Dans ce moteur, le «rotor» ne suit pas un mouvement de rotation, mais un mouvement de translation dans la direction du tube.
III.A - Production du champ magnétique
Le champ magnétique est produit par des paires de bobines disposées de part et d'autre du rotor. En première approximation, on peut considérer que ces bobines sont assimilables à des solénoïdes infinis.
III.A.1) On considère un solénoïde infini, d'axe
a) Énoncer le théorème d'Ampère.
b) Établir l'expression du champ magnétique crée à l'intérieur du solénoïde. On notera
III.A.2) Pour produire le champ statorique, on dispose régulièrement le long du tube des paires de solénoïdes en inversant le sens du courant à chaque changement de paires de solénoïdes. Ce dispositif permet de créer un champ magnétique dirigé selon
III.A.1) On considère un solénoïde infini, d'axe
a) Énoncer le théorème d'Ampère.
b) Établir l'expression du champ magnétique crée à l'intérieur du solénoïde. On notera
III.A.2) Pour produire le champ statorique, on dispose régulièrement le long du tube des paires de solénoïdes en inversant le sens du courant à chaque changement de paires de solénoïdes. Ce dispositif permet de créer un champ magnétique dirigé selon
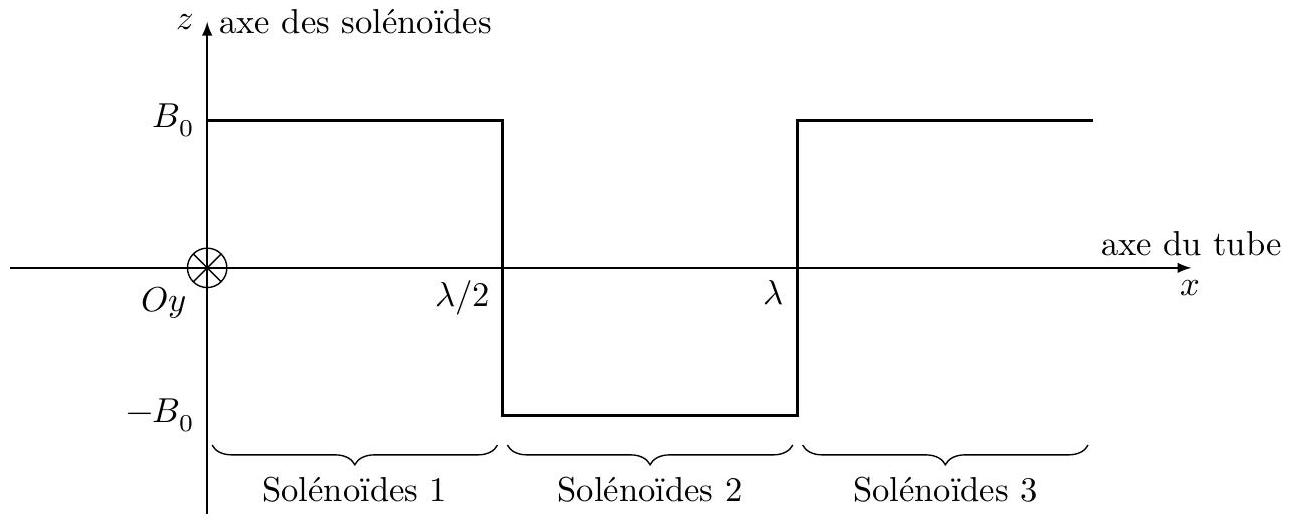
Figure 6
Le champ produit possédant une périodicité spatiale, il est possible de le décomposer en somme de fonctions sinusoïdales. En ne conservant que le premier terme de cette somme, on peut écrire
a) Exprimer
b) Montrer que
III.A.3) Pour le moteur étudié, on doit éliminer l'onde progressant selon
a) Exprimer
b) Montrer que
III.A.3) Pour le moteur étudié, on doit éliminer l'onde progressant selon
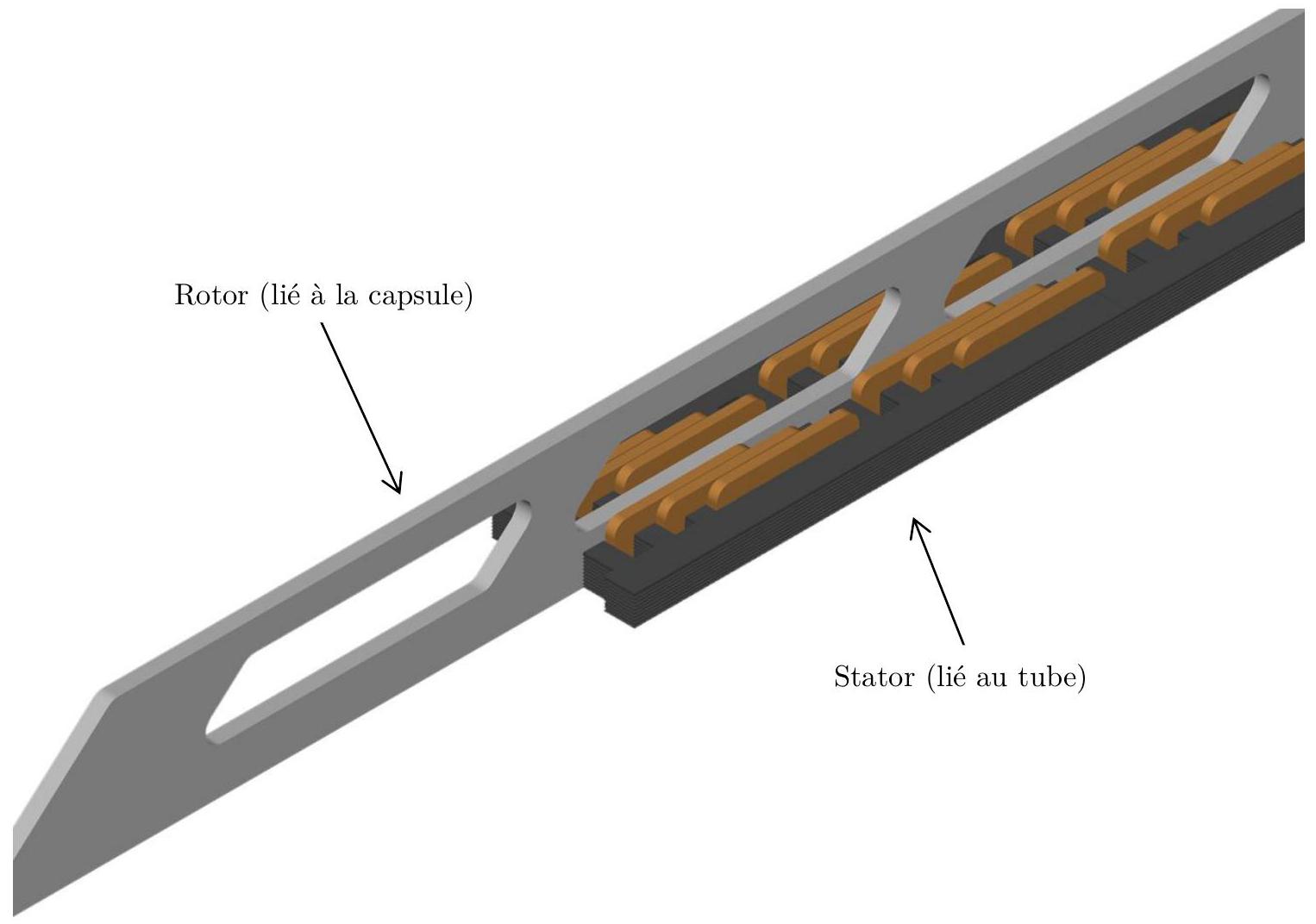
Figure 7 Moteur linéaire à induction
Le champ produit est alors la superposition des champs produits par les 3 paires et s'écrit
Montrer que le champ résultant peut s'écrire comme une onde progressive unique se propageant selon
III.B - Force s'exerçant sur le rotor
Le rotor, solidaire de la capsule, peut être modélisé par une spire filiforme carrée de côté
III.B.1) En considérant pour cette question que le champ magnétique créé par le stator est uniforme à l'échelle de la spire, de valeur sa valeur en
III.B.2) Déterminer la force électromotrice induite
III.B.3) Déterminer l'équation électrique décrivant l'évolution du courant induit circulant dans le rotor. En déduire l'expression du courant induit
III.B.4) En conservant l'expression de
III.B.1) En considérant pour cette question que le champ magnétique créé par le stator est uniforme à l'échelle de la spire, de valeur sa valeur en
III.B.2) Déterminer la force électromotrice induite
III.B.3) Déterminer l'équation électrique décrivant l'évolution du courant induit circulant dans le rotor. En déduire l'expression du courant induit
III.B.4) En conservant l'expression de
III.B.5) La capsule peut-elle démarrer par l'action de cette seule force ?
III.B.6) Que faut-il faire si l'on souhaite freiner la capsule à l'aide de ce système ?
III.B.6) Que faut-il faire si l'on souhaite freiner la capsule à l'aide de ce système ?
Données et formulaire
Conversion
Constante des gaz parfaits
Constante d'Avogadro
Charge électrique d'un électron
Pression atmosphérique
Masse molaire de l'air
Capacité thermique massique à pression constante de l'air
Coefficient
Capacité thermique massique de l'eau liquide
Enthalpie massique de vaporisation de l'eau
Capacité thermique massique de la vapeur d'eau
Capacité thermique massique à pression constante du dihydrogène
Masse molaire du dihydrogène
Masse molaire du lithium
Masse molaire du carbone
Masse molaire de l'oxygène
Conductivités molaires à
Constante d'Avogadro
Charge électrique d'un électron
Pression atmosphérique
Masse molaire de l'air
Capacité thermique massique à pression constante de l'air
Coefficient
Capacité thermique massique de l'eau liquide
Enthalpie massique de vaporisation de l'eau
Capacité thermique massique de la vapeur d'eau
Capacité thermique massique à pression constante du dihydrogène
Masse molaire du dihydrogène
Masse molaire du lithium
Masse molaire du carbone
Masse molaire de l'oxygène
Conductivités molaires à
1 bar
Données thermodynamiques à 298 K
|
|||
|
|
0 | ||
|
|
0 | ||
|
|
-285 | ||
|
|
-508 |
Trigonométrie
d'après Audrey Martinent, 2001 (http://electrochimie.minatec.grenoble-inp.fr/THESEAMartinent.pdf) d'après NASA/TM 2003212730 (http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20040010319.pdf)
