Version interactive avec LaTeX compilé
Option informatique
Arbres couvrants et pavages
Le seul langage de programmation autorisé dans cette épreuve est Caml.
Toutes les fonctions des modules Array et List, ainsi que les fonctions de la bibliothèque standard (celles qui s'écrivent sans nom de module, comme max ou incr ainsi que les opérateurs comme / ou mod) peuvent être librement utilisés.
On utilisera également le générateur pseudo-aléatoire int du module Random. Quand n est un entier supérieur ou égal à 1, l'appel Random. int n renvoie un entier dans l'intervalle
Les candidats ne devront faire appel à aucun autre module.
En Caml, les tableaux d'objets d'un certain type 'a sont représentés par le type 'a array. L'expression tab. (i) permet d'accéder à l'élément situé en i-ème position du tableau tab. Dans le texte, en dehors du code Caml, cet élément sera noté
Toutes les fonctions des modules Array et List, ainsi que les fonctions de la bibliothèque standard (celles qui s'écrivent sans nom de module, comme max ou incr ainsi que les opérateurs comme / ou mod) peuvent être librement utilisés.
On utilisera également le générateur pseudo-aléatoire int du module Random. Quand n est un entier supérieur ou égal à 1, l'appel Random. int n renvoie un entier dans l'intervalle
Les candidats ne devront faire appel à aucun autre module.
En Caml, les tableaux d'objets d'un certain type 'a sont représentés par le type 'a array. L'expression tab. (i) permet d'accéder à l'élément situé en i-ème position du tableau tab. Dans le texte, en dehors du code Caml, cet élément sera noté
Dans ce problème, un graphe
-
est un ensemble fini dont les éléments sont les sommets de ; -
est la suite des arêtes de , une arête étant une partie de de cardinal 2 . Les sommets et sont appelés les extrémités de l'arête et on dira que a relie et . Si et sont reliés par une arête, on dit qu'ils sont voisins ou adjacents.
Ainsi, les graphes sont non orientés et il n'y a pas d'arête reliant un sommet à lui-même. Par contre, à partir de la partie V, il est possible que plusieurs arêtes aient les mêmes extrémités.
Par convention, nous noterons(respectivement ) le nombre de sommets (respectivement d'arêtes) du graphe et nous supposerons que .
Un graphe sera représenté par le type
type graphe = int list array
Siest un graphe représenté par , alors le nombre de sommets du graphe est donné par la longueur du tableau g. De plus, si , alors g. (s) est une liste contenant les indices des sommets voisins de , dans un ordre quelconque, chaque sommet apparaissant autant de fois qu'il existe d'arêtes vers .
Les complexités temporelles demandées sont des complexités dans le pire des cas et seront exprimées sous la forme
Nous utiliserons la représentation graphique habituelle des graphes. Le graphe
let
peut être représenté par le graphique de la figure 1.
let
peut être représenté par le graphique de la figure 1.
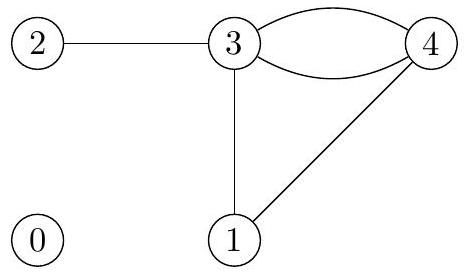
Figure 1 Exemple de graphe
Pour
Par ailleurs, l'ordre des arêtes ayant une importance en partie V , on convient de numéroter les
Par ailleurs, l'ordre des arêtes ayant une importance en partie V , on convient de numéroter les

Figure 2 Le graphe
Soit
- Si
, le tableau d'adjacence de est le tableau, dans un ordre quelconque, des voisins de , chaque sommet apparaissant autant de fois qu'il existe d'arêtes vers . On note le tableau de taille tel que, pour tout est le tableau d'adjacence du sommet . Adj est donc représenté par une variable adj de type int array array. - Un chemin dans
est une suite où pour tout compris entre 1 et et sont des sommets voisins. On dira que est un chemin de à de longueur . Par convention, pour sommet de , il existe un chemin de longueur nulle de à . - La composante connexe d'un sommet
de , notée , est l'ensemble des sommets de tels qu'il existe un chemin de à . - On dit que
est connexe si pour tous sommets et de , il existe un chemin de à . - Un cycle dans
est un chemin de longueur d'un sommet à lui-même et dont les arêtes sont deux à deux distinctes. On dit que est acyclique s'il ne contient aucun cycle. - Un arbre est un graphe connexe acyclique.
I Quelques fonctions auxiliaires
Q 1. Écrire une fonction
nombre_aretes : graphe -> int
qui, appliquée à g représentant un graphe
Q 2. Écrire une commande Caml permettant de créer le tableau des tableaux d'adjacence Adj associé au graphe
On rappelle que la fonction Array.of_list : 'a list
Q 3. Écrire une fonction
adjacence : graphe -> int array array
qui, appliquée à g représentant un graphe
Q 4. Écrire une fonction
rang : int * int -> int * int -> int
telle que rang (p,q) (s, t) renvoie le rang de l'arête
Q 5. Écrire de même sa fonction réciproque
sommets : int * int -> int -> int * int
telle que sommets (
Q 6. Écrire une fonction
quadrillage : int -> int -> graphe
telle que l'instruction quadrillage p q renvoie le graphe représentant
nombre_aretes : graphe -> int
qui, appliquée à g représentant un graphe
Q 2. Écrire une commande Caml permettant de créer le tableau des tableaux d'adjacence Adj associé au graphe
On rappelle que la fonction Array.of_list : 'a list
Q 3. Écrire une fonction
adjacence : graphe -> int array array
qui, appliquée à g représentant un graphe
Q 4. Écrire une fonction
rang : int * int -> int * int -> int
telle que rang (p,q) (s, t) renvoie le rang de l'arête
Q 5. Écrire de même sa fonction réciproque
sommets : int * int -> int -> int * int
telle que sommets (
Q 6. Écrire une fonction
quadrillage : int -> int -> graphe
telle que l'instruction quadrillage p q renvoie le graphe représentant
II Caractérisation des arbres
Soit
II.A - Propriétés sur les arbres
Q 7. Montrer que les composantes connexes de
-
; - pour tous sommets
et , soit , soit .
Q 8. Montrer que si
Pour
Q 9. On suppose que
Q 10. Montrer que les trois propriétés suivantes sont équivalentes:
(i)
(ii)
(iii)
Pour
Q 9. On suppose que
Q 10. Montrer que les trois propriétés suivantes sont équivalentes:
(i)
(ii)
(iii)
II.B - Manipulation de partitions
Nous souhaitons écrire une fonction qui teste si un graphe est un arbre. Nous allons pour cela utiliser une structure de données permettant de manipuler les partitions de l'ensemble
- de calculer, pour
, le représentant de la partie contenant ; cet élément sera également appelé représentant de ; - pour deux entiers
et représentant des parties distinctes et , de transformer en réunissant et ou devenant le représentant de la partie .
Nous représenterons une partitionde par une forêt: chaque est représenté par un arbre dont les noeuds sont étiquetés par les éléments de et de racine le représentant de , les arcs étant orientés vers la racine. Nous noterons la hauteur de l'arbre , c'est-à-dire la longueur de sa plus longue branche. Ainsi, est une partition de et peut par exemple être représentée par la forêt de la figure 3.

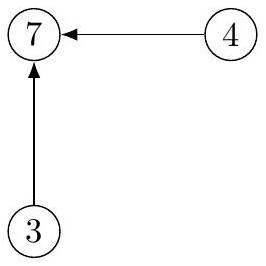
Figure 3 Une représentation de
Le calcul du représentant d'un entier
Une partition
[I -2; 5; 0; 7; 7; 6; -3; -2; 6 I]
Une partition
[I -2; 5; 0; 7; 7; 6; -3; -2; 6 I]
La réunion de deux parties
- si
est choisi pour représentant de la partie et devient le père de ; - si
est choisi pour représentant de la partie et devient le père de .
Par exemple, la réunion des parties
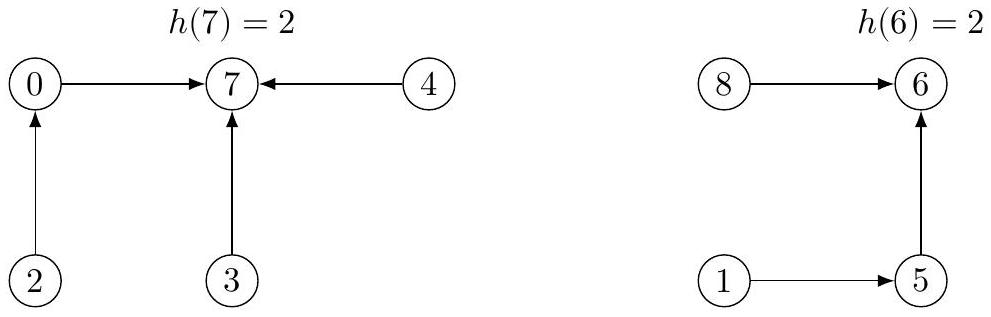
Figure 4 Une représentation de
Q 11. Écrire une fonction
representant : int array -> int -> int
qui, appliquée à un tableau représentant une partition de
Q 12. Écrire une fonction
Q 12. Écrire une fonction
union : int array -> int -> int -> unit
qui, appliquée à un tableau représentant une partition de
On note
Q 13. Soit
Q 14. En déduire les complexités des deux fonctions précédentes dans le pire des cas en fonction de
Q 15. Écrire une fonction
est_un_arbre : graphe -> bool
qui, appliquée à un graphe g représentant un graphe
On note
Q 13. Soit
Q 14. En déduire les complexités des deux fonctions précédentes dans le pire des cas en fonction de
Q 15. Écrire une fonction
est_un_arbre : graphe -> bool
qui, appliquée à un graphe g représentant un graphe
III Algorithme de Wilson : arbre couvrant aléatoire
Si
La figure 5 représente deux arbres couvrants du graphe
La figure 5 représente deux arbres couvrants du graphe

Figure 5 Deux arbres couvrants enracinés de
Dans cette partie, nous supposons que
Nous allons pour cela faire évoluer dynamiquement un arbre
Nous allons pour cela faire évoluer dynamiquement un arbre
- parent. (r) = -1;
- si
n'est pas un sommet de , parent. (s) = -2; - si
est un sommet de autre que la racine, parent. (s) est le père de dans l'arbre .
Nous partons de l'arbre réduit à la racine
- au début du calcul,
est réduit à ; - à tout moment,
est de la forme ( ) où les sommets sont deux à deux distincts et les sommets ne sont pas des sommets de ; - tant que l'extrémité
n'est pas un sommet de , on choisit aléatoirement et uniformément un voisin de et on distingue, - si
, on supprime le cycle qui vient d'être formé et devient le nouveau point d'arrivée du chemin ; - sinon,
devient le chemin ; - on renvoie le chemin (
) une fois le calcul terminé.
On représentera un chemin en Caml par le type :
type chemin
de telle sorte que si le chemin
type chemin
de telle sorte que si le chemin
On rappelle que si c est un objet de type chemin et u un entier représentant un sommet, la modification du champ mutable c.fin pour y mettre u peut se faire avec la commande:
c.fin <- u
c.fin <- u
Q 16. Déterminer, dans le graphe
{debut = 1; fin = 4; suivant = [|-5; 2; 5; 3; -1; 4|]}
Q 17. Que peut-on dire de la terminaison de cet algorithme?
Q 18. Écrire une fonction
marche_aleatoire : int array array -> int array -> int -> chemin
telle que l'appel marche_aleatoire adj parent s renvoie l'objet c représentant un chemin de
{debut = 1; fin = 4; suivant = [|-5; 2; 5; 3; -1; 4|]}
Q 17. Que peut-on dire de la terminaison de cet algorithme?
Q 18. Écrire une fonction
marche_aleatoire : int array array -> int array -> int -> chemin
telle que l'appel marche_aleatoire adj parent s renvoie l'objet c représentant un chemin de
L'algorithme d'évolution de
Q 19. Écrire une fonction
greffe : int array -> chemin -> unit
telle que l'instruction greffe parent c modifie parent de sorte à représenter l'arbre obtenu après la greffe du chemin
Q 20. Écrire une fonction
wilson : graphe -> int -> int array
tel que wilson gr renvoie un arbre couvrant aléatoire du graphe
Q 19. Écrire une fonction
greffe : int array -> chemin -> unit
telle que l'instruction greffe parent c modifie parent de sorte à représenter l'arbre obtenu après la greffe du chemin
Q 20. Écrire une fonction
wilson : graphe -> int -> int array
tel que wilson gr renvoie un arbre couvrant aléatoire du graphe
IV Arbres couvrants et pavages par des dominos
Soient
Les cases dont les deux coordonnées sont paires sont colorées en noir, celles dont les deux coordonnées sont impaires sont colorées en gris, les autres sont colorées en blanc.
Si
Les cases dont les deux coordonnées sont paires sont colorées en noir, celles dont les deux coordonnées sont impaires sont colorées en gris, les autres sont colorées en blanc.
Si

Figure 6 L'échiquier
Nous définissons le type
type direction
et nous codons
type direction
et nous codons
- si
et ont la même parité et si , p. (i). (j) est la direction du domino qui recouvre la case (cette case est soit noire, soit grise) ; - sinon, pavage. (i). (j) prend la valeur
(ces valeurs ne jouent aucun rôle).
Ainsi, si p1 est la matrice associée au pavage
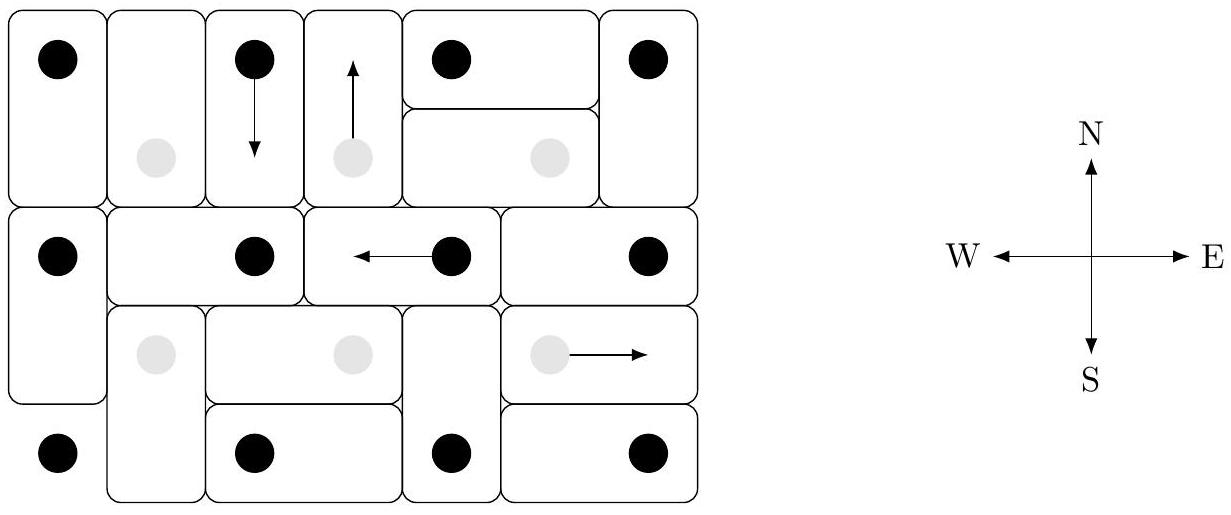
Figure 7 Le pavage
Les cases noires de l'échiquier
Pour toute la suite du sujet, les valeurs de
let
Pour toute la suite du sujet, les valeurs de
let
IV.A - Exemples
Q 21. Dessiner l'arbre couvrant non enraciné
Q 22. Considérons inversement l'arbre couvrant
Q 22. Considérons inversement l'arbre couvrant
IV.B - Calcul de l'arbre couvrant associé à un pavage
Q 23. Soit

Figure 8 L'arbre couvant
Q 24. Écrire une fonction
coord_noire : int -> int * int
telle que l'instruction coord_noire s renvoie le couple des coordonnées de la case correspondant au sommet
Q 25. Écrire une fonction
Q 25. Écrire une fonction
sommet_direction : int -> direction -> int
telle que sommet_direction
Q 26. Écrire une fonction
Q 26. Écrire une fonction
phi : direction array array -> int array
qui, appliquée à une matrice pavage représentant un pavage
V Utilisation du dual pour la construction d'un pavage
Le graphe
Ainsi, le sommet 6 de
Dans la suite du problème, nous notons :
Ainsi, le sommet 6 de
Dans la suite du problème, nous notons :
-
le nombre de sommets de ;
le nombre de sommets de ; -
le nombre d'arêtes de et de ; -
l'ensemble des arêtes de ; -
l'ensemble des arêtes de .
Nous supposerons définies pour la suite :
- une fonction coord_grise : int -> int * int qui, appliquée à un sommet de
autre que 0 , renvoie les coordonnées de la case grise qui correspond à ce sommet ; - une fonction numero : int * int -> int qui, appliquée à un couple (
) représentant une case noire ou grise de l'échiquier , renvoie le sommet du graphe ou associé à cette case. On supposera également que dans tous les autres cas, numero renvoie la valeur 0 , y compris si les coordonnées sont en dehors de l'échiquier. Quand et , nous avons par exemple : numero , numero , et numero .
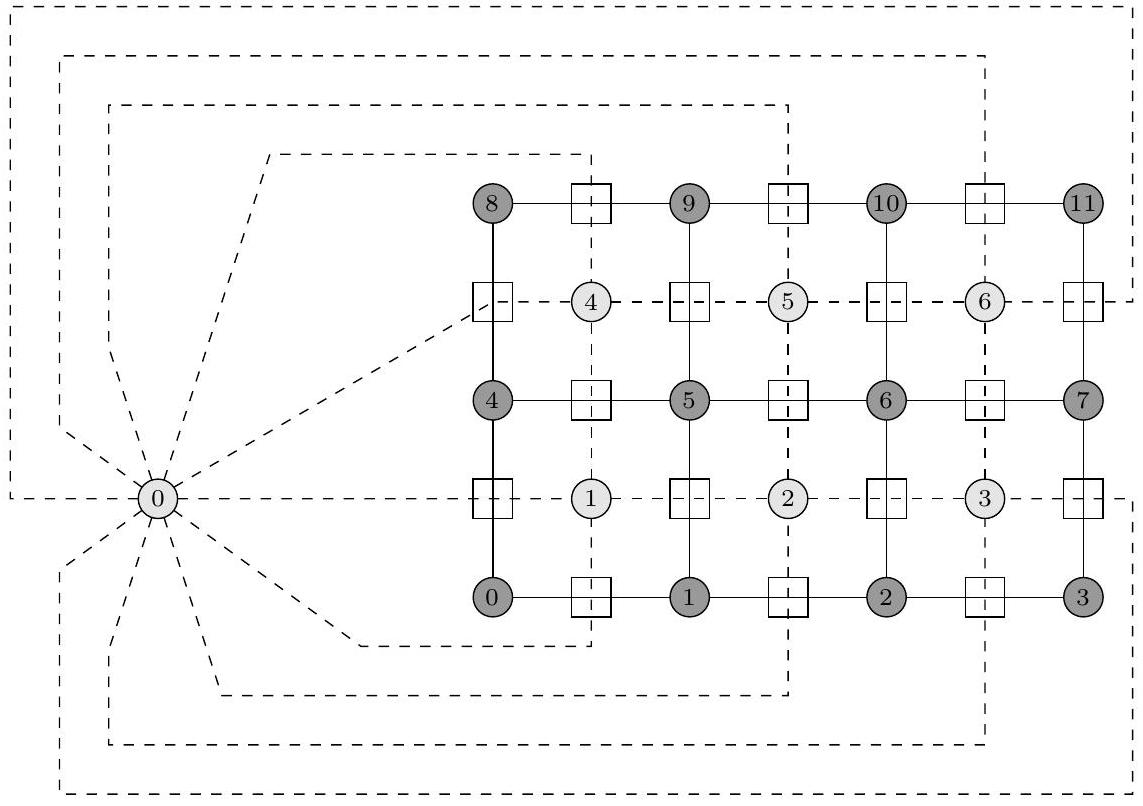
Figure
Q 27. En utilisant les fonctions précédentes, écrire une fonction
dual : unit -> graphe
telle que l'instruction dual () renvoie le graphe représentant
On suppose désormais définie une variable globale g_etoile par l'instruction
let g_etoile = dual () ;;
V.B - Dual d'un arbre couvrant
dual : unit -> graphe
telle que l'instruction dual () renvoie le graphe représentant
On suppose désormais définie une variable globale g_etoile par l'instruction
let g_etoile = dual () ;;
V.B - Dual d'un arbre couvrant
Q 28. Montrer que, quitte à renuméroter les sommets, le dual de
Soit
Soit
Q 29. Montrer que si le graphe (
Q 30. En déduire que (
Si
Pour construire l'arbre
La figure 10 représente les deux arbres couvrants du graphe
Q 30. En déduire que (
Si
Pour construire l'arbre
La figure 10 représente les deux arbres couvrants du graphe

Figure 10 Deux arbres couvrants enracinés de
Q 31. Écrire une fonction
vers_couple : int array -> int * bool array
telle que l'instruction vers_couple parent, où parent est un tableau représentant un arbre enraciné de
vers_couple : int array -> int * bool array
telle que l'instruction vers_couple parent, où parent est un tableau représentant un arbre enraciné de
Q 32. Détailler en français un algorithme permettant de construire parent à partir du couple (
Q 33. Écrire une fonction
vers_parent : int * bool array -> int array
telle que l'instruction vers_parent (
Q 34. Déterminer les complexités de ces deux fonctions de conversion en fonction de
On supposera écrite une fonction vers_parent_etoile : int * bool array -> int array, ayant un fonctionnement similaire à vers_parent, qui prend en argument un couple (r, b_etoile) correspondant à un arbre couvrant
Q 35. Écrire une fonction
arbre_dual : int array -> int array
qui, appliquée au tableau parent représentant un arbre couvrant
V.C - Calcul du pavage associé à un arbre couvrant
Q 33. Écrire une fonction
vers_parent : int * bool array -> int array
telle que l'instruction vers_parent (
Q 34. Déterminer les complexités de ces deux fonctions de conversion en fonction de
On supposera écrite une fonction vers_parent_etoile : int * bool array -> int array, ayant un fonctionnement similaire à vers_parent, qui prend en argument un couple (r, b_etoile) correspondant à un arbre couvrant
Q 35. Écrire une fonction
arbre_dual : int array -> int array
qui, appliquée au tableau parent représentant un arbre couvrant
V.C - Calcul du pavage associé à un arbre couvrant
Soit
Q 36. Décrire un procédé de construction, à partir des arbres
Q 37. Écrire une fonction
pavage_aleatoire : unit -> direction array array
telle que l'instruction pavage_aleatoire () renvoie une matrice de taille (
Q 38. Comment adapter cette méthode à la construction de pavages aléatoires d'un échiquier à
Q 36. Décrire un procédé de construction, à partir des arbres
Q 37. Écrire une fonction
pavage_aleatoire : unit -> direction array array
telle que l'instruction pavage_aleatoire () renvoie une matrice de taille (
Q 38. Comment adapter cette méthode à la construction de pavages aléatoires d'un échiquier à
