Centrale Option Informatique MP 2018

Étude du jeu Ricochet Robots

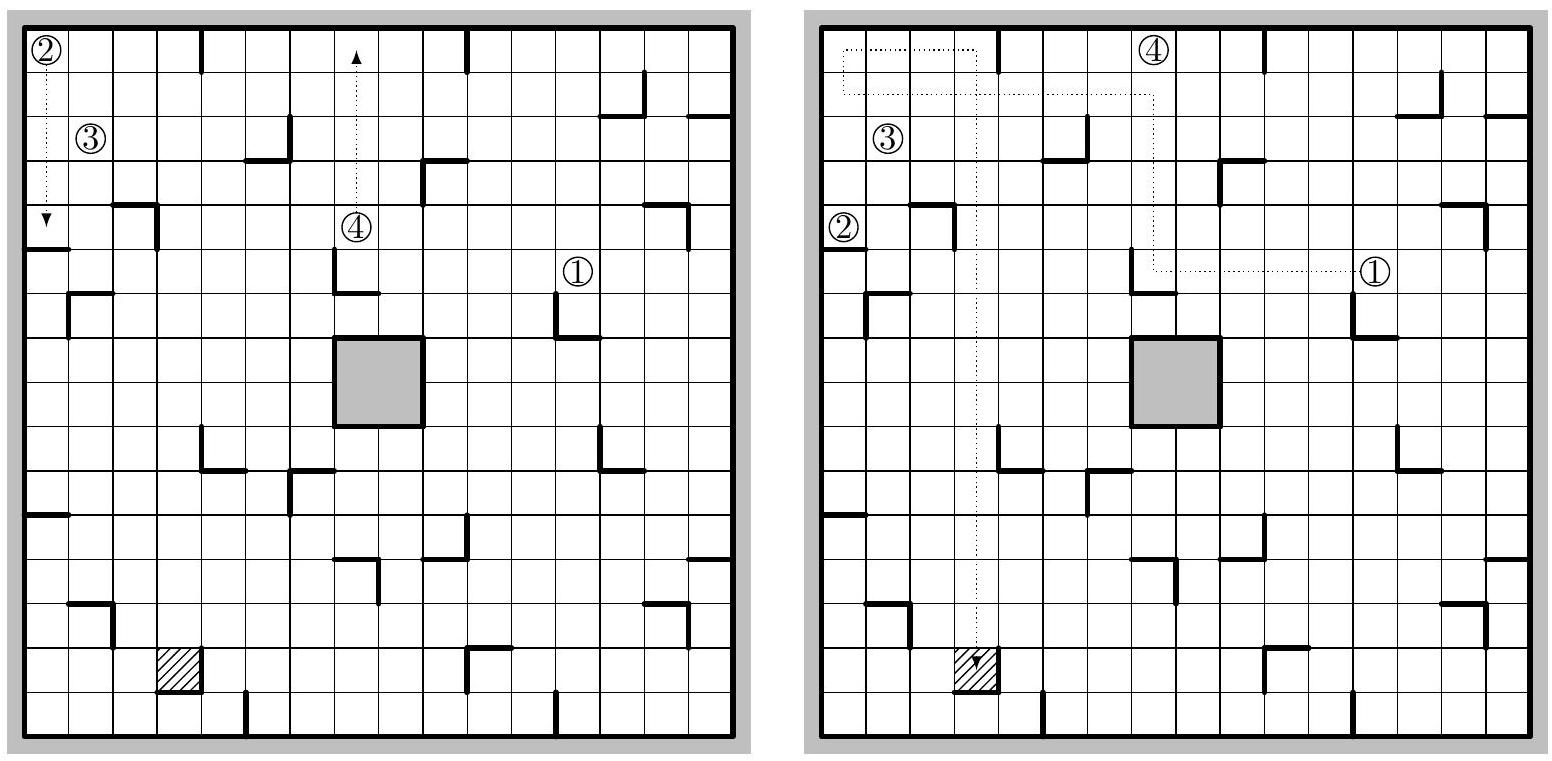
Figure 1 Le jeu des robots : le but est d'amener le robot 1 sur la case hachurée. À gauche : deux déplacements des robots 2 et 4 ; à droite : six déplacements du robot 1 . Le jeu est résolu en 8 mouvements (solution optimale)

• copy_vect : 'a vect -> 'a vect telle que l'appel copy_vect v renvoie un nouveau tableau contenant les valeurs contenues dans v;
• make_vect : int -> 'a -> 'a vect telle que l'appel make_vect renvoie un nouveau tableau de longueur n initialisé avec des éléments égaux à x ;
• make_matrix : int -> int -> 'a -> 'a vect vect telle que l'appel make_matrix p q x renvoie une nouvelle matrice à p lignes et q colonnes initialisée avec des éléments égaux à x.

I Déplacement d'un robot dans une grille

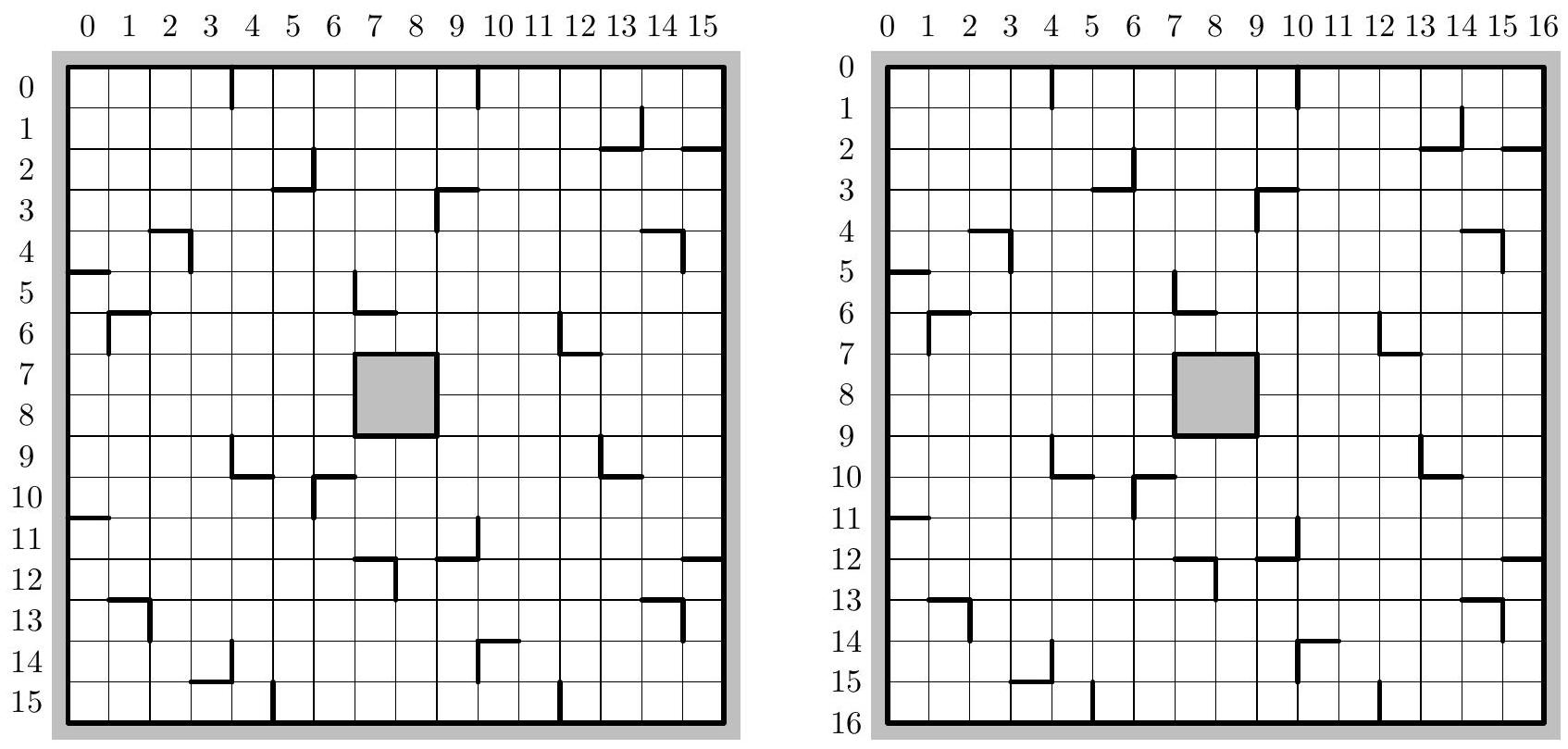
Figure 2 À gauche : numérotation des cases par ligne/colonne ; à droite : numérotation des lignes horizontales et verticales

let obstacles_lignes = [| [|0; 4; 10; 16|]; [|0; 14; 16|]; [|0; 6; 16|];
    [|0; 9; 16|]; [|0; 3; 15; 16|]; [|0; 7; 16|]; [|0; 1; 12; 16|]; [|0; 7; 9; 16|];
    [|0; 7; 9; 16|]; [|0; 4; 13; 16|]; [|0; 6; 16|]; [|0; 10; 16|]; [|0; 8; 16|];
    [|0; 2; 15; 16|]; [|0; 4; 10; 16|]; [|0; 5; 12; 16|] |];;
let obstacles_colonnes = [| [|0; 5; 11; 16|]; [|0; 6; 13; 16|]; [|0; 4; 16|];
    [|0; 15; 16|]; [|0; 10; 16|]; [|0; 3; 16|]; [|0; 10; 16|]; [|0; 6; 7; 9; 12; 16|];
    [|0; 7; 9; 16|]; [|0; 3; 12; 16|]; [|0; 14; 16|]; [|0; 16|]; [|0; 7; 16|];
    [|0; 2; 10; 16|]; [|0; 4; 13; 16|]; [|0; 2; 12; 16|] |];;

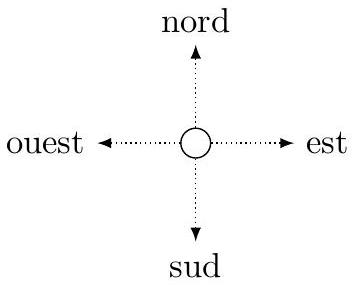
Figure 4 Déplacements cardinaux

(int * int) vect -> int * int -> int * int -> unit

int * int -> (int * int) list -> (int * int) vect

II Quelques fonctions utilitaires

II.A - Une fonction de tri

II.B - Quelques fonctions sur les listes

II.C - Implantation d'une structure de file

type 'a file = {mutable entree: 'a list; mutable sortie: 'a list};;

III Tables de hachage

• recherche d'un élément connaissant sa clé ;
• ajout d'un couple (clé, élément) ;
• suppression d'un couple connaissant sa clé.

III.A - Une famille de fonctions

III.B - Tables de hachage de largeur fixée

type ('a, 'b) table_hachage = {
    hache: 'a -> int;
    donnees: ('a * 'b) list vect;
    largeur: int};;

III.B.1) Implantation de la structure de dictionnaire

III.B.2) Étude de la complexité de la recherche d'un élément

III.C - Tables de hachage dynamique

type ('a,'b) table_dyn = {
    hache: int -> 'a -> int;
    mutable taille: int;
    mutable donnees: ('a * 'b) list vect;
    mutable largeur: int};;

• la fonction hache possède un paramètre supplémentaire qui est la largeur de hachage, elle correspond maintenant à la famille de fonctions de hachage ( );
• on a rendu les champs donnees et largeur modifiables;
• un champ taille (modifiable) est rajouté, il doit à tout moment contenir le nombre de clés présentes dans la table.
  Q 20. Écrire une fonction creer_table_dyn h permettant de créer une table de hachage dynamique initialement vide, avec la famille de fonctions de hachage et la largeur initiale 1.
  On admet avoir écrit deux fonctions recherche_dyn et element_dyn , variantes des fonctions recherche et element précédentes, basées sur le même principe. On va maintenant développer une stratégie pour maintenir à tout moment un facteur de remplissage borné.
  Q 21. Écrire une fonction rearrange_dyn t w2 prenant en entrée une table de hachage dynamique et une nouvelle largeur de hachage w2, qui réarrange la table sur une largeur w2. En supposant que le calcul des valeurs de hachage se fasse en temps constant, la complexité doit être en où est le nombre de clés présentes dans la table (sa taille), est l'ancienne largeur de la table, la nouvelle.
  Une stratégie heuristique simple pour garantir que le facteur de remplissage reste borné, tout en garantissant une bonne répartition des clés dans le cas des listes de couples à valeurs dans avec , est d'utiliser les puissances de 3 comme largeurs de hachage. Après ajout d'un élément à la table, si celle-ci est de taille strictement supérieure à trois fois sa largeur , on la réarrange sur une largeur .
  Q 22. Écrire une fonction ajout_dyn t k e ajoutant le couple ( ) à la table de hachage (si la clé n'est pas présente), en réarrangeant si nécessaire la table, en suivant le principe ci-dessus.
  Dans l'hypothèse que chaque ajout se fait en temps , où est le facteur de remplissage de la table, on peut montrer qu'une série de ajouts dans une table initialement vide prend un temps .
  On pourrait écrire de même une fonction de suppression dynamique, de sorte de maintenir un facteur de remplissage de la table borné, et qu'une série de opérations licites d'insertion/suppression dans la table prenne un temps .

IV Résolution du jeu des robots

IV.A - Graphe orienté associé au jeu des robots

type sommet = {robot: int * int; autres_robots: (int * int) list};;

IV.B - Parcours en largeur : étude théorique

Entrées : un arbre $G=(S, A)$, orienté, un sommet de départ $s_{0}$
Sortie : un tableau de booléens, un tableau de prédecesseurs
$F \leftarrow$ creer_file_vide () ;
Enfiler $s_{0}$ dans $F$;
$b_{s_{0}} \leftarrow$ vrai ;
$b_{s} \leftarrow$ faux pour tout $s \in S$; (* un tableau de booléens pour chaque sommet, tous faux *)
$\pi_{s} \leftarrow s$ pour tout $s \in S$; (* un tableau de prédecesseurs pour chaque sommet, initialement $\pi[s]=s^{*}$ )
tant que $F$ est non vide faire
    $s \leftarrow \operatorname{defiler}(F) ;$
    pour tout $s^{\prime}$ voisin de $s$ tel que $b_{s^{\prime}}$ est faux faire
        $b_{s^{\prime}} \leftarrow$ vrai $; \pi_{s^{\prime}} \leftarrow s$; enfiler $s^{\prime}$ dans $F$;
    fin pour
fin tant que
renvoyer $b, \pi$

Algorithme 1 Parcours en largeur