Version interactive avec LaTeX compilé
Centrale Option Informatique MP 2017
Mots synchronisants
Notez ce sujet en cliquant sur l'étoile
0.0(0 votes)
Mots synchronisants
Notations
- Pour tout ensemble fini
, on note son cardinal. - On appelle machine tout triplet (
) où est un ensemble fini non vide dont les éléments sont appelés états, un ensemble fini non vide appelé alphabet dont les éléments sont appelés lettres et une application de dans appelée fonction de transition. Une machine correspond donc à un automate déterministe complet sans notion d'état initial ou d'états finaux. - Pour un état
et une lettre , on note . - L'ensemble des mots (c'est-à-dire des concaténations de lettres) sur l'alphabet
est noté . - Le mot vide est noté
. - On note
le mot obtenu par la concaténation du mot et de la lettre . - On note
l'extension à de la fonction de transition définie par
- Pour un état
de et un mot de , on note encore pour désigner .
Pour deux états
On dit qu'un mot
L'existence de tels mots dans certaines machines est utile car elle permet de ramener une machine dans un état particulier connu en lisant un mot donné (donc en pratique de la « réinitialiser » par une succession précise d'ordres passés à la machine réelle).
La partie I de ce problème étudie quelques considérations générales sur les mots synchronisants, la partie II est consacrée à des problèmes algorithmiques classiques, la partie III relie le problème de la satisfiabilité d'une formule logique à celui de la recherche d'un mot synchronisant de longueur donnée dans une certaine machine et enfin la partie IV s'intéresse à l'étude de l'existence d'un mot synchronisant pour une machine donnée. Les parties I, II et III peuvent être traitées indépendamment. La partie IV, plus technique, utilise la partie II.
Dans les exemples concrets de machines donnés plus loin, l'ensemble d'états peut être quelconque, de même que l'alphabet (
On dit qu'un mot
L'existence de tels mots dans certaines machines est utile car elle permet de ramener une machine dans un état particulier connu en lisant un mot donné (donc en pratique de la « réinitialiser » par une succession précise d'ordres passés à la machine réelle).
La partie I de ce problème étudie quelques considérations générales sur les mots synchronisants, la partie II est consacrée à des problèmes algorithmiques classiques, la partie III relie le problème de la satisfiabilité d'une formule logique à celui de la recherche d'un mot synchronisant de longueur donnée dans une certaine machine et enfin la partie IV s'intéresse à l'étude de l'existence d'un mot synchronisant pour une machine donnée. Les parties I, II et III peuvent être traitées indépendamment. La partie IV, plus technique, utilise la partie II.
Dans les exemples concrets de machines donnés plus loin, l'ensemble d'états peut être quelconque, de même que l'alphabet (
type lettre == int;;
type mot == lettre list;;
De même, en Caml, l'ensemble d'états
type etat == int;;
Ainsi, la fonction de transition
type machine = { n_etats : int ; n_lettres : int ; delta : etat -> lettre -> etat} ; ;
n_etats correspond au cardinal de
Par exemple, on peut créer une machine MO à trois états sur un alphabet à deux lettres ayant comme fonction de transition la fonction
Par exemple, on peut créer une machine MO à trois états sur un alphabet à deux lettres ayant comme fonction de transition la fonction
let fO etat lettre = match etat,lettre with
| 0,0 -> 1
| 0,1 -> 1
| 1,0 -> 0
| 1,1 -> 2
| 2,0 -> 0
| 2,1 -> 2;;
fO : int -> int -> int = <fun>
let MO = { n_etats = 3 ; n_lettres = 2 ; delta = f0 };;
La figure 1 fournit une représentation de la machine
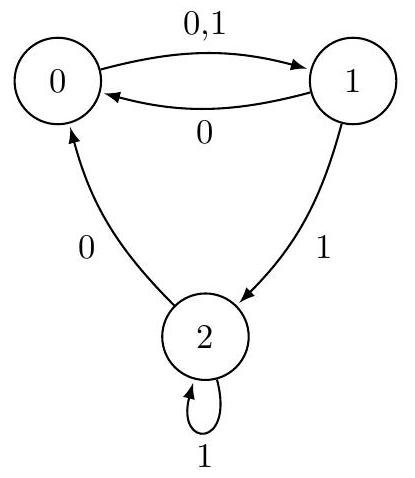
Figure 1 La machine
On pourra observer que les mots 11 et 10 sont tous les deux synchronisants pour la machine
Dans tout le sujet, si une question demande la complexité d'un programme ou d'un algorithme, on attend une complexité temporelle exprimée en
Dans tout le sujet, si une question demande la complexité d'un programme ou d'un algorithme, on attend une complexité temporelle exprimée en
I Considérations générales
I.
Dans toute la suite du problème, on supposera que les machines ont au moins deux états.
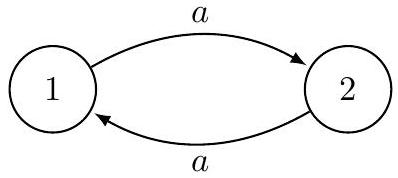
Figure 2 La machine
I.E - Écrire une fonction est_synchronisant de signature machine
I.F - Montrer que pour qu'une machine ait un mot synchronisant, il faut qu'il existe une lettre
I.
I.G.1) Justifier que l'existence d'un mot synchronisant pour
I.G.2) En déduire que le langage
I.G.2) En déduire que le langage
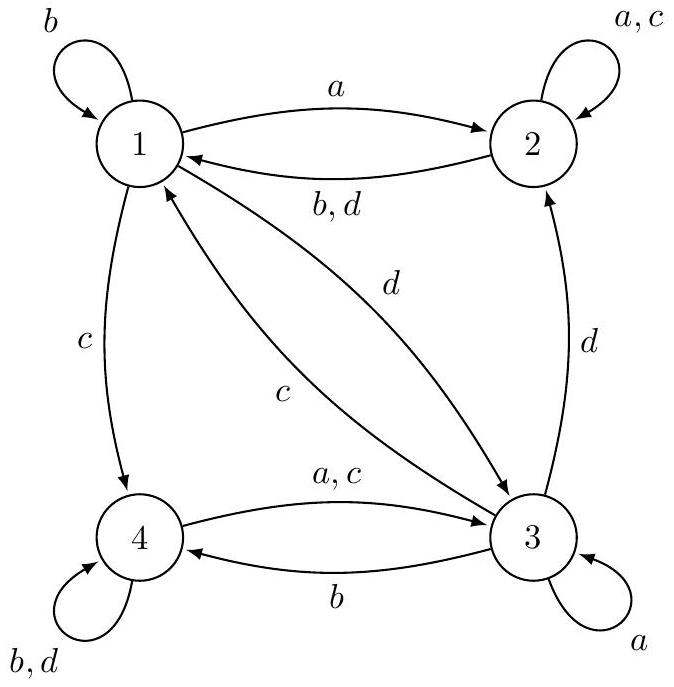
Figure
I.G.3) Déterminer la machine des parties associée à la machine
I.H - Montrer que si l'on sait résoudre le problème de l'existence d'un mot synchronisant, on sait dire, pour une machine
I.H - Montrer que si l'on sait résoudre le problème de l'existence d'un mot synchronisant, on sait dire, pour une machine
II Algorithmes classiques
On appellera graphe d'automate tout couple (
Par exemple, avec
Par exemple, avec
le graphe d'automate
Soient
Soient
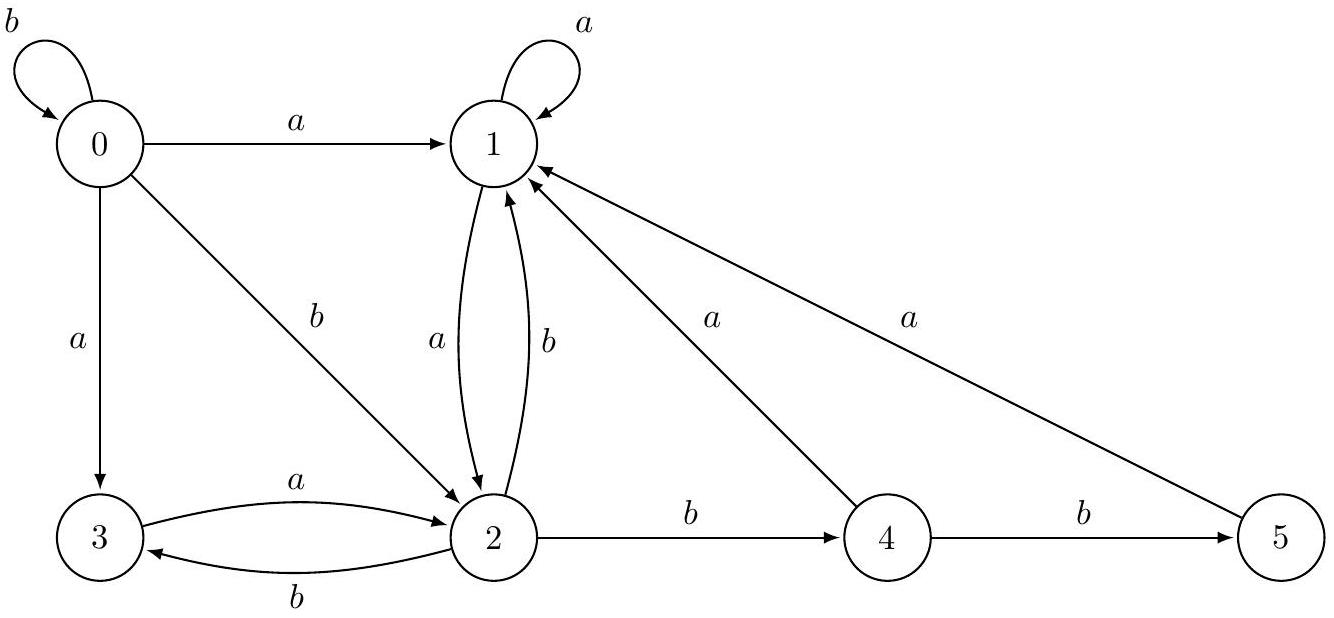
Figure 4 Le graphe d'automate
Dans les programmes à écrire, un graphe aura toujours pour ensemble de sommets un intervalle d'entiers
Ainsi, avec l'alphabet
Ainsi, avec l'alphabet
V0 : (etat * lettre) list vect = [|
[(0,1) ; (3,0) ; (2,1) ; (1,0)] ;
[(1,0) ; (2,0)] ;
[(1,1); (3,1); (4,1)];
[(2,0)] ;
[(1,0) ; (5,1)] ;
[(1,0)]
|]
II.A - On veut implémenter une file d'attente à l'aide d'un vecteur circulaire. On définit pour cela un type particulier nommé file par
type 'a file={tab:'a vect; mutable deb: int; mutable fin: int; mutable vide: bool}
deb indique l'indice du premier élément dans la file et fin l'indice qui suit celui du dernier élément de la file, vide indiquant si la file est vide. Les éléments sont rangés depuis la case deb jusqu'à la case précédent fin en repartant à la case 0 quand on arrive au bout du vecteur (cf exemple). Ainsi, on peut très bien avoir l'indice fin plus petit que l'indice deb. Par exemple, la file figure 5 contient les éléments
type 'a file={tab:'a vect; mutable deb: int; mutable fin: int; mutable vide: bool}
deb indique l'indice du premier élément dans la file et fin l'indice qui suit celui du dernier élément de la file, vide indiquant si la file est vide. Les éléments sont rangés depuis la case deb jusqu'à la case précédent fin en repartant à la case 0 quand on arrive au bout du vecteur (cf exemple). Ainsi, on peut très bien avoir l'indice fin plus petit que l'indice deb. Par exemple, la file figure 5 contient les éléments

Figure 5 Un exemple de file où fin < deb
On rappelle qu'un champ mutable peut voir sa valeur modifiée. Par exemple, la syntaxe f .deb <- 0 affecte la valeur 0 au champ deb de la file
II.A.1) Écrire une fonction ajoute de signature 'a file
II.A.2) Écrire une fonction retire de signature 'a file
II.A.3) Quelle est la complexité de ces fonctions ?
II.A.1) Écrire une fonction ajoute de signature 'a file
II.A.2) Écrire une fonction retire de signature 'a file
II.A.3) Quelle est la complexité de ces fonctions ?
On considère l'algorithme 1 s'appliquant à un graphe d'automate
II.B - Justifier que l'algorithme 1 termine toujours.
II.
II.D - Justifier qu'au début de chaque passage dans la boucle «tant que
II.E - Pour
II.E.1) Justifier brièvement qu'à la fin de l'algorithme, pour tout sommet
II.E.2) Montrer qu'en fait, à la fin, on a pour tout sommet
II.F - Écrire une fonction accessibles de signature
II.B - Justifier que l'algorithme 1 termine toujours.
II.
II.D - Justifier qu'au début de chaque passage dans la boucle «tant que
II.E - Pour
II.E.1) Justifier brièvement qu'à la fin de l'algorithme, pour tout sommet
II.E.2) Montrer qu'en fait, à la fin, on a pour tout sommet
II.F - Écrire une fonction accessibles de signature
((etat*lettre) list) vect -> etat list -> int * int vect * (etat*lettre) vect
prenant en entrée un graphe d'automate (sous la forme de son vecteur de listes d'adjacence V) et un ensemble E de sommets (sous la forme d'une liste d'états) et qui renvoie le triplet (
créer une file d'attente $F$, vide au départ
créer un tableau $D$ dont les cases sont indexées par $S$ et initialisées à $\infty$
créer un tableau $P$ dont les cases sont indexées par $S$ et initialisées à vide
créer une variable $c$ initialisée à $n$
pour tout $s \in E$ faire
insérer $s$ à la fin de la file d'attente $F$
fixer $D[s]$ à 0
fixer $P[s]$ à rien
diminuer $c$ de 1
fin pour
tant que $F$ n'est pas vide faire
extraire le sommet $s$ qui est en tête de $F$
pour tout arc $\left(s, y, s^{\prime}\right) \in A$ tel que $D\left[s^{\prime}\right]=\infty$ faire
fixer $D\left[s^{\prime}\right]$ à $D[s]+1$
fixer $P\left[s^{\prime}\right]$ à $(s, y)$
insérer $s^{\prime}$ à la fin de la file d'attente $F$
diminuer $c$ de 1
fin pour
fin tant que
renvoyer ( $c, D, P$ )
Algorithme 1
II.G - Écrire une fonction chemin de signature etat
III Réduction SAT
On s'intéresse dans cette partie à la satisfiabilité d'une formule logique portant sur des variables propositionnelles
On appelle littéral une formule constituée d'une variable
Considérons une formule logique sous forme normale conjonctive c'est-à-dire sous la forme d'une conjonction de clauses. Par exemple,
On appelle littéral une formule constituée d'une variable
Considérons une formule logique sous forme normale conjonctive c'est-à-dire sous la forme d'une conjonction de clauses. Par exemple,
est une formule sous forme normale conjonctive formée de trois clauses et portant sur quatre variables propositionnelles
Soit
Soit
-
est formé de états, un état particulier noté et autres états qu'on notera avec
; -
est défini par -
est un état puits, c'est-à-dire , - pour tout entier
de , - pour tout
dans et dans ,
III.
III.
III.
III.
III.
III.
III.
III.
III.
IV Existence
On reprend dans cette partie le problème de l'existence d'un mot synchronisant pour une machine
IV.A - Soit
IV.A - Soit
Pour toute partie
IV.A.1) Soit
IV.A.2) Montrer qu'il existe un mot synchronisant si et seulement s'il existe pour tout couple d'états (
On veut se servir du critère établi ci-dessus pour déterminer s'il existe un mot synchronisant. Pour cela, on associe à la machine
IV.A.1) Soit
IV.A.2) Montrer qu'il existe un mot synchronisant si et seulement s'il existe pour tout couple d'états (
On veut se servir du critère établi ci-dessus pour déterminer s'il existe un mot synchronisant. Pour cela, on associe à la machine
-
est formé des parties à un ou deux éléments de ; -
est définie par .
Si , que vaut ?
IV.C - On a dit que pour la modélisation informatique, l'ensemble d'états d'une machine doit être modélisée par un intervalle. doit donc être modélisé par l'intervalle . Soit une bijection de sur . On suppose qu'on dispose d'une fonction set_to_nb de signature int (etat list) -> etat telle que set_to_nb pour élément de et liste d'états renvoie
On suppose qu'on dispose aussi d'une fonction réciproque nb_to_set de signature int
Enfin, pour ne pas confondre un état de
Écrire une fonction delta2 de signature machine
IV.D - Il est clair qu'à la machine
Écrire une fonction retourne_machine de signature machine
IV.E - Justifier qu'il suffit d'appliquer la fonction accessibles de la partie II au graphe
IV.F - Écrire une fonction existe_synchronisant de signature machine
Enfin, pour ne pas confondre un état de
Écrire une fonction delta2 de signature machine
IV.D - Il est clair qu'à la machine
Écrire une fonction retourne_machine de signature machine
IV.E - Justifier qu'il suffit d'appliquer la fonction accessibles de la partie II au graphe
IV.F - Écrire une fonction existe_synchronisant de signature machine
Jan Černý, chercheur slovaque, a conjecturé au milieu des années 60 que si une machine à n états possédait un mot synchronisant, elle en avait un de longueur inférieure ou égale
