Version interactive avec LaTeX compilé
Le sujet est composé de deux parties indépendantes, la première utilise le langage C et la seconde le langage OCaml. Toutes deux traitent de graphes.
La première se concentre sur un problème classique, le problème du voyageur de commerce. Elle étudie d'abord sa complexité, en le comparant notamment au problème très proche du cycle et du chemin hamiltonien, puis en le réduisant à 3-SAT, et en donnant un résultat sur l'approximabilité du problème. On propose ensuite une heuristique, l'algorithme de Christofides, qui repose sur différentes notions : arbres couvrants, couplages, circuit eulérien. On montrera que, dans une variante du problème où les distances vérifient l'inégalité triangulaire, l'algorithme de Christofides est une approximation de facteur
La deuxième partie s'intéresse à des processus d'édition sur des arbres non racinés dont les feuilles sont étiquetées, qui sont notamment utilisés en bio-informatique pour représenter l'évolution des espèces. On étudiera en particulier l'espace induit sur ces arbres par ces processus d'édition et on représentera cet espace par un graphe. On montrera notamment que le graphe induit par l'un de ces processus d'édition possède un cycle hamiltonien. On utilisera pour cette partie le langage OCaml pour implémenter des arbres par une définition récursive et des graphes par liste d'adjacence.
I Problème du voyageur de commerce
On considère des graphes non orientés
Un chemin est une suite de sommets reliés par des arêtes. On dit qu'un chemin passe par un sommet si ce sommet appartient au chemin. Un circuit est un chemin qui commence et se termine au même sommet. Un chemin hamiltonien est un chemin qui passe une et une seule fois par chaque sommet du graphe. Un circuit hamiltonien est un circuit qui passe par chaque sommet une et une seule fois.
Le problème du voyageur de commerce consiste, étant donnée une liste de villes toutes reliées entre elles, à trouver le circuit le plus court qui passe une et une seule fois par chacune des villes.
Plus formellement, on considère un graphe complet non orienté, dont les arêtes sont étiquetées avec des nombres entiers strictement positifs, appelés poids, et on cherche le circuit passant par chacun des sommets du graphe qui minimise la somme des poids des arêtes. On appellera poids d'un circuit la somme des poids des arêtes empruntées par ce circuit. Une solution au problème du voyageur de commerce est un circuit hamiltonien de poids minimal.
Dans cette partie, on représente les graphes en C par des matrices d'adjacence. Le poids d'une arête est représenté par un int, une arête absente étant représentée par un 0 . On représente un graphe par une structure de données avec deux attributs : son nombre de sommets V et un pointeur adj vers sa matrice d'adjacence de taille
Un chemin est une suite de sommets reliés par des arêtes. On dit qu'un chemin passe par un sommet si ce sommet appartient au chemin. Un circuit est un chemin qui commence et se termine au même sommet. Un chemin hamiltonien est un chemin qui passe une et une seule fois par chaque sommet du graphe. Un circuit hamiltonien est un circuit qui passe par chaque sommet une et une seule fois.
Le problème du voyageur de commerce consiste, étant donnée une liste de villes toutes reliées entre elles, à trouver le circuit le plus court qui passe une et une seule fois par chacune des villes.
Plus formellement, on considère un graphe complet non orienté, dont les arêtes sont étiquetées avec des nombres entiers strictement positifs, appelés poids, et on cherche le circuit passant par chacun des sommets du graphe qui minimise la somme des poids des arêtes. On appellera poids d'un circuit la somme des poids des arêtes empruntées par ce circuit. Une solution au problème du voyageur de commerce est un circuit hamiltonien de poids minimal.
Dans cette partie, on représente les graphes en C par des matrices d'adjacence. Le poids d'une arête est représenté par un int, une arête absente étant représentée par un 0 . On représente un graphe par une structure de données avec deux attributs : son nombre de sommets V et un pointeur adj vers sa matrice d'adjacence de taille
struct Graphe {
int V;
int* adj;
};
Pour accéder au poids de l'arête entre le sommet i et le sommet j du graphe G, on pourra utiliser l'expression G.adj[i * G.V + j].
On pourra par la suite utiliser les deux fonctions suivantes, qui sont supposées travailler en temps constant :
struct Graphe alloue_graphe(int V) {
int* adj = malloc(V * V * sizeof(int));
struct Graphe g = {.V = V, .adj = adj};
return g;
}
void libere_graphe(struct Graphe g) {
free(g.adj);
}
La fonction alloue_graphe prend comme argument un nombre V et renvoie un graphe qui possède V sommets et dont la matrice d'adjacence est allouée sur le tas, grâce à la fonction malloc. La fonction libere_graphe libère la mémoire du tas occupée par la matrice d'adjacence d'un graphe dont on n'a plus besoin.
On définit également une structure Chemin qui représente un chemin par un attribut longueur et un attribut l_sommets, pointeur vers un tableau à longueur éléments. Si C est un chemin et k un entier naturel strictement plus petit que C.longueur, alors C.l_sommets [k] est le k-ième sommet du chemin C. De même que pour les graphes, on définit aussi des fonctions permettant d'allouer un chemin et de libérer un chemin dont on n'a plus besoin, et qui sont supposées travailler en temps constant.
On définit également une structure Chemin qui représente un chemin par un attribut longueur et un attribut l_sommets, pointeur vers un tableau à longueur éléments. Si C est un chemin et k un entier naturel strictement plus petit que C.longueur, alors C.l_sommets [k] est le k-ième sommet du chemin C. De même que pour les graphes, on définit aussi des fonctions permettant d'allouer un chemin et de libérer un chemin dont on n'a plus besoin, et qui sont supposées travailler en temps constant.
struct Chemin {
int longueur;
int* l_sommets;
};
struct Chemin alloue_chemin(int longueur) {
int* l_sommets = malloc(longueur * sizeof(int));
struct Chemin c = {.longueur = longueur, .l_sommets = l_sommets};
return c;
}
void libere_chemin(struct Chemin c) {
free(c.l_sommets);
}
I.A - Prise en main du problème et appartenance à NP
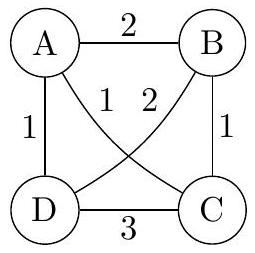
Figure 1 Exemple d'instance du problème du voyageur de commerce
Q 1. Donner une solution du problème du voyageur de commerce sur l'exemple de la figure 1 en précisant le poids du circuit trouvé.
Q 2. Donner le nombre de circuits hamiltoniens sur un graphe complet de
Q 3. Écrire une fonction
int poids_chemin(struct Graphe g, struct Chemin c);
qui prend en arguments un graphe et un chemin et renvoie le poids de ce chemin. Donner la complexité de cette fonction.
Q 4. Le problème du voyageur de commerce est un problème d'optimisation ; à l'aide d'un seuil, transformer ce problème en un problème de décision. Montrer que ce nouveau problème, que nous appellerons par la suite «problème de décision du voyageur de commerce», appartient à la classe de complexité NP.
Q 2. Donner le nombre de circuits hamiltoniens sur un graphe complet de
Q 3. Écrire une fonction
int poids_chemin(struct Graphe g, struct Chemin c);
qui prend en arguments un graphe et un chemin et renvoie le poids de ce chemin. Donner la complexité de cette fonction.
Q 4. Le problème du voyageur de commerce est un problème d'optimisation ; à l'aide d'un seuil, transformer ce problème en un problème de décision. Montrer que ce nouveau problème, que nous appellerons par la suite «problème de décision du voyageur de commerce», appartient à la classe de complexité NP.
I.B - Étude de la complexité
Le problème du chemin hamiltonien consiste, étant donné un graphe non orienté et deux sommets
I.B.1) NP-complétude
Q 5. Montrer que le problème du chemin hamiltonien se réduit au problème du circuit hamiltonien.
Q 6. Montrer que le problème du circuit hamiltonien se réduit au problème de décision du voyageur de commerce.
Q 7. Montrer que le problème du chemin hamiltonien orienté se réduit au problème du chemin hamiltonien. Le problème 3-SAT consiste à déterminer la satisfiabilité d'une formule logique sous forme normale conjonctive avec exactement 3 littéraux : pour
Q 6. Montrer que le problème du circuit hamiltonien se réduit au problème de décision du voyageur de commerce.
Q 7. Montrer que le problème du chemin hamiltonien orienté se réduit au problème du chemin hamiltonien. Le problème 3-SAT consiste à déterminer la satisfiabilité d'une formule logique sous forme normale conjonctive avec exactement 3 littéraux : pour
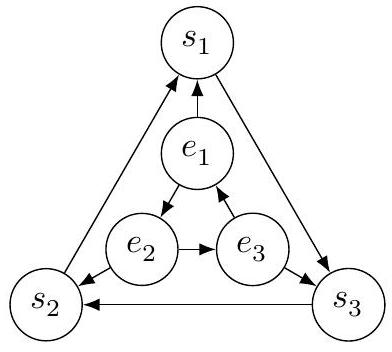
Figure 2 Graphe
Q 8. On considère le graphe
On se donne une instance du problème 3-SAT, pour
On construit alors le graphe orienté
On se donne une instance du problème 3-SAT, pour
On construit alors le graphe orienté
- pour chaque variable
on crée un sommet ; - on ajoute un sommet supplémentaire
; - pour chaque clause
on ajoute une copie du graphe , notée ; - pour chaque variable
, on note les clauses dans lesquelles apparait en positif. On relie alors à par un arc allant de vers dans lorsque est en position dans c'est-à-dire lorsque et . On relie ensuite la sortie de à l'entrée de correspondant à la position de dans et ainsi de suite jusqu'au dernier dont on relie la sortie à . On appelle le sous-graphe constitué du sommet , des graphes et du sommet , ainsi que des arcs que l'on vient d'ajouter entre eux en considérant et les clauses dans lesquelles il apparait positivement ; - on crée de même des arcs pour chaque variable
et chaque clause dans laquelle apparait en négatif. On note , le sous-graphe correspondant entre et .
Q 9. Montrer que pour toute valuation de la formule il existe un chemin hamiltonien orienté deà dans le graphe .
Q 10. Montrer, en une dizaine de lignes au maximum, que pour chaque chemin hamiltonien orienté deà il existe bien une valuation.
Q 11. En déduire que le problème du circuit hamiltonien et le problème de décision du voyageur de commerce sont NP-complets.
I.B.2) Approximation
Soit
Soit
Q 12. Montrer que si
Q 13. Montrer que si
Q 14. En déduire que, si
Soit
Q 12. Montrer que si
Q 13. Montrer que si
Q 14. En déduire que, si
I.C - Algorithme de Christofides
On va proposer une heuristique pour le problème du voyageur de commerce, l'algorithme de Christofides, et on va montrer que, sous certaines conditions sur le graphe en entrée, cette heuristique constitue un algorithme d'approximation. L'algorithme prend en argument un graphe
- calculer un arbre couvrant de poids minimal
de ; - en notant
l'ensemble des sommets de degré impair dans , calculer un couplage parfait de poids minimum dans le sous-graphe de induit par les sommets de ; - construire
le multigraphe ayant pour sommet les sommets de et comme arêtes les arêtes de et celles de ; - trouver un cycle eulérien dans
; - transformer le cycle eulérien en circuit hamiltonien en supprimant les éventuels sommets vus plusieurs fois.
Dans la suite, on étudie plus précisément certaines étapes de cet algorithme, avant de proposer une implémentation de cet algorithme.
I.C.1) Arbre couvrant
Un arbre couvrant est un sous-graphe connexe sans cycle d'un graphe avec les mêmes sommets. On appelle poids de l'arbre la somme des poids des arêtes de cet arbre. On rappelle que l'algorithme de Kruskal est un algorithme glouton qui vise à construire un arbre couvrant de poids minimal en considérant les arêtes par poids croissant et en ajoutant chaque arête si elle ne crée pas de cycle.
Pour cela, on va représenter une arête par une structure de données avec trois attributs : s1 et s2 donnent les sommets reliés par l'arête et
Pour cela, on va représenter une arête par une structure de données avec trois attributs : s1 et s2 donnent les sommets reliés par l'arête et
struct Arete {
int s1;
int s2;
int p;
};
Q 15. Écrire une fonction
struct Arete* liste_aretes(struct Graphe g);
qui prend en argument un graphe complet
On dispose d'une fonction
void tri_aretes(struct Arete a[], int k);
qui prend en arguments un tableau d'arêtes et sa longueur et trie le tableau par ordre croissant de poids. La complexité de cette fonction est en
Q 16. Écrire une fonction
struct Graphe kruskal(struct Graphe g);
implémentant l'algorithme de Kruskal qui renvoie un graphe représentant l'arbre couvrant de poids minimal du graphe donné en argument. On mettra des 0 lorsque l'arête est absente et des 1 lorsqu'elle est présente. Donner la complexité de la fonction kruskal.
Q 17. Montrer la correction de cet algorithme, c'est-à-dire l'optimalité de la solution proposée pour le problème d'arbre couvrant de poids minimal.
Q 17. Montrer la correction de cet algorithme, c'est-à-dire l'optimalité de la solution proposée pour le problème d'arbre couvrant de poids minimal.
I.C.2) Couplage
On appelle couplage d'un graphe un ensemble d'arêtes qui n'ont pas de sommets en commun. Un couplage est parfait si tous les sommets du graphe appartiennent à une arête du couplage.
Q 18. Écrire une fonction
int degre(struct Graphe g, int i);
qui prend en arguments un graphe et l'indice d'un sommet et renvoie le degré de ce sommet.
Q 19. Écrire une fonction
int* sommets_impairs(struct Graphe g, int* nb_sommets);
qui prend en arguments un graphe
Q 20. Montrer l'existence d'un couplage parfait de poids minimal dans
On dispose des deux fonctions suivantes:
Q 20. Montrer l'existence d'un couplage parfait de poids minimal dans
On dispose des deux fonctions suivantes:
struct Graphe graphe_induit(struct Graphe g, int nb_sommets, int* liste_sommets);
struct Graphe couplage(struct Graphe g);
La fonction graphe_induit renvoie le graphe induit dans un graphe g donné par un nombre et un tableau de sommets comme ceux de la question 19.
La fonction couplage renvoie un couplage parfait de poids minimal s'il existe, sous la forme d'un graphe représentant ce couplage, avec des 0 lorsque l'arête est absente et 1 lorsque l'arête est présente.
On supposera ces deux fonctions de complexité polynomiale.
La fonction couplage renvoie un couplage parfait de poids minimal s'il existe, sous la forme d'un graphe représentant ce couplage, avec des 0 lorsque l'arête est absente et 1 lorsque l'arête est présente.
On supposera ces deux fonctions de complexité polynomiale.
I.C.3) Cycle eulérien
On appelle cycle eulérien un circuit qui passe par chaque arête une et une unique fois. On admet qu'un graphe possède un cycle eulérien si et seulement les degrés des sommets de ce graphe sont pairs et que le graphe est connexe. Un multigraphe est un graphe dans lequel il peut exister plusieurs arêtes reliant un même couple de sommets.
Q 21. Montrer que le multigraphe
On dispose des trois fonctions suivantes:
Q 21. Montrer que le multigraphe
On dispose des trois fonctions suivantes:
struct Multigraphe multigraphe(struct Graphe g1, struct Graphe g2);
struct Chemin eulerien(struct Multigraphe h);
void libere_multigraphe(struct Multigraphe h);
La fonction multigraphe prend en arguments deux graphes sur les mêmes sommets et renvoie le multigraphe obtenu en considérant les arêtes des deux graphes. La fonction eulerien renvoie un circuit eulérien d'un multigraphe sous la forme d'un chemin. La fonction libere_multigraphe libère la mémoire du tas utilisée par un multigraphe. Toutes trois sont supposées de complexité polynomiale.
Q 22. Écrire une fonction
struct Chemin euler_to_hamilton(struct Chemin c);
qui transforme un cycle eulérien c du multigraphe
I.C.4) Implémentation
Q 23. Sur l'exemple de la figure 1, réaliser les différentes étapes de l'algorithme. On ne demande pas de détailler les étapes pour trouver un couplage et un cycle eulérien.
Q 24. Écrire une fonction
struct Chemin christofides(struct Graphe g);
qui implémente l'algorithme de Christofides, en prenant soin de libérer la mémoire allouée sur le tas qui n'est plus utilisée.
Q 25. Justifier que la fonction christophides renvoie bien un circuit hamiltonien.
Q 26. Montrer que la fonction christophides est de complexité polynomiale.
Q 25. Justifier que la fonction christophides renvoie bien un circuit hamiltonien.
Q 26. Montrer que la fonction christophides est de complexité polynomiale.
I.C.5) Preuve de l'approximation
On va maintenant montrer que cet algorithme est une
Q 27. Montrer que
Q 28. Montrer que
Q 29. Montrer que la solution construite par l'algorithme est une
Q 30. Sans la supposition de l'inégalité triangulaire, cette solution est-elle toujours une
Q 27. Montrer que
Q 28. Montrer que
Q 29. Montrer que la solution construite par l'algorithme est une
Q 30. Sans la supposition de l'inégalité triangulaire, cette solution est-elle toujours une
II Espaces d'arbres
Dans cette partie on considère des arbres binaires non racinés avec des feuilles étiquetées. Un arbre binaire non raciné est un graphe connexe sans cycle dont les nœuds sont de degrés 1 ou 3 . Un arbre binaire raciné est un graphe connexe sans cycle dont les nœuds sont de degrés 1 ou 3 sauf exactement un nœud qui est de degré 2 . Les nœuds de degré 1 sont appelés des feuilles, les nœuds de degré 2 ou 3 des nœuds internes et l'unique nœud de degré 2 d'un arbre binaire raciné est appelé sa racine. Un graphe réduit à un unique nœud est considéré comme un arbre raciné dont le nœud est à la fois feuille et racine. Les arêtes d'un arbre sont appelées des branches, les branches reliant des sommets de degré 2 ou 3 branches internes. On étiquette ensuite les feuilles d'un arbre à
La première opération, notée SPR, pour Subtree Prune and Regraft (ou découpe et greffe d'un sous-arbre), prend en entrée 2 branches
La première opération, notée SPR, pour Subtree Prune and Regraft (ou découpe et greffe d'un sous-arbre), prend en entrée 2 branches
On s'intéresse également à une autre opération, notée NNI, pour Nearest Neighbor Interchange (ou échange entre plus proches voisins). Cette opération prend une branche interne de l'arbre
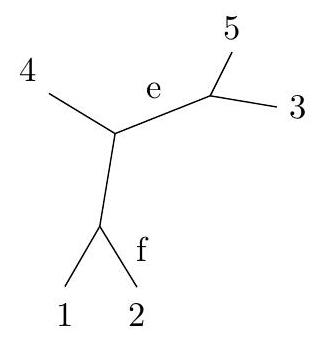
Arbre 1
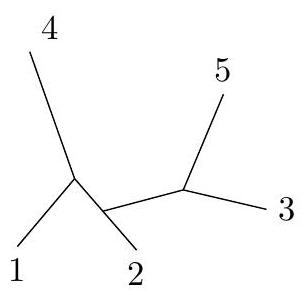
Arbre 2
Arbre 3
Arbre 4
Arbre 5
Figure 3 Exemples d'arbres non racinés
La figure 3 présente quelques exemples d'arbres non racinés :
- l'arbre 1 est un arbre binaire non raciné avec ses feuilles étiquetées ;
- l'arbre 2 est obtenu à partir de l'arbre 1 par un SPR en coupant la branche
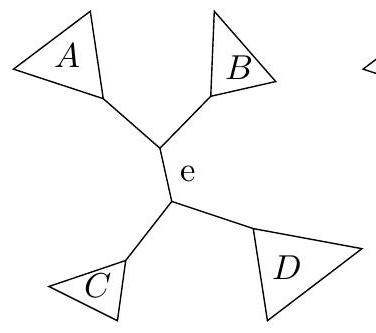
et en la greffant sur la branche ; - dans l'arbre 3 , où les triangles représentent des sous-arbres racinés, la branche interne
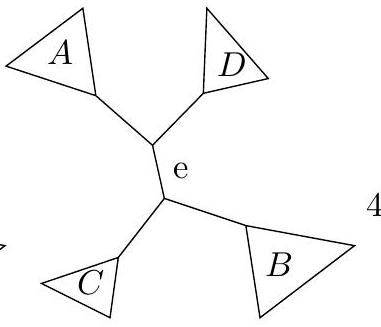
sépare 4 sous-arbres racinés et D ; - l'arbre 4 est obtenu à partir de l'arbre 3 par un mouvement NNI sur la branche
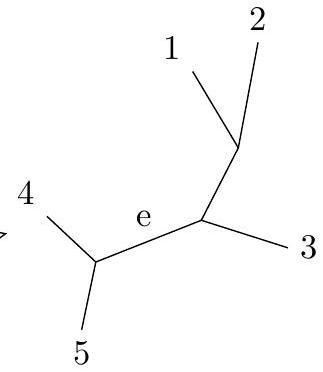
en échangeant les sous-arbres B et D ; - l'arbre 5 est obtenu à partir de l'arbre 1 par un NNI sur la branche
en échangeant le sous-arbre contenant la feuille 5 et le sous-arbre contenant les feuilles 1 et 2 .
On étudie l'espace des arbres binaires non racinés étiquetés defeuilles suivant ces deux processus d'édition. On définit le graphe dont les sommets sont les arbres de et dans lequel une arête relie deux arbres si l'on peut passer de l'un à l'autre par un mouvement NNI. On définit de même avec les mouvements SPR. On va notamment s'intéresser à la structure de , écrire un programme permettant de construire et montrer que est hamiltonien, c'est-à-dire qu'il possède un circuit hamiltonien.
II.A - Prise en main
Q 31. Montrer que l'on peut passer de l'arbre 1 à l'arbre 2 par une opération NNI. Dessiner tous les voisins de l'arbre 1 dans
Q 32. Donner le nombre de branches et de nœuds d'un arbre de
Q 33. On note
Q 34. Tracer
Q 35. Combien de voisins un arbre de
On appelle arbre chenille un arbre binaire non raciné dans lequel il existe un chemin passant une et une seule fois par chaque nœud interne.
Q 36. Montrer que l'on peut passer de tout arbre de
Q 37. Montrer que tout mouvement SPR peut se décomposer en mouvements NNI, et que tous les mouvements NNI sont des mouvements SPR. En déduire que
Q 32. Donner le nombre de branches et de nœuds d'un arbre de
Q 33. On note
Q 34. Tracer
Q 35. Combien de voisins un arbre de
On appelle arbre chenille un arbre binaire non raciné dans lequel il existe un chemin passant une et une seule fois par chaque nœud interne.
Q 36. Montrer que l'on peut passer de tout arbre de
Q 37. Montrer que tout mouvement SPR peut se décomposer en mouvements NNI, et que tous les mouvements NNI sont des mouvements SPR. En déduire que
II.B - Étude de
Q 38. Combien de sommets possède
Q 39. Montrer que tout arbre de
Q 40. Tracer
Q 39. Montrer que tout arbre de
Q 40. Tracer
II.C - Construction de
On va écrire en OCaml un programme qui construit
type arbre = Feuille of int
| Noeud of arbre * arbre ;;
Un arbre raciné est alors représenté par sa racine, qui peut être soit une feuille soit un nœud interne ayant un sous-arbre gauche et un sous-arbre droit.
Un arbre non raciné à
Enfin, pour assurer l'unicité de la représentation informatique d'un arbre, et ainsi simplifier les programmes, on adopte la convention, pour chaque nœud interne, que la plus grande des étiquettes du sous-arbre droit est supérieure aux étiquettes du sous-arbre gauche.
Ainsi, l'arbre 1 de la figure 3 est représenté par :
Un arbre non raciné à
Enfin, pour assurer l'unicité de la représentation informatique d'un arbre, et ainsi simplifier les programmes, on adopte la convention, pour chaque nœud interne, que la plus grande des étiquettes du sous-arbre droit est supérieure aux étiquettes du sous-arbre gauche.
Ainsi, l'arbre 1 de la figure 3 est représenté par :
Noeud (Noeud (Feuille 3,
Noeud (Noeud (Feuille 1,
Feuille 2),
Feuille 4)),
5);;
On représente les graphes par liste d'adjacence, plus précisément par une liste de couples dont le premier élément est le nom d'un sommet et le second la liste d'adjacence de ce sommet.
type graphe
Q 41. Écrire une fonction feuilles qui prend en argument un arbre et renvoie la liste des étiquettes de ses feuilles.
Q 42. Écrire une fonction degres qui prend en argument un graphe implémenté par liste d'adjacence et renvoie la liste des degrés de ces nœuds.
Q 43. Écrire une fonction egaux qui teste si deux arbres sont égaux, au sens des arbres binaires non racinés étiquetés. Justifier que cette fonction est correcte.
Q 44. Étant donnés une liste d'arbres et un arbre, écrire une fonction appartient qui teste si l'arbre fait partie de la liste.
Q 45. En remarquant que parmi les 4 sous-arbres à échanger pour un mouvement de NNI autour d'une branche interne, on peut en choisir un qui restera fixe, écrire une fonction voisinsNNI qui prend en argument un arbre et renvoie tous les arbres que l'on peut obtenir à partir de celui-ci par un mouvement NNI.
Q 46. Écrire une fonction chenille qui prend en argument un entier
Q 47. Écrire une fonction insere qui prend en arguments un arbre et un graphe et ajoute l'arbre à la liste des sommets du graphe.
Q 48. Écrire une fonction relie qui prend en arguments un graphe et deux arbres et qui rajoute au graphe une arête reliant les deux sommets, si elle n'est pas déjà présente.
Q 49. Écrire une fonction grapheNNI qui prend en argument un entier
type graphe
Q 41. Écrire une fonction feuilles qui prend en argument un arbre et renvoie la liste des étiquettes de ses feuilles.
Q 42. Écrire une fonction degres qui prend en argument un graphe implémenté par liste d'adjacence et renvoie la liste des degrés de ces nœuds.
Q 43. Écrire une fonction egaux qui teste si deux arbres sont égaux, au sens des arbres binaires non racinés étiquetés. Justifier que cette fonction est correcte.
Q 44. Étant donnés une liste d'arbres et un arbre, écrire une fonction appartient qui teste si l'arbre fait partie de la liste.
Q 45. En remarquant que parmi les 4 sous-arbres à échanger pour un mouvement de NNI autour d'une branche interne, on peut en choisir un qui restera fixe, écrire une fonction voisinsNNI qui prend en argument un arbre et renvoie tous les arbres que l'on peut obtenir à partir de celui-ci par un mouvement NNI.
Q 46. Écrire une fonction chenille qui prend en argument un entier
Q 47. Écrire une fonction insere qui prend en arguments un arbre et un graphe et ajoute l'arbre à la liste des sommets du graphe.
Q 48. Écrire une fonction relie qui prend en arguments un graphe et deux arbres et qui rajoute au graphe une arête reliant les deux sommets, si elle n'est pas déjà présente.
Q 49. Écrire une fonction grapheNNI qui prend en argument un entier
II.D
On va démontrer par récurrence que
On note
Q 50. Montrer que les sous-graphes
Q 51. Soient
Q 52. Démontrer par récurrence que
On note
Q 50. Montrer que les sous-graphes
Q 51. Soient
Q 52. Démontrer par récurrence que
