Ce sujet s'intéresse à la modélisation de voitures de courses évoluant sur un circuit.
Les deux premières parties consistent à représenter un circuit suivant deux modélisations différentes, à vérifier la cohérence de sa représentation puis à le tracer à l'écran. La troisième partie évalue, en fonction des caractéristiques du circuit, le temps idéal pour effectuer un tour puis une course entière. La dernière partie est dédiée à la gestion des résultats du championnat de formule 1 et à la réalisation de statistiques sur plusieurs années.
Le championnat du monde de formule 1 a été créé en 1950. Chaque année, une vingtaine de courses (appelées grand prix), auxquelles prennent part une vingtaine de pilotes, se courent sur différents circuits et comptent pour ce championnat. Ces nombres ont cependant légèrement varié depuis sa création. Les courses proprement dites sont précédées de séances de «qualifications » qui permettent, en particulier, de définir l'ordre des voitures sur la grille de départ. Chaque course fait environ 300 km , ce qui représente entre 40 et 80 tours de circuit suivant la longueur de celui-ci.

Les seuls langages de programmation autorisés dans cette épreuve sont Python et SQL. Pour répondre à une question, il est possible de faire appel aux fonctions définies dans les questions précédentes. Dans tout le sujet on suppose que les bibliothèques math, numpy et turtle sont rendues accessibles grâce à l'instruction
import math, numpy as np, turtle
Si les candidats font appel à des fonctions d'autres bibliothèques, ils doivent préciser les instructions d'importation correspondantes.
Ce sujet utilise la syntaxe des annotations pour préciser le type des paramètres et du résultat des fonctions à écrire. Ainsi
def maFonction(n:int, X:[float], c:str, u) -> (int, np.ndarray):
signifie que la fonction maFonction prend quatre paramètres, le premier ( n ) est un entier, le deuxième ( X ) une liste de nombres à virgule flottante, le troisième (c) une chaine de caractères et le type du dernier (u) n'est pas précisé. Cette fonction renvoie un couple dont le premier élément est un entier et le deuxième un tableau numpy. Il n'est pas demandé aux candidats de recopier les entêtes avec annotations telles qu'elles sont fournies dans ce sujet, ils peuvent utiliser des entêtes classiques. Ils veilleront cependant à décrire précisément le rôle des fonctions qu'ils définiraient eux-mêmes.
Les candidats peuvent à tout moment supposer qu'une fonction définie dans une question précédente est disponible, même s'ils n'ont pas traité la question correspondante. Pour les questions de programmation, cela revient à disposer d'une fonction respectant exactement la spécification de l'énoncé, sans propriété supplémentaire.
Dans ce sujet, le terme «liste» appliqué à un objet Python signifie qu'il s'agit d'une variable de type list. Les termes «vecteur» et «tableau» désignent des objets numpy de type np.ndarray, respectivement à une dimension ou de dimension quelconque. Enfin le terme «séquence» représente une suite itérable et indiçable, indépendamment de son type Python, ainsi un tuple d'entiers, une liste d'entiers et un vecteur d'entiers sont tous trois des «séquences d'entiers».
Une attention particulière sera portée à la lisibilité, la simplicité et l'efficacité du code proposé. En particulier, l'utilisation d'identifiants significatifs, l'emploi judicieux de commentaires et la description du principe de chaque programme seront appréciés.
Une liste de fonctions utiles est fournie à la fin du sujet.

I Modélisation sommaire d'un circuit

Dans un premier temps, nous considérons un circuit constitué uniquement de segments de droite et de virages à angle droit. Un tel circuit est représenté par une liste de chaines de caractères dont les éléments sont "A", "G" et "D" où

"A" représente une portion de ligne droite de longueur déterminée,
"G" correspond à un virage à à gauche et
"D" à un virage à à droite.

La figure 1 donne un exemple de circuit et de sa représentation.

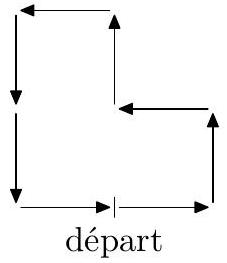
Figure 1 Circuit correspondant à la liste

["A", "G", "A", "G", "A", "D", "A", "G", "A", "G", "A", "A", "G", "A"]

I.A - Validité de la représentation d'un circuit

Q 1. Écrire une fonction d'entête

def longueur1(c:[str], d:int) -> int:

qui prend en paramètres c , une liste représentant un circuit, et d la longueur, en mètres, des portions de ligne droite utilisées et renvoie la longueur totale du circuit en mètres.
Q 2. Donner la valeur de l'expression représentation_minimale(["A", "A", "G", "D", "G", "G", "G", " A "

) où représentation_minimale est la fonction définie en figure 2. Que représente la variable nbg ?

def représentation_minimale(c:[str]) -> [str]:
    virages = [[], ["G"], ["G", "G"], ["D"]]
    nbg = 0
    res = []
    for e in c:
        if e == "A":
            res.extend(virages[nbg])
            nbg = 0
            res.append("A")
        elif e == "G":
            nbg = (nbg + 1) % 4
        else:
            nbg = (nbg - 1) % 4
    res.extend(virages[nbg])
    return res

Figure 2

Q 3. Expliquer en quelques lignes le but de la fonction représentation_minimale.
Q 4. Toutes les voitures sur un circuit automobile roulent dans le même sens. Ainsi, un demi-tour (deux virages à droite ou deux virages à gauche) n'est pas envisageable. Écrire une fonction d'entête
def contient_demi_tour1(c:[str]) -> bool:
qui prend en paramètre une représentation d'un circuit et renvoie True si le circuit c comporte un demi-tour et False s'il n'en contient pas.
Q 5. Écrire une fonction d'entête
def est_fermé1(c:[str]) -> bool:
qui détermine si le circuit c est fermé, autrement dit, si une voiture qui le parcourt revient à la fin du circuit à son point de départ dans la même orientation qu'au début.
Q 6. Il faut éviter qu'une partie de la trajectoire en croise ou se superpose à une autre, même en imaginant un tunnel ou un pont, cela rendrait la sécurité des pilotes très difficile à assurer. Écrire une fonction d'entête
def circuit_convenable1(c:[str]) -> bool:
qui détermine si le circuit c, fourni dans une représentation de longueur minimale, respecte les critères attendus : il est fermé et ne comporte pas de demi-tour, ni de sections qui se superposent ou se croisent. On pourra remarquer, en le justifiant, que, dans la modélisation utilisée, les croisements éventuels ont forcément lieu à une extrémité d'un élément de ligne droite.

I.B - Tracé d'un circuit

Q 7. En utilisant la bibliothèque turtle, dont une description figure en fin de sujet, écrire une fonction d'entête

def dessine_circuit1(c:[str], d:int) -> None:

qui prend en paramètre la représentation d'un circuit convenable et la longueur, en pixels, d'un segment de ligne droite et dessine le circuit correspondant à l'écran.

II Modélisation plus réaliste d'un circuit

Afin de représenter un circuit de manière plus réaliste, la modélisation précédente est enrichie en considérant que les virages sont des arcs de cercle. Un virage est désormais modélisé par un tuple de deux entiers (

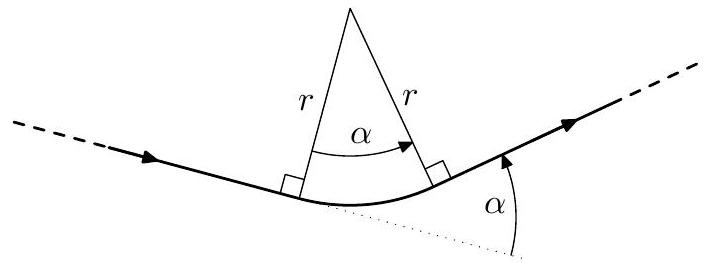
) dans lequel le premier élément désigne le rayon du virage en mètres (entier strictement positif) et le second son angle en degrés (dans l'intervalle ]-360, 360 [). L'angle est orienté dans le sens trigonométrique, un angle positif désigne un virage à gauche et un angle négatif un virage à droite (figure 3). De plus, une ligne droite est désormais représentée par un entier correspondant à sa longueur en mètres (entier strictement positif). Un exemple de circuit de ce type est donné figure 4.

Figure 3 Représentation d'un virage

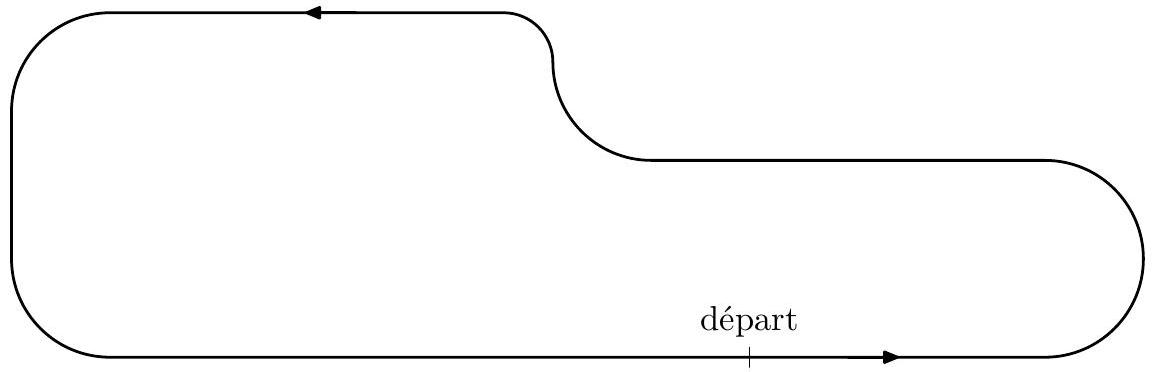
Figure 4 Circuit correspondant à la liste

Dans toute la suite du sujet, nous utiliserons cette nouvelle modélisation pour représenter un circuit. Cette modélisation reste toutefois imparfaite. Dans la réalité, les virages ne sont pas des arcs de cercle, leur rayon de courbure varie tout au long du virage. De plus un circuit n'est pas forcément plan et certains circuits proposent des virages relevés qui autorisent des vitesses plus élevées.

II.A - Validation

Q 8. Écrire une fonction d'entête
def élément_valide2(e) -> bool:
qui prend en paramètre un objet quelconque et détermine s'il peut figurer dans une liste représentant un circuit, autrement dit s'il s'agit d'un entier strictement positif ou d'un tuple de deux entiers de valeurs compatibles avec les spécifications de la modélisation.
Dans toute la suite du sujet, on considère que les représentations des circuits utilisées respectent la forme attendue.

II.B - Première méthode de tracé à l'écran

Q 9. En utilisant le module turtle, écrire une fonction d'entête
def dessine_circuit2(c:list, échelle:float) -> None:
qui trace à l'écran le circuit représenté par la liste c à l'échelle échelle exprimée en pixels par mètre.

II.C - Tracé pixel par pixel

Dans cette sous-partie, on réalise le tracé d'un circuit sous forme matricielle, pixel par pixel.
On représente l'écran par un tableau d'entiers à deux dimensions. Chaque élément du tableau représente un pixel, 0 désigne un pixel noir et 1 un pixel blanc. L'élément d'indice ( 0,0 ) correspond au pixel situé en bas à gauche. Le premier indice correspond à la colonne du pixel, le second à sa ligne.
On dispose des deux fonctions d'entête
def ligne(s:np.ndarray, début:np.ndarray, fin:np.ndarray) -> None:
def arc(s:np.ndarray, début:np.ndarray, centre:np.ndarray, angle:int) -> None:
qui prennent en paramètre un tableau à deux dimensions

représentant l'écran et le modifient pour tracer, en noir, respectivement une ligne droite entre les pixels dont les cordonnées (colonne, ligne) sont données par les vecteurs début et fin et un arc de cercle d'angle angle degrés, commençant au pixel début et dont le centre est situé au point de coordonnées centre dans le système de coordonnées de l'écran d'unité un pixel. Si l'angle est
positif, l'arc est tracé dans le sens trigonométrique, sinon, il est tracé dans le sens horaire. Si les tracés demandés sortent de l'écran, seules les parties visibles sont dessinées sans produire d'erreur.
Q 10. Écrire une fonction d'entête

def matrot(t:int) -> np.ndarray:

qui prend en paramètre un angle exprimé en degrés et renvoie un tableau numpy correspondant à la matrice de la rotation plane de centre

et d'angle

.
Q 11. La figure 5 présente un extrait de programme Python. En s'appuyant sur la figure 3, préciser la signification et la nature des paramètres de la fonction cc et de son résultat. Un schéma explicitant le principe de la fonction sera apprécié.

def signe(x):
    if x > 0: return 1
    elif x < 0: return -1
    return 0
def cc(pos, dir, r, alpha):
    return pos + matrot(dir) © np.array([0., signe(alpha) * r])

Figure 5 Extrait de programme

Q 12. Écrire une fonction d'entête
def dessine_circuit3(s:np.ndarray, c:list, échelle:float) -> None:
qui prend en paramètres un tableau s représentant l'écran de l'ordinateur et le modifie pour tracer, en partant du centre de l'écran, le circuit représenté par la liste c à raison de échelle pixels par mètre.

III Le parcours d'une voiture

Cette partie s'intéresse au parcours par une voiture de course d'un circuit, tel qu'il a été modélisé dans la partie précédente. La voiture considérée est capable d'une accélération maximale notée

, d'un freinage maximal (accélération négative) noté

et d'une vitesse maximale

. Nous supposons que la voiture peut produire son accélération maximale et son freinage maximal instantanément et les maintenir de manière continue tant que sa vitesse reste dans l'intervalle [

].
Dans le modèle utilisé où les virages sont des arcs de cercle, le rayon du virage détermine une vitesse recommandée pour prendre ce virage. Par ailleurs, indépendamment de la vitesse d'entrée dans un virage, on suppose que les virages sont toujours parcourus à vitesse constante.
Pour toutes les applications numériques, on prendra les valeurs

III.A - Formules de calcul des vitesses et temps de parcours

III.A.1)

Q 13. La voiture est à l'arrêt au début d'une ligne droite. Le pilote démarre et accélère au maximum, exprimer le temps nécessaire pour atteindre la vitesse maximale. Faire l'application numérique.
Q 14. Exprimer le temps minimal nécessaire à une voiture qui roule en ligne droite à la vitesse

pour passer à la vitesse

. Distinguer les cas

. Faire l'application numérique pour

.
Q 15. Montrer que la distance minimale nécessaire à une voiture qui roule en ligne droite à la vitesse

pour passer à la vitesse

s'écrit

Q 16. Exprimer la distance minimale nécessaire à une voiture qui roule en ligne droite à la vitesse

pour passer à la vitesse

. Faire l'application numérique pour

III.A.2)

On s'intéresse maintenant au temps de parcours d'une ligne droite de longueur

entre un virage d'où l'on sort à la vitesse

et un virage qu'on doit prendre à la vitesse

. Afin de parcourir la ligne droite le plus rapidement possible, le pilote accélère au maximum jusqu'au moment où il lui faut freiner pour arriver à l'entrée du virage à la vitesse

.
Q 17. Exprimer

, la longueur minimale de la ligne droite pour que la vitesse

soit atteinte.
Q 18. Si la longueur de la ligne droite est supérieure au seuil calculé à la question précédente (

), exprimer le temps minimal nécessaire pour parcourir la ligne droite.

, on note alors

la vitesse maximale atteinte dans la ligne droite. On ne demande pas de calculer cette vitesse.
Q 19. Exprimer, en fonction de

et des autres données du problème, le temps minimal nécessaire pour traverser une telle ligne droite.

III.B - Implantation en Python

Les instructions suivantes sont exécutées au début du programme Python, ainsi toutes les fonctions ont accès aux trois constantes AMAX, FMAX et VMAX correspondant respectivement aux valeurs maximales de l'accélération, du freinage et de la vitesse de la voiture considérée.

AMAX = 10 # accélération maximale en m/s}\mp@subsup{}{}{2
FMAX = -20 # freinage maximal en m/s }\mp@subsup{}{}{2
VMAX = 100 # vitesse maximale en m/s

On dispose par ailleurs des fonctions d'entête

def vr(r:int) -> float:
def vmax_droite(d:int, v1:float, v2:float) -> float:

La fonction vr calcule la vitesse recommandée, en mètres par seconde, pour un virage de rayon r exprimé en mètres. La fonction vmax_droite détermine la vitesse maximale, en mètres par seconde, que l'on peut atteindre sur une ligne droite de longueur d (exprimée en mètres) dans laquelle on entre à la vitesse v1 et dont on sort à la vitesse v2 (exprimées en mètres par seconde) ; le résultat de cette fonction est toujours inférieur ou égal à la valeur de VMAX. Ces deux fonction s'exécutent en temps constant.

III.B.1) Temps pour un tour

Pour un circuit donné, on cherche d'abord à déterminer la vitesse maximale possible à l'entrée de chaque virage. Cette vitesse peut être inférieure à la vitesse recommandée pour un virage car il faut tenir compte d'un éventuel virage ultérieur plus serré, sans ligne droite de longueur suffisante pour freiner. Dans ce cas, il faut réduire la vitesse en amont afin de ne pas dépasser la vitesse recommandée dans le virage serré.
Q 20. Écrire une fonction d'entête

def vitesses_entrée_max(c:list, vf:float) -> [float]:

qui prend en paramètre la représentation d'un circuit et la vitesse maximale (en mètres par seconde) à respecter à la fin du circuit et qui calcule, pour chacun de ses éléments (lignes droites et virages), la vitesse maximale à l'entrée de l'élément de façon à ne jamais dépasser la vitesse recommandée dans les virages qui suivent ni la vitesse vf en fin de circuit.
Q 21. Écrire une fonction d'entête

def temps_droite(d:int, v1:float, v2:float) -> (float, float):

qui prend en paramètre la longueur d'une ligne droite, la vitesse de la voiture à l'entrée de cette ligne droite et la vitesse maximale souhaitée à sa sortie et qui calcule le temps minimal nécessaire pour parcourir cette ligne droite et la vitesse effectivement atteinte à l'extrémité de la ligne droite. S'il n'est pas possible de sortir de la ligne droite avec une vitesse inférieure ou égale à v2, cette fonction lève l'exception ValueError.
Q 22. Écrire une fonction d'entête

def temps_tour(c:list, v0:float, vf:float) -> float:

qui prend en paramètre un circuit, la vitesse à l'entrée du circuit et la vitesse maximale autorisée à la fin du tour et qui calcule le temps minimal, en secondes, pour effectuer un tour de ce circuit, sans jamais dépasser la vitesse recommandée de chaque virage ni la vitesse finale maximale passée en paramètre.

III.B.2) Temps de course

Un grand prix de formule 1 est une course d'environ 300 km , ce qui représente entre 40 et 80 tours de circuit suivant la longueur de celui-ci. Au moment du départ les voitures sont à l'arrêt sur la grille de départ. Comme les tours de circuit s'enchainent, il convient d'anticiper à la fin d'un tour la vitesse pour débuter le tour suivant, afin d'être sûr de ne pas dépasser la vitesse d'entrée maximale du premier virage. Cependant, à la fin du dernier tour, les pilotes n'ont pas à négocier de prochain virage et disposent après la ligne d'arrivée d'un dégagement suffisant pour ralentir quelle que soit leur vitesse. La vitesse à la fin du dernier tour n'est donc pas limitée.
Q 23. Écrire une fonction d'entête

def temps_course(c:list, n:int) -> float:

qui calcule le temps minimal (en secondes) nécessaire pour effectuer une course de n tours du circuit c sans jamais dépasser la vitesse recommandée de chaque virage. Le départ est donné à l'arrêt, les lignes de départ et d'arrivée sont confondues et la vitesse sur la ligne d'arrivée à l'issue du dernier tour n'est pas limitée.
Q 24. Déterminer la complexité temporelle asymptotique dans le pire des cas de la fonction temps_course en fonction de n et du nombre de segments du circuit c (longueur de la liste).

IV Gestion des résultats

Depuis la création du championnat du monde de formule 1 en 1950, la fédération internationale de l'automobile (FIA) conserve l'ensemble des résultats des différents grands prix. Ces différentes informations sont stockées dans une base de données relationnelle dont un modèle physique simplifié est schématisé figure 6 .

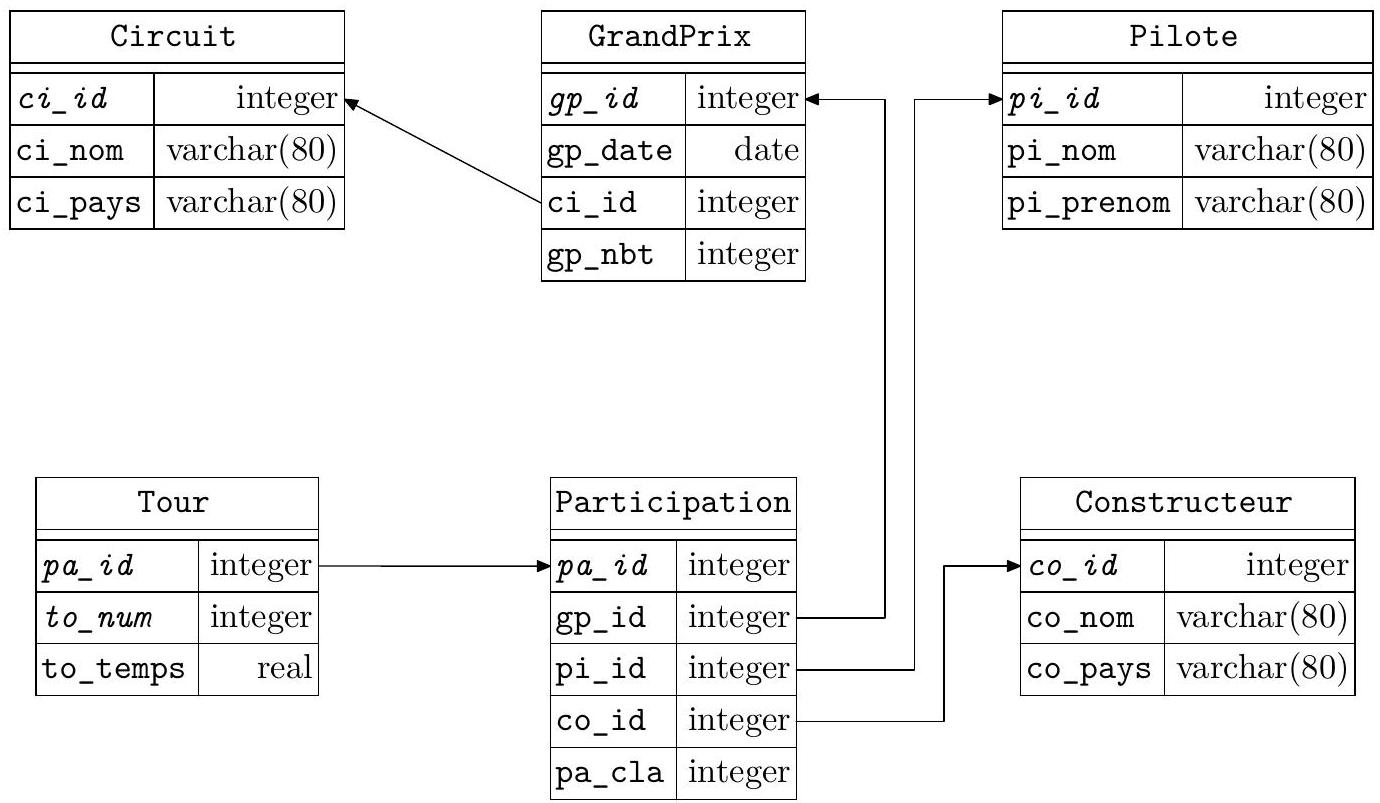
Figure 6 Structure physique simplifiée de la base de données du championnat du monde de formule 1

Cette base comporte les six tables listées ci-dessous avec la description de leurs colonnes:

la table Circuit de circuits utilisés pour le championnat du monde de formule 1
ci_id identifiant (entier arbitraire) du circuit (clef primaire)
ci_nom nom du circuit (généralement le nom de la ville ou de la région dans laquelle il se trouve)
ci_pays pays dans lequel se trouve le circuit
la table GrandPrix des courses comptant pour le championnat du monde
gp_id identifiant (entier arbitraire) du grand prix (clef primaire)
gp_date date de la course
ci_id circuit sur lequel s'est déroulé la course
gp_nbt nombre de tours de circuit
la table Pilote des pilotes de formule 1
pi_id identifiant (entier arbitraire) du pilote (clef primaire)
pi_nom nom de famille du pilote
pi_prenom prénom du pilote
la table Constructeur des écuries de formule 1
co_id identifiant (entier arbitraire) de l'écurie (clef primaire)
co_nom nom de l'écurie
co_pays pays d'origine de l'écurie
la table Participation des participants (couple pilote, constructeur) pour une course donnée
pa_id identifiant (entier arbitraire) de la participation (clef primaire)
gp_id la course
pi_id le pilote
co_id le constructeur
pa_cla le classement à l'arrivée de ce participant ou NULL s'il n'a pas terminé la course ou a été disqualifié
la table Tour des temps mis par un participant pour chaque tour de course, de clef primaire (pa_id, to_num)
pa_id identifiant (entier arbitraire) de la participation
to_num numéro du tour (de 1 à gp_nbt)
to_temps le temps (en secondes) pour le tour correspondant

Q 25. Pourquoi avoir utilisé la colonne pi_id comme clef primaire de la table pilote et pas la colonne pi_nom?
Q 26. Estimer le nombre de lignes de la table Tour.

Q 27. Écrire une requête SQL qui liste, par ordre chronologique, la date et le nom du circuit de toutes les courses qui se sont déroulées en France (ci_pays = 'France').
Q 28. Écrire une requête SQL qui liste, pour chaque course de l'année 2021, le nom du circuit, le nom du pilote gagnant et son temps de course.
Q 29. Expliquer le résultat de la requête suivante

SELECT ci_nom, pi_nom, gp_date, to_temps
FROM (SELECT ci_id, ci_nom, MIN(to_temps) AS mtt
        FROM Circuit
            JOIN GrandPrix ON GrandPrix.ci_id = Circuit.ci_id
            JOIN Participation ON Participation.gp_id = GrandPrix.gp_id
            JOIN Tour ON Tour.pa_id = Participation.pa_id
        GROUP BY
            ci_id, ci_nom
        ) AS rdc
    JOIN GrandPrix ON GrandPrix.ci_id = rdc.ci_id
    JOIN Participation ON Participation.gp_id = GrandPrix.gp_id
    JOIN Pilote ON Pilote.pi_id = Participation.pi_id
    JOIN Tour ON Tour.pa_id = Participation.pa_id AND to_tmps = mtt
ORDER BY
    ci_nom

Opérations et fonctions disponibles

Fonctions

a % b calcule le reste de la division euclidienne de a par b, son signe est toujours celui de b .
isinstance ( ) teste si l'objet o est de type t isinstance(-13, int) True, isinstance( , tuple) True.
range( int) renvoie la séquence des n premiers entiers ( ) list(range(5)) .
range(d:int, f:int, s:int) construit une séquence d'entiers espacés de s débutant à d et finissant avant f list (range ) .
enumerate(s) itère sur la séquence en renvoyant, pour chaque élément de , un couple formé de son indice et de l'élément considéré
list (enumerate .
renvoie son plus petit (respectivement plus grand) argument
.
math.sqrt(x) calcule la racine carrée du nombre x.
round(n) arrondit le nombre n à l'entier le plus proche.
math.pi valeur approchée de la constante .

Opérations sur les listes

len(u) donne le nombre d'éléments de la liste u
, len .
u.count(e) renvoie le nombre d'éléments de la liste u égaux à e
.count .
construit une liste constituée de la concaténation des listes u et v
.
construit une liste constituée de la liste u concaténée fois avec elle-même
.
remplace l'élément d'indice i de la liste u par e.
remplace les éléments de la liste dont les indices sont compris dans l'intervalle par ceux de la séquence v (peut modifier la longueur de la liste u ).
u.append(e) ajoute l'élément e à la fin de la liste u (identique à u[len(u):] = [e]). On suppose que cette opération a une complexité temporelle en .
u.extend(v) ajoute les éléments de la séquence à la fin de la liste (identique à . On suppose que cette opération a une complexité temporelle en .
u.insert(i, e) insère l'élément e à la position d'indice i dans la liste u (en décalant les éléments suivants) ; si i , e est ajouté en fin de liste (identique à u[i:i] = [e]).
del u[i] supprime de la liste u son élément d'indice i (identique à u[i:i+1] = []).
del supprime de la liste tous ses éléments dont les indices sont compris dans l'intervalle (identique à ).
u.reverse() modifie la liste u en inversant l'ordre de ses éléments. On suppose que cette opération a une complexité temporelle en .
e in teste si l'élément e apparait dans la liste .

Opérations sur les tableaux

np.array(s) crée un nouveau tableau contenant les éléments de la séquence . La forme de ce tableau est déduite du contenu de
np.array .
a.ndim nombre de dimensions du tableau a.
a.shape tuple donnant la taille du tableau a pour chacune de ses dimensions.
a.size nombre total d'éléments du tableau a.
np.around(a) produit un tableau dont les éléments sont ceux du tableau a arrondis à l'entier le plus proche.
@ calcule le produit matriciel des deux tableaux et . Les dimensions de et doivent être compatibles. On suppose que la multiplication d'une matrice et d'un vecteur a une complexité temporelle en .

Module graphique turtle

Le module turtle, inspiré du langage Logo, simule une «tortue» robot qui se déplace sur l'écran. Cette tortue est munie d'un «crayon» qui, quand il est baissé, trace à l'écran la trajectoire de la tortue. Au début du programme, la tortue est située au centre de la fenêtre de visualisation, crayon baissé et orientée vers la droite de l'écran.

turtle.pendown(), turtle.penup() baisse ou lève le crayon.
turtle.right(a), turtle.left(a) fait pivoter la tortue sur place à droite ou à gauche de a degrés.
turtle.forward(n), turtle.back(n) fait avancer ou reculer la tortue de pixels (si est négatif, le mouvement est inversé) ; n peut être un entier ou un nombre à virgule flottante.
turtle. circle(r, a) fait parcourir par la tortue un arc de cercle de a degrés dont le centre est situé pixels à gauche de la tortue. Si r est positif, le centre est effectivement à gauche de la tortue et l'arc de cercle est parcouru dans le sens trigonométrique ; si r est négatif, le centre est situé à droite de la tortue et l'arc de cercle est parcouru dans le sens horaire. Si a est positif, l'arc de cercle est parcouru en marche avant, la tortue tourne donc à gauche si est positif et à droite si est négatif. Si a est négatif, l'arc de cercle est parcouru en marche arrière, la tortue recule sur sa gauche si est positif et sur sa droite si est négatif.
turtle.home() ramène la tortue au centre de la fenêtre, orientée vers la droite de l'écran.
turtle.reset() efface la fenêtre et repositionne la tortue au centre, orientée vers la droite de l'écran.

Fonctions SQL

COUNT (*) fonction agrégative qui retourne le nombre de lignes chaque groupe.
COUNT(e) fonction agrégative qui calcule le nombre de valeurs non nulles chaque groupe de lignes.
MIN(e), MAX(e) fonctions agrégatives qui calculent respectivement le minimum et le maximum de e pour chaque groupe de lignes ; e est une expression de type numérique, chaine de caractère ou date, heure.
SUM(e) fonction agrégative qui somme e pour chaque groupe de lignes ; e est une expression de type numérique ou durée.
EXTRACT (c FROM d) extrait la composante c de la date d , d peut être n'importe quelle expression de type date, timestamp, time ou interval et c peut prendre une des valeurs (liste non exhaustive) 'century', 'year', 'quarter' (trimestre, 1 à 4), 'month' (mois, 1 à 12), 'day' (jour du mois, 1 à 31), 'dow' (jour de la semaine, 0 à 6,0 désignant dimanche), 'doy' (jour de l'année, 1 à 366 ).