Une photomosaïque (figure 1) est une image composée à la manière d'une mosaïque, où les fragments sont euxmêmes des petites images, appelées vignettes. Elle est créée à partir d'une image appelée image source. Chaque vignette remplace une zone de même forme dans l'image source appelée pavé. Les vignettes sont fabriquées à partir d'une collection d'images appelée banque d'images.
L'intérêt est essentiellement artistique: vue de loin, une photomosaïque ressemble à l'image source; en se rapprochant, on reconnait les vignettes.

Figure 1 Photomosaïque d'un surfer composée de 1600 vignettes - de gauche à droite : l'image source

, la photomosaïque et 16 vignettes

(détail du pied)

De nombreux paramètres régissent la construction d'une photomosaïque et la qualité du résultat :

la structure du pavage utilisé (nombre, forme et arrangement des vignettes);
le nombre et la diversité des images de la banque ;
les algorithmes mis en œuvre pour:
sélectionner les bonnes images dans la banque (partie III);
redimensionner les images (partie II) ;
placer les vignettes (partie IV).

Dans la suite du sujet, les photomosaïques sont construites sur des pavages rectangulaires réguliers, c'est-à-dire, constitués de vignettes rectangulaires, toutes de mêmes dimensions et juxtaposées bord à bord.

Les seuls langages de programmation autorisés dans cette épreuve sont Python et SQL. Pour répondre à une question, il est possible de faire appel aux fonctions définies dans les questions précédentes. Dans tout le sujet, on suppose que les modules math, numpy, matplotlib.pyplot et random ont été rendus accessibles grâce à l'instruction
import math, numpy as np, matplotlib.pyplot as plt, random
Si les candidats font appel à des fonctions d'autres bibliothèques, ils doivent préciser les instructions d'importation correspondantes.

Dans tout le sujet, le terme «liste» appliqué à un objet Python signifie qu'il s'agit d'une variable de type list. Les termes «vecteur» et «tableau» désignent des objets numpy de type np.ndarray, respectivement à une dimension ou de dimension quelconque. Enfin le terme «séquence» représente une suite itérable et indiçable, indépendamment de son type Python, ainsi un tuple d'entiers, une liste d'entiers et un vecteur d'entiers sont tous trois des «séquences d'entiers ».

Les entêtes des fonctions demandées sont annotés pour préciser les types des paramètres et du résultat. Ainsi, def uneFonction(n:int, X:[float], c:str, u) -> np.ndarray:
signifie que la fonction uneFonction prend quatre paramètres

, où

est un entier,

une liste de nombres à virgule flottante, c une chaine de caractères et le type de u n'est pas précisé. Cette fonction renvoie un tableau numpy.
Il n'est pas demandé aux candidats d'annoter leurs fonctions, la rédaction pourra commencer par
def uneFonction(

):
De façon générale, une attention particulière sera portée à la lisibilité, la simplicité et la clarté du code proposé. L'utilisation d'identifiants significatifs, l'emploi judicieux de commentaires seront appréciés.
Une liste de fonctions potentiellement utiles est fournie à la fin du sujet.

I Pixels et images

I.A - Pixels

Un pixel (contraction de l'anglais picture element) est un élément de couleur homogène utilisé pour représenter une image sous forme numérique. La teinte d'un pixel peut être représentée de plusieurs façons. Une méthode courante, basée sur la synthèse additive, consiste à la décomposer en trois composantes qui correspondent aux couleurs rouge, vert et bleu. On parle de représentation RGB (pour red, green et blue). Chacune des trois composantes donne l'intensité de la couleur correspondante dans la teinte finale, 0 indiquant l'absence de cette couleur. Ainsi, le triplet (

) désigne un pixel noir.
Q 1. On suppose que chacune des trois composantes RGB d'un pixel est représentée par un nombre entier positif ou nul, codé sur 8 bits. Combien de couleurs différentes peut-on représenter avec un tel pixel?
Dans la suite, on représente un pixel par un vecteur (tableau numpy à une dimension) d'entiers de type np.uint8 (entier non signé codé sur 8 bits) à trois éléments, correspondant respectivement à chacune des composantes RGB du pixel ; on utilise dans toute la suite le type pixel pour désigner un tel vecteur.
Q 2. Donner une instruction permettant de créer un vecteur correspondant à un pixel blanc.
Il est rappelé qu'en Python, comme dans beaucoup de langages de programmation, les opérations d'addition, soustraction, multiplication, division entière, modulo et élévation à la puissance (opérateurs

) appliquées à deux opérandes de même type fournissent un résultat du type de leurs opérandes. Cela peut conduire à un dépassement de capacité et à une erreur de calcul car, les dépassements de capacité étant par défaut «silencieux», ils ne produisent pas d'erreur lors de l'exécution du programme.
L'opérateur division (/) entre deux entiers produit toujours un résultat sous forme de nombre à virgule flottante même si la division est exacte (

). Il en est de même pour toute fonction faisant implicitement appel à cet opérateur comme np.mean.
Q 3. On pose

. uint8(280) et

. uint8(240). Que valent

?
Les fonctions numpy qui effectuent de manière répétitive des opérations élémentaires, si elles ne garantissent pas l'absence de dépassement de capacité, prennent la précaution d'utiliser pour leurs calculs intermédiaires et leur résultat un type compatible avec le type de base de la plus grande capacité possible. Par exemple le résultat de np.sum(np.array([100, 200], np.uint8)) est de type np.uint64 (entier non signé codé sur 64 bits) et vaut bien 300.
Pour représenter une image en niveau de gris, on peut se contenter d'une valeur par pixel, représentant l'intensité du gris entre le noir et le blanc. Pour convertir une image en couleurs en niveaux de gris, on peut remplacer chaque pixel par un seul entier, dont la valeur correspond à la meilleure approximation entière de la moyenne des trois composantes RGB du pixel.
Q 4. Écrire une fonction d'entête
def gris(p:pixel) -> np.uint8:
qui calcule le niveau de gris correspondant au pixel p.

I.B - Images

Une image en niveaux de gris de taille

(

pixels de large,

pixels de haut) est associée à un tableau d'octets (type np.uint8) à deux dimensions, à

lignes et

colonnes. Chaque élément de ce tableau représente le niveau de gris du pixel correspondant. Ainsi le tableau à deux dimensions img1, défini par :

img1 = np.array([[ 85, 0, 127, 170, 85, 150],
    [119, 102, 102, 123, 81, 170],
    [255, 170, 90, 112, 63, 97],
    [171, 212, 225, 186, 162, 171]], np.uint8)

définit une image de taille

, représentée figure 2 .
Dans toute la suite, on utilise le type image pour désigner un tableau d'octets à deux dimensions.

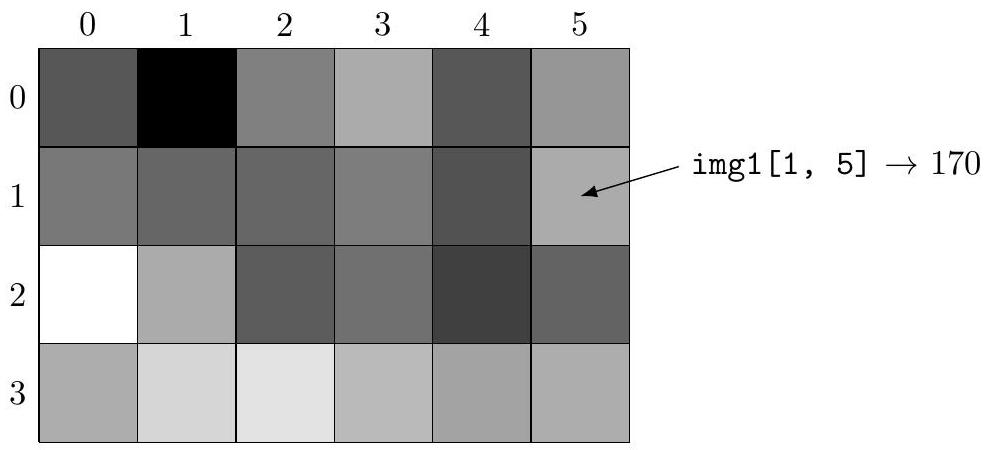
Figure 2 Visualisation de l'image img1

Pour les images en couleurs, on ajoute une dimension pour représenter les trois composantes d'un pixel. L'instruction source = plt.imread("surfer.jpg") charge dans un tableau numpy l'image en couleurs contenue dans le fichier surfer.jpg. Les expressions source.shape et source [ 0,0 ] valent alors respectivement :

Q 5. Interpréter ces valeurs.
Q 6. Écrire une fonction d'entête
def conversion(a:np.ndarray) -> image:
qui qénère une image en niveaux de gris correspondant à la conversion de l'image en couleurs a.

II Redimensionnement d'images

On s'intéresse dans cette partie à plusieurs algorithmes de redimensionnement d'une image A, de taille

(

pixels de large par

pixels de haut, on note

son nombre total de pixels), en une image a de taille

(on pose

). Nous nous intéresserons dans la suite uniquement à des images en niveau de gris.

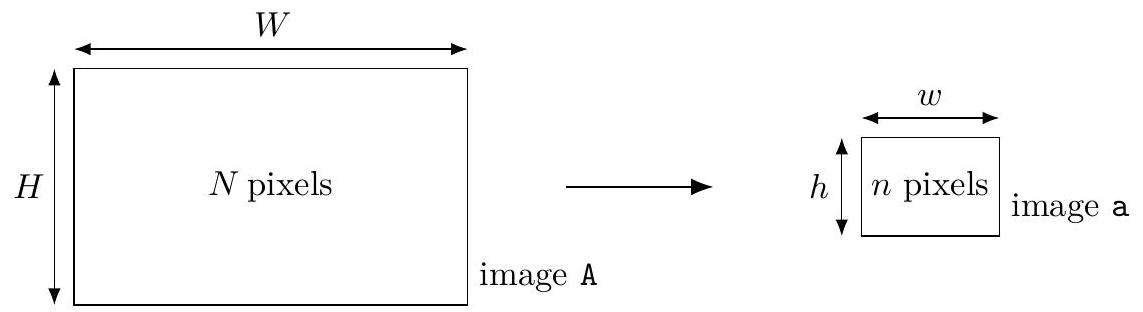
Figure 3 Redimensionnement d'image

II.A - Le contexte

À l'occasion du mariage d'Alice et de Bernard, leurs amis souhaitent réaliser plusieurs photomosaïques sur des thèmes variés. Ils ont pour cela accumulé un grand nombre de photos au ratio

, ce qui signifie que le rapport

vaut exactement

. Les photomosaïques mesureront chacune deux mètres de large et seront constituées de

vignettes, toutes de même taille et au même ratio

. Pour garder une bonne qualité d'impression, ils choisissent une résolution de 10 pixels par millimètre.
Q 7. Quelle taille de vignette (

, en pixels) faut-il choisir ? Quelle sera alors la taille en pixels de la photomosaïque?

II.B - Algorithme d'interpolation au plus proche voisin

Cette interpolation est définie par la formule

où

désigne la partie entière de

.
Q 8. Écrire une fonction d'entête
def procheVoisin(A:image, w:int, h:int) -> image:
qui renvoie une nouvelle image correspondant au redimensionnement de l'image

à la taille

en utilisant l'interpolation au plus proche voisin.
Q 9. Quelle est sa complexité temporelle asymptotique ?

II.C - Algorithme de réduction par moyenne locale

On suppose ici que les dimensions de l'image a divisent celles de l'image A:

sont entiers. Afin d'améliorer la qualité de la réduction, on propose la fonction moyenneLocale.

def moyenneLocale(A:image, w:int, h:int) -> image:
    a = np.empty((h, w), np.uint8)
    H, W = A.shape
    ph, pw = H // h, W // w
    for I in range(0, H, ph):
        for J in range(0, W, pw):
            a[I // ph, J // pw] = round(np.mean(A[I:I+ph, J:J+pw]))
    return a

Q 10. Expliquer en quelques lignes son principe de fonctionnement.
Q 11. Donner sa complexité temporelle asymptotique.

II.D - Optimisation de la réduction par moyenne locale

Afin d'accélérer le calcul de la moyenne locale, on précalcule pour chaque image sa table de sommation. La table de sommation d'une image A de

pixels, représentée par le tableau

lignes et

colonnes, est le tableau S à

lignes et

colonnes, défini par

la somme étant prise nulle quand elle ne comporte aucun terme.
Q 12. Le type np.uint32 (entier non signé codé sur 32 bits) est-il suffisant pour stocker les éléments de

si l'image A comporte 50 millions de pixels ? Justifier.
Q 13. Écrire une fonction, de complexité temporelle asymptotique

, d'entête

def tableSommation(A:image) -> np.ndarray:

qui calcule la table de sommation de l'image A.
On suppose à nouveau que les dimensions de l'image A divisent celles de l'image a:

sont entiers. On propose alors la fonction réductionSommation1, qui prend en paramètre l'image A et sa table de sommation

tableSommation

, ainsi que les dimensions de l'image que l'on souhaite obtenir.

def réductionSommation1(A:image, S:np.ndarray, w:int, h:int) -> image:
    a = np.empty((h, w), np.uint8)
    H, W = A.shape
    ph, pw = H // h, W // w
    nbp = ph * pw
    for I in range(0, H, ph):
        for J in range(0, W, pw):
            X = (S[I+ph, J+pw] - S[I+ph, J]) - (S[I, J+pw] - S[I, J])
            a[I // ph, J // pw] = round(X / nbp)
    return a

Q 14. Expliquer en quelques lignes le principe de fonctionnement de réductionSommation1.
Q 15. Donner sa complexité temporelle asymptotique.
Q 16. Montrer que la fonction réductionSommation2 dont le code est fourni ci-dessous donne le même résultat que réductionSommation1.

def réductionSommation2(A:image, S:np.ndarray, w:int, h:int) -> image:
    H, W = A.shape
    ph, pw = H // h, W // w
    sred = S[0:H+1:ph, 0:W+1:pw]
    dc = sred[:, 1:] - sred[:, :-1]
    dl = dc[1:, :] - dc[:-1, :]
    d = dl / (ph * pw)
    return np.uint8(d.round())

Q 17. Comparer les complexités asymptotiques en temps et en mémoire des deux versions de la fonction réductionSommation. Quel est l'avantage de la seconde version?

II.E - Synthèse

Q 18. Discuter des cas d'usage respectifs de procheVoisin, moyenneLocale et réductionSommation pour redimensionner une image.

III Sélection des images de la banque

Une première étape dans la conception d'une photomosaïque est le choix d'une image source et de vignettes. Cette partie est consacrée à la sélection d'images dans la banque.
Les images de la banque sont répertoriées dans une base de données dont le modèle physique est présenté figure 4, dans laquelle les clés primaires sont notées en italique.

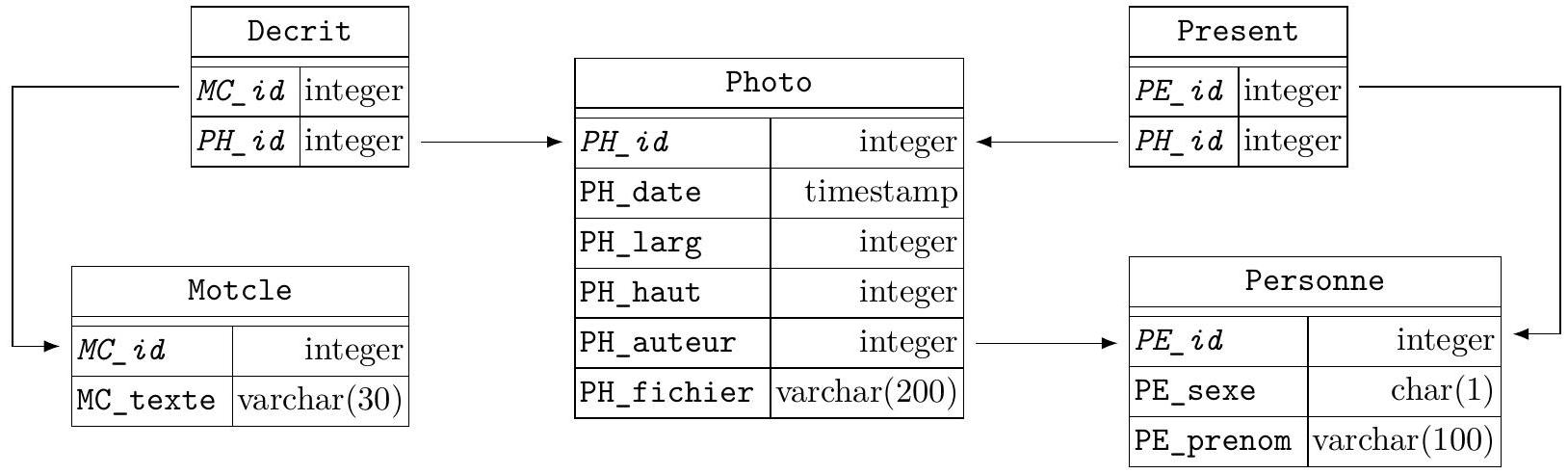
Figure 4 Structure physique de la base de données de photographies.

Cette base comporte les cinq tables listées ci-dessous avec la description de leurs colonnes:

la table Photo répertorie les photographies
PH_id identifiant (entier arbitraire) de la photographie (clé primaire)
PH_date date et heure de la prise de vue
PH_larg, PH_haut largeur et hauteur de la photographie en pixels
PH_auteur identifiant de l'auteur de la photographie
PH_fichier nom du fichier contenant la photographie
la table Personne des modèles et des photographes
PE_id identifiant (entier arbitraire) de la personne (clé primaire)
PE_sexe sexe de la personne ('M' ou 'F')
PE_prenom prénom de la personne
la table Motcle des mots-clés utilisés pour décrire une photographie
MC_id identifiant (entier arbitraire) du mot-clé (clé primaire)
MC_texte le mot-clé lui-même
la table Decrit fait le lien entre les photographies et les mots-clés qui les décrivent, ses deux colonnes constituent sa clé primaire
MC_id identifiant du mot-clé (décrivant la photographie)
PH_id identifiant de la photographie (décrite par le mot-clé)
la table Present fait le lien entre les photographies et les personnes qui y figurent, ses deux colonnes constituent sa clé primaire
PE_id identifiant de la personne (figurant sur la photographie)
PH_id identifiant de la photographie (représentant la personne)

III.A - Quelques requêtes

Pour réaliser les photomosaïques du mariage d'Alice et Bernard, on dispose de plus de 20000 photographies répertoriées dans une base de données dont le modèle est celui de la figure 4 .
Q 19. Écrire une requête SQL donnant les identifiants de toutes les photographies au ratio 4:3, c'est-à-dire dont le rapport largeur sur hauteur vaut exactement

.
Q 20. Écrire une requête qui compte le nombre de photos prises par «Alice» ou «Bernard».
Q 21. Écrire une requête qui fournit l'identifiant et la date des photographies prises avant 2006 et associées au mot-clé «surf ».
Q 22. Écrire une requête qui donne le prénom de l'auteur et l'identifiant de tous les selfies, c'est-à-dire les photographies sur lesquelles l'auteur est présent.
Q 23. Écrire une requête qui sélectionne toutes les photographies sur lesquelles sont présents «Alice» et «Bernard», à l'exclusion de toute autre personne.

III.B - Internationalisation des mots-clés

Afin de partager et d'enrichir la banque d'images, il a été décidé de faire évoluer la structure de la base de données afin de gérer les mots-clés dans différentes langues. Le cahier des charges de cette évolution stipule :
a. l'ensemble des photographies sélectionnées à l'aide de mots-clés ne doit pas dépendre de la langue utilisée pour exprimer ces mots-clés ; autrement dit, les photographies décrites par le mot-clé « montagne » exprimé en français doivent être les mêmes que celles sélectionnées par les mots-clés «mountain » si la langue choisie est l'anglais, «Berg » pour l'allemand, «montaña » pour l'espagnol, etc.;
b. il doit être possible, pour cette nouvelle base de données, d'écrire une requête de recherche de photographies par mot-clef en spécifiant la langue utilisée pour exprimer le mot-clé de telle sorte que changer de langue se fasse en modifiant uniquement des constantes dans la clause WHERE.
Q 24. Proposer un nouveau modèle de base de données répondant à cette évolution du cahier des charges en ne détaillant que ce qui change (tables modifiées, nouvelles tables).
Q 25. Avec cette nouvelle base de données, écrire une requête qui permet de sélectionner les identifiants des photographies associées au mot-clé «mountain » exprimé en anglais.

IV Placement des vignettes

IV.A - Préparatifs

On envisage ici le cas où la photomosaïque est homothétique de l'image source et constituée de

vignettes de haut sur

vignettes de large. Le nombre total de vignettes est donc

.
Q 26. Écrire une fonction d'entête
def initMosaïque(source:image, w:int, h:int, p:int) -> image:
qui prend en paramètre l'image source, les dimensions

d'une vignette et le nombre

de vignettes par coté. Cette fonction renvoie une version redimensionnée de source, de même taille que la photomosaïque finale. On rappelle qu'il est possible d'utiliser les fonctions définies précédemment.

On appelle désormais pavé chaque zone de cette image source redimensionnée, de taille

, qui doit être remplacé par une vignette. Afin de comparer les vignettes et les pavés, on définit la distance

entre deux images

de même taille

par :

Q 27. Écrire une fonction d'entête
def L1(a:image, b:image) -> int:
qui calcule la distance

entre deux images de même taille, en prenant garde aux dépassements de capacité.
Q 28. Écrire une fonction d'entête
def choixVignette(pavé:image, vignettes:[image]) -> int:
qui prend en paramètre une image correspondant à un pavé et une liste de vignettes et qui renvoie l'indice i tel que L1 (pavé, vignettes[i]) est minimal (ou l'un d'entre eux si plusieurs vignettes conviennent). Cette fonction ne doit pas modifier la liste des vignettes.

IV.B - Méthode sans restriction du choix des vignettes

Q 29. Écrire, à l'aide de ce qui précède, une fonction d'entête
def construireMosaïque(source:image, vignettes:[image], p:int) -> image:
qui construit une photomosaïque homothétique de source comportant p vignettes par côté.
Q 30. Déterminer sa complexité temporelle asymptotique en fonction de la taille

des vignettes, du nombre

de vignettes dans la mosaïque et de la longueur

de la liste vignettes.

IV.C - Améliorations

Cette sous-partie demande de l'initiative de la part du candidat, qui peut être amené à définir de nouvelles variables, structures de données et fonctions. Il est demandé d'expliciter clairement la démarche utilisée, de préciser le rôle de chaque nouvelle fonction et variable introduite et de les illustrer, le cas échéant, par un schéma. Toute démarche pertinente, même non aboutie, sera valorisée. Le barème prend en compte le temps nécessaire à la résolution de cette sous-partie.
La méthode sans restriction proposée précédemment peut conduire à sélectionner répétitivement les mêmes vignettes et à mal les répartir. En particulier, une plage uniforme de l'image source conduit à l'accumulation de la même vignette dans cette zone de la photomosaïque.

Q 31. Proposer une stratégie de construction de photomosaïque permettant de sélectionner un maximum de vignettes différentes et, au cas où une vignette serait réutilisée, d'éviter que les différentes apparitions de la même vignette se retrouvent trop proches.
Q 32. Implanter cette stratégie sous la forme d'une fonction belleMosaïque, version améliorée de la fonction construireMosaïque, dont on définira les éventuels paramètres supplémentaires.

Opérations et fonctions disponibles en Python et SQL

Fonctions Python diverses

range(n) itérateur sur les n premiers entiers ( ).
list(range(5)) .
range( ) où et p sont des entiers, itérateur sur les entiers si et si . Le paramètre p est optionnel avec une valeur par défaut de 1.
list (range ; list (range ) .
où est une séquence et et sont des entiers, désigne la séquence des éléments de dont les indices correspondent à range( ). Si est d'un type de base (liste ou tuple), effectue une copie, si est un tableau numpy, est une vue sur les éléments de et peut être utilisé pour modifier s .
.
random. randrange ( a , b ) renvoie un entier aléatoire compris entre a et inclus ( a et b entiers).
random.random() renvoie un nombre flottant tiré aléatoirement dans [ 0,1 [ suivant une distribution uniforme.
random.choice(s) renvoie un élément pris au hasard dans la séquence non vide .
random.shuffle(L) permute aléatoirement les éléments de la liste L (modifie L).
random.sample(s, n) renvoie une liste constituée de n éléments distincts de la séquence choisis aléatoirement, si len(s) lève l'exception ValueError.
math.sqrt(x) calcule la racine carrée du nombre .
round(n) arrondit le nombre n à l'entier le plus proche. Le résultat est de type int pour les types numériques de base. Pour les types de la bibliothèque numpy, le résultat a le même type que l'argument.
math.floor(x) renvoie le plus grand entier inférieur ou égal à .
math.ceil(x) renvoie le plus petit entier supérieur ou égal à .

Opérations sur les listes

len(L) donne le nombre d'éléments de la liste .
L1 + L2 construit une liste constituée de la concaténation des listes L1 et L2.
construit une liste constituée de la liste L concaténée n fois avec elle-même.
in et not in déterminent si l'objet e figure dans la liste . Cette opération a une complexité temporelle en .
2 in True ; 2 not in False.
L. append(e) ajoute l'élément e à la fin de la liste .
L.pop(i) : renvoie l'élément à l'indice i de la liste L et le supprime de la liste.
L.remove(e) supprime de la liste L le premier élément qui a pour valeur e, s'il existe. Cette opération a une complexité temporelle en .
L.insert(i, e) insère l'élément e à la position d'indice i dans la liste L (en décalant les éléments suivants); si i len(L), e est ajouté en fin de liste.
L.sort() trie en place la liste L (qui est donc modifiée) en réordonnant ses éléments dans l'ordre croissant.

Opérations sur les tableaux (np.ndarray)

np.array(s, dtype) crée un nouveau tableau contenant les éléments de la séquence . La taille de ce tableau est déduite du contenu de . Le paramètre dtype précise le type des éléments du tableau créé.
np.empty( , dtype), np.empty( ), dtype) crée respectivement un tableau à une dimension de éléments et un tableau à lignes et colonnes dont les éléments, de valeurs indéterminées, sont de type dtype. Si le paramètre dtype n'est pas précisé, il prend la valeur float.
np.zeros(n, dtype), np.zeros((n, m), dtype) fonctionne comme np.empty en initialisant chaque élément à la valeur zéro pour les types numériques ou False pour les types booléens.
np.full(n, v, dtype), np.full((n, m), v, dtype) fonctionne comme np.empty en initialisant chaque élément à la valeur v .
a.ndim nombre de dimensions du tableau a.
a.shape tuple donnant la taille du tableau a pour chacune de ses dimensions.
len(a) taille du tableau a dans sa première dimension, équivalent à a.shape[0].
a.size nombre total d'éléments du tableau a.
a.dtype type des éléments du tableau a.
a.flat itérateur sur tous les éléments du tableau a.
np.ndenumerate(a) itérateur sur tous les couples (ind, v) du tableau a où ind est un tuple de a.ndim entiers donnant les indices de l'élément .
a.min(), a.max() renvoie la valeur du plus petit (respectivement plus grand) élément du tableau a; ces opérations ont une complexité temporelle en (a.size).
a.sum() ou np.sum(a) calcule la somme de tous les éléments du tableau a; cette opération a une complexité temporelle en (a.size).
a.sum(d) ou np.sum(a, d) effectue la somme des éléments du tableau a suivant la dimension d; le résultat est un nouveau tableau avec une dimension de moins que a.
a.sum(0) somme par ligne, a.sum(1) somme par colonne, etc.
a.mean() ou np.mean(a) renvoie la valeur moyenne de tous les éléments du tableau a; le résultat est de type np.float64. Cette opération a une complexité temporelle en (a.size).
a.mean(d) ou np.mean(a, d) effectue la moyenne des éléments du tableau a suivant la dimension d; le résultat est un nouveau tableau avec une dimension de moins que a.
a.mean moyenne par ligne, a.mean moyenne par colonne, etc.
a.round(), np.around(a) crée un nouveau tableau de même forme et type que a en arrondissant ses éléments à l'entier le plus proche.

T1 JOIN T2 USING (c1, c2, ...) joint les deux tables T1 et T2 sur les colonnes c1, c2... qui doivent exister dans les deux tables; équivalent à AND AND , sauf que les colonnes c1, c2... n'apparaissent qu'une fois dans le résultat.
Les requêtes
(SELECT ... FROM ... WHERE ...) INTERSECT (SELECT ... FROM ... WHERE ...)
(SELECT ... FROM ... WHERE ...) UNION (SELECT ... FROM ... WHERE ...)
(SELECT ... FROM ... WHERE ...) EXCEPT (SELECT ... FROM ... WHERE ...)
sélectionnent respectivement l'intersection, l'union et la différence des résultats des deux requêtes, qui doivent être compatibles : même nombre de colonnes et mêmes types.
EXTRACT (part FROM t ) extrait un élément de t , expression de type date, time, timestamp (jour et heure) ou interval (durée). part peut prendre les valeurs year, month, day (jour dans le mois), doy (jour dans l'année), dow (jour de la semaine), hour, etc.
Les fonctions d'agrégation calculent respectivement la somme, la moyenne arithmétique, le maximum, le minium, le nombre de valeurs non nulles de l'expression e et le nombre de lignes pour chaque groupe de lignes défini par la cause GROUP BY. Si la requête ne comporte pas de clause GROUP BY le calcul est effectué pour l'ensemble des lignes sélectionnées par la requête.

Photo par «Sincerely Media», issue de https://unsplash.com.
Vignettes issues de la banque https://picsum.photos/images.